【课件】1.1.1 集合及其表示方法 高中数学-RJB-必修第一册-第一章(共28张PPT)
文档属性
| 名称 | 【课件】1.1.1 集合及其表示方法 高中数学-RJB-必修第一册-第一章(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
数学-RJB-必修第一册
1.1.1 集合及其表示方法
第一章 集合与常用逻辑用语
重点:集合的含义与表示方法,常用数集的符号表示.
难点:对集合的特征性质的理解及运用特征性质描述法表示集合.
1.通过实例,了解集合的含义,体会元素与集合的“属于”关系.
2.掌握集合中元素的特性.
3.能选择列举法或描述法表示不同的集合,感受集合语言的意义和作用.
4.掌握集合的分类与几种常见数集的表示方法.
5.理解区间的概念及其表示方法.
学习目标
知识梳理
一、集合与元素的含义
在数学中,我们经常用“集合”来对所研究的对象进行分类.
◆把一些能够确定的、不同的对象汇集在一起,就说由这些对象组成一个集合(有时简称为集),
◆组成集合的每个对象都是这个集合的元素.
二、集合的字母表示
◆集合通常用英文大写字母A,B,C,…表示,
◆集合的元素通常用英文小写字母a,b,c,…表示.
三、元素与集合的关系及记法
◆如果a是集合A的元素,就记作aA,读作“a属于A”;
◆如果a不是集合A的元素,就记作aA,读作“a不属于A”.
一般地,我们把不含任何元素的集合称为空集,记作
四、集合的相等
给定两个集合A和B,如果组成它们的元素完全相同,就称这两个集合相等,记作A=B.
五、集合的分类
集合可以根据它含有的元素个数分为两类:
◆含有有限个元素的集合称为有限集,
◆含有无限个元素的集合称为无限集.
空集可以看成包含0个元素的集合,所以空集是有限集.
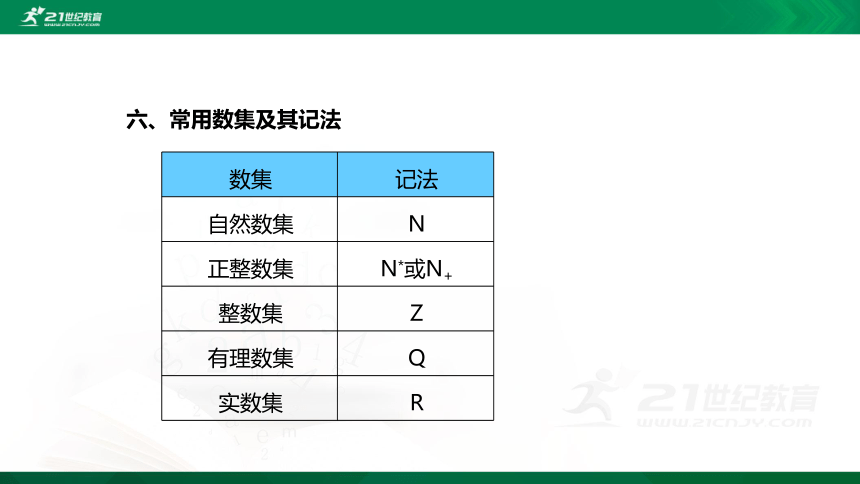
六、常用数集及其记法
数集 记法
自然数集 N
正整数集 N*或N+
整数集 Z
有理数集 Q
实数集 R
七、集合的表示方法
◆把集合中的元素一一列举出来(相邻元素之间用逗号分隔),并写在大括号内,以此来表示集合的方法称为列举法.
①由两个元素0,1组成的集合可用列举法表示为
{0,1};
②24的所有正因数1,2,3,4,6,8,12,24组成的集合可用列举法表示为
{1,2,3,4,6,8,12,24};
③中国古典长篇小说四大名著组成的集合可以表示为
{《红楼梦》,《三国演义》,《水浒传》,《西游记》}.
例
一般地,如果属于集合A的任意一个元素x都具有性质p(x),而不属于集合A的元素都不具有这个性质,则性质p(x)称为集合A的一个特征性质.此时,
◆集合A可以用它的特征性质p(x)表示为{x|p(x)}.这种表示集合的方法,称为特征性质描述法,简称为描述法.
①“一组对边平行且相等的四边形”是平行四边形的一个特征性质,因此所有平行四边形组成的集合可以表示为
{x|x是一组对边平行且相等的四边形}.
②所有能被3整除的整数组成的集合,可以用描述法表示为
{x|x=3n,n∈Z}.
例
八、区间及其表示
设a,b∈R,且a[a,b]={x|a≤x≤b},
(a,b)={x|a[a,b)={x|a≤x(a,b]={x|a(a,+∞)={x|x>a},
(-∞,b)={x|x(-∞,+∞)=R .
[a,b],(a,b)分别叫做闭区间、开区间;[a,b),(a,b]叫做半开半闭区间;a,b叫做相应区间的端点.
常考题型
√
变式训练
1-1
√
判断一组对象是否能组成集合的依据
判断一组对象是否能组成集合,要看这组对象是否满足集合元素的“确定性”,即能否找到一个明确的标准,使得对于任何一个对象,都能确定它是不是给定集合的元素.如果有明确的标准,就可以组成集合;否则,不能组成集合.
解题归纳
如何选择适当的方法表示集合?
一个集合可以用不同的表示方法表示,所谓适当的表示方法,就是比较简单明了的表示方法,其中列举法和描述法是表示集合的常用方法.
◆列举法通常用于表示元素个数较少的集合,
◆描述法通常用于表示元素具有明显共同特征的集合.
解题归纳
√
利用集合相等的定义,判断集合是否相等的方法
1.若集合是列举法给出的,则直接对比看这几个集合所含元素是否相同.若相同则两个集合相等;
2.若集合是描述法给出的,则判断这几个集合所含元素相同要依次满足两点:
(1)两个集合的代表元素相同;(2)所有元素的共同性质相同,包括元素的范围相同.若上述两点均相同,则两个集合相等.
解题归纳
1
变式训练
5-1
已知含参集合和元素,在元素与集合关系限制条件下,求参数的方法
1.当a∈A时,若集合A是用列举法表示的,则a一定等于集合A中的某个元素.
若集合A是用描述法表示的,则a一定满足集合A中元素的共同特征,如满足方程(组)、不等式(组)等.
2.若aA时,则结论相反.
利用上述结论建立方程(组)或不等式(组)求解参数即可 .
解题归纳
变式训练
5-2
小结
两个知识点:
1.集合与元素的含义;2.集合的字母表示;3.元素与集合的关系及记法;4.集合的相等;5. 集合的分类;6.常用数集及其记法;7.集合的表示方法;8.区间及其表示.
五种题型:
1.判断某些对象的全体是否组成集合;
2.用适当的方法表示集合;
3.已知集合的描述法表示,求元素个数;
4.判断集合是否相等;
5.已知含参集合或元素,求参问题.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJB-必修第一册
1.1.1 集合及其表示方法
第一章 集合与常用逻辑用语
重点:集合的含义与表示方法,常用数集的符号表示.
难点:对集合的特征性质的理解及运用特征性质描述法表示集合.
1.通过实例,了解集合的含义,体会元素与集合的“属于”关系.
2.掌握集合中元素的特性.
3.能选择列举法或描述法表示不同的集合,感受集合语言的意义和作用.
4.掌握集合的分类与几种常见数集的表示方法.
5.理解区间的概念及其表示方法.
学习目标
知识梳理
一、集合与元素的含义
在数学中,我们经常用“集合”来对所研究的对象进行分类.
◆把一些能够确定的、不同的对象汇集在一起,就说由这些对象组成一个集合(有时简称为集),
◆组成集合的每个对象都是这个集合的元素.
二、集合的字母表示
◆集合通常用英文大写字母A,B,C,…表示,
◆集合的元素通常用英文小写字母a,b,c,…表示.
三、元素与集合的关系及记法
◆如果a是集合A的元素,就记作aA,读作“a属于A”;
◆如果a不是集合A的元素,就记作aA,读作“a不属于A”.
一般地,我们把不含任何元素的集合称为空集,记作
四、集合的相等
给定两个集合A和B,如果组成它们的元素完全相同,就称这两个集合相等,记作A=B.
五、集合的分类
集合可以根据它含有的元素个数分为两类:
◆含有有限个元素的集合称为有限集,
◆含有无限个元素的集合称为无限集.
空集可以看成包含0个元素的集合,所以空集是有限集.
六、常用数集及其记法
数集 记法
自然数集 N
正整数集 N*或N+
整数集 Z
有理数集 Q
实数集 R
七、集合的表示方法
◆把集合中的元素一一列举出来(相邻元素之间用逗号分隔),并写在大括号内,以此来表示集合的方法称为列举法.
①由两个元素0,1组成的集合可用列举法表示为
{0,1};
②24的所有正因数1,2,3,4,6,8,12,24组成的集合可用列举法表示为
{1,2,3,4,6,8,12,24};
③中国古典长篇小说四大名著组成的集合可以表示为
{《红楼梦》,《三国演义》,《水浒传》,《西游记》}.
例
一般地,如果属于集合A的任意一个元素x都具有性质p(x),而不属于集合A的元素都不具有这个性质,则性质p(x)称为集合A的一个特征性质.此时,
◆集合A可以用它的特征性质p(x)表示为{x|p(x)}.这种表示集合的方法,称为特征性质描述法,简称为描述法.
①“一组对边平行且相等的四边形”是平行四边形的一个特征性质,因此所有平行四边形组成的集合可以表示为
{x|x是一组对边平行且相等的四边形}.
②所有能被3整除的整数组成的集合,可以用描述法表示为
{x|x=3n,n∈Z}.
例
八、区间及其表示
设a,b∈R,且a
(a,b)={x|a
(-∞,b)={x|x
[a,b],(a,b)分别叫做闭区间、开区间;[a,b),(a,b]叫做半开半闭区间;a,b叫做相应区间的端点.
常考题型
√
变式训练
1-1
√
判断一组对象是否能组成集合的依据
判断一组对象是否能组成集合,要看这组对象是否满足集合元素的“确定性”,即能否找到一个明确的标准,使得对于任何一个对象,都能确定它是不是给定集合的元素.如果有明确的标准,就可以组成集合;否则,不能组成集合.
解题归纳
如何选择适当的方法表示集合?
一个集合可以用不同的表示方法表示,所谓适当的表示方法,就是比较简单明了的表示方法,其中列举法和描述法是表示集合的常用方法.
◆列举法通常用于表示元素个数较少的集合,
◆描述法通常用于表示元素具有明显共同特征的集合.
解题归纳
√
利用集合相等的定义,判断集合是否相等的方法
1.若集合是列举法给出的,则直接对比看这几个集合所含元素是否相同.若相同则两个集合相等;
2.若集合是描述法给出的,则判断这几个集合所含元素相同要依次满足两点:
(1)两个集合的代表元素相同;(2)所有元素的共同性质相同,包括元素的范围相同.若上述两点均相同,则两个集合相等.
解题归纳
1
变式训练
5-1
已知含参集合和元素,在元素与集合关系限制条件下,求参数的方法
1.当a∈A时,若集合A是用列举法表示的,则a一定等于集合A中的某个元素.
若集合A是用描述法表示的,则a一定满足集合A中元素的共同特征,如满足方程(组)、不等式(组)等.
2.若aA时,则结论相反.
利用上述结论建立方程(组)或不等式(组)求解参数即可 .
解题归纳
变式训练
5-2
小结
两个知识点:
1.集合与元素的含义;2.集合的字母表示;3.元素与集合的关系及记法;4.集合的相等;5. 集合的分类;6.常用数集及其记法;7.集合的表示方法;8.区间及其表示.
五种题型:
1.判断某些对象的全体是否组成集合;
2.用适当的方法表示集合;
3.已知集合的描述法表示,求元素个数;
4.判断集合是否相等;
5.已知含参集合或元素,求参问题.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
