2.4.1平面向量的数量积
图片预览







文档简介
课件24张PPT。2.4.1平面向量的数量积学习目标:(1)理解和掌握向量数量积的定义;
(2)理解向量数量积的几何意义;
(3)掌握向量数量积的运算律;
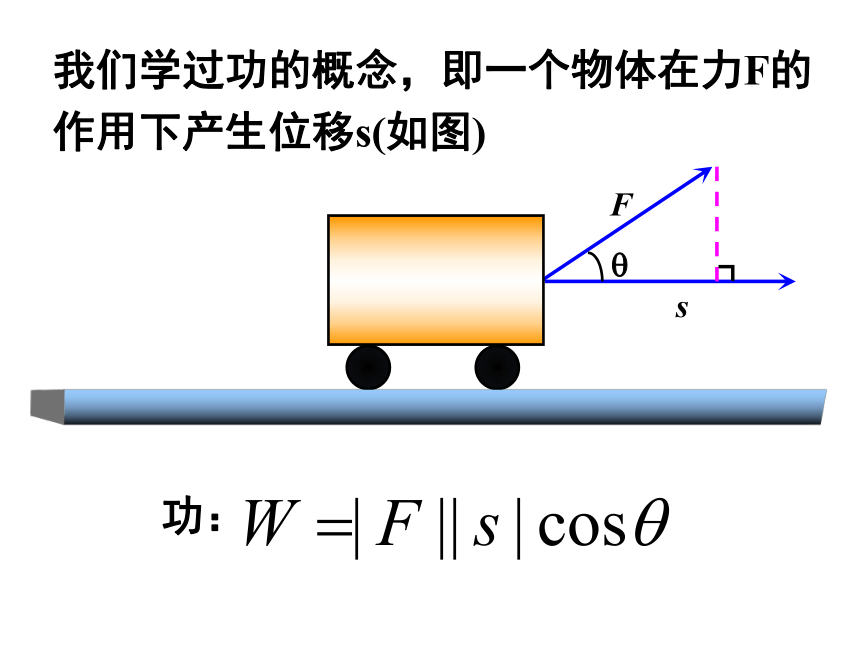
(4)掌握向量数量积的重要性质.功:我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)一、平面向量数量积的定义:已知两个非零向量 和 ,它们的夹角为? ,
我们把数量 叫做 与 的数量积
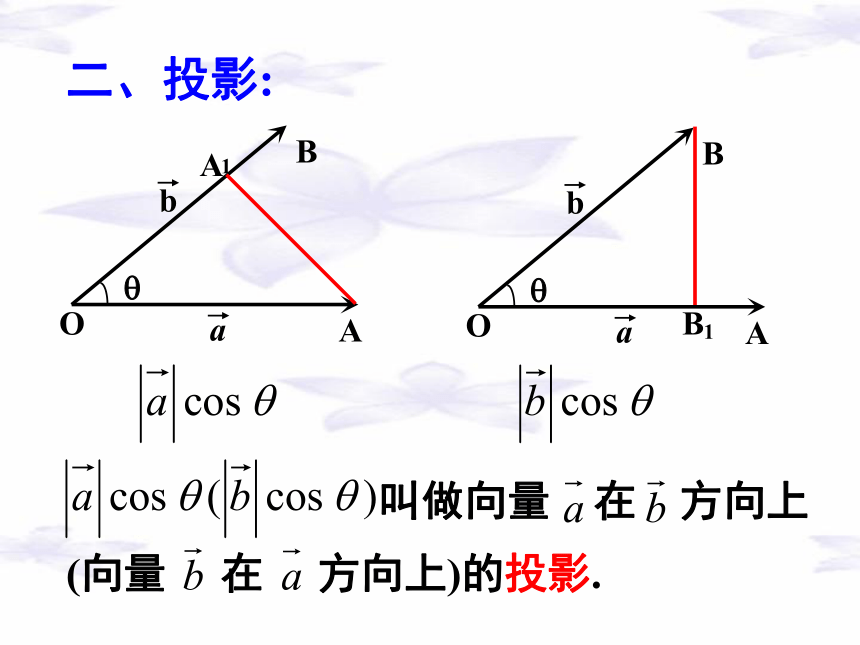
(或内积),记作 .规定:零向量与任意向量的数量积为0.注意:3、若 不能得出 或 向量的数量积是一个数量,那么它什么时候为正,什么时候为负?探究:当0°≤θ<90°时 > 0当θ =90°时 = 0当90°<θ≤180°时 < 0解:二、投影: 叫做向量 在 方向上(向量 在 方向上)的投影. 向量 在方向 上的投影是数量,不是向量,什么时候为正,什么时候为负?探究:三、平面向量数量积的几何意义:四、平面向量数量积的运算律:(1)交换律:(2)数乘结合律: (3)分配律: 数量积不满足下面的运算注意:结论:五、平面向量数量积的重要性质:判断两个向量垂直的依据求向量模的依据求向量夹角的依据五、平面向量数量积的重要性质:练习:判断下列各题是否正确:(1)若a=0,则对任意向量b,有a·b=0
(2)若a≠0,则对任意非零向量b,有a·b≠0
(3)若a≠0,且a·b=0,则b=0
(4)若a·b=0,则a=0或b=0
(5)对任意向量a,有a2=│a│2
(6)若a≠0且a·b=a·c,则b=c√××××√一、利用向量的垂直解题:例1:例2:二、利用 求模:解:例3:三、利用 求夹角:例3:三、利用 求夹角:解:【总一总★成竹在胸】公式变形对功W=|F||s|cos?结构分析抽
象特殊化重要性质数形结合几何
意义
(2)理解向量数量积的几何意义;
(3)掌握向量数量积的运算律;
(4)掌握向量数量积的重要性质.功:我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)一、平面向量数量积的定义:已知两个非零向量 和 ,它们的夹角为? ,
我们把数量 叫做 与 的数量积
(或内积),记作 .规定:零向量与任意向量的数量积为0.注意:3、若 不能得出 或 向量的数量积是一个数量,那么它什么时候为正,什么时候为负?探究:当0°≤θ<90°时 > 0当θ =90°时 = 0当90°<θ≤180°时 < 0解:二、投影: 叫做向量 在 方向上(向量 在 方向上)的投影. 向量 在方向 上的投影是数量,不是向量,什么时候为正,什么时候为负?探究:三、平面向量数量积的几何意义:四、平面向量数量积的运算律:(1)交换律:(2)数乘结合律: (3)分配律: 数量积不满足下面的运算注意:结论:五、平面向量数量积的重要性质:判断两个向量垂直的依据求向量模的依据求向量夹角的依据五、平面向量数量积的重要性质:练习:判断下列各题是否正确:(1)若a=0,则对任意向量b,有a·b=0
(2)若a≠0,则对任意非零向量b,有a·b≠0
(3)若a≠0,且a·b=0,则b=0
(4)若a·b=0,则a=0或b=0
(5)对任意向量a,有a2=│a│2
(6)若a≠0且a·b=a·c,则b=c√××××√一、利用向量的垂直解题:例1:例2:二、利用 求模:解:例3:三、利用 求夹角:例3:三、利用 求夹角:解:【总一总★成竹在胸】公式变形对功W=|F||s|cos?结构分析抽
象特殊化重要性质数形结合几何
意义
