人教版数学七年级下册第5章 相交线与平行线 专题一中考重难点 课件(共30张PPT)
文档属性
| 名称 | 人教版数学七年级下册第5章 相交线与平行线 专题一中考重难点 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 650.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 19:50:20 | ||
图片预览




文档简介
(共30张PPT)
单元复习课
专题一 中考重难点
一、平行线的判定
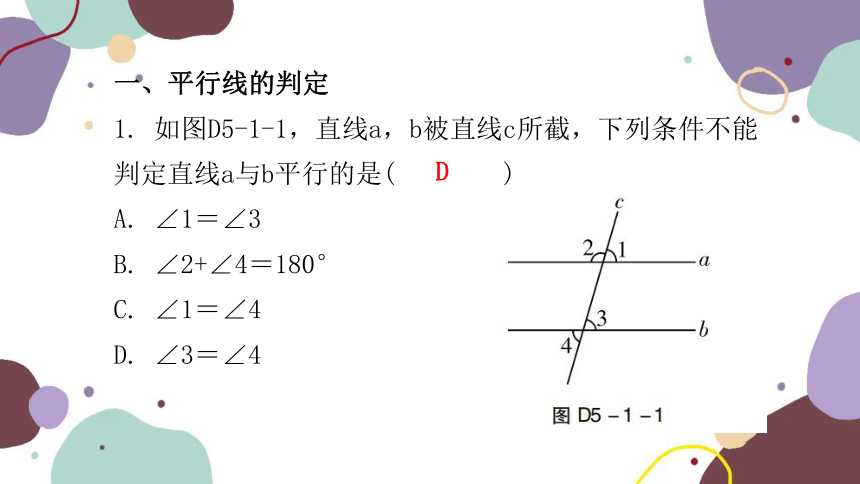
1. 如图D5-1-1,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
A. ∠1=∠3
B. ∠2+∠4=180°
C. ∠1=∠4
D. ∠3=∠4
D
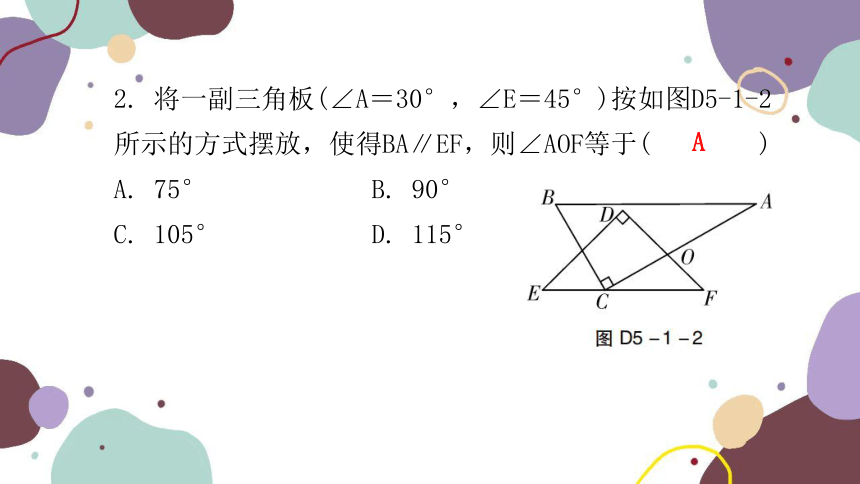
2. 将一副三角板(∠A=30°,∠E=45°)按如图D5-1-2所示的方式摆放,使得BA∥EF,则∠AOF等于( )
A. 75° B. 90°
C. 105° D. 115°
A
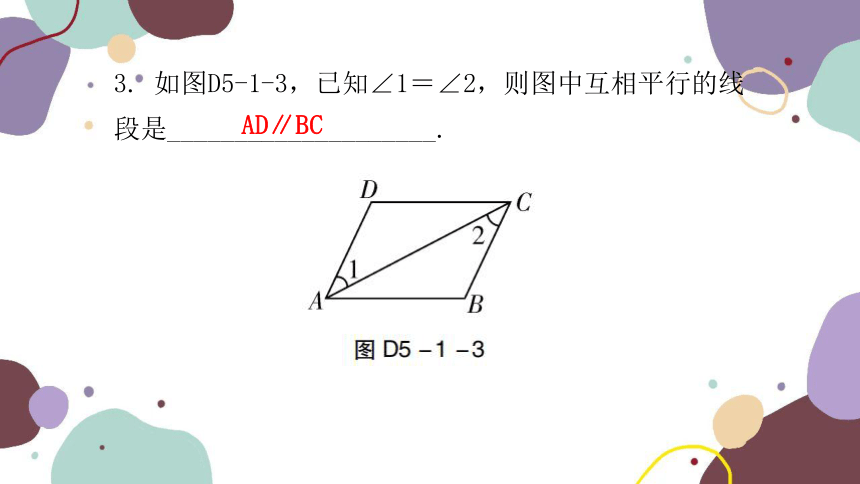
3. 如图D5-1-3,已知∠1=∠2,则图中互相平行的线段是____________________.
AD∥BC
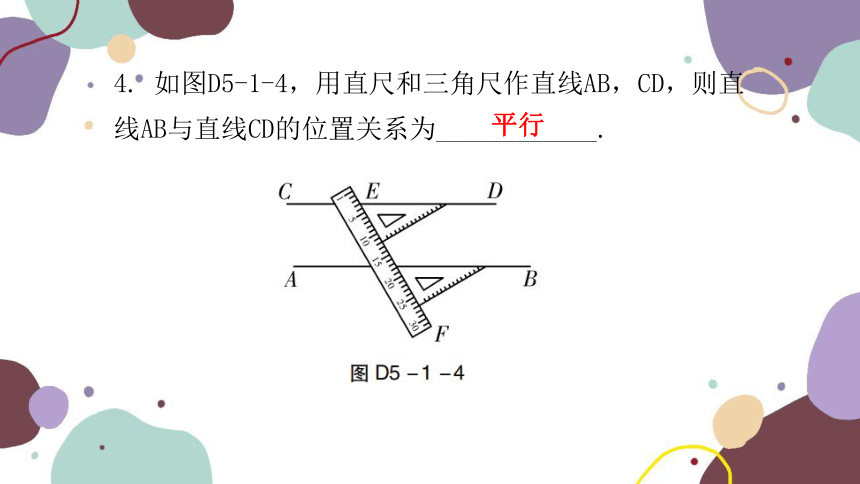
4. 如图D5-1-4,用直尺和三角尺作直线AB,CD,则直线AB与直线CD的位置关系为____________.
平行
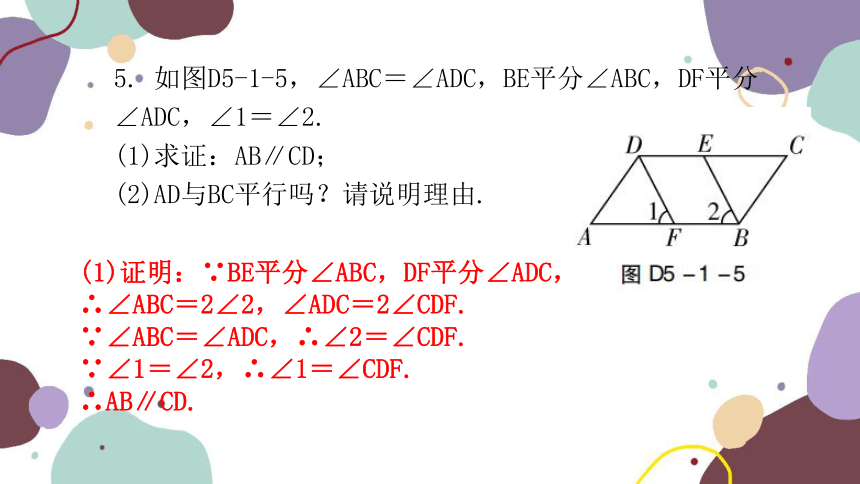
5. 如图D5-1-5,∠ABC=∠ADC,BE平分∠ABC,DF平分∠ADC,∠1=∠2.
(1)求证:AB∥CD;
(2)AD与BC平行吗?请说明理由.
(1)证明:∵BE平分∠ABC,DF平分∠ADC,
∴∠ABC=2∠2,∠ADC=2∠CDF.
∵∠ABC=∠ADC,∴∠2=∠CDF.
∵∠1=∠2,∴∠1=∠CDF.
∴AB∥CD.
(2)解:AD∥BC. 理由如下:
∵AB∥CD,
∴∠ABC+∠C=180°.
∵∠ABC=∠ADC,
∴∠ADC+∠C=180°.
∴AD∥BC.
6. 如图D5-1-6,已知AD∥BE,∠1=∠2,∠3=∠4,求证:AB∥CD.
证明:∵AD∥BE,∴∠3=∠CAD.
∵∠3=∠4,∴∠4=∠CAD.
∵∠1=∠2,∴∠1+∠CAE=∠2+∠CAE,
即∠BAE=∠CAD.
∴∠4=∠BAE.
∴AB∥CD.
7. 如图D5-1-7,DG⊥BC,AC⊥BC,∠1=∠2.求证:EF∥CD.
证明:∵DG⊥BC,AC⊥BC,
∴∠DGB=∠ACB=90°(垂直的定义).
∴DG∥AC(同位角相等,两直线平行).
∴∠2=∠ACD(两直线平行,内错角相等).
∵∠1=∠2,∴∠1=∠ACD.
∴EF∥CD(同位角相等,两直线平行).
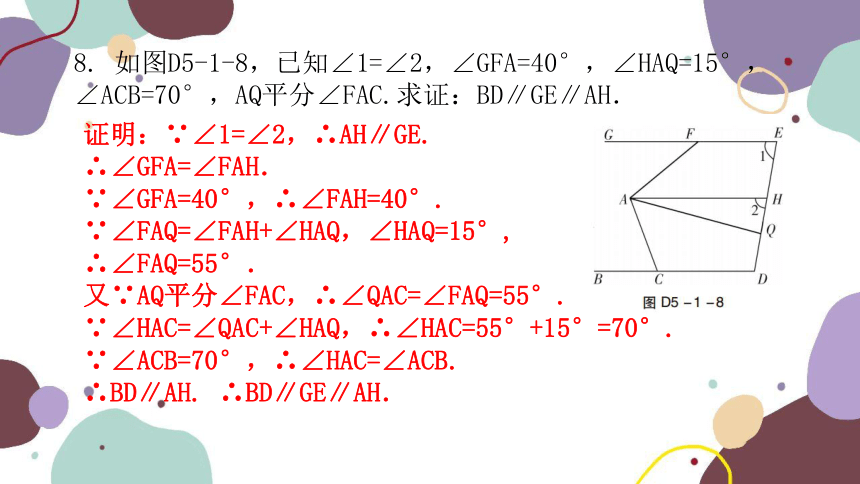
8. 如图D5-1-8,已知∠1=∠2,∠GFA=40°,∠HAQ=15°,∠ACB=70°,AQ平分∠FAC.求证:BD∥GE∥AH.
证明:∵∠1=∠2,∴AH∥GE.
∴∠GFA=∠FAH.
∵∠GFA=40°,∴∠FAH=40°.
∵∠FAQ=∠FAH+∠HAQ,∠HAQ=15°,
∴∠FAQ=55°.
又∵AQ平分∠FAC,∴∠QAC=∠FAQ=55°.
∵∠HAC=∠QAC+∠HAQ,∴∠HAC=55°+15°=70°.
∵∠ACB=70°,∴∠HAC=∠ACB.
∴BD∥AH. ∴BD∥GE∥AH.
【对接中考】
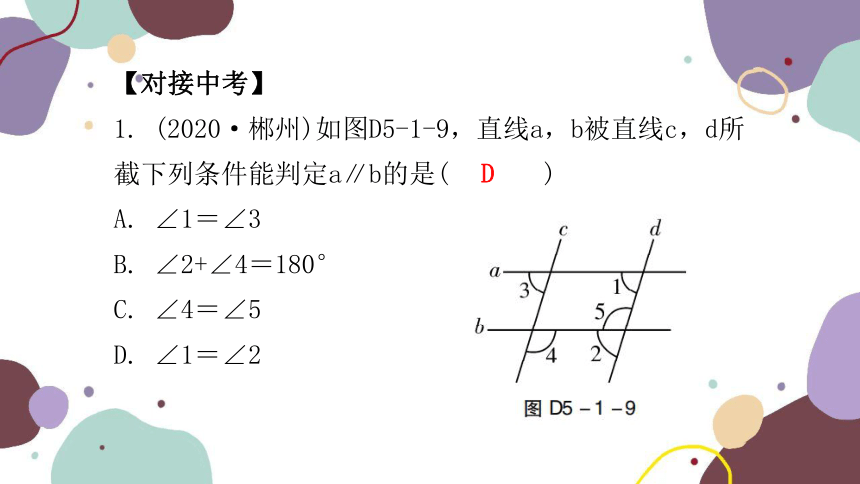
1. (2020·郴州)如图D5-1-9,直线a,b被直线c,d所截下列条件能判定a∥b的是( )
A. ∠1=∠3
B. ∠2+∠4=180°
C. ∠4=∠5
D. ∠1=∠2
D
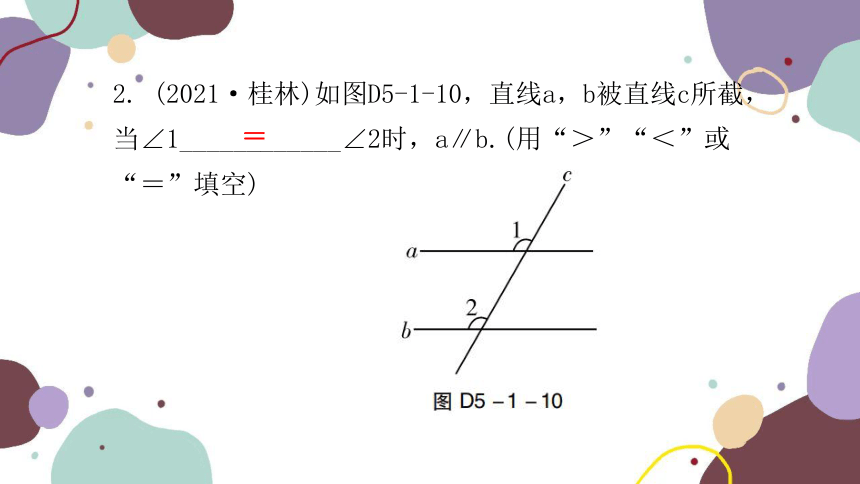
2. (2021·桂林)如图D5-1-10,直线a,b被直线c所截,当∠1____________∠2时,a∥b.(用“>”“<”或“=”填空)
=
3. (2021·泰州)如图D5-1-11,木棒AB,CD与EF分别在G,H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转____________°.
20
4. (2020·咸宁)如图D5-1-12,请填写一个条件,使结论成立:∵__________________________,∴a∥b.
∠1=∠4(答案不唯一)
5. (2021·武汉)如图D5-1-13,AB∥CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F,
求证:∠DEF=∠F.
证明:∵AB∥CD,∴∠DCF=∠B.
∵∠B=∠D,∴∠DCF=∠D.
∴AD∥BC. ∴∠DEF=∠F.
二、平行线的性质
1. 如图D5-1-14,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( )
A. 50°
B. 60°
C. 70°
D. 80°
C
2. 如图D5-1-15,若l1∥l2,l3∥l4,则图中与∠1互补的角有( )
A. 1个 B. 2个 C. 3个 D. 4个
3. 如图D5-1-16,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为____________.
D
132°
4. 如图D5-1-17,AB∥CD,点E,F分别在线段AD,BC上,连接AC交EF于G,∠1=∠BAC. 若∠CAF=15°,∠2=45°,∠3=20°,求∠B和∠ACD的度数.
解:∵∠1=∠BAC,∴AB∥EF.
∴∠B+∠BFE=180°.
∵∠2=45°,∠3=20°,
∴∠BFE=65°,∠B=115°.
∵EF∥AB,∴∠FAB=∠3=20°.
∴∠CAB=∠CAF+∠FAB=15°+20°=35°.
∵AB∥CD,∴∠ACD=∠CAB=35°.
5. 如图D5-1-18,已知AM∥BN,∠A=60°,点P是射线AM上一个动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB ∶∠ADB的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到某处时,∠ACB=∠ABD,求此时∠ABC的度数.
【对接中考】
1. (2021·鞍山)直线a∥b,将一个含30°角的三角尺按如图D5-1-19所示的位置放置,若∠1=24°,则∠2的度数为( )
A. 120° B. 136°
C. 144° D. 156°
C
2. (2021·包头)如图D5-1-20,直线l1∥l2,直线l3交l1于点A,交l2于点B,过点B的直线l4交l1于点C. 若∠3=50°,∠1+∠2+∠3=240°,则∠4等于( )
A. 80° B. 70°
C. 60° D. 50°
B
3. (2021·岳阳)将一副直角三角板按如图D5-1-21所示的方式摆放,若直线a∥b,则∠1的大小为( )
A. 45°
B. 60°
C. 75°
D. 105°
C
4. (2021·达州)如图D5-1-22,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=40°时,∠DCN的度数为( )
A. 40° B. 50°
C. 60° D. 80°
B
5. (2021·贵港)如图D5-1-23,AB∥CD,CB平分∠ECD,若∠B=26°,则∠1的度数是____________.
52°
6. (2021·恩施州)如图D5-1-24,已知AE∥BC,若∠BAC=100°,∠DAE=50°,则∠C=____________.
30°
7. (2021·张家界)如图D5-1-25,已知AB∥CD,BC是∠ABD的平分线,若∠2=64°,则∠3=__________.
58°
8. (2019·武汉)如图D5-1-26,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF,求证:∠E=∠F.
证明:∵∠A=∠1,
∴AE∥BF. ∴∠2=∠E.
∵CE∥DF,∴∠2=∠F.
∴∠E=∠F.
谢 谢
单元复习课
专题一 中考重难点
一、平行线的判定
1. 如图D5-1-1,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
A. ∠1=∠3
B. ∠2+∠4=180°
C. ∠1=∠4
D. ∠3=∠4
D
2. 将一副三角板(∠A=30°,∠E=45°)按如图D5-1-2所示的方式摆放,使得BA∥EF,则∠AOF等于( )
A. 75° B. 90°
C. 105° D. 115°
A
3. 如图D5-1-3,已知∠1=∠2,则图中互相平行的线段是____________________.
AD∥BC
4. 如图D5-1-4,用直尺和三角尺作直线AB,CD,则直线AB与直线CD的位置关系为____________.
平行
5. 如图D5-1-5,∠ABC=∠ADC,BE平分∠ABC,DF平分∠ADC,∠1=∠2.
(1)求证:AB∥CD;
(2)AD与BC平行吗?请说明理由.
(1)证明:∵BE平分∠ABC,DF平分∠ADC,
∴∠ABC=2∠2,∠ADC=2∠CDF.
∵∠ABC=∠ADC,∴∠2=∠CDF.
∵∠1=∠2,∴∠1=∠CDF.
∴AB∥CD.
(2)解:AD∥BC. 理由如下:
∵AB∥CD,
∴∠ABC+∠C=180°.
∵∠ABC=∠ADC,
∴∠ADC+∠C=180°.
∴AD∥BC.
6. 如图D5-1-6,已知AD∥BE,∠1=∠2,∠3=∠4,求证:AB∥CD.
证明:∵AD∥BE,∴∠3=∠CAD.
∵∠3=∠4,∴∠4=∠CAD.
∵∠1=∠2,∴∠1+∠CAE=∠2+∠CAE,
即∠BAE=∠CAD.
∴∠4=∠BAE.
∴AB∥CD.
7. 如图D5-1-7,DG⊥BC,AC⊥BC,∠1=∠2.求证:EF∥CD.
证明:∵DG⊥BC,AC⊥BC,
∴∠DGB=∠ACB=90°(垂直的定义).
∴DG∥AC(同位角相等,两直线平行).
∴∠2=∠ACD(两直线平行,内错角相等).
∵∠1=∠2,∴∠1=∠ACD.
∴EF∥CD(同位角相等,两直线平行).
8. 如图D5-1-8,已知∠1=∠2,∠GFA=40°,∠HAQ=15°,∠ACB=70°,AQ平分∠FAC.求证:BD∥GE∥AH.
证明:∵∠1=∠2,∴AH∥GE.
∴∠GFA=∠FAH.
∵∠GFA=40°,∴∠FAH=40°.
∵∠FAQ=∠FAH+∠HAQ,∠HAQ=15°,
∴∠FAQ=55°.
又∵AQ平分∠FAC,∴∠QAC=∠FAQ=55°.
∵∠HAC=∠QAC+∠HAQ,∴∠HAC=55°+15°=70°.
∵∠ACB=70°,∴∠HAC=∠ACB.
∴BD∥AH. ∴BD∥GE∥AH.
【对接中考】
1. (2020·郴州)如图D5-1-9,直线a,b被直线c,d所截下列条件能判定a∥b的是( )
A. ∠1=∠3
B. ∠2+∠4=180°
C. ∠4=∠5
D. ∠1=∠2
D
2. (2021·桂林)如图D5-1-10,直线a,b被直线c所截,当∠1____________∠2时,a∥b.(用“>”“<”或“=”填空)
=
3. (2021·泰州)如图D5-1-11,木棒AB,CD与EF分别在G,H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转____________°.
20
4. (2020·咸宁)如图D5-1-12,请填写一个条件,使结论成立:∵__________________________,∴a∥b.
∠1=∠4(答案不唯一)
5. (2021·武汉)如图D5-1-13,AB∥CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F,
求证:∠DEF=∠F.
证明:∵AB∥CD,∴∠DCF=∠B.
∵∠B=∠D,∴∠DCF=∠D.
∴AD∥BC. ∴∠DEF=∠F.
二、平行线的性质
1. 如图D5-1-14,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( )
A. 50°
B. 60°
C. 70°
D. 80°
C
2. 如图D5-1-15,若l1∥l2,l3∥l4,则图中与∠1互补的角有( )
A. 1个 B. 2个 C. 3个 D. 4个
3. 如图D5-1-16,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为____________.
D
132°
4. 如图D5-1-17,AB∥CD,点E,F分别在线段AD,BC上,连接AC交EF于G,∠1=∠BAC. 若∠CAF=15°,∠2=45°,∠3=20°,求∠B和∠ACD的度数.
解:∵∠1=∠BAC,∴AB∥EF.
∴∠B+∠BFE=180°.
∵∠2=45°,∠3=20°,
∴∠BFE=65°,∠B=115°.
∵EF∥AB,∴∠FAB=∠3=20°.
∴∠CAB=∠CAF+∠FAB=15°+20°=35°.
∵AB∥CD,∴∠ACD=∠CAB=35°.
5. 如图D5-1-18,已知AM∥BN,∠A=60°,点P是射线AM上一个动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB ∶∠ADB的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到某处时,∠ACB=∠ABD,求此时∠ABC的度数.
【对接中考】
1. (2021·鞍山)直线a∥b,将一个含30°角的三角尺按如图D5-1-19所示的位置放置,若∠1=24°,则∠2的度数为( )
A. 120° B. 136°
C. 144° D. 156°
C
2. (2021·包头)如图D5-1-20,直线l1∥l2,直线l3交l1于点A,交l2于点B,过点B的直线l4交l1于点C. 若∠3=50°,∠1+∠2+∠3=240°,则∠4等于( )
A. 80° B. 70°
C. 60° D. 50°
B
3. (2021·岳阳)将一副直角三角板按如图D5-1-21所示的方式摆放,若直线a∥b,则∠1的大小为( )
A. 45°
B. 60°
C. 75°
D. 105°
C
4. (2021·达州)如图D5-1-22,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=40°时,∠DCN的度数为( )
A. 40° B. 50°
C. 60° D. 80°
B
5. (2021·贵港)如图D5-1-23,AB∥CD,CB平分∠ECD,若∠B=26°,则∠1的度数是____________.
52°
6. (2021·恩施州)如图D5-1-24,已知AE∥BC,若∠BAC=100°,∠DAE=50°,则∠C=____________.
30°
7. (2021·张家界)如图D5-1-25,已知AB∥CD,BC是∠ABD的平分线,若∠2=64°,则∠3=__________.
58°
8. (2019·武汉)如图D5-1-26,点A,B,C,D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF,求证:∠E=∠F.
证明:∵∠A=∠1,
∴AE∥BF. ∴∠2=∠E.
∵CE∥DF,∴∠2=∠F.
∴∠E=∠F.
谢 谢
