人教版数学七年级下册 第七章 平面直角坐标系 过关训练 课件(共29张PPT)
文档属性
| 名称 | 人教版数学七年级下册 第七章 平面直角坐标系 过关训练 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 505.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 19:51:21 | ||
图片预览








文档简介
(共29张PPT)
第七章过关训练
一、选择题(本大题12小题,每小题3分,共36分)
1. 在平面直角坐标系中,点(-4,4)所在的象限是( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
2.在平面内,根据下列表述,能确定位置的是( )
A. 华创电影院2排 B. 北偏东50°
C. 东经118°,北纬30° D. 保定市普育路
B
C
3.若点P(m,1)在第二象限内,则点Q(-m,0)在( )
A. x轴正半轴上 B. x轴负半轴上
C. y轴正半轴上 D. y轴负半轴上
4.点A(m,n)满足m=0,则点A在( )
A. 原点 B. 坐标轴上
C. x轴上 D. y轴上
A
D
5.点M在x轴的上方、y轴的左侧,且点M到x轴、y轴的距离分别为3和5,则点M的坐标为( )
A. (-5,3) B. (5,-3)
C. (-3,5) D. (3,-5)
6.在平面直角坐标系中,点P(a,a-3)的位置一定不在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
A
B
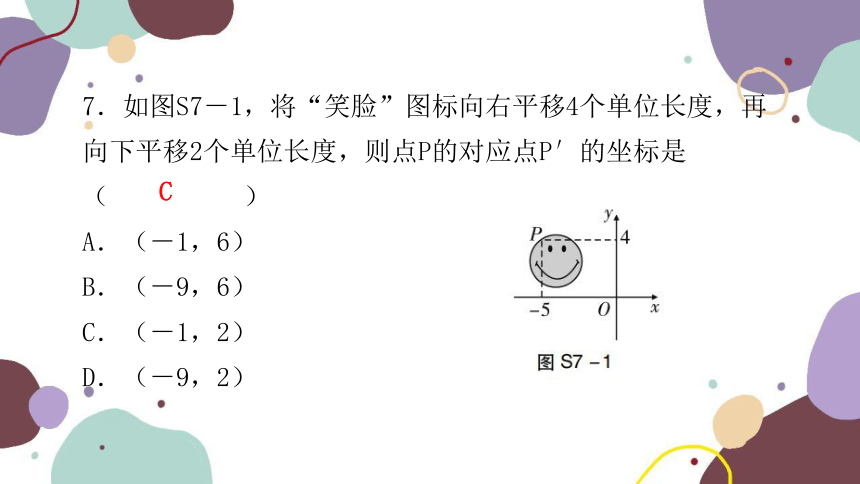
7.如图S7-1,将“笑脸”图标向右平移4个单位长度,再向下平移2个单位长度,则点P的对应点P′的坐标是( )
A.(-1,6)
B.(-9,6)
C.(-1,2)
D.(-9,2)
C
8. 下列说法错误的是( )
A. 原点的坐标是(0,0)
B. x轴上的所有点的纵坐标都相等
C. y轴上的所有点的横坐标都相等
D. 点(0,-1)在第四象限
D
9. 将三角形ABC的三个顶点的横坐标都减1,纵坐标不变,则所得图形与原图形的位置关系是( )
A. 将原图形向x轴的正方向平移了1个单位长度
B. 将原图形向x轴的负方向平移了1个单位长度
C. 将原图形向y轴的正方向平移了1个单位长度
D. 将原图形向y轴的负方向平移了1个单位长度
B
10.在平面直角坐标系中,已知线段AB的两个端点分别是A(-4,-1),B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(-2,2),则点B′的坐标为( )
A. (4,3) B. (3,4)
C. (-1,-2) D. (-2,-1)
B
11.若点P(x,y)在第二象限,且|x|=2,|y|=3,则x+y=( )
A. -1 B. 1 C. 5 D. -5
12. 下列说法正确的是( )
A. 若ab=0,则点P(a,b)表示原点
B. 点(-1,-a)在第三象限
C. 已知点A(3,-3)与点B(3,3),则直线AB∥x轴
D. 若ab>0,则点P(a,b)在第一、三象限
B
D
二、填空题(本大题6小题,每小题4分,共24分)
13.点(-3,5)到x轴的距离是________________,到y轴的距离是________________.
14.在平面直角坐标系中,已知点A(3,2),AC⊥x轴,垂足为点C,则点C的坐标为________________.
15.在平面直角坐标系中,将点(3,-2)先向右平移2个单位长度,再向上平移3个单位长度,则所得点的坐标是________________.
5
3
(3,0)
(5,1)
16.已知点P位于x轴上方距离x轴5个单位长度,距离y轴7个单位长度,则点P的坐标为_________________________.
17.若点A(3,x+1),B(2y-1,-1)分别在x轴、y轴上,
则x2+y2=________________.
(7,5)或(-7,5)
18.如图S7-2,在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,再选定一个单位长度和角度的正方向(通常取逆时针方向).对于平面内任何一点M,用ρ表示线段OM的长度,θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对(ρ,θ)就叫
点M的极坐标,若ON⊥Ox,且点N到极点O
的距离为4个单位长度,则点N的极坐标
可表示为______________________.
(4,90°)
三、解答题(一)(本大题2小题,每小题8分,共16分)
19.某市有A,B,C,D四个大型超市,分别位于一条东西走向的平安大路两侧,如图S7-3.若C(-2,8),D(0,0),请建立适当的直角坐标系,并写出A,B两个超市相应的坐标.
解:建立平面直角坐标系如答图S7-1.
点A的坐标为(10,9),点B的坐标为(6,-1).
20.已知点P(a,b)在第二象限,且|a|=3,|b|=8,求点P的坐标.
解:由第二象限内的点的横坐标小于零,得a=-3.
由第二象限内的点的纵坐标大于零,得b=8.
故点P的坐标是(-3,8).
四、解答题(二)(本大题2小题,每小题10分,共20分)
21. 已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点Q的坐标为(1,5),直线PQ∥y轴.
解:(1)∵点P(a-2,2a+8)在x轴上,
∴2a+8=0,解得a=-4.
∴a-2=-4-2=-6.
∴点P的坐标是(-6,0).
(2)∵点P(a-2,2a+8)在y轴上,
∴a-2=0,解得a=2.
∴2a+8=2×2+8=12.
∴点P的坐标是(0,12).
(3)∵点Q的坐标为(1,5),直线PQ∥y轴,
∴a-2=1,解得a=3.
∴2a+8=14.
∴点P的坐标是(1,14).
22.如图S7-4,雷达探测器测得六个目标A,B,C,D,E,F出现,按照规定的目标表示方法,目标C,F的位置表示为C(6,120°),F(5,210°).
(1)按照此方法表示目标A,B,D,E的位置.
A________________,
B________________,
D________________,
E_______________;
(5,30°)
(2,90°)
(4,240°)
(3,300°)
(2)若目标C的实际位置是北偏西30°距观测站1 800 m,目标F的实际位置是南偏西60°距观测站1 500 m,写出目标A,B,D,E的实际位置;
(3)若另有目标G在东南方向距观测站750 m处,目标H在南偏东20°距观测站900 m处,写出G,H的位置表示.
解:(2)根据上北下南左西右东确定角度,用横坐标乘300确定距离,
∴目标A的实际位置为北偏东60°距观测站1 500 m,目标B的实际位置为正北方向距观测站600 m,目标D的实际位置为南偏西30°距观测站1 200 m,目标E的实际位置为南偏东30°距观测站900 m.
(3)用(2)的反向方法计算可得G(2.5,315°),
H(3,290°).
五、解答题(三)(本大题2小题,每小题12分,共24分)
23.如图S7-5为某中学新校区分布图的一部分,方格纸中每个小方格都是边长为1个单位长度的正方形.若教学楼的坐标为A(1,2),图书馆的坐
标为B(-2,-1),解答以下
问题:
(1)在图中找到坐标系中的原点,并画出平面直角坐标系;
(2)若体育馆的坐标为C(0,-1),食堂坐标为D(3,2),请在图中标出体育馆和食堂的位置;
(3)顺次连接点A,B,C,D得到四边形ABCD,求四边形ABCD的面积.
解:(1)原点O和平面直角坐标系如答图S7-2.
(2)体育馆和食堂的位置如答图S7-2.
(3)四边形ABCD如答图S7-2.
∵四边形ABCD是平行四边形,
∴四边形ABCD的面积为2×3=6.
24.如图S7-6,在平面直角坐标系中,A(0,1),B(2,0),C(4,3).
(1)画出三角形ABC;
(2)求三角形ABC的面积;
(3)设点P在x轴上,且三角形ABP与
三角形ABC的面积相等,求点P的坐标.
解:(1)三角形ABC如答图S7-3.
谢 谢
第七章过关训练
一、选择题(本大题12小题,每小题3分,共36分)
1. 在平面直角坐标系中,点(-4,4)所在的象限是( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
2.在平面内,根据下列表述,能确定位置的是( )
A. 华创电影院2排 B. 北偏东50°
C. 东经118°,北纬30° D. 保定市普育路
B
C
3.若点P(m,1)在第二象限内,则点Q(-m,0)在( )
A. x轴正半轴上 B. x轴负半轴上
C. y轴正半轴上 D. y轴负半轴上
4.点A(m,n)满足m=0,则点A在( )
A. 原点 B. 坐标轴上
C. x轴上 D. y轴上
A
D
5.点M在x轴的上方、y轴的左侧,且点M到x轴、y轴的距离分别为3和5,则点M的坐标为( )
A. (-5,3) B. (5,-3)
C. (-3,5) D. (3,-5)
6.在平面直角坐标系中,点P(a,a-3)的位置一定不在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
A
B
7.如图S7-1,将“笑脸”图标向右平移4个单位长度,再向下平移2个单位长度,则点P的对应点P′的坐标是( )
A.(-1,6)
B.(-9,6)
C.(-1,2)
D.(-9,2)
C
8. 下列说法错误的是( )
A. 原点的坐标是(0,0)
B. x轴上的所有点的纵坐标都相等
C. y轴上的所有点的横坐标都相等
D. 点(0,-1)在第四象限
D
9. 将三角形ABC的三个顶点的横坐标都减1,纵坐标不变,则所得图形与原图形的位置关系是( )
A. 将原图形向x轴的正方向平移了1个单位长度
B. 将原图形向x轴的负方向平移了1个单位长度
C. 将原图形向y轴的正方向平移了1个单位长度
D. 将原图形向y轴的负方向平移了1个单位长度
B
10.在平面直角坐标系中,已知线段AB的两个端点分别是A(-4,-1),B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(-2,2),则点B′的坐标为( )
A. (4,3) B. (3,4)
C. (-1,-2) D. (-2,-1)
B
11.若点P(x,y)在第二象限,且|x|=2,|y|=3,则x+y=( )
A. -1 B. 1 C. 5 D. -5
12. 下列说法正确的是( )
A. 若ab=0,则点P(a,b)表示原点
B. 点(-1,-a)在第三象限
C. 已知点A(3,-3)与点B(3,3),则直线AB∥x轴
D. 若ab>0,则点P(a,b)在第一、三象限
B
D
二、填空题(本大题6小题,每小题4分,共24分)
13.点(-3,5)到x轴的距离是________________,到y轴的距离是________________.
14.在平面直角坐标系中,已知点A(3,2),AC⊥x轴,垂足为点C,则点C的坐标为________________.
15.在平面直角坐标系中,将点(3,-2)先向右平移2个单位长度,再向上平移3个单位长度,则所得点的坐标是________________.
5
3
(3,0)
(5,1)
16.已知点P位于x轴上方距离x轴5个单位长度,距离y轴7个单位长度,则点P的坐标为_________________________.
17.若点A(3,x+1),B(2y-1,-1)分别在x轴、y轴上,
则x2+y2=________________.
(7,5)或(-7,5)
18.如图S7-2,在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,再选定一个单位长度和角度的正方向(通常取逆时针方向).对于平面内任何一点M,用ρ表示线段OM的长度,θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对(ρ,θ)就叫
点M的极坐标,若ON⊥Ox,且点N到极点O
的距离为4个单位长度,则点N的极坐标
可表示为______________________.
(4,90°)
三、解答题(一)(本大题2小题,每小题8分,共16分)
19.某市有A,B,C,D四个大型超市,分别位于一条东西走向的平安大路两侧,如图S7-3.若C(-2,8),D(0,0),请建立适当的直角坐标系,并写出A,B两个超市相应的坐标.
解:建立平面直角坐标系如答图S7-1.
点A的坐标为(10,9),点B的坐标为(6,-1).
20.已知点P(a,b)在第二象限,且|a|=3,|b|=8,求点P的坐标.
解:由第二象限内的点的横坐标小于零,得a=-3.
由第二象限内的点的纵坐标大于零,得b=8.
故点P的坐标是(-3,8).
四、解答题(二)(本大题2小题,每小题10分,共20分)
21. 已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点Q的坐标为(1,5),直线PQ∥y轴.
解:(1)∵点P(a-2,2a+8)在x轴上,
∴2a+8=0,解得a=-4.
∴a-2=-4-2=-6.
∴点P的坐标是(-6,0).
(2)∵点P(a-2,2a+8)在y轴上,
∴a-2=0,解得a=2.
∴2a+8=2×2+8=12.
∴点P的坐标是(0,12).
(3)∵点Q的坐标为(1,5),直线PQ∥y轴,
∴a-2=1,解得a=3.
∴2a+8=14.
∴点P的坐标是(1,14).
22.如图S7-4,雷达探测器测得六个目标A,B,C,D,E,F出现,按照规定的目标表示方法,目标C,F的位置表示为C(6,120°),F(5,210°).
(1)按照此方法表示目标A,B,D,E的位置.
A________________,
B________________,
D________________,
E_______________;
(5,30°)
(2,90°)
(4,240°)
(3,300°)
(2)若目标C的实际位置是北偏西30°距观测站1 800 m,目标F的实际位置是南偏西60°距观测站1 500 m,写出目标A,B,D,E的实际位置;
(3)若另有目标G在东南方向距观测站750 m处,目标H在南偏东20°距观测站900 m处,写出G,H的位置表示.
解:(2)根据上北下南左西右东确定角度,用横坐标乘300确定距离,
∴目标A的实际位置为北偏东60°距观测站1 500 m,目标B的实际位置为正北方向距观测站600 m,目标D的实际位置为南偏西30°距观测站1 200 m,目标E的实际位置为南偏东30°距观测站900 m.
(3)用(2)的反向方法计算可得G(2.5,315°),
H(3,290°).
五、解答题(三)(本大题2小题,每小题12分,共24分)
23.如图S7-5为某中学新校区分布图的一部分,方格纸中每个小方格都是边长为1个单位长度的正方形.若教学楼的坐标为A(1,2),图书馆的坐
标为B(-2,-1),解答以下
问题:
(1)在图中找到坐标系中的原点,并画出平面直角坐标系;
(2)若体育馆的坐标为C(0,-1),食堂坐标为D(3,2),请在图中标出体育馆和食堂的位置;
(3)顺次连接点A,B,C,D得到四边形ABCD,求四边形ABCD的面积.
解:(1)原点O和平面直角坐标系如答图S7-2.
(2)体育馆和食堂的位置如答图S7-2.
(3)四边形ABCD如答图S7-2.
∵四边形ABCD是平行四边形,
∴四边形ABCD的面积为2×3=6.
24.如图S7-6,在平面直角坐标系中,A(0,1),B(2,0),C(4,3).
(1)画出三角形ABC;
(2)求三角形ABC的面积;
(3)设点P在x轴上,且三角形ABP与
三角形ABC的面积相等,求点P的坐标.
解:(1)三角形ABC如答图S7-3.
谢 谢
