2021-2022学年高二上学期数学人教A版(2019)选择性必修第三册7.2.1离散型随机变量课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第三册7.2.1离散型随机变量课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 360.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
7.2.1离散型随机变量
学习目标:
1、理解随机变量的意义;
2、学会区分离散型与连续型随机 变量,并能举出离散性随机变量
的例子;
3、理解随机变量所表示试验结果的含义,并恰当地定义随机变量。
问题1:某人在射击训练中,射击一次,命中的环数。
问题2:某纺织公司的某次产品检验,在可能含有
次品的100件产品中任意抽取4件,其中含有的次品
件数。
试验的结果 …
用数字表示试验结果 …
试验的结果
用数字表示试验结果
命中0环
命中1环
命中2环
命中10环
0
1
2
10
抽到0件次品
抽到1件次品
抽到2件次品
抽到3件次品
抽到4件次品
0
1
2
3
4
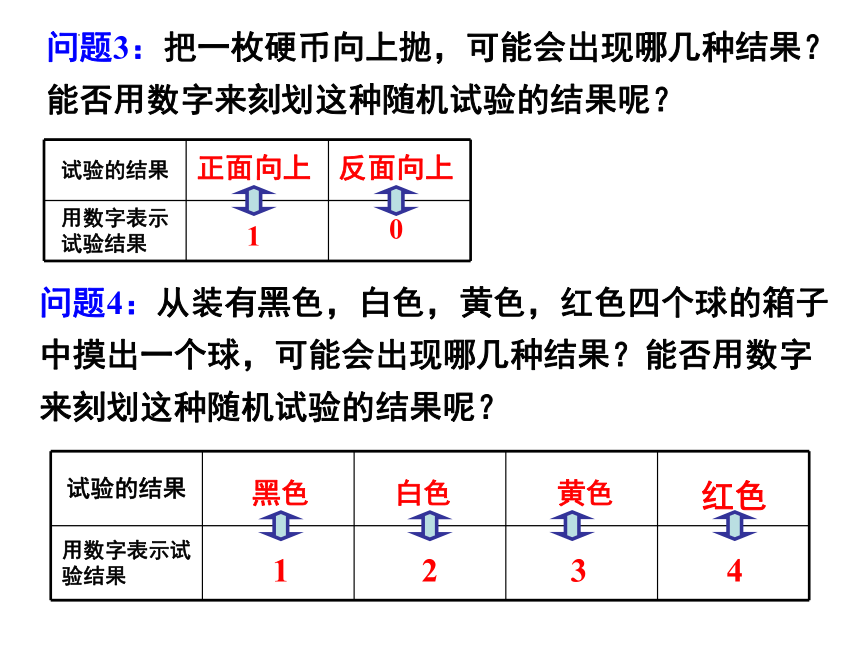
问题3:把一枚硬币向上抛,可能会出现哪几种结果?能否用数字来刻划这种随机试验的结果呢?
问题4:从装有黑色,白色,黄色,红色四个球的箱子中摸出一个球,可能会出现哪几种结果?能否用数字来刻划这种随机试验的结果呢?
试验的结果
用数字表示试验结果
正面向上
反面向上
1
0
试验的结果
用数字表示试验结果
黑色
白色
黄色
红色
1
2
3
4
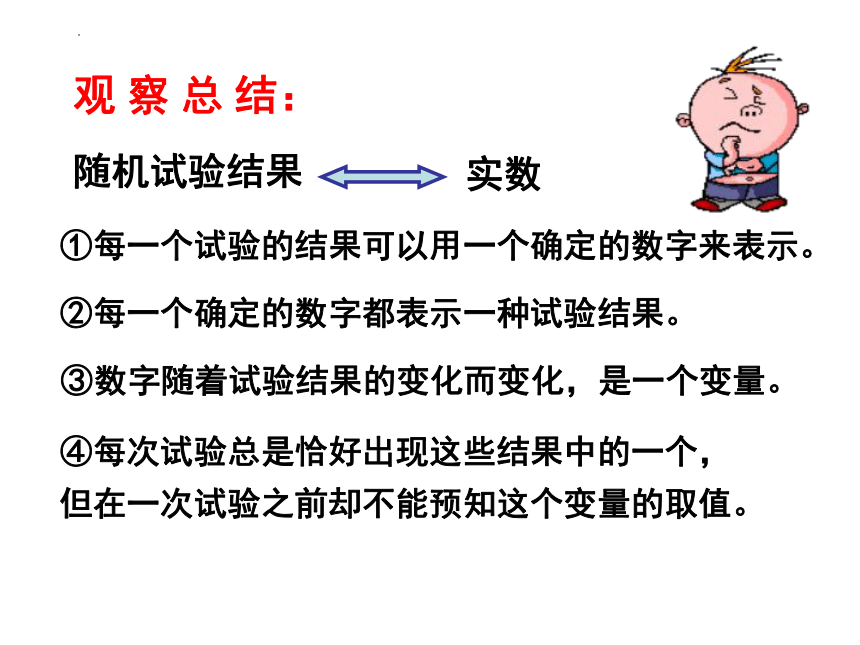
①每一个试验的结果可以用一个确定的数字来表示。
②每一个确定的数字都表示一种试验结果。
③数字随着试验结果的变化而变化,是一个变量。
④每次试验总是恰好出现这些结果中的一个,
但在一次试验之前却不能预知这个变量的取值。
观 察 总 结:
实数
随机试验结果
随机变量常用希腊字母X、Y、ξ、η等表示。
一、随机变量:
在随机试验中,确定了一个对应关系,使得每一个试验结果都用一个确定的数字表示。在这个对应关系下,数字随着试验结果变化而变化,像这样随着试验结果变化而变化的变量称做随机变量。
随机变量X或ξ或η的特点:
(1)可以用数表示;
(2)试验之前可以判断其可能出现的所有值;
(3)在试验之前不可能确定取何值。
例如:
在问题1中:某人射击一次,命中的环数为ξ。
ξ=0,表示命中 0 环;
ξ=1,表示命中 1 环;
ξ=10,表示命中 10 环;
在问题2中:产品检查任意抽取 4件, 含有的次品数为η。
η=0,表示含有 0 个次品;
η=1,表示含有 1 个次品;
η=2,表示含有 2 个次品;
η=4,表示含有 4 个次品;
练习:判断下列各个量,哪些是随机变量,哪些不是随机变量,并说明理由。
(1)袋中装有6个红球,4个白球,取3个球其中
白球的个数;
(2)标准大气压下,水沸腾的温度;
(3)在一次比赛中,设一二三等奖,你的作品获得的奖次;
(4)体积64立方米的正方体的棱长;
(5)抛掷两次骰子,两次结果的和;
(6)某天博文学校校办接到的电话的个数。
解:(1)(3)(5)(6)
随机变量和函数都一种映射。
随机变量把随机试验的结果映射为实数,
函数把实数映射为实数。
试验结果的范围相当于函数的定义域,
随机变量的取值范围相当于函数的值域。
随机变量的取值范围叫做随机变量的值域。
思考:随机变量和函数的联系和区别:
在上面的射击、产品检验等例子中,对于随机变量可能取的值,我们都可以按一定次序一一列出,这样的随机变量叫做离散型随机变量。
二、离散型随机变量:
在上面的无故障运转时间、树木高度等例子中,
随机变量可以取某一区间内的一切值,这样的
随机变量叫做连续型随机变量。
例1:某林场树木最高达30m,则此林场树木的
高度η是一个随机变量,它可以取(0,30]。
例2:某一自动装置无故障运转的时间ξ是一个
随机变量,它可以取区间(0,+∞)内的一切值。
三、连续型随机变量:
有的随机变量,它可以取某一区间内的一切值,看下面的例子。
例3:写出下列随机变量可能取的值,并说明
随机变量所取的值表示的随机试验的结果。
一袋中装有5只同样大小的白球,编号为1,2,3,4,5。现从该袋内随机取出3只球,被取出的球的最大号码数 。
解:
=3,4,5
表示取出的3个球的编号为1,2,3。
表示取出的3个球的编号为1,2,4或1,3,4或2,3,4 。
表示取出的3个球的编号为1,2,5或1,3,5或1,4,5
或2,3,5或2,4,5或3,4,5。
(1)从10张已编号的卡片(从1号到10号)中任取 1张,被取出的卡片的号数ξ。
练习:写出下列各随机变量可能取的值,并说明随机变量所取的值所表示的随机试验的结果。
(2)一个袋中装有5个白球和5个黑球,从中任取3个,其中所含白球的个数ξ。
(3)抛掷两个骰子,所得点数之和是ξ。
ξ=1,2,…,10
ξ=0,1,2, 3
ξ=2,3,… ,12
(4)连续不断地射击,首次命中目标需要的射击次数η。
=1,2,…,n,….
注:随机变量的取值可以是有限个,也可是无限个。
例4:某人去商厦为所在公司购买玻璃水杯若干只,单价6元。公司要求至少要买50只,但不得超过80只。商厦有优惠规定:一次购买这种水杯小于或等于50只的不优惠,大于50只的,超出的部分按原价格的7折优惠。 这个人一次购买水杯的只数ξ是否为一个随机变量,他所付款是否也为一个随机变量呢?这两个随机变量有什么关系呢?
显然,η也是随机变量。
【总一总★成竹在胸】
4、若ξ是随机变量,则η=aξ+b
(其中a、b 是常数)也是随机变量。
2、随机变量分为离散型随机变量和连续型随机变量。
3、某些随机试验的结果不具备数量性质,但仍可以用数量来表示它。
1、随机变量将随机事件的结果数量化。
随机变量ξ的取值对应于随机试验的某一随机事件。
再见
7.2.1离散型随机变量
学习目标:
1、理解随机变量的意义;
2、学会区分离散型与连续型随机 变量,并能举出离散性随机变量
的例子;
3、理解随机变量所表示试验结果的含义,并恰当地定义随机变量。
问题1:某人在射击训练中,射击一次,命中的环数。
问题2:某纺织公司的某次产品检验,在可能含有
次品的100件产品中任意抽取4件,其中含有的次品
件数。
试验的结果 …
用数字表示试验结果 …
试验的结果
用数字表示试验结果
命中0环
命中1环
命中2环
命中10环
0
1
2
10
抽到0件次品
抽到1件次品
抽到2件次品
抽到3件次品
抽到4件次品
0
1
2
3
4
问题3:把一枚硬币向上抛,可能会出现哪几种结果?能否用数字来刻划这种随机试验的结果呢?
问题4:从装有黑色,白色,黄色,红色四个球的箱子中摸出一个球,可能会出现哪几种结果?能否用数字来刻划这种随机试验的结果呢?
试验的结果
用数字表示试验结果
正面向上
反面向上
1
0
试验的结果
用数字表示试验结果
黑色
白色
黄色
红色
1
2
3
4
①每一个试验的结果可以用一个确定的数字来表示。
②每一个确定的数字都表示一种试验结果。
③数字随着试验结果的变化而变化,是一个变量。
④每次试验总是恰好出现这些结果中的一个,
但在一次试验之前却不能预知这个变量的取值。
观 察 总 结:
实数
随机试验结果
随机变量常用希腊字母X、Y、ξ、η等表示。
一、随机变量:
在随机试验中,确定了一个对应关系,使得每一个试验结果都用一个确定的数字表示。在这个对应关系下,数字随着试验结果变化而变化,像这样随着试验结果变化而变化的变量称做随机变量。
随机变量X或ξ或η的特点:
(1)可以用数表示;
(2)试验之前可以判断其可能出现的所有值;
(3)在试验之前不可能确定取何值。
例如:
在问题1中:某人射击一次,命中的环数为ξ。
ξ=0,表示命中 0 环;
ξ=1,表示命中 1 环;
ξ=10,表示命中 10 环;
在问题2中:产品检查任意抽取 4件, 含有的次品数为η。
η=0,表示含有 0 个次品;
η=1,表示含有 1 个次品;
η=2,表示含有 2 个次品;
η=4,表示含有 4 个次品;
练习:判断下列各个量,哪些是随机变量,哪些不是随机变量,并说明理由。
(1)袋中装有6个红球,4个白球,取3个球其中
白球的个数;
(2)标准大气压下,水沸腾的温度;
(3)在一次比赛中,设一二三等奖,你的作品获得的奖次;
(4)体积64立方米的正方体的棱长;
(5)抛掷两次骰子,两次结果的和;
(6)某天博文学校校办接到的电话的个数。
解:(1)(3)(5)(6)
随机变量和函数都一种映射。
随机变量把随机试验的结果映射为实数,
函数把实数映射为实数。
试验结果的范围相当于函数的定义域,
随机变量的取值范围相当于函数的值域。
随机变量的取值范围叫做随机变量的值域。
思考:随机变量和函数的联系和区别:
在上面的射击、产品检验等例子中,对于随机变量可能取的值,我们都可以按一定次序一一列出,这样的随机变量叫做离散型随机变量。
二、离散型随机变量:
在上面的无故障运转时间、树木高度等例子中,
随机变量可以取某一区间内的一切值,这样的
随机变量叫做连续型随机变量。
例1:某林场树木最高达30m,则此林场树木的
高度η是一个随机变量,它可以取(0,30]。
例2:某一自动装置无故障运转的时间ξ是一个
随机变量,它可以取区间(0,+∞)内的一切值。
三、连续型随机变量:
有的随机变量,它可以取某一区间内的一切值,看下面的例子。
例3:写出下列随机变量可能取的值,并说明
随机变量所取的值表示的随机试验的结果。
一袋中装有5只同样大小的白球,编号为1,2,3,4,5。现从该袋内随机取出3只球,被取出的球的最大号码数 。
解:
=3,4,5
表示取出的3个球的编号为1,2,3。
表示取出的3个球的编号为1,2,4或1,3,4或2,3,4 。
表示取出的3个球的编号为1,2,5或1,3,5或1,4,5
或2,3,5或2,4,5或3,4,5。
(1)从10张已编号的卡片(从1号到10号)中任取 1张,被取出的卡片的号数ξ。
练习:写出下列各随机变量可能取的值,并说明随机变量所取的值所表示的随机试验的结果。
(2)一个袋中装有5个白球和5个黑球,从中任取3个,其中所含白球的个数ξ。
(3)抛掷两个骰子,所得点数之和是ξ。
ξ=1,2,…,10
ξ=0,1,2, 3
ξ=2,3,… ,12
(4)连续不断地射击,首次命中目标需要的射击次数η。
=1,2,…,n,….
注:随机变量的取值可以是有限个,也可是无限个。
例4:某人去商厦为所在公司购买玻璃水杯若干只,单价6元。公司要求至少要买50只,但不得超过80只。商厦有优惠规定:一次购买这种水杯小于或等于50只的不优惠,大于50只的,超出的部分按原价格的7折优惠。 这个人一次购买水杯的只数ξ是否为一个随机变量,他所付款是否也为一个随机变量呢?这两个随机变量有什么关系呢?
显然,η也是随机变量。
【总一总★成竹在胸】
4、若ξ是随机变量,则η=aξ+b
(其中a、b 是常数)也是随机变量。
2、随机变量分为离散型随机变量和连续型随机变量。
3、某些随机试验的结果不具备数量性质,但仍可以用数量来表示它。
1、随机变量将随机事件的结果数量化。
随机变量ξ的取值对应于随机试验的某一随机事件。
再见
