【课件】4.4 数学探究活动:了解高考选考科目的确定是否与性别有关 数学-RJB-选择性必修第二册-第四章-概率与统计(共31张PPT)
文档属性
| 名称 | 【课件】4.4 数学探究活动:了解高考选考科目的确定是否与性别有关 数学-RJB-选择性必修第二册-第四章-概率与统计(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
数学-RJ·B-选择性必修第二册
4.4 数学探究活动:了解高考选考科目的确定是否与性别有关
第四章 概率与统计
学习目标
1.了解独立性检验的基本思想.
2.理解判断两个分类变量是否有关系的常用方法.
3.理解独立性检验中的含义及其实施步骤.
重点:理解独立性检验的基本思想及实施步骤.
难点:了解独立性检验的基本思想;了解随机变量的含义, 的观测值很大,就认为两个分类变量是有关系的.
知识梳理
一 列联表
1.2×2列联表的定义
A 总计
B a b a+b
c d c+d
总计 a+c b+d a+b+c+d
因为这个表格中,核心的数据是中间的4个格子,所以这样的表格通常称为2×2列联表.
二 独立性检验
例1
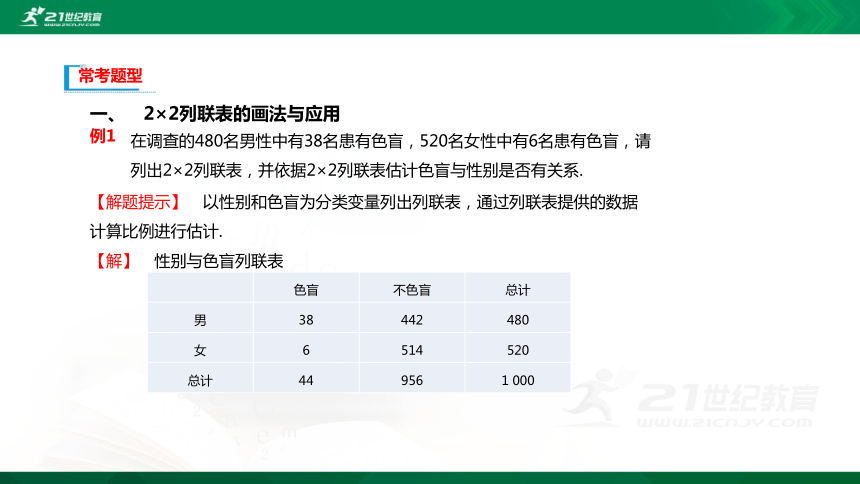
一、 2×2列联表的画法与应用
在调查的480名男性中有38名患有色盲,520名女性中有6名患有色盲,请列出2×2列联表,并依据2×2列联表估计色盲与性别是否有关系.
【解题提示】 以性别和色盲为分类变量列出列联表,通过列联表提供的数据计算比例进行估计.
【解】 性别与色盲列联表
色盲 不色盲 总计
男 38 442 480
女 6 514 520
总计 44 956 1 000
常考题型
2×2列联表的画法及应用
1.列出的两个分类变量的频数表,称为列联表.
2.假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为
解题归纳
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
3.在实际应用中,通常要求a,b,c,d都不小于5.
训练题
[2020·河北张家口高三检测]某学生对其亲属30人的饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:饮食指数低于70的人,饮食以蔬菜为主,饮食指数高于70的人,饮食以肉类为主)
根据以上数据完成下面2×2列联表:
主食蔬菜 主食肉类 总计
50岁以下 4 8 12
50岁以上 16 2 18
总计 20 10 30
解题归纳
例2
二 独立性检验
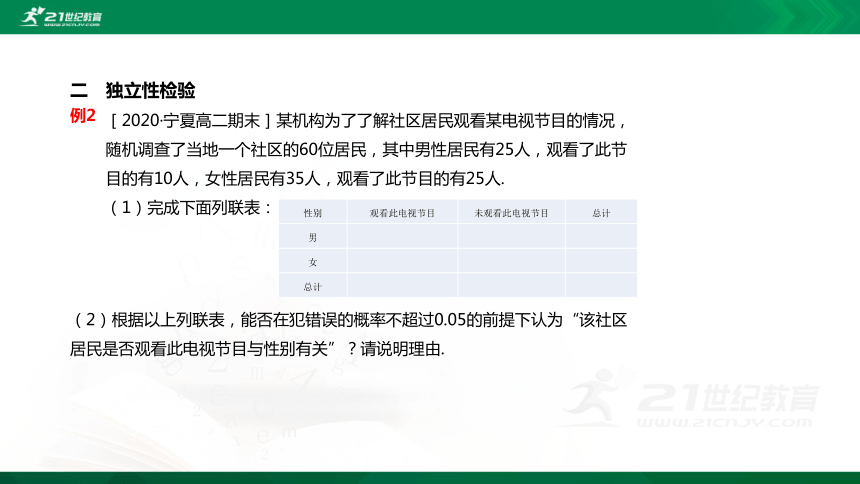
[2020·宁夏高二期末]某机构为了了解社区居民观看某电视节目的情况,随机调查了当地一个社区的60位居民,其中男性居民有25人,观看了此节目的有10人,女性居民有35人,观看了此节目的有25人.
(1)完成下面列联表:
性别 观看此电视节目 未观看此电视节目 总计
男
女
总计
(2)根据以上列联表,能否在犯错误的概率不超过0.05的前提下认为“该社区居民是否观看此电视节目与性别有关”?请说明理由.
【解】 (1)
性别 观看此电视节目 未观看此电视节目 总计
男 10 15 25
女 25 10 35
总计 35 25 60
解题归纳
独立性检验的方法
利用K2的观测值k较精确地给出判断.具体的做法是:
(1)抽取样本;(2)列出2×2列联表;
(3)提出假设H0:两分类变量没有关系;(4)进行独立性检验.
①根据实际问题的需要确定容许推断“两个分类变量有关系”犯错误概率的上
界,确定临界值k0;
②根据观测数据计算得到随机变量K2的观测值k;
解题归纳
③如果k≥k0,就推断“X与Y有关系”,这种推断犯错误的概率不超过P(K2≥ k0),否则,就认为在犯错误的概率不超过P(K2≥k0)的前提下不能推断“X与Y有关系”,或者在样本数据中没有发现足够证据支持结论“X与Y有关系”.当得到的观测数据a,b,c,d都不小于5时,可以通过查阅下表来确定结论“X与Y有关系”的可信程度.
P(K2≥k0) 0.50 0.40 0.25 0.15 0.10
k0 0.455 0.708 1.323 2.072 2.706
P(K2≥k0) 0.05 0.025 0.010 0.005 0.001
k0 3.841 5.024 6.635 7.879 10.828
训练题
C
1. [2020·广东揭阳高二期末]为了判定两个分类变量X和Y是否有关系,应用K2独立性检验法算得K2的观测值为5,又已知P (K2≥3.841)=0.05,P(K2≥6.635)=0.01,则下列说法正确的是 ( )
A.有99%以上的把握认为“X和Y有关系”
B.有99%以上的把握认为“X和Y没有关系”
C.有95%以上的把握认为“X和Y有关系”
D.有95%以上的把握认为“X和Y没有关系”
训练题
2. [2020·湖南宁乡一中高三月考]某媒体对“男女延迟退休”这一公众关注的问题进行民意调查,下表是在某单位得到的数据:
赞同 反对 总计
男 50 150 200
女 30 170 200
总计 80 320 400
(1)能否有97.5%的把握认为对这一问题的看法与性别有关?
(2)从赞同“男女延迟退休”的80人中,利用分层抽样的方法抽出8人,然后从中选出3人进行陈述发言,设发言的女士人数为X,求X的分布列和数学期望.
3.[2020·山西永济中学高二期末]为了解共享单车在A市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行分析,得到如下列联表: 单位:人
经常使用 偶尔使用或不使用 合计
30岁以下 70 30 100
30岁以上 60 40 100
合计 130 70 200
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为A市使用共享单车的情况与年龄有关?
(2) ①现从选取的30岁以上的网友中,采用分层抽样的方法选取10人,再从这10人中随机选出3人赠送优惠券,求选出的3人中至少有2人经常使用共享单车的概率.
②将频率视为概率,从A市所有参与调查的网友中随机选取10人赠送礼品,记其中经常使用共享单车的人数为X,求X的数学期望和方差.
解题归纳
独立性检验常与概率中的古典概型,统计中的离散型随机变量的分布列及数学期望和方差综合在一起.如本题在考查独立性检验思想的应用的同时,还考查了古典概型概率公式的应用,以及二项分布的数学期望和方差公式的应用,解题时要弄清随机变量所服从的分布列.
小结
A 总计
B a b a+b
c d c+d
总计 a+c b+d a+b+c+d
一 列联表
二 独立性检验
①根据实际问题的需要确定允许推断“两个分类变量有关”犯错误概率的上界,确定k的值;
②根据观测数据计算得到随机变量K2的值;
③如果K2≥k,就推断“两个分类变量有
关”,这种推断犯错误的概率不超过P(K2≥k),否则,就认为在犯错误的概率不超过P(K2≥k)的前提下不能推断“两个分类变量有关”或者在样本数据中没有发现足够的证据支持结论“两个分类变量有关”.当得到的观测数据a,b,c,d都不小于5时,可以通过查阅下表来确定结论“两个分类变量有关”的可信程度.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·B-选择性必修第二册
4.4 数学探究活动:了解高考选考科目的确定是否与性别有关
第四章 概率与统计
学习目标
1.了解独立性检验的基本思想.
2.理解判断两个分类变量是否有关系的常用方法.
3.理解独立性检验中的含义及其实施步骤.
重点:理解独立性检验的基本思想及实施步骤.
难点:了解独立性检验的基本思想;了解随机变量的含义, 的观测值很大,就认为两个分类变量是有关系的.
知识梳理
一 列联表
1.2×2列联表的定义
A 总计
B a b a+b
c d c+d
总计 a+c b+d a+b+c+d
因为这个表格中,核心的数据是中间的4个格子,所以这样的表格通常称为2×2列联表.
二 独立性检验
例1
一、 2×2列联表的画法与应用
在调查的480名男性中有38名患有色盲,520名女性中有6名患有色盲,请列出2×2列联表,并依据2×2列联表估计色盲与性别是否有关系.
【解题提示】 以性别和色盲为分类变量列出列联表,通过列联表提供的数据计算比例进行估计.
【解】 性别与色盲列联表
色盲 不色盲 总计
男 38 442 480
女 6 514 520
总计 44 956 1 000
常考题型
2×2列联表的画法及应用
1.列出的两个分类变量的频数表,称为列联表.
2.假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为
解题归纳
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
3.在实际应用中,通常要求a,b,c,d都不小于5.
训练题
[2020·河北张家口高三检测]某学生对其亲属30人的饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:饮食指数低于70的人,饮食以蔬菜为主,饮食指数高于70的人,饮食以肉类为主)
根据以上数据完成下面2×2列联表:
主食蔬菜 主食肉类 总计
50岁以下 4 8 12
50岁以上 16 2 18
总计 20 10 30
解题归纳
例2
二 独立性检验
[2020·宁夏高二期末]某机构为了了解社区居民观看某电视节目的情况,随机调查了当地一个社区的60位居民,其中男性居民有25人,观看了此节目的有10人,女性居民有35人,观看了此节目的有25人.
(1)完成下面列联表:
性别 观看此电视节目 未观看此电视节目 总计
男
女
总计
(2)根据以上列联表,能否在犯错误的概率不超过0.05的前提下认为“该社区居民是否观看此电视节目与性别有关”?请说明理由.
【解】 (1)
性别 观看此电视节目 未观看此电视节目 总计
男 10 15 25
女 25 10 35
总计 35 25 60
解题归纳
独立性检验的方法
利用K2的观测值k较精确地给出判断.具体的做法是:
(1)抽取样本;(2)列出2×2列联表;
(3)提出假设H0:两分类变量没有关系;(4)进行独立性检验.
①根据实际问题的需要确定容许推断“两个分类变量有关系”犯错误概率的上
界,确定临界值k0;
②根据观测数据计算得到随机变量K2的观测值k;
解题归纳
③如果k≥k0,就推断“X与Y有关系”,这种推断犯错误的概率不超过P(K2≥ k0),否则,就认为在犯错误的概率不超过P(K2≥k0)的前提下不能推断“X与Y有关系”,或者在样本数据中没有发现足够证据支持结论“X与Y有关系”.当得到的观测数据a,b,c,d都不小于5时,可以通过查阅下表来确定结论“X与Y有关系”的可信程度.
P(K2≥k0) 0.50 0.40 0.25 0.15 0.10
k0 0.455 0.708 1.323 2.072 2.706
P(K2≥k0) 0.05 0.025 0.010 0.005 0.001
k0 3.841 5.024 6.635 7.879 10.828
训练题
C
1. [2020·广东揭阳高二期末]为了判定两个分类变量X和Y是否有关系,应用K2独立性检验法算得K2的观测值为5,又已知P (K2≥3.841)=0.05,P(K2≥6.635)=0.01,则下列说法正确的是 ( )
A.有99%以上的把握认为“X和Y有关系”
B.有99%以上的把握认为“X和Y没有关系”
C.有95%以上的把握认为“X和Y有关系”
D.有95%以上的把握认为“X和Y没有关系”
训练题
2. [2020·湖南宁乡一中高三月考]某媒体对“男女延迟退休”这一公众关注的问题进行民意调查,下表是在某单位得到的数据:
赞同 反对 总计
男 50 150 200
女 30 170 200
总计 80 320 400
(1)能否有97.5%的把握认为对这一问题的看法与性别有关?
(2)从赞同“男女延迟退休”的80人中,利用分层抽样的方法抽出8人,然后从中选出3人进行陈述发言,设发言的女士人数为X,求X的分布列和数学期望.
3.[2020·山西永济中学高二期末]为了解共享单车在A市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行分析,得到如下列联表: 单位:人
经常使用 偶尔使用或不使用 合计
30岁以下 70 30 100
30岁以上 60 40 100
合计 130 70 200
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为A市使用共享单车的情况与年龄有关?
(2) ①现从选取的30岁以上的网友中,采用分层抽样的方法选取10人,再从这10人中随机选出3人赠送优惠券,求选出的3人中至少有2人经常使用共享单车的概率.
②将频率视为概率,从A市所有参与调查的网友中随机选取10人赠送礼品,记其中经常使用共享单车的人数为X,求X的数学期望和方差.
解题归纳
独立性检验常与概率中的古典概型,统计中的离散型随机变量的分布列及数学期望和方差综合在一起.如本题在考查独立性检验思想的应用的同时,还考查了古典概型概率公式的应用,以及二项分布的数学期望和方差公式的应用,解题时要弄清随机变量所服从的分布列.
小结
A 总计
B a b a+b
c d c+d
总计 a+c b+d a+b+c+d
一 列联表
二 独立性检验
①根据实际问题的需要确定允许推断“两个分类变量有关”犯错误概率的上界,确定k的值;
②根据观测数据计算得到随机变量K2的值;
③如果K2≥k,就推断“两个分类变量有
关”,这种推断犯错误的概率不超过P(K2≥k),否则,就认为在犯错误的概率不超过P(K2≥k)的前提下不能推断“两个分类变量有关”或者在样本数据中没有发现足够的证据支持结论“两个分类变量有关”.当得到的观测数据a,b,c,d都不小于5时,可以通过查阅下表来确定结论“两个分类变量有关”的可信程度.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
