人教版数学七年级下册 第五章过关训练 课件(共30张PPT)
文档属性
| 名称 | 人教版数学七年级下册 第五章过关训练 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 678.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-06 00:00:00 | ||
图片预览





文档简介
(共30张PPT)
第五章过关训练
一、选择题(本大题12小题,每小题3分,共36分)
1. 下列命题是真命题的( )
A. 两点之间直线最短
B. 如果ab>0,那么a>0,b>0
C. 内错角相等,两直线平行
D. 若|a|=1,则a=1
C
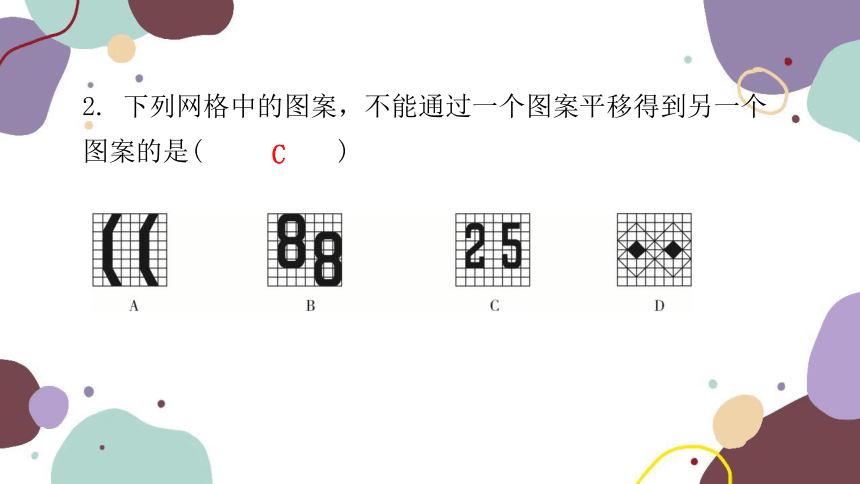
2. 下列网格中的图案,不能通过一个图案平移得到另一个图案的是( )
C
3. 下列说法正确的是( )
A. 图形的平移是指把图形沿水平方向移动
B. 平移前后图形的形状和大小都没有发生改变
C. “相等的角是对顶角”是一个真命题
D. “直角都相等”是一个假命题
B
4.如图S5-1,在平面内经过一点作已知直线m的平行线,可作平行线的条数有( )
A. 0条
B. 1条
C. 0条或1条
D. 无数条
C
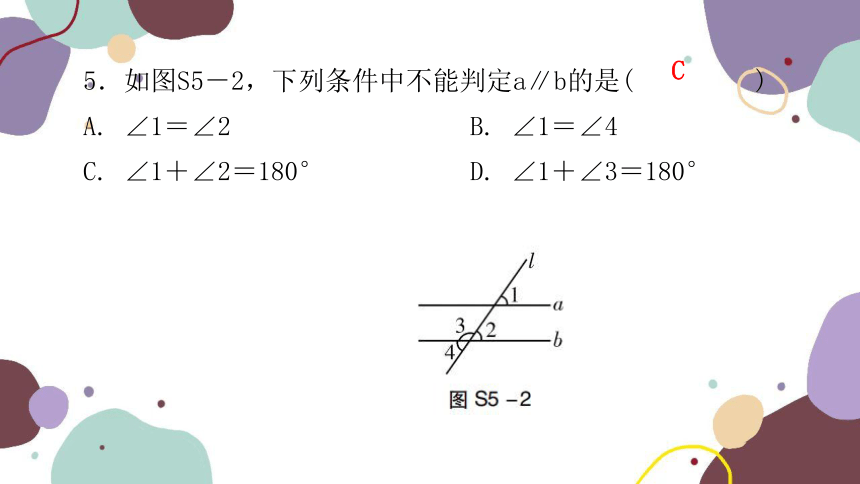
5.如图S5-2,下列条件中不能判定a∥b的是( )
A. ∠1=∠2 B. ∠1=∠4
C. ∠1+∠2=180° D. ∠1+∠3=180°
C
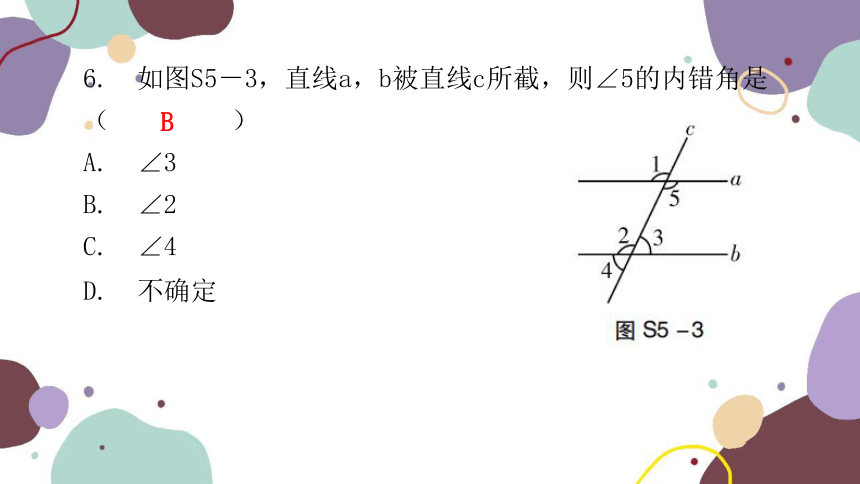
6. 如图S5-3,直线a,b被直线c所截,则∠5的内错角是( )
A. ∠3
B. ∠2
C. ∠4
D. 不确定
B
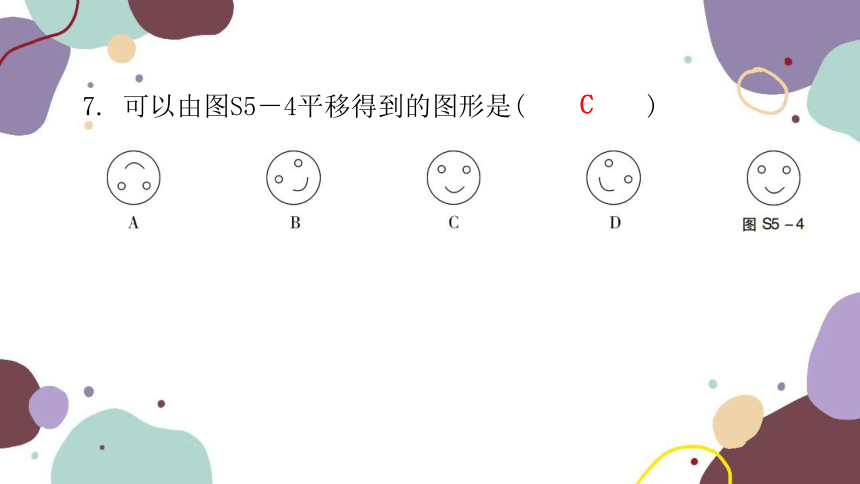
7. 可以由图S5-4平移得到的图形是( )
C
8.如图S5-5,下列条件:①∠2+∠4=180°;②∠4=∠5;③∠1=∠6;④∠1=∠3;⑤∠6=∠2.其中能判断直线l1∥l2的有( )
A. 2个
B. 3个
C. 4个
D. 5个
B
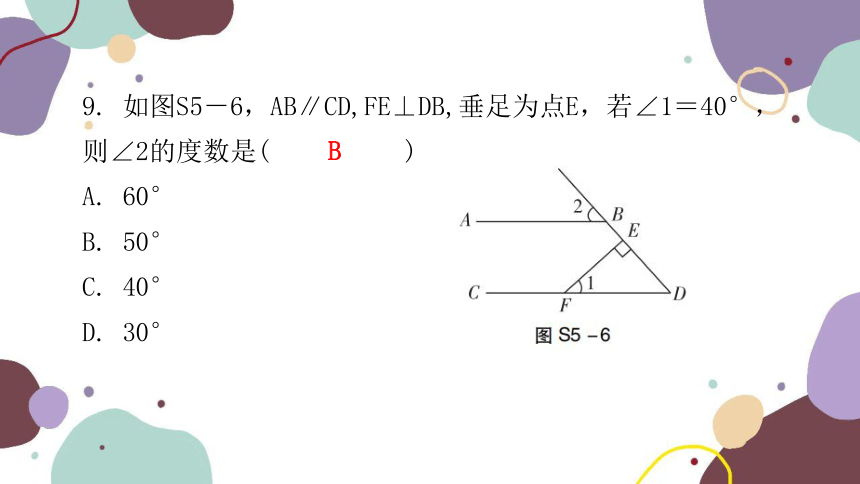
9. 如图S5-6,AB∥CD,FE⊥DB,垂足为点E,若∠1=40°,则∠2的度数是( )
A. 60°
B. 50°
C. 40°
D. 30°
B
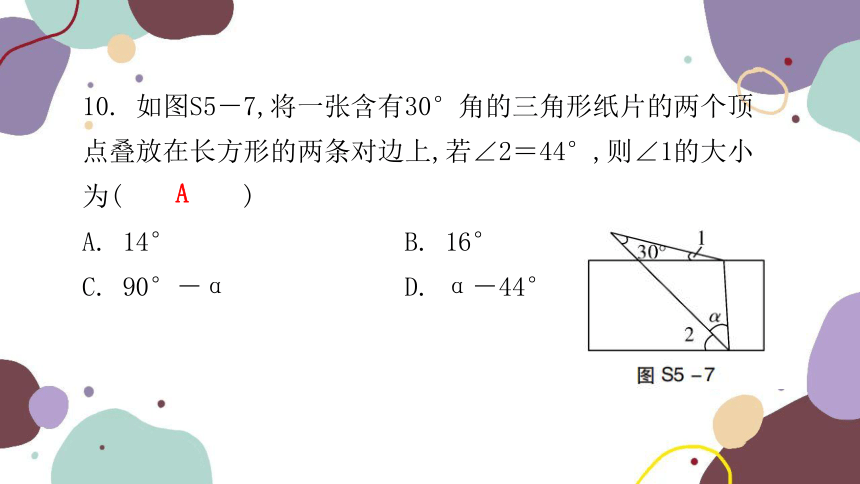
10. 如图S5-7,将一张含有30°角的三角形纸片的两个顶点叠放在长方形的两条对边上,若∠2=44°,则∠1的大小为( )
A. 14° B. 16°
C. 90°-α D. α-44°
A
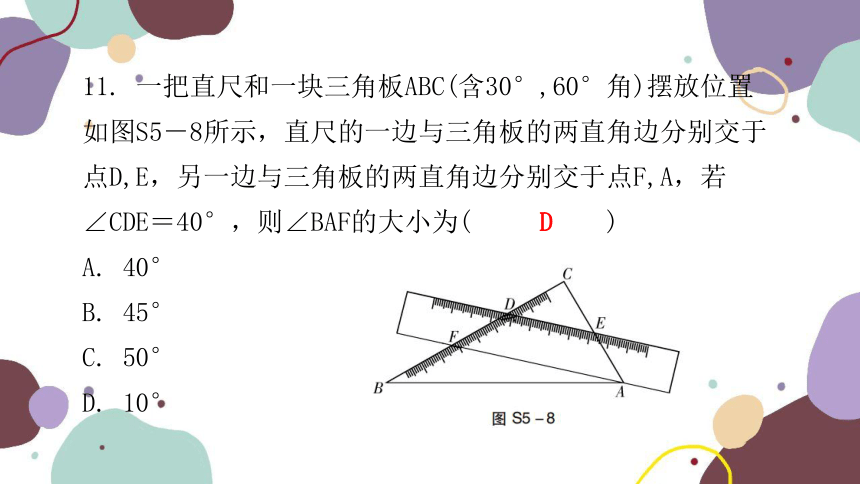
11. 一把直尺和一块三角板ABC(含30°,60°角)摆放位置如图S5-8所示,直尺的一边与三角板的两直角边分别交于点D,E,另一边与三角板的两直角边分别交于点F,A,若∠CDE=40°,则∠BAF的大小为( )
A. 40°
B. 45°
C. 50°
D. 10°
D
C
二、填空题(本大题6小题,每小题4分,共24分)
13.将命题“任意两个直角都相等”改写成“如果……那么……”的形式:___________________________________
___________________________________________________.
如果两个角都是直角,那么这两
个角相等
14.如图S5-10,∠ACB=90°,CD⊥AB,垂足为点D,则CD<CA,理由是__________________________.
垂线段最短
15.如图S5-11,∠B的同旁内角有____________________
______________________(写出一个即可).
16. 如图S5-12,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,若∠1=25°,则∠AED的度数为________________.
∠BCA(或∠BDC,
∠A,∠BCD)
50°
17.如图S5-13,D是AB上一点,CE∥BD,CB∥ED,EA⊥BA于点A,若∠ABC=38°,则∠AED= ________________.
52°
18.将一副三角板按如图S5-14所示的方式放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为________________.
75°
三、解答题(一)(本大题2小题,每小题8分,共16分)
19.如图S5-15,三角形ABC的顶点都在方格纸的格点上,将三角形ABC向右平移3格,再向上平移2格,请在图中画出平移后的三角形A′B′C′.
解:如答图S5-1,三角形A′B′C′即为所求.
20.如图S5-16,∠BAP+∠APD=180°,∠BAE=∠CPF.求证:AE∥PF.
证明:∵∠BAP+∠APD=180°,
∴AB∥CD.
∴∠BAP=∠CPA.
∵∠BAE=∠CPF,
∴∠PAE=∠APF.
∴AE∥PF.
四、解答题(二)(本大题2小题,每小题10分,共20分)
21.如图S5-17,在四边形ABCD中,延长AD至点E,已知AC平分∠DAB,∠DAB=70°,∠1=35°.
(1)求证:AB∥CD;
(2)求∠2的度数.
(2)解:∵AB∥CD,
∴∠2=∠DAB=70°.
22.如图S5-18,已知∠1=∠BDC,∠2+∠3=180°.
(1)求证:AD∥CE;
(2)若DA平分∠BDC,CE⊥AE于E,∠FAB=55°,求∠1的度数.
(1)证明:∵∠1=∠BDC,
∴AB∥CD.
∴∠2=∠ADC.
∵∠2+∠3=180°,
∴∠ADC+∠3=180°.
∴AD∥CE.
(2)解:∵CE⊥AE于E,
∴∠CEF=90°.
由(1)知AD∥CE,
∴∠DAF=∠CEF=90°.
∴∠ADC=∠2=∠DAF-∠FAB.
∵∠FAB=55°,
∴∠ADC=35°.
∵DA平分∠BDC,∠1=∠BDC,
∴∠1=∠BDC=2∠ADC=70°.
五、解答题(三)(本大题2小题,每小题12分,共24分)
23.如图S5-19,BE平分∠ABC交CD的延长线于E,∠ABC=2∠E,∠ADE=∠BCD.
(1)求证:AB∥EF;
(2)若AF平分∠BAD交DC的延长线于F,
判断AF与BE的位置关系,并说明理由.
(1)证明:∵BE平分∠ABC,
∴∠ABC=2∠ABE.
∵∠ABC=2∠E,
∴∠ABE=∠E.
∴AB∥EF.
(2)解:AF与BE的位置关系是垂直.理由如下:
∵∠ADE=∠BCD,
∴AD∥BC.
∴∠DAB+∠CBA=180°.
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABC=2∠ABE,∠BAD=2∠BAF.
∴2∠ABE+2∠BAF=180°.
∴∠ABE+∠BAF=90°.
∴∠AOB=90°.
∴AF⊥BE.
24.如图S5-20,直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.
(1)如图S5-20①,探究∠AME,∠MEN,∠ENC的数量关系,并说明理由;
(2)如图S5-20②,∠AME=30°,EF平分∠MEN,NP平分∠ENC,EQ∥NP,求∠FEQ的度数;
(3)如图S5-20③,点G为CD上一点,∠AMN=m∠EMN,∠GEK=m∠GEM,EH∥MN交AB于点H,直接写出∠GEK,∠BMN,∠GEH之间的数量关系.(用含m的式子表示)
解:(1)∠MEN=∠AME+∠ENC.理由如下:
如答图S5-2,过点E作l∥AB.
∵AB∥CD,∴l∥AB∥CD.
∴∠1=∠AME,∠2=∠ENC.
∵∠MEN=∠1+∠2,
∴∠MEN=∠AME+∠ENC.
谢 谢
第五章过关训练
一、选择题(本大题12小题,每小题3分,共36分)
1. 下列命题是真命题的( )
A. 两点之间直线最短
B. 如果ab>0,那么a>0,b>0
C. 内错角相等,两直线平行
D. 若|a|=1,则a=1
C
2. 下列网格中的图案,不能通过一个图案平移得到另一个图案的是( )
C
3. 下列说法正确的是( )
A. 图形的平移是指把图形沿水平方向移动
B. 平移前后图形的形状和大小都没有发生改变
C. “相等的角是对顶角”是一个真命题
D. “直角都相等”是一个假命题
B
4.如图S5-1,在平面内经过一点作已知直线m的平行线,可作平行线的条数有( )
A. 0条
B. 1条
C. 0条或1条
D. 无数条
C
5.如图S5-2,下列条件中不能判定a∥b的是( )
A. ∠1=∠2 B. ∠1=∠4
C. ∠1+∠2=180° D. ∠1+∠3=180°
C
6. 如图S5-3,直线a,b被直线c所截,则∠5的内错角是( )
A. ∠3
B. ∠2
C. ∠4
D. 不确定
B
7. 可以由图S5-4平移得到的图形是( )
C
8.如图S5-5,下列条件:①∠2+∠4=180°;②∠4=∠5;③∠1=∠6;④∠1=∠3;⑤∠6=∠2.其中能判断直线l1∥l2的有( )
A. 2个
B. 3个
C. 4个
D. 5个
B
9. 如图S5-6,AB∥CD,FE⊥DB,垂足为点E,若∠1=40°,则∠2的度数是( )
A. 60°
B. 50°
C. 40°
D. 30°
B
10. 如图S5-7,将一张含有30°角的三角形纸片的两个顶点叠放在长方形的两条对边上,若∠2=44°,则∠1的大小为( )
A. 14° B. 16°
C. 90°-α D. α-44°
A
11. 一把直尺和一块三角板ABC(含30°,60°角)摆放位置如图S5-8所示,直尺的一边与三角板的两直角边分别交于点D,E,另一边与三角板的两直角边分别交于点F,A,若∠CDE=40°,则∠BAF的大小为( )
A. 40°
B. 45°
C. 50°
D. 10°
D
C
二、填空题(本大题6小题,每小题4分,共24分)
13.将命题“任意两个直角都相等”改写成“如果……那么……”的形式:___________________________________
___________________________________________________.
如果两个角都是直角,那么这两
个角相等
14.如图S5-10,∠ACB=90°,CD⊥AB,垂足为点D,则CD<CA,理由是__________________________.
垂线段最短
15.如图S5-11,∠B的同旁内角有____________________
______________________(写出一个即可).
16. 如图S5-12,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,若∠1=25°,则∠AED的度数为________________.
∠BCA(或∠BDC,
∠A,∠BCD)
50°
17.如图S5-13,D是AB上一点,CE∥BD,CB∥ED,EA⊥BA于点A,若∠ABC=38°,则∠AED= ________________.
52°
18.将一副三角板按如图S5-14所示的方式放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为________________.
75°
三、解答题(一)(本大题2小题,每小题8分,共16分)
19.如图S5-15,三角形ABC的顶点都在方格纸的格点上,将三角形ABC向右平移3格,再向上平移2格,请在图中画出平移后的三角形A′B′C′.
解:如答图S5-1,三角形A′B′C′即为所求.
20.如图S5-16,∠BAP+∠APD=180°,∠BAE=∠CPF.求证:AE∥PF.
证明:∵∠BAP+∠APD=180°,
∴AB∥CD.
∴∠BAP=∠CPA.
∵∠BAE=∠CPF,
∴∠PAE=∠APF.
∴AE∥PF.
四、解答题(二)(本大题2小题,每小题10分,共20分)
21.如图S5-17,在四边形ABCD中,延长AD至点E,已知AC平分∠DAB,∠DAB=70°,∠1=35°.
(1)求证:AB∥CD;
(2)求∠2的度数.
(2)解:∵AB∥CD,
∴∠2=∠DAB=70°.
22.如图S5-18,已知∠1=∠BDC,∠2+∠3=180°.
(1)求证:AD∥CE;
(2)若DA平分∠BDC,CE⊥AE于E,∠FAB=55°,求∠1的度数.
(1)证明:∵∠1=∠BDC,
∴AB∥CD.
∴∠2=∠ADC.
∵∠2+∠3=180°,
∴∠ADC+∠3=180°.
∴AD∥CE.
(2)解:∵CE⊥AE于E,
∴∠CEF=90°.
由(1)知AD∥CE,
∴∠DAF=∠CEF=90°.
∴∠ADC=∠2=∠DAF-∠FAB.
∵∠FAB=55°,
∴∠ADC=35°.
∵DA平分∠BDC,∠1=∠BDC,
∴∠1=∠BDC=2∠ADC=70°.
五、解答题(三)(本大题2小题,每小题12分,共24分)
23.如图S5-19,BE平分∠ABC交CD的延长线于E,∠ABC=2∠E,∠ADE=∠BCD.
(1)求证:AB∥EF;
(2)若AF平分∠BAD交DC的延长线于F,
判断AF与BE的位置关系,并说明理由.
(1)证明:∵BE平分∠ABC,
∴∠ABC=2∠ABE.
∵∠ABC=2∠E,
∴∠ABE=∠E.
∴AB∥EF.
(2)解:AF与BE的位置关系是垂直.理由如下:
∵∠ADE=∠BCD,
∴AD∥BC.
∴∠DAB+∠CBA=180°.
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABC=2∠ABE,∠BAD=2∠BAF.
∴2∠ABE+2∠BAF=180°.
∴∠ABE+∠BAF=90°.
∴∠AOB=90°.
∴AF⊥BE.
24.如图S5-20,直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.
(1)如图S5-20①,探究∠AME,∠MEN,∠ENC的数量关系,并说明理由;
(2)如图S5-20②,∠AME=30°,EF平分∠MEN,NP平分∠ENC,EQ∥NP,求∠FEQ的度数;
(3)如图S5-20③,点G为CD上一点,∠AMN=m∠EMN,∠GEK=m∠GEM,EH∥MN交AB于点H,直接写出∠GEK,∠BMN,∠GEH之间的数量关系.(用含m的式子表示)
解:(1)∠MEN=∠AME+∠ENC.理由如下:
如答图S5-2,过点E作l∥AB.
∵AB∥CD,∴l∥AB∥CD.
∴∠1=∠AME,∠2=∠ENC.
∵∠MEN=∠1+∠2,
∴∠MEN=∠AME+∠ENC.
谢 谢
