2.4.3平面向量数量积的坐标表示
文档属性
| 名称 | 2.4.3平面向量数量积的坐标表示 |

|
|
| 格式 | zip | ||
| 文件大小 | 581.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-26 00:00:00 | ||
图片预览








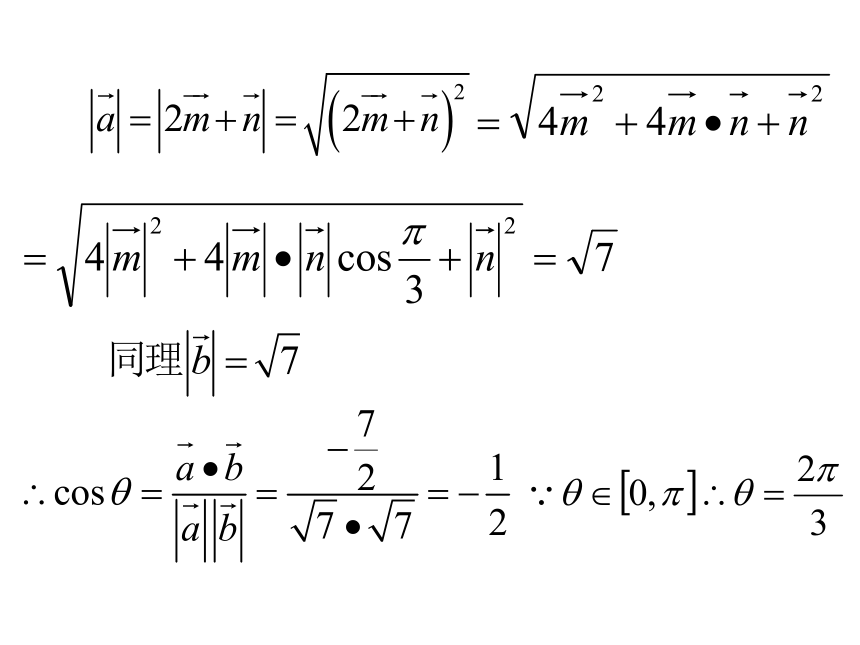
文档简介
课件23张PPT。一、平面向量数量积的定义:规定:零向量与任意向量的数量积为0.注意:平面向量数量积的几何意义:平面向量数量积的运算律:(1)交换律:(2)数乘结合律: (3)分配律: 数量积不满足下面的运算注意:平面向量数量积的重要性质:判断两个向量垂直的依据求向量模的依据求向量夹角的依据解:利用 求夹角:2.4.3平面向量数量积的坐标表示学习目标:(1)掌握向量数量积的坐标表达式, 会进行向量数量积的坐标运算;
(2)能运用数量积表示两个向量的夹角,计算向量的长度,会用数量积判断两个平面向量的垂直关系.一、平面向量数量积的坐标表示:二、向量的模和两点间距离公式:三、向量垂直和平行的坐标表示:(1)垂直:(2)平行:四、向量夹角公式的坐标表示:例2:已知A(1, 2),B(2, 3),C(?2, 5),
求证:△ABC是直角三角形 证明:即AB⊥AC, △ABC是直角三角形. 解:设所求向量为(x, y), 则例4:已知 =(1, 0), =(2, 1),当k为何实数时,向量k - 与 +3 (1)平行;(2)垂直(2)由向量垂直条件得7(k-2)-3=0(1)由向量平行条件得3(k-2)+7=0提高练习: 2、已知A(1,2)、B(4、0)、C(8,6)、D(5,8),
则四边形ABCD的形状是 .矩形 3、已知 = (1,2), = (-3,2),
若k +2 与 2 - 4 平行,则k = . - 1【总一总★成竹在胸】 (1)掌握平面向量数量积的坐标表示,即两个向量的数量积等于它们对应坐标的乘积之和; (2)要学会运用平面向量数量积的坐标表示解决有关长度、角度及垂直问题.
(2)能运用数量积表示两个向量的夹角,计算向量的长度,会用数量积判断两个平面向量的垂直关系.一、平面向量数量积的坐标表示:二、向量的模和两点间距离公式:三、向量垂直和平行的坐标表示:(1)垂直:(2)平行:四、向量夹角公式的坐标表示:例2:已知A(1, 2),B(2, 3),C(?2, 5),
求证:△ABC是直角三角形 证明:即AB⊥AC, △ABC是直角三角形. 解:设所求向量为(x, y), 则例4:已知 =(1, 0), =(2, 1),当k为何实数时,向量k - 与 +3 (1)平行;(2)垂直(2)由向量垂直条件得7(k-2)-3=0(1)由向量平行条件得3(k-2)+7=0提高练习: 2、已知A(1,2)、B(4、0)、C(8,6)、D(5,8),
则四边形ABCD的形状是 .矩形 3、已知 = (1,2), = (-3,2),
若k +2 与 2 - 4 平行,则k = . - 1【总一总★成竹在胸】 (1)掌握平面向量数量积的坐标表示,即两个向量的数量积等于它们对应坐标的乘积之和; (2)要学会运用平面向量数量积的坐标表示解决有关长度、角度及垂直问题.
