线性相关与线性回归方程

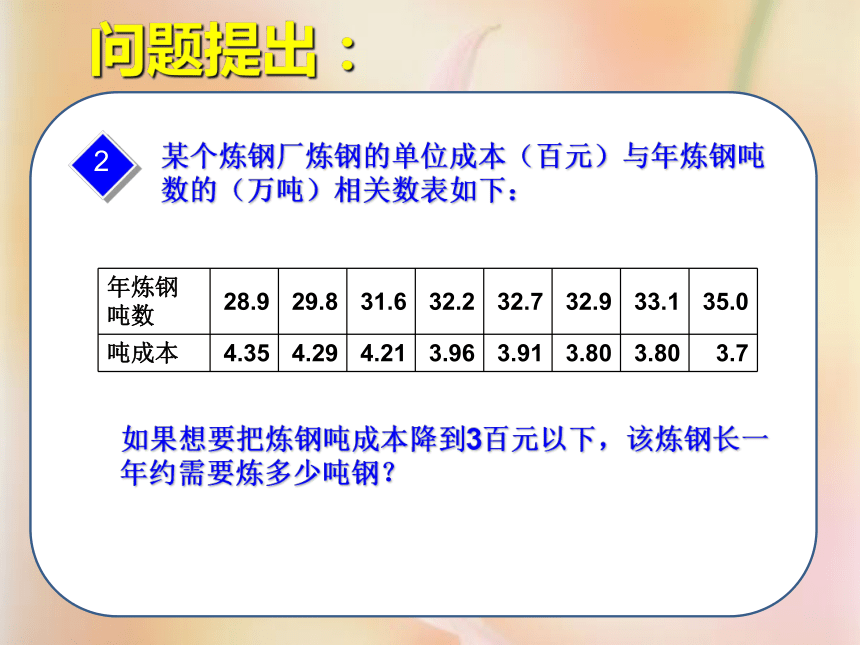
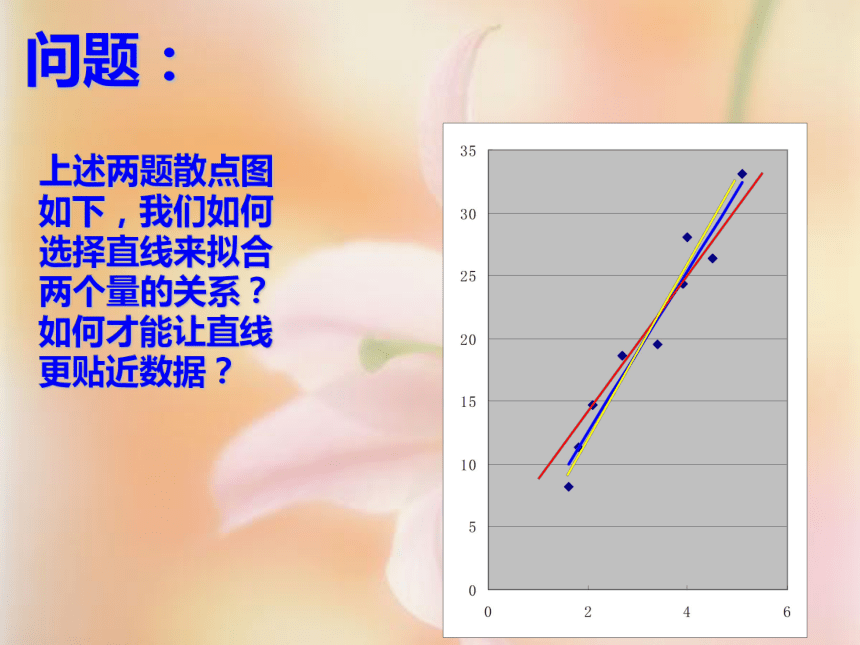
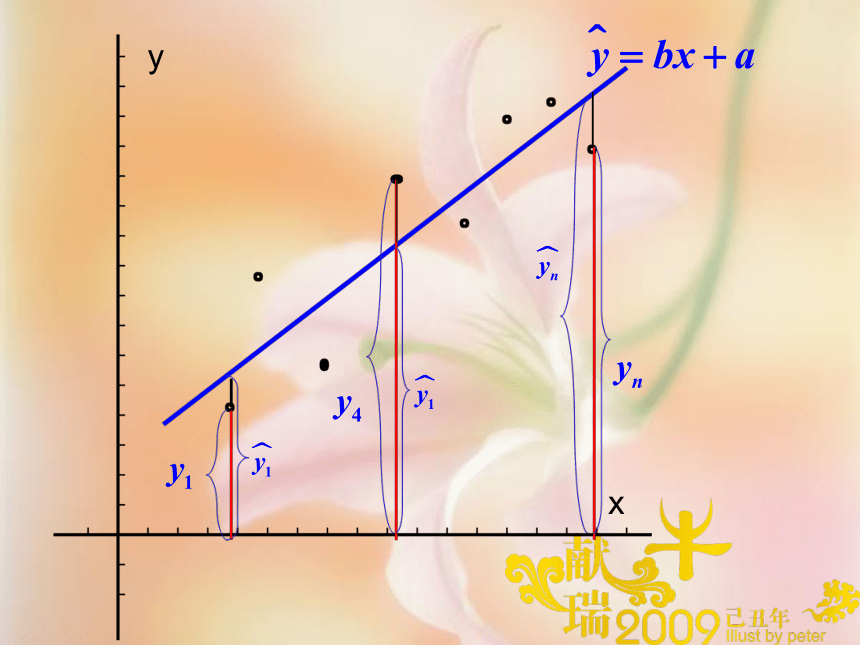
课件28张PPT。线性相关与线性回归方程问题提出：一种化妆品过去10年中在某市的销售收入（单位：亿元）与该市居民年人均收入（单位：万元）如下表：明年该市年人均收入要达到6万元人民币，如果你是该化妆品的总代理，你能估计该化妆品在该市的销售收入吗？问题提出：某个炼钢厂炼钢的单位成本（百元）与年炼钢吨数的（万吨）相关数表如下：如果想要把炼钢吨成本降到3百元以下，该炼钢长一年约需要炼多少吨钢？2问题：上述两题散点图如下，我们如何选择直线来拟合两个量的关系？如何才能让直线更贴近数据？问题：一般地，设x与y是具有相关关系的两个变量，且相应于n个观测值的n个点大致分布在一条直线的附近，我们来求在整体上与这n个点最“接近”的一条直线．那么“接近”的标准是什么？yx 设所求的直线的方程为 ＝bx＋a，(在一般统计书中，习惯用b表示一次项系数，用a表示常数项，这正好与我们表示一次函数的习惯相反)其中a，b是待确定的参数．于是，当变量x取一组数值xi（i=1，2，……，n）时，相应地 =bxi＋a（i＝1，2，……，n）yx 于是得到各个偏差yi－ i=yi－(bxi+a) （i＝1，2，……，n）． 容易看到，上面各个偏差的符号可能有正有负，如果将它们相加会造成相互抵消，因此它们的和不能代表n个点与相应直线在整体上的接近程度．为了解决这一问题，我们采用n个偏差的平方和，即 Q=(y1－bx1－a)2＋(y2－bx2－a)2＋……＋(yn－bxn－a)21.最小二乘法 Q=(y1－bx1－a)2＋(y2－bx2－a)2＋……＋(yn－bxn－a)2 来表示n个点与相应直线在整体上的接近程度． 于是我们的问题是，如何求得系数a，b，使Q取得最小值． 这个式子展开后，是一个关于a，b的二次多项式．利用配方法，可以导出使Q取得最小值的a，b的求值公式（详细推导过程不做要求）.
这里，我们将所得到的方程叫做回归直线方程，相应的直线叫做回归直线，而对两个变量所进行的上述统计分析叫做线性回归分析．我们看到，求出了这种具有两个变量的回归直线后，就可以根据其部分观测值，获得对这两个变量之间整体关系的了解．　　“回归”这个名词是高尔登在研究遗传现象时提出的．他发现：下一代身高与父母身高呈相关关系，下一代的身高有向中心回归的趋势．后人就把反映相关变量之间的关系的方程通称为“回归方程”，对两个变量所进行的统计分析叫做回归分析． 特别提醒：2.典型例题：一种化妆品过去10年中在某市的销售收入（单位：亿元）与该市居民年人均收入（单位：万元）如下表：（1）画出散点图
（2）求出回归方程
（3）明年该市年人均收入要达到6万元人民币，如果你是该化妆品的总代理，你能估计该化妆品在该市的销售收入吗？解：（1）画出散点图如图（2）回归直线方程= 6.4287x - 0.3307（3）x=6时，＝38.2亿元解2：设回归方程典型例题：某个炼钢厂炼钢的单位成本（百元）与年炼钢吨数的（万吨）相关数表如下：（1）画出散点图
（2）求出回归方程
（3）如果想要把炼钢吨成本降到3百元以下，该炼钢长一年约需要炼多少吨钢？3.小结：运用回归分析的方法来分析、处理数据的步骤是：
　　
①收集数据，并制成表格；
②画出数据的散点图；
③利用散点图直观认识变量间的相关关系；
④运用科学计算器、Excel表格等现代信息技术手
　段求解回归方程；
⑤通过研究回归方程，提取有用信息，作出比较
　可靠的趋势预测．补充练习1.有时候，一些东西吃起来口味越好，对我们的身体越有害，下表给出了不同类型的某种类型食品的数据，第一列表示此种所含热量的百分比，第二列数据表示由一些美食家以百分制给出的此种食品口味的评价：（1）做出这些数据的散点图
（2）作出回归直线
（3）关于两个变量之间关系，你能得出什么样的结论？
（4）对于这种食品为什么人们更喜欢吃位于回归直线上方的食品而不是下方的？补充练习2.一个车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了10次试验，收集数据如下：（1）做出这些数据的散点图
（2）作出回归直线
（3）关于加工零件的个数与加工时间，你能得出什么结论？补充练习3.3、给出施化肥量对水稻产量影响的试验数据：(1)画出上表的散点图;
(2)求出回归直线并且画出图形 作业：
课本P86 A（4）
P87 B（1）