人教版物理八年级下册同步训练 12.3机械效率(WORD版,含答案与解析)
文档属性
| 名称 | 人教版物理八年级下册同步训练 12.3机械效率(WORD版,含答案与解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 245.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-05 00:00:00 | ||
图片预览


文档简介
12.3机械效率
一.选择题(共13小题)
1.如图所示,斜面高为1m,长为4m,用沿斜面向上大小为75N的拉力F,将重为200N的木箱由斜面底端匀速缓慢拉到顶端,下列关于做功的判断正确的是( )
A.木箱克服重力做功大小为300J
B.木箱受到的合力做功的大小为300J
C.木箱受到斜面的支持力做功大小为200J
D.木箱克服斜面摩擦力做功大小为100J
2.甲吊车比乙吊车的机械效率高,当它们分别把相同质量的物体匀速提升相同高度时,则( )
A.乙吊车做的总功较多
B.乙吊车做的有用功较多
C.甲吊车做的有用功较多
D.甲、乙两吊车做的总功相同
3.一滑轮组经改进提高了效率,把同一物体匀速升高同样的高度,改进后和改进前相比较( )
A.做的有用功减少了 B.做的有用功增加了
C.做的额外功增加了 D.做的总功减少了
4.下列关于机械效率的说法中正确的是( )
A.越省力的机械,机械效率越高
B.所做有用功越多的机械,机械效率越高
C.做功相等的情况下,额外功越少的机械,机械效率越高
D.做功越快的机械,机械效率越高
5.关于机械效率,下列说法正确的是( )
A.机械效率大的机器功率大
B.最优秀的机器的机械效率可达到100%
C.所做有用功越多,机械效率越高
D.有用功永远小于总功,所以机械效率小于1
6.如图所示,小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼,用甲滑轮所做的总功为W1,机械效率为η1;用乙滑轮所做的总功为W2,机械效率为η2.若不计绳重与摩擦,则( )
A.W1=W2 η1=η2 B.W1=W2 η1<η2
C.W1<W2 η1>η2 D.W1>W2 η1<η2
7.如图所示斜面,斜面AB、AC的粗糙程度相同,把同一物体沿斜面BA和CA分别匀速拉到顶端A,若沿斜面的拉力F1=F2,斜面两边的机械效率分别为ηB、ηC,斜面两边的摩擦力分别为fB、fC,则下列判断正确的( )
A.ηB<ηC,fB<fC B.ηB>ηC,fB=fC
C.ηB<ηC,fB>fC D.ηB>ηC,fB<fC
8.如图甲,邻居大叔正吃力地把一重物搬上高台,放学回家的小明看见后急忙前去帮忙,他找来一块木板,搭成图乙所示的斜面,结果非常轻松的把同样的重物推到了高台上。关于这两种方法,下列说法正确的是( )
A.甲种情况下更省力 B.乙种情况的机械效率高
C.两人做同样多的有用功 D.小明做功的功率要大些
9.两台机械完成的有用功之比W1:W2=4:7,它们的机械效率分别为η1=60%,η2=75%,则两台机械所做总功之比为( )
A.5:7 B.7:5 C.16:35 D.35:16
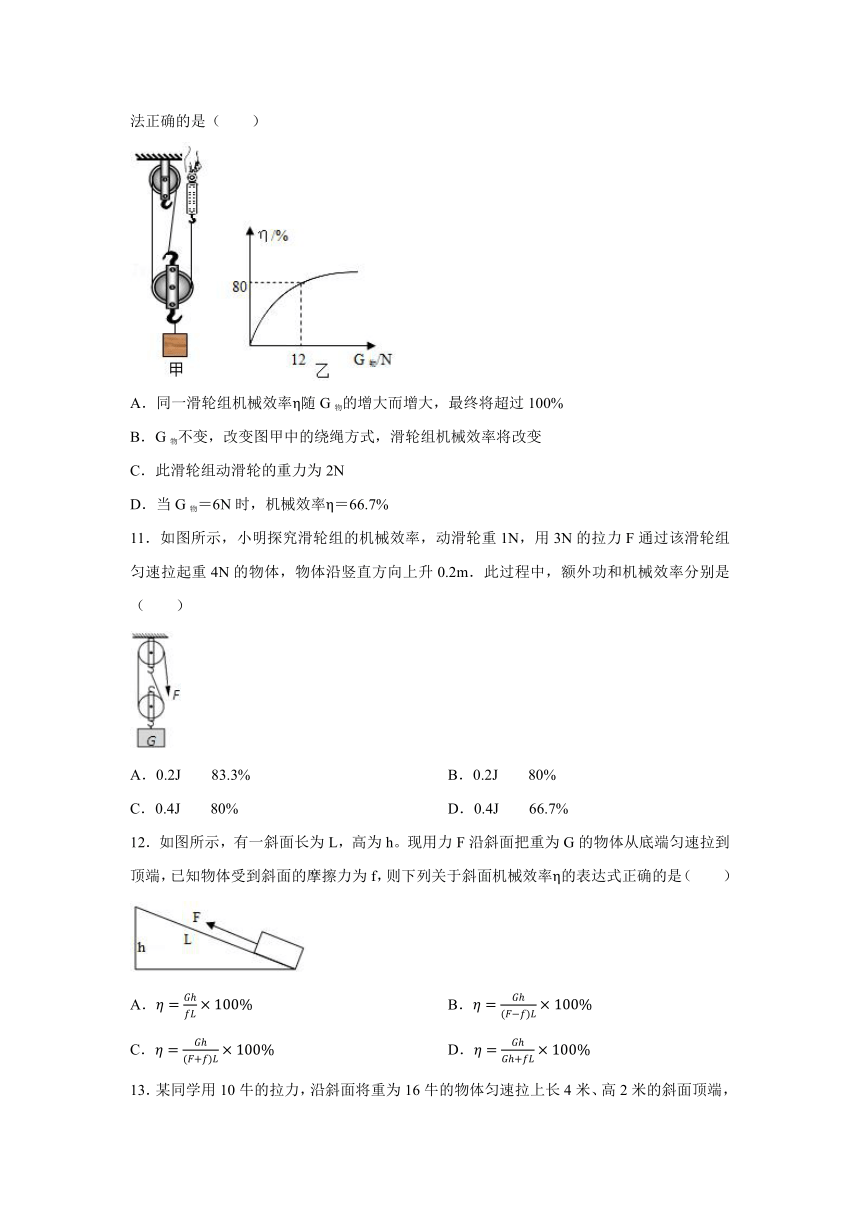
10.用如图甲所示的装置来探究滑轮组的机械效率η与物重G物的关系,改变G物,竖直向上匀速拉动弹簧测力计,计算并绘出η与G物关系如图乙所示,若不计绳重和摩擦,则下列说法正确的是( )
A.同一滑轮组机械效率η随G物的增大而增大,最终将超过100%
B.G物不变,改变图甲中的绕绳方式,滑轮组机械效率将改变
C.此滑轮组动滑轮的重力为2N
D.当G物=6N时,机械效率η=66.7%
11.如图所示,小明探究滑轮组的机械效率,动滑轮重1N,用3N的拉力F通过该滑轮组匀速拉起重4N的物体,物体沿竖直方向上升0.2m.此过程中,额外功和机械效率分别是( )
A.0.2J 83.3% B.0.2J 80%
C.0.4J 80% D.0.4J 66.7%
12.如图所示,有一斜面长为L,高为h。现用力F沿斜面把重为G的物体从底端匀速拉到顶端,已知物体受到斜面的摩擦力为f,则下列关于斜面机械效率η的表达式正确的是( )
A. B.
C. D.
13.某同学用10牛的拉力,沿斜面将重为16牛的物体匀速拉上长4米、高2米的斜面顶端,则该斜面的机械效率及斜面对物体的摩擦力分别为( )
A.0.5,8牛 B.0.8,2牛 C.0.8,8牛 D.0.5,2牛
二.实验探究题(共4小题)
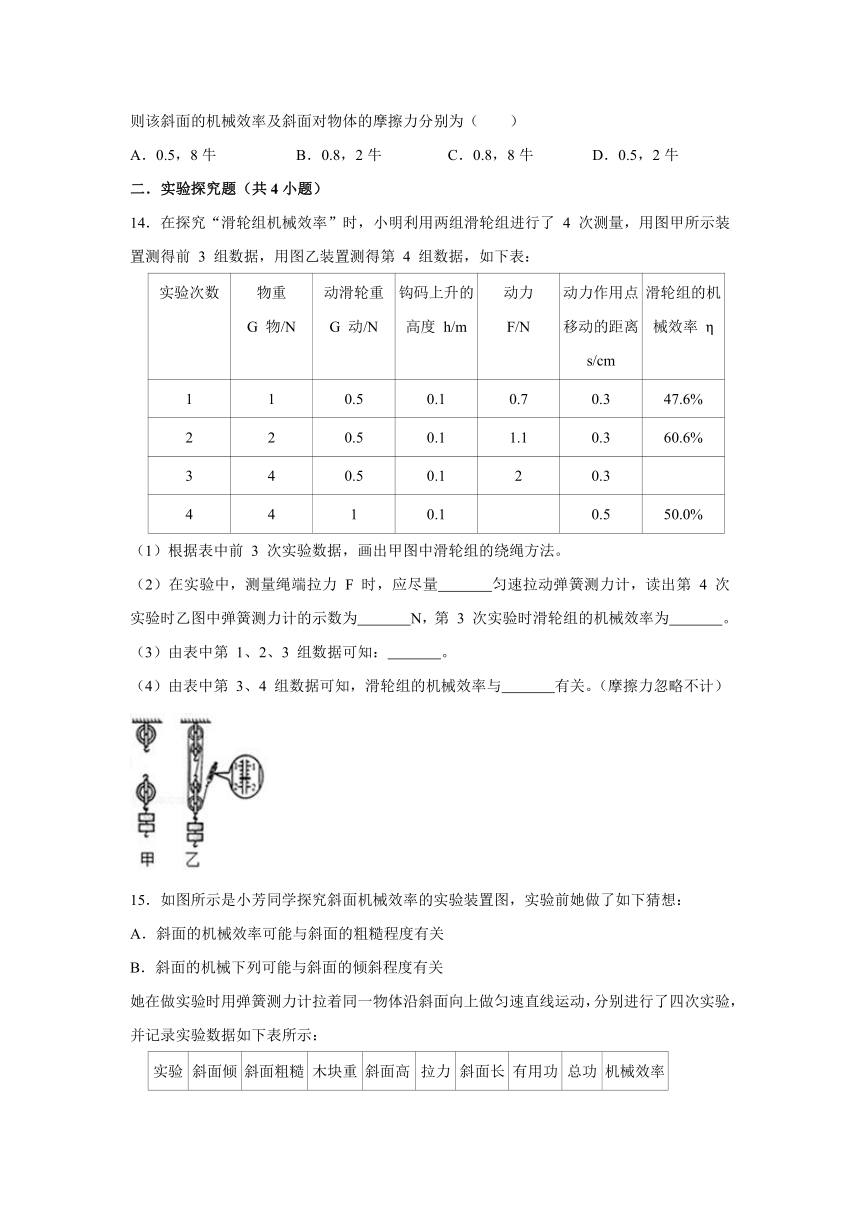
14.在探究“滑轮组机械效率”时,小明利用两组滑轮组进行了 4 次测量,用图甲所示装置测得前 3 组数据,用图乙装置测得第 4 组数据,如下表:
实验次数 物重 G 物/N 动滑轮重 G 动/N 钩码上升的高度 h/m 动力 F/N 动力作用点移动的距离 s/cm 滑轮组的机械效率 η
1 1 0.5 0.1 0.7 0.3 47.6%
2 2 0.5 0.1 1.1 0.3 60.6%
3 4 0.5 0.1 2 0.3
4 4 1 0.1 0.5 50.0%
(1)根据表中前 3 次实验数据,画出甲图中滑轮组的绕绳方法。
(2)在实验中,测量绳端拉力 F 时,应尽量 匀速拉动弹簧测力计,读出第 4 次实验时乙图中弹簧测力计的示数为 N,第 3 次实验时滑轮组的机械效率为 。
(3)由表中第 1、2、3 组数据可知: 。
(4)由表中第 3、4 组数据可知,滑轮组的机械效率与 有关。(摩擦力忽略不计)
15.如图所示是小芳同学探究斜面机械效率的实验装置图,实验前她做了如下猜想:
A.斜面的机械效率可能与斜面的粗糙程度有关
B.斜面的机械下列可能与斜面的倾斜程度有关
她在做实验时用弹簧测力计拉着同一物体沿斜面向上做匀速直线运动,分别进行了四次实验,并记录实验数据如下表所示:
实验次数 斜面倾斜程度 斜面粗糙 程度 木块重量G/N 斜面高h/m 拉力F/N 斜面长 s/m 有用功 W有/J 总功W总/J 机械效率 η
1 较缓 木板表面 2 0.1 0.6 0.5 0.2 0.3 67%
2 较陡 木板表面 2 0.2 1 0.5 0.4 0.5 80%
3 最陡 木板表面 2 0.3 1.4 0.5 0.6 0.7 86%
4 最陡 毛巾表面 2 0.3 1.6 0.5 0.6 0.8
(1)将表中所缺的数据补充完整。
(3)比较 两次实验可知猜想A是正确的。
(3)比较1、2、3次实验得到的结论是:当粗糙程度相同时,斜面越陡机械效率 。
(4)通过分析实验数据,还可以得出当斜面粗糙程度和高度都相同时,斜面越长越 (选填“省力”或“费力”)。
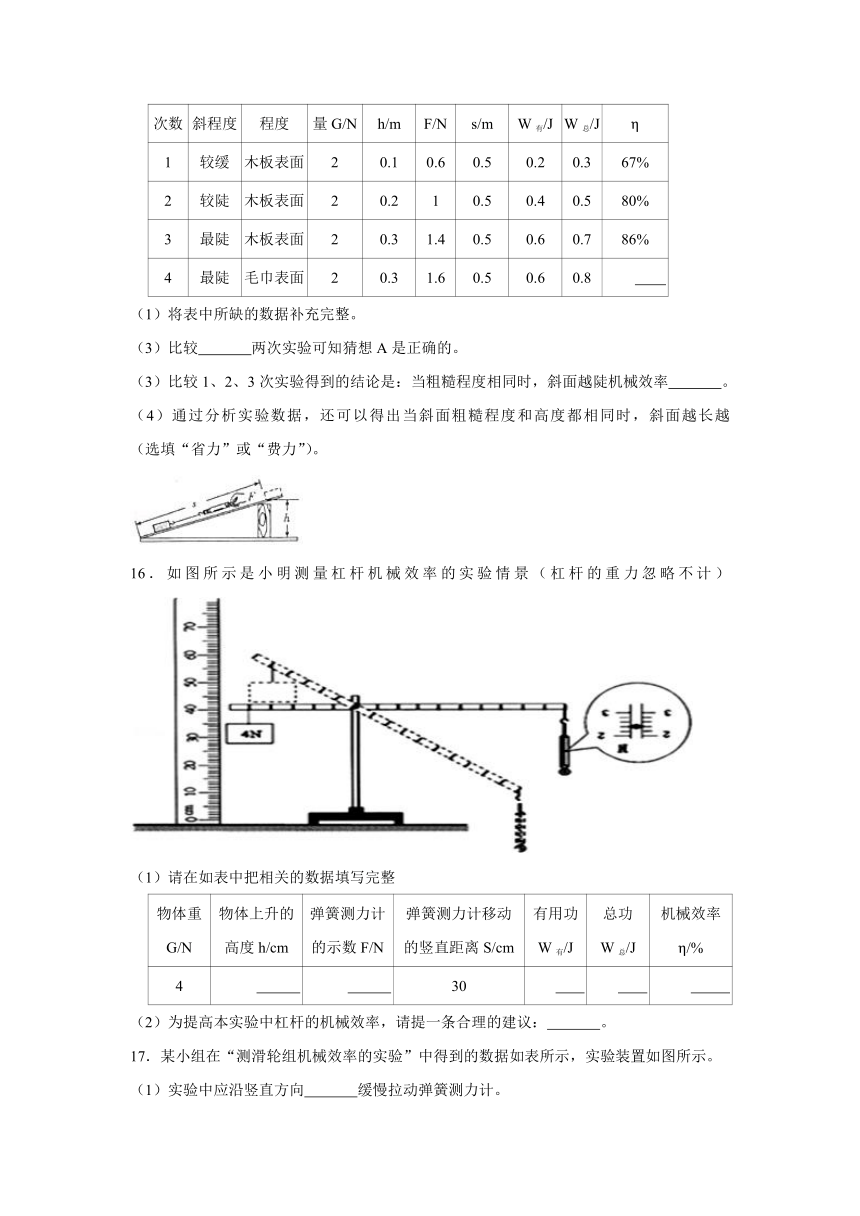
16.如图所示是小明测量杠杆机械效率的实验情景(杠杆的重力忽略不计)
(1)请在如表中把相关的数据填写完整
物体重 G/N 物体上升的 高度h/cm 弹簧测力计 的示数F/N 弹簧测力计移动 的竖直距离S/cm 有用功 W有/J 总功 W总/J 机械效率 η/%
4 30
(2)为提高本实验中杠杆的机械效率,请提一条合理的建议: 。
17.某小组在“测滑轮组机械效率的实验”中得到的数据如表所示,实验装置如图所示。
(1)实验中应沿竖直方向 缓慢拉动弹簧测力计。
(2)小组同学发现实验过程中边拉动边读数,弹簧测力计示数不稳定,应该静止读数。你认为他的想法 (选填“正确”或“不正确”),因为他没有考虑到 对滑轮组机械效率的影响。
实验次数 钩码重G/N 钩码上升高 度h/m 绳端拉力 F/N 绳端移动距离 s/m 机械 效率η
1 4 0.1 2.7 0.2 74%
2 4 0.1 1.8 0.3 74%
3 8 0.1 3.1 0.3 86%
4 8 0.1 2.5
(3)用丁图装置进行实验,得出表中第4次实验数据,请将表中的两个数据填写完整。
(4)通过比较 (填实验次数的序号)两次实验数据可得出结论:使用同一滑轮组提升同一重物时,滑轮组的机械效率与绳子段数无关。
(5)通过比较 (填实验次数的序号)两次实验数据可得出结论:同一滑轮组提升重物时,物重越大,滑轮组机械效率越高。
(6)通过比较3、4两次实验数据可得出结论: 。
三.计算题(共4小题)
18.小明利用如图所示的滑轮组提升重物,不计绳重和轮、轴间摩擦.当匀速提起重为480N的物体时,绳端的拉力F为200N。求:
(1)此过程中,滑轮组的机械效率为多大?
(2)动滑轮有多重?
(3)绳子能承受的最大拉力为400N,该滑轮组的最大机械效率为多大?
19.一辆质量是3.5t的汽车不慎陷入泥泞地面,汽车司机组织人们用如图所示的滑轮组将汽车拖出。已知整个过程中,水平拉力F是1000N,汽车沿水平方向匀速移动了1m,滑轮组的机械效率为90%.求:
(1)拉力F做的总功。
(2)有用功为多大。
(3)汽车受到的阻力大小。
20.小明在探究利用杠杆做功的实践活动中,把重G为285N的重物挂在杠杆的中点,用手竖直提起棒的一端,使物体缓慢匀速提升,如图所示。
(1)若不计杠杆自身重力和摩擦,求拉力F的大小?
(2)如杠杆是一根重为15N、质量均匀的硬棒,小明利用此杠杆2s内将重物提升了0.1m,则小明使用杠杆所做的有用功是多大?机械效率是多大?
21.如图所示,为了清洗水池,某工人重600N,站在池外地面上,用100N的拉力向下匀速拉动绳子提起一浸没在水中体积为1.2×10﹣2m3、重360N的石块(石块始终浸没在水中,且忽略水对石块的阻力,ρ水=1×103kg/m3,g=10N/kg)求:
(1)石块浸没在水中时受到的浮力;
(2)将石块提升到石块上表面与水面齐平的过程中滑轮组的机械效率。
(3)若将石块从刚露出水面到完全露出水面的过程中也是匀速提升,试分析在此过程中,石块所受浮力和滑轮组机械效率的变化情况。
参考答案
一.选择题(共13小题)
1.【解析】解:A、由题意知,木箱的重力G=200N,h=1m,
则克服重力做功:W有用=Gh=200N×1m=200J,故A错误;
B、木箱沿斜面匀速缓慢运动,处于平衡状态,则木箱所受合力为零,所以合力做功大小为0J,故B错误;
C、木箱移动方向与支持力方向垂直,所以斜面的支持力做功为0J,故C错误;
D、拉力F做的功:W总=FL=75N×4m=300J;
则克服摩擦力做功:W额=W总﹣W有用=300J﹣200J=100J,故D正确。
【答案】D。
2.【解析】解:
BC、根据公式W有用=Gh=mgh可知甲、乙吊车做的有用功相同,BC选项错误;
AD、两辆吊车做的有用功相同,乙的效率较低,所以乙吊车做总功较多,A选项正确,D选项错误。
【答案】A。
3.【解析】解:把同一物体匀速提升同样的高度,
由W=Gh可知:利用滑轮组做的有用功相同;
滑轮组改进后提高机械效率,
由η100%可知:改装后滑轮组的机械效率提高了,所以做的总功减少;
由W总=W有+W额知:改装后利用滑轮组做的额外功减少;
由上述分析得出,A、B、C错,D正确。
【答案】D。
4.【解析】解:
A、机械效率是指有用功占总功的百分比,与是否省力没有必然的联系,故A说法错误;
B、效率指有用功占总功的比值,有用功多,如果额外功更多,则效率不一定高,故B说法错误;
C、做功相等的情况下,额外功越少的机械,有用功占的越多,所以机械效率越高,故C说法正确;
D、机械做功越快,表示功率越大,机械效率与功率间没有必然联系,故D说法错误。
【答案】C。
5.【解析】解:
A、有用功与总功的比值叫机械效率,而功率是功与时间的比值,二者没有必然的联系,故A错误;
B、使用机械时,不可避免地要做额外功,所以总功一定大于有用功,即机械效率不可能达到100%,故B错误;
C、有用功与总功的比值叫机械效率,只知道有用功多,机械效率不一定高,故C错误;
D、使用机械时,不可避免地要做额外功,有用功永远小于总功,所以机械效率一定小于1,故D正确。
【答案】D。
6.【解析】解:
(1)因为小明分别用甲、乙两滑轮把同一袋沙从地面提到二楼,所以两种情况的有用功相同;
(2)当有用功一定时,乙中所做的总功为对一袋沙所做的功,利用机械时做的额外功越少,则总功就越少,机械效率就越高;
又因为甲是动滑轮,甲中所做的总功还要加上对动滑轮所做的功,利用甲滑轮做的额外功多,则总功越多,机械效率越低。即W1>W2,η1<η2。
【答案】D。
7.【解析】解:(1)由题知,同一物体提升的高度h相同,由W有=Gh可知,有用功相同,
因AB<AC,且拉力相同,
所以,由W总=Fs可知,F2做的总功多,
由η100%可知,右边斜面的机械效率低,即ηB>ηC,故AC错误;
(2)影响滑动摩擦力大小的因素有两个:压力大小和接触面的粗糙程度,
物体分别沿斜面BA和CA运动,接触面的粗糙程度相同,斜面越陡,则压力越小,滑动摩擦力越小,由图知BA斜面更陡一些,所以fB<fC,故B错误、D正确。
【答案】D。
8.【解析】解:
A、斜面是一种省力机械,利用斜面将物体推上高台可更省力,所以,甲种情况费力,故A错误;
B、由于乙中情况需要克服摩擦做功,所以乙种情况下的机械效率小。故B错误;
C、这两种方法,都把重物推到了高台上,两人做同样多的有用功,克服重力做功相同,故C正确;
D、功率等于功与时间的比值,由于题中没有给出时间,不能确定哪个做功的功率大。故D错误。
【答案】C。
9.【解析】解:由η1=60%,η2=75%可知:η1:η2=4:5.而η,所以W总。
有用功W1:W2=4:7,则总功W1总:W2总:5:7,故选A。
10.【解析】解:A、使用滑轮组时,克服物重的同时,不可避免地要克服动滑轮重、摩擦和绳子重做额外功,所以总功一定大于有用功;由公式η知:机械效率一定小于1,即同一滑轮组机械效率η随G物的增大而增大,但最终不能超过100%,故A错误;
B、G物不变,改变图甲中的绕绳方式,如图所示,
因为此图与题干中甲图将同一物体匀速提高相同的高度,所以所做的有用功相同,
忽略绳重及摩擦时,额外功:W额=G轮h,即额外功W额相同,
又因为W总=W有+W额,所以总功相同,
由η可知,两装置的机械效率相同,即η1=η2.故B错误;
C、由图可知,G=12N,此时η=80%,
则η,即80%,
解得G动=3N,故C错误;
D、G物=6N时,机械效率η100%100%100%100%≈66.7%.故D正确。
【答案】D。
11.【解析】解:
有用功为W有用=Gh=4N×0.2m=0.8J;
绳子拉下的长度为s=2h=2×0.2m=0.4m,
拉力做的总功为W总=Fs=3N×0.4m=1.2J。
额外功为W额=W总﹣W有用=1.2J﹣0.8J=0.4J;
机械效率为η100%≈66.7%。
【答案】D。
12.【解析】解:
斜面的高为h,物体的重力为G,
则有用功为:W有用=Gh,
又因为斜面长为L,拉力为F,
所以拉力所做的总功为:W总=FL,
则斜面的机械效率为:η100%100%;
而物体受到斜面的摩擦力为f,
则克服摩擦力做的额外功为:W额外=fL,
所以总功为:W总=W有用+W额外=Gh+fL,
则斜面的机械效率为:η100%100%,故ABC错误,D正确。
【答案】D。
13.【解析】解:W有用=Gh=16N×2m=32J,
W总=Fs=10N×4m=40J,
η80%=0.8;
∵W总=W有用+W额,
∴W额=W总﹣W有用=40J﹣32J=8J,
∵W额=fs,
∴f2N。
【答案】B。
二.实验探究题(共4小题)
14.【解析】解:
(1)表中前 3 次实验数据,根据s=nh可得,绳子的有效段数:n3;
根据偶定奇动原则,绳子应系在动滑轮的上面挂钩上,由此绕线,如下所示:
(2)在实验中,测量绳端拉力F 时,应尽量竖直向上匀速拉动弹簧测力计,此时系统处于平衡状态,测力计示数才等于拉力的大小;
图乙中测力计分度值为0.2N,乙图中弹簧测力计的示数为 1.6N,
第 3 次实验时滑轮组的机械效率为:
η100%100%≈66.7%。
(3)图甲所示装置测得前 3 组数据,由表中第 1、2、3 组数据可知:使用同一滑轮组,提升的物体越重,机械效率越大;
(4)由题知,小明利用两组滑轮组进行了 4 次测量,用图甲所示装置测得前 3 组数据,则用图乙所示装置测得第4组数据;
由表中第 3、4 组数据可知,提升物体的重力相同,第3次实验要克服1个动滑轮重(0.5N)做额外功,而第4次实验要克服2个动滑轮重(1N)做额外功,两次的机械效率不同,说明滑轮组的机械效率与动滑轮重有关。
【答案】(1)如上所示;(2)竖直向上;1.6;66.7%;(3)同一滑轮组,提升的物重越大,机械效率越大;(4)动滑轮重。
15.【解析】解:
(1)由表中数据,机械效率η100%=75%;
(2)要验证斜面的机械效率可能与斜面的粗糙程度有关,要控制斜面倾斜程度相同,只改变斜面的粗糙程度,故由表中3、4两次实验数据可知,在斜面粗糙程度不同而斜面的倾斜程度相同时,斜面的效率不同,由此可知,斜面的机械效率与斜面的粗糙程度有关,故猜想A正确;
(3)由表中第1、2、3此实验数据可知,当斜面粗糙程度相同时,斜面越陡,机械效率越高;
(4)分析表中数据可知,斜面的长度相同,都是0.5m,高度越高,拉力F越大,即:斜面越陡越费力,越缓越省力。
由此可推知,当斜面的高度相同时,斜面越长,则倾斜程度越缓,此时会越省力。
【答案】(1)75%;(2)3、4;(3)越高;(4)省力。
16.【解析】解:(1)从实验的物体的重力标识为4N,测力计指针对应的刻度是2.4N即拉力的大小;
物体升高的高度以物体上边沿为参照点,位置高度变化为由35cm到50cm,共移动15cm;
测力计竖直移动的距离以杠杆右端为参照点,位置高度变化为由43cm到13cm,共移动30cm;
并将读数记录在表格中,则:
W有=Gh=4N×0.15m=0.6J;
W总=FS=2.4N×0.3m=0.72J;
所以η100%100%≈83.3%。
(2)提高机械效率的方法根本途径是:减小机械的重力和机械之间的摩擦。使用杠杆时,杠杆只是转动,杠杆的重力产生的额外功很少,主要是杠杆的摩擦,所以选择支点灵活的杠杆或在支点所在轴处加润滑油等减小摩擦的方法都可以提高机械效率。
【答案】(1)15;2.4;0.6;0.72;83.3;(2)选择支点灵活的杠杆或在支点所在轴处加润滑油。
17.【解析】解:
(1)在测量滑轮组机械效率的实验中,应竖直向上缓慢匀速拉动弹簧测力计,这样保证滑轮组处于平衡状态,且便于读出测力计的示数;
(2)若在静止时读数,测力计没有测出绳子与滑轮间的摩擦,测得的拉力偏小,他的想法不正确;原因是没有考虑到摩擦对滑轮组机械效率的影响。
(3)用丁图进行实验,可以看出绳子段数为4段,则绳端移动距离:
s=nh=4×0.1m=0.4m,
滑轮组的机械效率:
η100%=80%;
如下表所示:
实验次数 钩码重G/N 钩码上升高 度h/m 绳端拉力 F/N 绳端移动距离 s/m 机械 效率η
1 4 0.1 2.7 0.2 74%
2 4 0.1 1.8 0.3 74%
3 8 0.1 3.1 0.3 86%
4 8 0.1 2.5 0.4 80%
(4)在比较滑轮组的机械效率与绳子段数的关系时,应保持滑轮组相同、物重相同,而绳子绕法不同,因此比较1和2两次实验即可得出结论;
(5)研究同一滑轮组提升重物时,滑轮组机械效率与提升物体的重力的关系时,要控制其它因素相同,只改变提升物体的重力,故通过比较2、3可得出滑轮组机械效率与物重的关系;
(6)通过比较3、4两次实验数据知,提升物体的重力相同,而丙中动滑轮的重力小于丁中动滑轮的重力和,丙的机械效率较大,故可得出的结论:不同滑轮组提升相同重物时,动滑轮越轻,滑轮组机械效率越高(不同滑轮组提升相同重物时,动滑轮越重,滑轮组机械效率越低)。
【答案】
(1)匀速;(2)不正确;摩擦;(3)如上表所示;(4)1、2;(5)2、3;(6)不同滑轮组提升相同重物时,动滑轮越轻,滑轮组机械效率越高(不同滑轮组提升相同重物时,动滑轮越重,滑轮组机械效率越低)。
三.计算题(共4小题)
18.【解析】解:(1)由图可知,滑轮组绳子的有效股数n=3,则滑轮组的机械效率:
η100%100%100%100%100%=80%;
(2)不计绳重和轮、轴间摩擦,由F(G+G动)可得,动滑轮的重力:
G动=nF﹣G=3×200N﹣480N=120N;
(3)绳子能承受的最大拉力为400N,则提升物体的最大重力:
G大=nF大﹣G动=3×400N﹣120N=1080N,
该滑轮组的最大机械效率:
η大100%100%100%100%100%=90%。
答:(1)此过程中,滑轮组的机械效率为80%;
(2)动滑轮的重力为120N;
(3)绳子能承受的最大拉力为400N,该滑轮组的最大机械效率为90%。
19.【解析】解:
(1)由图知,n=3,
拉力端移动的距离:s=3s物=3×1m=3m,
拉力F做的总功:W总=Fs=1000N×3m=3×103J;
(2)由η可得有用功:
W有用=W总η=3×103J×90%=2.7×103J。
(3)因为W有用=fs物,
则汽车受到的阻力:
f2.7×103N。
答:(1)拉力F做的总功为3×103J;
(2)有用功为2.7×103J;
(3)汽车受到的阻力大小为2.7×103N。
20.【解析】解:(1)由于重物挂在杠杆的中点,用手竖直提起棒的一端,则L1=2L2,若不计杠杆自身重力和摩擦,由杠杆原理FL1=GL2可得:
F142.5N。
(2)所做的有用功为:W有用=Gh=285N×0.1m=28.5J,
所做的额外功为:W额外=G杆h=15N×0.1m=1.5J,
总功为:W总=W有用+W额外=28.5J+1.5J=30J,
机械效率为:η100%100%=95%。
答:(1)若不计杠杆自身重力和摩擦,拉力F是142.5N。
(2)小明使用杠杆所做的有用功为28.5J.机械效率是95%。
21.【解析】解:
(1)石块浸没在水中,V排=V=1.2×10﹣2m3,
所受浮力:
F浮=ρ水V排g=1×103kg/m3×1.2×10﹣2m3×10N/kg=120N;
(2)W有=(G﹣F浮)×h=(360N﹣120N)×h=240N×h,
W总=Fs=100N×3h,
提起物体时滑轮组的机械效率:
η100%=80%。
(3)石块从刚露出水面到完全露出水面的过程中,石块排开水的体积减小,由阿基米德原理F浮=ρ水V排g可知受到的浮力减小;滑轮组受到的拉力增大,拉力做的有用功增大(相当于增大了提升的物重),额外功几乎不变,由此可知动滑轮的机械效率变大。
答:(1)石块浸没在水中时受到的浮力为120N;
(2)将石块提升到石块上表面与水面齐平的过程中滑轮组的机械效率为80%。
(3)若将石块从刚露出水面到完全露出水面的过程中也是匀速提升,石块所受浮力变小,滑轮组机械效率变大
一.选择题(共13小题)
1.如图所示,斜面高为1m,长为4m,用沿斜面向上大小为75N的拉力F,将重为200N的木箱由斜面底端匀速缓慢拉到顶端,下列关于做功的判断正确的是( )
A.木箱克服重力做功大小为300J
B.木箱受到的合力做功的大小为300J
C.木箱受到斜面的支持力做功大小为200J
D.木箱克服斜面摩擦力做功大小为100J
2.甲吊车比乙吊车的机械效率高,当它们分别把相同质量的物体匀速提升相同高度时,则( )
A.乙吊车做的总功较多
B.乙吊车做的有用功较多
C.甲吊车做的有用功较多
D.甲、乙两吊车做的总功相同
3.一滑轮组经改进提高了效率,把同一物体匀速升高同样的高度,改进后和改进前相比较( )
A.做的有用功减少了 B.做的有用功增加了
C.做的额外功增加了 D.做的总功减少了
4.下列关于机械效率的说法中正确的是( )
A.越省力的机械,机械效率越高
B.所做有用功越多的机械,机械效率越高
C.做功相等的情况下,额外功越少的机械,机械效率越高
D.做功越快的机械,机械效率越高
5.关于机械效率,下列说法正确的是( )
A.机械效率大的机器功率大
B.最优秀的机器的机械效率可达到100%
C.所做有用功越多,机械效率越高
D.有用功永远小于总功,所以机械效率小于1
6.如图所示,小明分别用甲、乙两个滑轮把同一袋沙子从地面提到二楼,用甲滑轮所做的总功为W1,机械效率为η1;用乙滑轮所做的总功为W2,机械效率为η2.若不计绳重与摩擦,则( )
A.W1=W2 η1=η2 B.W1=W2 η1<η2
C.W1<W2 η1>η2 D.W1>W2 η1<η2
7.如图所示斜面,斜面AB、AC的粗糙程度相同,把同一物体沿斜面BA和CA分别匀速拉到顶端A,若沿斜面的拉力F1=F2,斜面两边的机械效率分别为ηB、ηC,斜面两边的摩擦力分别为fB、fC,则下列判断正确的( )
A.ηB<ηC,fB<fC B.ηB>ηC,fB=fC
C.ηB<ηC,fB>fC D.ηB>ηC,fB<fC
8.如图甲,邻居大叔正吃力地把一重物搬上高台,放学回家的小明看见后急忙前去帮忙,他找来一块木板,搭成图乙所示的斜面,结果非常轻松的把同样的重物推到了高台上。关于这两种方法,下列说法正确的是( )
A.甲种情况下更省力 B.乙种情况的机械效率高
C.两人做同样多的有用功 D.小明做功的功率要大些
9.两台机械完成的有用功之比W1:W2=4:7,它们的机械效率分别为η1=60%,η2=75%,则两台机械所做总功之比为( )
A.5:7 B.7:5 C.16:35 D.35:16
10.用如图甲所示的装置来探究滑轮组的机械效率η与物重G物的关系,改变G物,竖直向上匀速拉动弹簧测力计,计算并绘出η与G物关系如图乙所示,若不计绳重和摩擦,则下列说法正确的是( )
A.同一滑轮组机械效率η随G物的增大而增大,最终将超过100%
B.G物不变,改变图甲中的绕绳方式,滑轮组机械效率将改变
C.此滑轮组动滑轮的重力为2N
D.当G物=6N时,机械效率η=66.7%
11.如图所示,小明探究滑轮组的机械效率,动滑轮重1N,用3N的拉力F通过该滑轮组匀速拉起重4N的物体,物体沿竖直方向上升0.2m.此过程中,额外功和机械效率分别是( )
A.0.2J 83.3% B.0.2J 80%
C.0.4J 80% D.0.4J 66.7%
12.如图所示,有一斜面长为L,高为h。现用力F沿斜面把重为G的物体从底端匀速拉到顶端,已知物体受到斜面的摩擦力为f,则下列关于斜面机械效率η的表达式正确的是( )
A. B.
C. D.
13.某同学用10牛的拉力,沿斜面将重为16牛的物体匀速拉上长4米、高2米的斜面顶端,则该斜面的机械效率及斜面对物体的摩擦力分别为( )
A.0.5,8牛 B.0.8,2牛 C.0.8,8牛 D.0.5,2牛
二.实验探究题(共4小题)
14.在探究“滑轮组机械效率”时,小明利用两组滑轮组进行了 4 次测量,用图甲所示装置测得前 3 组数据,用图乙装置测得第 4 组数据,如下表:
实验次数 物重 G 物/N 动滑轮重 G 动/N 钩码上升的高度 h/m 动力 F/N 动力作用点移动的距离 s/cm 滑轮组的机械效率 η
1 1 0.5 0.1 0.7 0.3 47.6%
2 2 0.5 0.1 1.1 0.3 60.6%
3 4 0.5 0.1 2 0.3
4 4 1 0.1 0.5 50.0%
(1)根据表中前 3 次实验数据,画出甲图中滑轮组的绕绳方法。
(2)在实验中,测量绳端拉力 F 时,应尽量 匀速拉动弹簧测力计,读出第 4 次实验时乙图中弹簧测力计的示数为 N,第 3 次实验时滑轮组的机械效率为 。
(3)由表中第 1、2、3 组数据可知: 。
(4)由表中第 3、4 组数据可知,滑轮组的机械效率与 有关。(摩擦力忽略不计)
15.如图所示是小芳同学探究斜面机械效率的实验装置图,实验前她做了如下猜想:
A.斜面的机械效率可能与斜面的粗糙程度有关
B.斜面的机械下列可能与斜面的倾斜程度有关
她在做实验时用弹簧测力计拉着同一物体沿斜面向上做匀速直线运动,分别进行了四次实验,并记录实验数据如下表所示:
实验次数 斜面倾斜程度 斜面粗糙 程度 木块重量G/N 斜面高h/m 拉力F/N 斜面长 s/m 有用功 W有/J 总功W总/J 机械效率 η
1 较缓 木板表面 2 0.1 0.6 0.5 0.2 0.3 67%
2 较陡 木板表面 2 0.2 1 0.5 0.4 0.5 80%
3 最陡 木板表面 2 0.3 1.4 0.5 0.6 0.7 86%
4 最陡 毛巾表面 2 0.3 1.6 0.5 0.6 0.8
(1)将表中所缺的数据补充完整。
(3)比较 两次实验可知猜想A是正确的。
(3)比较1、2、3次实验得到的结论是:当粗糙程度相同时,斜面越陡机械效率 。
(4)通过分析实验数据,还可以得出当斜面粗糙程度和高度都相同时,斜面越长越 (选填“省力”或“费力”)。
16.如图所示是小明测量杠杆机械效率的实验情景(杠杆的重力忽略不计)
(1)请在如表中把相关的数据填写完整
物体重 G/N 物体上升的 高度h/cm 弹簧测力计 的示数F/N 弹簧测力计移动 的竖直距离S/cm 有用功 W有/J 总功 W总/J 机械效率 η/%
4 30
(2)为提高本实验中杠杆的机械效率,请提一条合理的建议: 。
17.某小组在“测滑轮组机械效率的实验”中得到的数据如表所示,实验装置如图所示。
(1)实验中应沿竖直方向 缓慢拉动弹簧测力计。
(2)小组同学发现实验过程中边拉动边读数,弹簧测力计示数不稳定,应该静止读数。你认为他的想法 (选填“正确”或“不正确”),因为他没有考虑到 对滑轮组机械效率的影响。
实验次数 钩码重G/N 钩码上升高 度h/m 绳端拉力 F/N 绳端移动距离 s/m 机械 效率η
1 4 0.1 2.7 0.2 74%
2 4 0.1 1.8 0.3 74%
3 8 0.1 3.1 0.3 86%
4 8 0.1 2.5
(3)用丁图装置进行实验,得出表中第4次实验数据,请将表中的两个数据填写完整。
(4)通过比较 (填实验次数的序号)两次实验数据可得出结论:使用同一滑轮组提升同一重物时,滑轮组的机械效率与绳子段数无关。
(5)通过比较 (填实验次数的序号)两次实验数据可得出结论:同一滑轮组提升重物时,物重越大,滑轮组机械效率越高。
(6)通过比较3、4两次实验数据可得出结论: 。
三.计算题(共4小题)
18.小明利用如图所示的滑轮组提升重物,不计绳重和轮、轴间摩擦.当匀速提起重为480N的物体时,绳端的拉力F为200N。求:
(1)此过程中,滑轮组的机械效率为多大?
(2)动滑轮有多重?
(3)绳子能承受的最大拉力为400N,该滑轮组的最大机械效率为多大?
19.一辆质量是3.5t的汽车不慎陷入泥泞地面,汽车司机组织人们用如图所示的滑轮组将汽车拖出。已知整个过程中,水平拉力F是1000N,汽车沿水平方向匀速移动了1m,滑轮组的机械效率为90%.求:
(1)拉力F做的总功。
(2)有用功为多大。
(3)汽车受到的阻力大小。
20.小明在探究利用杠杆做功的实践活动中,把重G为285N的重物挂在杠杆的中点,用手竖直提起棒的一端,使物体缓慢匀速提升,如图所示。
(1)若不计杠杆自身重力和摩擦,求拉力F的大小?
(2)如杠杆是一根重为15N、质量均匀的硬棒,小明利用此杠杆2s内将重物提升了0.1m,则小明使用杠杆所做的有用功是多大?机械效率是多大?
21.如图所示,为了清洗水池,某工人重600N,站在池外地面上,用100N的拉力向下匀速拉动绳子提起一浸没在水中体积为1.2×10﹣2m3、重360N的石块(石块始终浸没在水中,且忽略水对石块的阻力,ρ水=1×103kg/m3,g=10N/kg)求:
(1)石块浸没在水中时受到的浮力;
(2)将石块提升到石块上表面与水面齐平的过程中滑轮组的机械效率。
(3)若将石块从刚露出水面到完全露出水面的过程中也是匀速提升,试分析在此过程中,石块所受浮力和滑轮组机械效率的变化情况。
参考答案
一.选择题(共13小题)
1.【解析】解:A、由题意知,木箱的重力G=200N,h=1m,
则克服重力做功:W有用=Gh=200N×1m=200J,故A错误;
B、木箱沿斜面匀速缓慢运动,处于平衡状态,则木箱所受合力为零,所以合力做功大小为0J,故B错误;
C、木箱移动方向与支持力方向垂直,所以斜面的支持力做功为0J,故C错误;
D、拉力F做的功:W总=FL=75N×4m=300J;
则克服摩擦力做功:W额=W总﹣W有用=300J﹣200J=100J,故D正确。
【答案】D。
2.【解析】解:
BC、根据公式W有用=Gh=mgh可知甲、乙吊车做的有用功相同,BC选项错误;
AD、两辆吊车做的有用功相同,乙的效率较低,所以乙吊车做总功较多,A选项正确,D选项错误。
【答案】A。
3.【解析】解:把同一物体匀速提升同样的高度,
由W=Gh可知:利用滑轮组做的有用功相同;
滑轮组改进后提高机械效率,
由η100%可知:改装后滑轮组的机械效率提高了,所以做的总功减少;
由W总=W有+W额知:改装后利用滑轮组做的额外功减少;
由上述分析得出,A、B、C错,D正确。
【答案】D。
4.【解析】解:
A、机械效率是指有用功占总功的百分比,与是否省力没有必然的联系,故A说法错误;
B、效率指有用功占总功的比值,有用功多,如果额外功更多,则效率不一定高,故B说法错误;
C、做功相等的情况下,额外功越少的机械,有用功占的越多,所以机械效率越高,故C说法正确;
D、机械做功越快,表示功率越大,机械效率与功率间没有必然联系,故D说法错误。
【答案】C。
5.【解析】解:
A、有用功与总功的比值叫机械效率,而功率是功与时间的比值,二者没有必然的联系,故A错误;
B、使用机械时,不可避免地要做额外功,所以总功一定大于有用功,即机械效率不可能达到100%,故B错误;
C、有用功与总功的比值叫机械效率,只知道有用功多,机械效率不一定高,故C错误;
D、使用机械时,不可避免地要做额外功,有用功永远小于总功,所以机械效率一定小于1,故D正确。
【答案】D。
6.【解析】解:
(1)因为小明分别用甲、乙两滑轮把同一袋沙从地面提到二楼,所以两种情况的有用功相同;
(2)当有用功一定时,乙中所做的总功为对一袋沙所做的功,利用机械时做的额外功越少,则总功就越少,机械效率就越高;
又因为甲是动滑轮,甲中所做的总功还要加上对动滑轮所做的功,利用甲滑轮做的额外功多,则总功越多,机械效率越低。即W1>W2,η1<η2。
【答案】D。
7.【解析】解:(1)由题知,同一物体提升的高度h相同,由W有=Gh可知,有用功相同,
因AB<AC,且拉力相同,
所以,由W总=Fs可知,F2做的总功多,
由η100%可知,右边斜面的机械效率低,即ηB>ηC,故AC错误;
(2)影响滑动摩擦力大小的因素有两个:压力大小和接触面的粗糙程度,
物体分别沿斜面BA和CA运动,接触面的粗糙程度相同,斜面越陡,则压力越小,滑动摩擦力越小,由图知BA斜面更陡一些,所以fB<fC,故B错误、D正确。
【答案】D。
8.【解析】解:
A、斜面是一种省力机械,利用斜面将物体推上高台可更省力,所以,甲种情况费力,故A错误;
B、由于乙中情况需要克服摩擦做功,所以乙种情况下的机械效率小。故B错误;
C、这两种方法,都把重物推到了高台上,两人做同样多的有用功,克服重力做功相同,故C正确;
D、功率等于功与时间的比值,由于题中没有给出时间,不能确定哪个做功的功率大。故D错误。
【答案】C。
9.【解析】解:由η1=60%,η2=75%可知:η1:η2=4:5.而η,所以W总。
有用功W1:W2=4:7,则总功W1总:W2总:5:7,故选A。
10.【解析】解:A、使用滑轮组时,克服物重的同时,不可避免地要克服动滑轮重、摩擦和绳子重做额外功,所以总功一定大于有用功;由公式η知:机械效率一定小于1,即同一滑轮组机械效率η随G物的增大而增大,但最终不能超过100%,故A错误;
B、G物不变,改变图甲中的绕绳方式,如图所示,
因为此图与题干中甲图将同一物体匀速提高相同的高度,所以所做的有用功相同,
忽略绳重及摩擦时,额外功:W额=G轮h,即额外功W额相同,
又因为W总=W有+W额,所以总功相同,
由η可知,两装置的机械效率相同,即η1=η2.故B错误;
C、由图可知,G=12N,此时η=80%,
则η,即80%,
解得G动=3N,故C错误;
D、G物=6N时,机械效率η100%100%100%100%≈66.7%.故D正确。
【答案】D。
11.【解析】解:
有用功为W有用=Gh=4N×0.2m=0.8J;
绳子拉下的长度为s=2h=2×0.2m=0.4m,
拉力做的总功为W总=Fs=3N×0.4m=1.2J。
额外功为W额=W总﹣W有用=1.2J﹣0.8J=0.4J;
机械效率为η100%≈66.7%。
【答案】D。
12.【解析】解:
斜面的高为h,物体的重力为G,
则有用功为:W有用=Gh,
又因为斜面长为L,拉力为F,
所以拉力所做的总功为:W总=FL,
则斜面的机械效率为:η100%100%;
而物体受到斜面的摩擦力为f,
则克服摩擦力做的额外功为:W额外=fL,
所以总功为:W总=W有用+W额外=Gh+fL,
则斜面的机械效率为:η100%100%,故ABC错误,D正确。
【答案】D。
13.【解析】解:W有用=Gh=16N×2m=32J,
W总=Fs=10N×4m=40J,
η80%=0.8;
∵W总=W有用+W额,
∴W额=W总﹣W有用=40J﹣32J=8J,
∵W额=fs,
∴f2N。
【答案】B。
二.实验探究题(共4小题)
14.【解析】解:
(1)表中前 3 次实验数据,根据s=nh可得,绳子的有效段数:n3;
根据偶定奇动原则,绳子应系在动滑轮的上面挂钩上,由此绕线,如下所示:
(2)在实验中,测量绳端拉力F 时,应尽量竖直向上匀速拉动弹簧测力计,此时系统处于平衡状态,测力计示数才等于拉力的大小;
图乙中测力计分度值为0.2N,乙图中弹簧测力计的示数为 1.6N,
第 3 次实验时滑轮组的机械效率为:
η100%100%≈66.7%。
(3)图甲所示装置测得前 3 组数据,由表中第 1、2、3 组数据可知:使用同一滑轮组,提升的物体越重,机械效率越大;
(4)由题知,小明利用两组滑轮组进行了 4 次测量,用图甲所示装置测得前 3 组数据,则用图乙所示装置测得第4组数据;
由表中第 3、4 组数据可知,提升物体的重力相同,第3次实验要克服1个动滑轮重(0.5N)做额外功,而第4次实验要克服2个动滑轮重(1N)做额外功,两次的机械效率不同,说明滑轮组的机械效率与动滑轮重有关。
【答案】(1)如上所示;(2)竖直向上;1.6;66.7%;(3)同一滑轮组,提升的物重越大,机械效率越大;(4)动滑轮重。
15.【解析】解:
(1)由表中数据,机械效率η100%=75%;
(2)要验证斜面的机械效率可能与斜面的粗糙程度有关,要控制斜面倾斜程度相同,只改变斜面的粗糙程度,故由表中3、4两次实验数据可知,在斜面粗糙程度不同而斜面的倾斜程度相同时,斜面的效率不同,由此可知,斜面的机械效率与斜面的粗糙程度有关,故猜想A正确;
(3)由表中第1、2、3此实验数据可知,当斜面粗糙程度相同时,斜面越陡,机械效率越高;
(4)分析表中数据可知,斜面的长度相同,都是0.5m,高度越高,拉力F越大,即:斜面越陡越费力,越缓越省力。
由此可推知,当斜面的高度相同时,斜面越长,则倾斜程度越缓,此时会越省力。
【答案】(1)75%;(2)3、4;(3)越高;(4)省力。
16.【解析】解:(1)从实验的物体的重力标识为4N,测力计指针对应的刻度是2.4N即拉力的大小;
物体升高的高度以物体上边沿为参照点,位置高度变化为由35cm到50cm,共移动15cm;
测力计竖直移动的距离以杠杆右端为参照点,位置高度变化为由43cm到13cm,共移动30cm;
并将读数记录在表格中,则:
W有=Gh=4N×0.15m=0.6J;
W总=FS=2.4N×0.3m=0.72J;
所以η100%100%≈83.3%。
(2)提高机械效率的方法根本途径是:减小机械的重力和机械之间的摩擦。使用杠杆时,杠杆只是转动,杠杆的重力产生的额外功很少,主要是杠杆的摩擦,所以选择支点灵活的杠杆或在支点所在轴处加润滑油等减小摩擦的方法都可以提高机械效率。
【答案】(1)15;2.4;0.6;0.72;83.3;(2)选择支点灵活的杠杆或在支点所在轴处加润滑油。
17.【解析】解:
(1)在测量滑轮组机械效率的实验中,应竖直向上缓慢匀速拉动弹簧测力计,这样保证滑轮组处于平衡状态,且便于读出测力计的示数;
(2)若在静止时读数,测力计没有测出绳子与滑轮间的摩擦,测得的拉力偏小,他的想法不正确;原因是没有考虑到摩擦对滑轮组机械效率的影响。
(3)用丁图进行实验,可以看出绳子段数为4段,则绳端移动距离:
s=nh=4×0.1m=0.4m,
滑轮组的机械效率:
η100%=80%;
如下表所示:
实验次数 钩码重G/N 钩码上升高 度h/m 绳端拉力 F/N 绳端移动距离 s/m 机械 效率η
1 4 0.1 2.7 0.2 74%
2 4 0.1 1.8 0.3 74%
3 8 0.1 3.1 0.3 86%
4 8 0.1 2.5 0.4 80%
(4)在比较滑轮组的机械效率与绳子段数的关系时,应保持滑轮组相同、物重相同,而绳子绕法不同,因此比较1和2两次实验即可得出结论;
(5)研究同一滑轮组提升重物时,滑轮组机械效率与提升物体的重力的关系时,要控制其它因素相同,只改变提升物体的重力,故通过比较2、3可得出滑轮组机械效率与物重的关系;
(6)通过比较3、4两次实验数据知,提升物体的重力相同,而丙中动滑轮的重力小于丁中动滑轮的重力和,丙的机械效率较大,故可得出的结论:不同滑轮组提升相同重物时,动滑轮越轻,滑轮组机械效率越高(不同滑轮组提升相同重物时,动滑轮越重,滑轮组机械效率越低)。
【答案】
(1)匀速;(2)不正确;摩擦;(3)如上表所示;(4)1、2;(5)2、3;(6)不同滑轮组提升相同重物时,动滑轮越轻,滑轮组机械效率越高(不同滑轮组提升相同重物时,动滑轮越重,滑轮组机械效率越低)。
三.计算题(共4小题)
18.【解析】解:(1)由图可知,滑轮组绳子的有效股数n=3,则滑轮组的机械效率:
η100%100%100%100%100%=80%;
(2)不计绳重和轮、轴间摩擦,由F(G+G动)可得,动滑轮的重力:
G动=nF﹣G=3×200N﹣480N=120N;
(3)绳子能承受的最大拉力为400N,则提升物体的最大重力:
G大=nF大﹣G动=3×400N﹣120N=1080N,
该滑轮组的最大机械效率:
η大100%100%100%100%100%=90%。
答:(1)此过程中,滑轮组的机械效率为80%;
(2)动滑轮的重力为120N;
(3)绳子能承受的最大拉力为400N,该滑轮组的最大机械效率为90%。
19.【解析】解:
(1)由图知,n=3,
拉力端移动的距离:s=3s物=3×1m=3m,
拉力F做的总功:W总=Fs=1000N×3m=3×103J;
(2)由η可得有用功:
W有用=W总η=3×103J×90%=2.7×103J。
(3)因为W有用=fs物,
则汽车受到的阻力:
f2.7×103N。
答:(1)拉力F做的总功为3×103J;
(2)有用功为2.7×103J;
(3)汽车受到的阻力大小为2.7×103N。
20.【解析】解:(1)由于重物挂在杠杆的中点,用手竖直提起棒的一端,则L1=2L2,若不计杠杆自身重力和摩擦,由杠杆原理FL1=GL2可得:
F142.5N。
(2)所做的有用功为:W有用=Gh=285N×0.1m=28.5J,
所做的额外功为:W额外=G杆h=15N×0.1m=1.5J,
总功为:W总=W有用+W额外=28.5J+1.5J=30J,
机械效率为:η100%100%=95%。
答:(1)若不计杠杆自身重力和摩擦,拉力F是142.5N。
(2)小明使用杠杆所做的有用功为28.5J.机械效率是95%。
21.【解析】解:
(1)石块浸没在水中,V排=V=1.2×10﹣2m3,
所受浮力:
F浮=ρ水V排g=1×103kg/m3×1.2×10﹣2m3×10N/kg=120N;
(2)W有=(G﹣F浮)×h=(360N﹣120N)×h=240N×h,
W总=Fs=100N×3h,
提起物体时滑轮组的机械效率:
η100%=80%。
(3)石块从刚露出水面到完全露出水面的过程中,石块排开水的体积减小,由阿基米德原理F浮=ρ水V排g可知受到的浮力减小;滑轮组受到的拉力增大,拉力做的有用功增大(相当于增大了提升的物重),额外功几乎不变,由此可知动滑轮的机械效率变大。
答:(1)石块浸没在水中时受到的浮力为120N;
(2)将石块提升到石块上表面与水面齐平的过程中滑轮组的机械效率为80%。
(3)若将石块从刚露出水面到完全露出水面的过程中也是匀速提升,石块所受浮力变小,滑轮组机械效率变大
