7.3.2 多边形内角和
文档属性
| 名称 | 7.3.2 多边形内角和 |

|
|
| 格式 | zip | ||
| 文件大小 | 677.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-26 00:00:00 | ||
图片预览





文档简介
课件17张PPT。 多边形的内角和问题2:你知道长方形和正方形的内角和是多少?
其它四边形的内角和是多少?
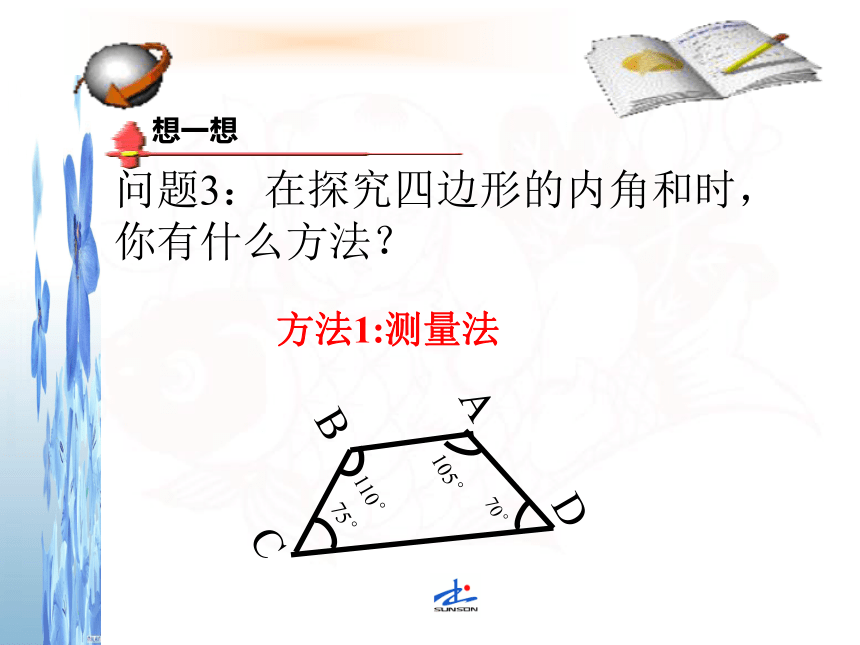
问题1:你还记得三角形内角和是多少度?(三角形内角和 180°)(都是360°)想一想问题3:在探究四边形的内角和时,你有什么方法?想一想方法1:测量法想一想方法2:分割法画四边形的对角线把它分成两个三角形,根据三角形内角和为180,所以四边形的内角和是2×180°=360°对角线把五边形分成了三个三角形,根据三角形内角和为180,所以五边形的内角和是那么五边形、六边形的内角和是多少呢?对角线把六边形分成了四个三角形,根据三角形内角和为180°,所以六边形的内角和是
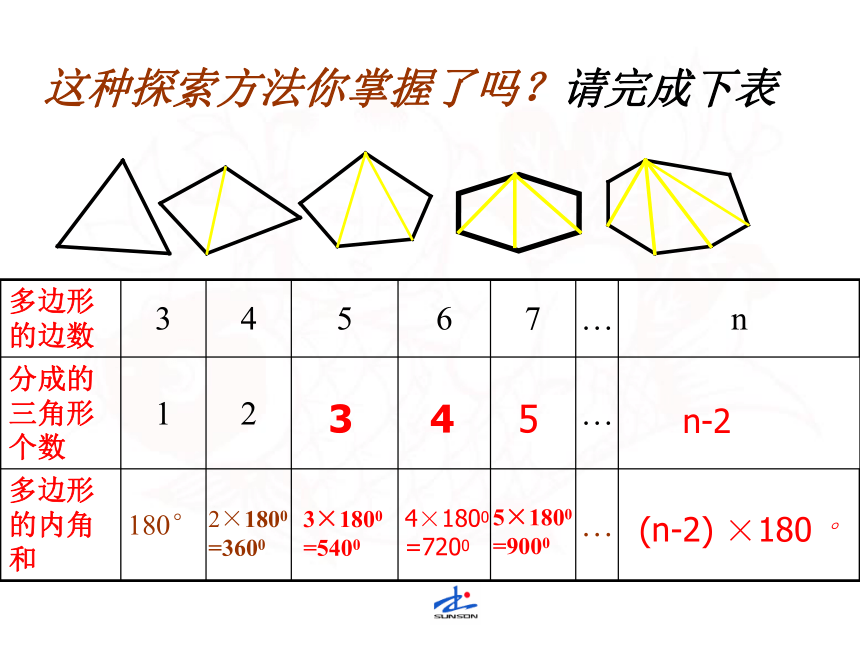
3×180°=540°4×180°=720°这种探索方法你掌握了吗?请完成下表345n-22×1800
=36003×1800
=54004×1800
=7200 5×1800
=9000(n-2) ×180 ° n边形内角和等于
议一议(n-2)× 180°
2、我们也可以利用下列不同的方法分割多边形,得到n边形的内角和公式
试一试1、(抢答) 8边形的内角和等于多少度? 十边形呢?(8-2) × 180°=(10-2) ×180°=1440°1080°2.求下列图形中x的值:做一做例1,如图AD ⊥AB,BC ⊥CD, 那么∠B与∠D的关系是因为AD ⊥AB,BC ⊥CD,所以∠A= ∠C= 90° 因为四边形内角和等于360°
所以∠B+∠D= 180° 如果一个四边形的一组对角
互补,那么另一组对角也互补。∠B与∠D是互补。解:例2、在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和。六边形的外角和等于多少?
6×180°-(6-2)×180
=2×180°
=360°探究如果将例2中六边形换为 n边形
(n的值是不小于3的任意整数),
可以得到同样结果吗?N边形的外角和= n×180°-(n-2)×180°=2×180°=360°结论由上面的探究可以得到:多边形的外角和等于360°课后思考1、小明在计算某个多边形的内角和时,由于粗心他漏掉一个内角,求得的内角和1680° ,你能否求得正确结果呢?
2、一天小明爸爸给小明出了一道智力题考考他。将一个多边形截去一个角后(没有过顶点)得到多边形的内角和将会( )
A、不变 B、增加 180°
C、减少 180° D、无法确定1、我们学会了许多解决数学问题的思想方法,如将多边形问题转化为三角形问题,以及类比方法,化未知为已知的思想方法等。
2、通过探索多边形的内角和公式,我们尝试了从不同的角度寻求解决问题的方法,并且能有效地解决问题。
3、我们还学会了运用多边形内角和公式进行相关计算。本节课收获布置作业:习题7.3 5 、7 、 8
其它四边形的内角和是多少?
问题1:你还记得三角形内角和是多少度?(三角形内角和 180°)(都是360°)想一想问题3:在探究四边形的内角和时,你有什么方法?想一想方法1:测量法想一想方法2:分割法画四边形的对角线把它分成两个三角形,根据三角形内角和为180,所以四边形的内角和是2×180°=360°对角线把五边形分成了三个三角形,根据三角形内角和为180,所以五边形的内角和是那么五边形、六边形的内角和是多少呢?对角线把六边形分成了四个三角形,根据三角形内角和为180°,所以六边形的内角和是
3×180°=540°4×180°=720°这种探索方法你掌握了吗?请完成下表345n-22×1800
=36003×1800
=54004×1800
=7200 5×1800
=9000(n-2) ×180 ° n边形内角和等于
议一议(n-2)× 180°
2、我们也可以利用下列不同的方法分割多边形,得到n边形的内角和公式
试一试1、(抢答) 8边形的内角和等于多少度? 十边形呢?(8-2) × 180°=(10-2) ×180°=1440°1080°2.求下列图形中x的值:做一做例1,如图AD ⊥AB,BC ⊥CD, 那么∠B与∠D的关系是因为AD ⊥AB,BC ⊥CD,所以∠A= ∠C= 90° 因为四边形内角和等于360°
所以∠B+∠D= 180° 如果一个四边形的一组对角
互补,那么另一组对角也互补。∠B与∠D是互补。解:例2、在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和。六边形的外角和等于多少?
6×180°-(6-2)×180
=2×180°
=360°探究如果将例2中六边形换为 n边形
(n的值是不小于3的任意整数),
可以得到同样结果吗?N边形的外角和= n×180°-(n-2)×180°=2×180°=360°结论由上面的探究可以得到:多边形的外角和等于360°课后思考1、小明在计算某个多边形的内角和时,由于粗心他漏掉一个内角,求得的内角和1680° ,你能否求得正确结果呢?
2、一天小明爸爸给小明出了一道智力题考考他。将一个多边形截去一个角后(没有过顶点)得到多边形的内角和将会( )
A、不变 B、增加 180°
C、减少 180° D、无法确定1、我们学会了许多解决数学问题的思想方法,如将多边形问题转化为三角形问题,以及类比方法,化未知为已知的思想方法等。
2、通过探索多边形的内角和公式,我们尝试了从不同的角度寻求解决问题的方法,并且能有效地解决问题。
3、我们还学会了运用多边形内角和公式进行相关计算。本节课收获布置作业:习题7.3 5 、7 、 8
