九年级下册数学第三章圆单元测试五(附答案)
文档属性
| 名称 | 九年级下册数学第三章圆单元测试五(附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 360.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-26 00:00:00 | ||
图片预览


文档简介
九年级下册数学第三章圆单元测试五(附答案)
学校:___________姓名:___________班级:___________考号:___________
题号
一
二
三
四
总分
得分
第I卷(选择题)
评卷人
得分
一、选择题
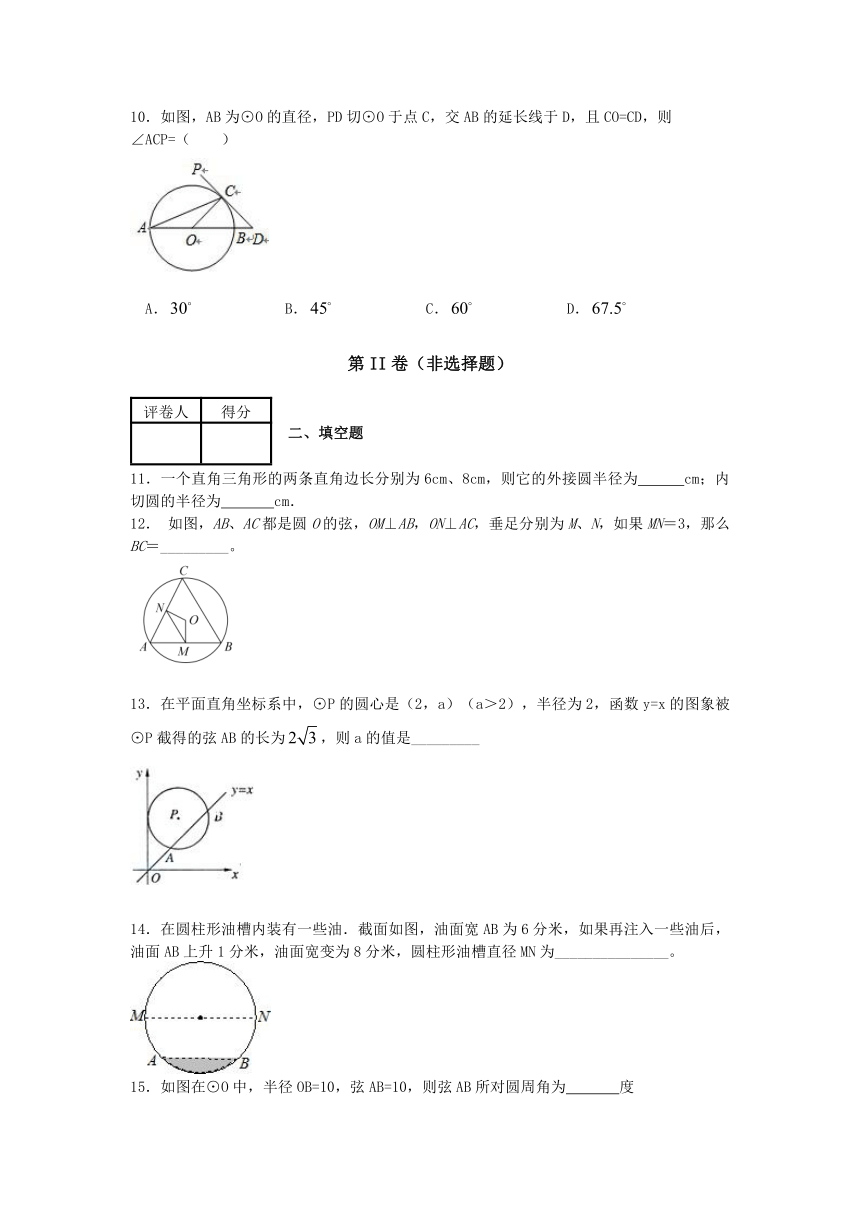
1. 如图,AB为⊙O的直径,点C在⊙O上,若∠C=,则∠BOC的度数是( )
A. B.
C. D.
2.⊙半径为3cm,到直线L的距离为2cm,则直线L与⊙位置关系为( )
A、相交 B、相切 C、相离 D、不能确定
3.一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2
米,则此输水管道的直径是
A.0.5 B.1 C.2 D.4
4.如图是正方体盒子的表面展开图,则下列说法中错误的是( )
A.当折叠成正方体纸盒时,点F与点E,C重合
B.过点A、B、C、D、E、F、G七个点中的n个点作圆,则n的最大值为4
C.以点A、B、C、D、E、F、G中的四个点为顶点的四边形中平行四边形有2个
D.设图中每个小正方形的边长为1,则能覆盖这个图形的最小的圆的直径为
5.如图,扇形DOE的半径为3,边长为的菱形OABC的顶点A,C,B分别在OD,OE,上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )
A. B. C. D.
6.已知一个圆锥的底面半径为3cm,母线长为10cm,则这个圆锥的侧面积为( )
A. 15πcm2 B. 30πcm2 C. 60πcm2 D. 3cm2
7.如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )
A.1 B. C. D.
8.已知⊙的半径为5,⊙的半径为3,两圆的圆心距为7,则两圆的位置关系是
外离 外切 内切 相交
9.已知⊙O1、⊙O2的半径分别为3cm、5cm,且它们的圆心距为8cm,则⊙O1与⊙O2的位置关系是( )
A.外切 B.相交 C.内切 D.内含
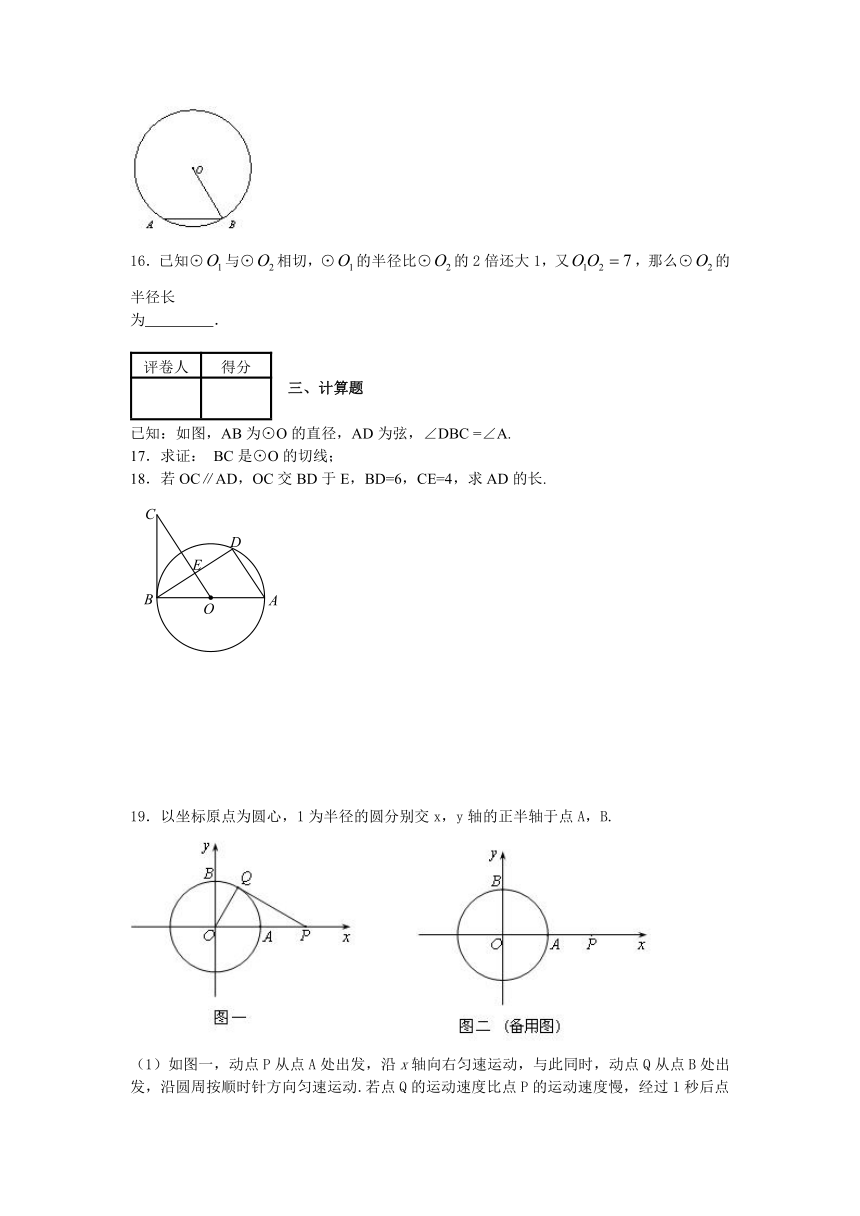
10.如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则
∠ACP=( )
A. B. C. D.
第II卷(非选择题)
评卷人
得分
二、填空题
11.一个直角三角形的两条直角边长分别为6cm、8cm,则它的外接圆半径为 cm;内切圆的半径为 cm.
12. 如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=3,那么BC=_________。
13.在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是_________
14.在圆柱形油槽内装有一些油.截面如图,油面宽AB为6分米,如果再注入一些油后,油面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为_______________。
15.如图在⊙O中,半径OB=10,弦AB=10,则弦AB所对圆周角为 度
16.已知⊙与⊙相切,⊙的半径比⊙的2倍还大1,又,那么⊙的半径长
为 .
评卷人
得分
三、计算题
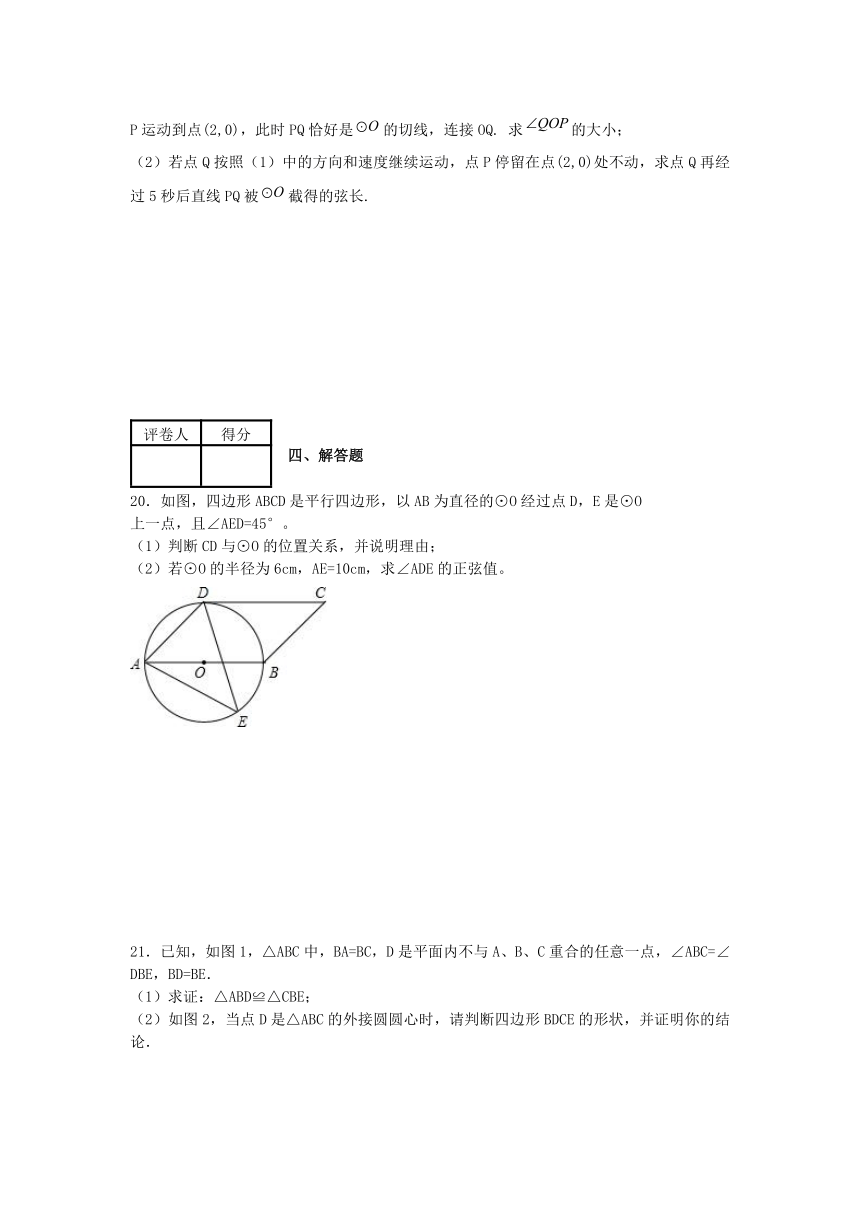
已知:如图,AB为⊙O的直径,AD为弦,∠DBC =∠A.
17.求证: BC是⊙O的切线;
18.若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
19.以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.
(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是的切线,连接OQ. 求的大小;
(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被截得的弦长.
评卷人
得分
四、解答题
20.如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O
上一点,且∠AED=45°。
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为6cm,AE=10cm,求∠ADE的正弦值。
21.已知,如图1,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,∠ABC=∠DBE,BD=BE.
(1)求证:△ABD≌△CBE;
(2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BDCE的形状,并证明你的结论.
22.在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.
(Ⅰ)探究新知:
如图① ⊙O是△ABC的内切圆,与三边分别相切于点E、F、G..
(1)求证内切圆的半径r1=1;
(2)求tan∠OAG的值;
(Ⅱ)结论应用
(1)如图②若半径为r2的两个等圆⊙O1、⊙O2外切,且⊙O1与AC、AB相切,⊙O2与BC、AB相切,求r2的值;
(2)如图③若半径为rn的n个等圆⊙O1、⊙O2、…、⊙On依次外切,且⊙O1与AC、AB相切,⊙On与BC、AB相切,⊙O1、⊙O2、…、⊙On均与AB相切,求rn的值.
23.如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为的中点.
(1)求证:OF∥BD;
(2)若,且⊙O的半径R=6cm.①求证:点F为线段OC的中点; ②求图中阴影部分(弓形)的面积.
24.如图1,在第一象限内,直线与过点且平行于轴的直线相交于点,半径为的⊙与直线、轴分别相切于点、,且与直线分别交于不同的、两点.
(1)当点A的坐标为时,
① 填空:= , = ,= ;
②如图2,连结,交直线于,当时,试说明以、 、 、为顶点的四边形是等腰梯形;
(2)在图1中,连结并延长交⊙于点,试探索:对不同的取值,经过、、三点的抛物线,的值会变化吗?若不变,求出的值;若变化,请说明理由.
25.已知:如图,AB是⊙O的直径,点C在⊙O上,△ABC的外角平分线BD交⊙O于D,DE
与⊙O相切,交CB的延长线于E.
⑴ 判断直线AC和DE是否平行,并说明理由;
⑵ 若∠A=30°,BE=1cm,分别求线段DE和 的长。(直接写出最后结果).
参考答案
1.C
2.A
3.B
4.D
5.D
6.B
7.C。
8.D
9.A。
10.D
11.5;2
12.6
13.
14.10分米
15.30°或150°
16.2或6
17.证明:(1)∵AB为⊙O的直径
∴(D=90°, (A+(ABD=90°
∵∠DBC =∠A
∴∠DBC+∠ABD=90°
∴BC⊥AB
∴BC是⊙O的切线
18.∵OC∥AD,(D=90°,BD=6
∴OC⊥BD
∴BE=BD=3
∵O是AB的中点
∴AD=2EO -
∵BC⊥AB ,OC⊥BD
∴△CEB∽△BEO,∴
∵CE=4, ∴
∴AD=
19.(1)60°(2)
20.(1)CD与⊙O相切,理由见解析(2)
21.(1)略(2)四边形BDEF是菱形,证明略
22.(Ⅰ)探究新知(1)略(2)1/2(Ⅱ)结论应用(1)(2)
23.(1)略(2)①略②cm2
24.(1)① ,, ;
② 连结、、、、MQ(如图1),
切⊙于, ∥轴
∴,且
又∵
∴四边形是平行四边形
∴∥
在中,,∴
依题意,在四边形中,,
∴ ∴
∴、、在同一直线(直径)上
∴∥ 且,又 ∴
又,为等边三角形,∴
∴
∴四边形是等腰梯形
注:也可证明.
(2)的值不变. 理由如下:
如图,与交于点,连结、,
∵是⊙直径 ∴
又∵ ∴
∴ ∴
即 ………………(Ⅰ)
(注:本式也可由∽得到)
∵在平移中,图形的形状及特征保持不变,
抛物线的图象可通过的图象平移得到.
∴可以将问题转化为:点在轴上,点、在轴上进行探索(如图4)
由图形的对称性得点为抛物线顶点,依题意设,则经过、、三点的抛物线为:,由,及(Ⅰ)式得:,
∴ ∴, 解得.
故的值不变 .
25..⑴ 平行 ;
理由是:
联结OD,∵DE与⊙O相切,
∴ OD⊥DE.
∵ OB=OD, ∴∠ODB=∠OBD.
∵ BD是∠ABE的平分线,
即∠ABD=∠DBE,
∴ ∠ODB=∠DBE.
∴ OD∥BE.
∴ BE⊥DE,即DE⊥CE.
∵ AB是⊙O的直径,点C在⊙O上,∴AC⊥CE
∴ AC∥DE.
⑵ ,.
26.连接AO并延长交扇形、圆于点E、F
∵BC是⊙O的直径,∴∠BAC=90°
∵ ∴AB=AC,
∵AO=BO ∴AF⊥BC
(1)当⊙O的半径为2时:AC=AB=2
∴S阴影=;
(2)当⊙O的半径为R(R>0)时:AC=AB=R
阴影部分扇形的弧长为:πR
EF=2R-R,以EF为直径作圆,是剩余材料中所作的最大的圆,其圆周长为:(2-)πR
∵πR>(2-)πR
∴不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.
学校:___________姓名:___________班级:___________考号:___________
题号
一
二
三
四
总分
得分
第I卷(选择题)
评卷人
得分
一、选择题
1. 如图,AB为⊙O的直径,点C在⊙O上,若∠C=,则∠BOC的度数是( )
A. B.
C. D.
2.⊙半径为3cm,到直线L的距离为2cm,则直线L与⊙位置关系为( )
A、相交 B、相切 C、相离 D、不能确定
3.一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2
米,则此输水管道的直径是
A.0.5 B.1 C.2 D.4
4.如图是正方体盒子的表面展开图,则下列说法中错误的是( )
A.当折叠成正方体纸盒时,点F与点E,C重合
B.过点A、B、C、D、E、F、G七个点中的n个点作圆,则n的最大值为4
C.以点A、B、C、D、E、F、G中的四个点为顶点的四边形中平行四边形有2个
D.设图中每个小正方形的边长为1,则能覆盖这个图形的最小的圆的直径为
5.如图,扇形DOE的半径为3,边长为的菱形OABC的顶点A,C,B分别在OD,OE,上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )
A. B. C. D.
6.已知一个圆锥的底面半径为3cm,母线长为10cm,则这个圆锥的侧面积为( )
A. 15πcm2 B. 30πcm2 C. 60πcm2 D. 3cm2
7.如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )
A.1 B. C. D.
8.已知⊙的半径为5,⊙的半径为3,两圆的圆心距为7,则两圆的位置关系是
外离 外切 内切 相交
9.已知⊙O1、⊙O2的半径分别为3cm、5cm,且它们的圆心距为8cm,则⊙O1与⊙O2的位置关系是( )
A.外切 B.相交 C.内切 D.内含
10.如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则
∠ACP=( )
A. B. C. D.
第II卷(非选择题)
评卷人
得分
二、填空题
11.一个直角三角形的两条直角边长分别为6cm、8cm,则它的外接圆半径为 cm;内切圆的半径为 cm.
12. 如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=3,那么BC=_________。
13.在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是_________
14.在圆柱形油槽内装有一些油.截面如图,油面宽AB为6分米,如果再注入一些油后,油面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为_______________。
15.如图在⊙O中,半径OB=10,弦AB=10,则弦AB所对圆周角为 度
16.已知⊙与⊙相切,⊙的半径比⊙的2倍还大1,又,那么⊙的半径长
为 .
评卷人
得分
三、计算题
已知:如图,AB为⊙O的直径,AD为弦,∠DBC =∠A.
17.求证: BC是⊙O的切线;
18.若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
19.以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.
(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是的切线,连接OQ. 求的大小;
(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被截得的弦长.
评卷人
得分
四、解答题
20.如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O
上一点,且∠AED=45°。
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为6cm,AE=10cm,求∠ADE的正弦值。
21.已知,如图1,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,∠ABC=∠DBE,BD=BE.
(1)求证:△ABD≌△CBE;
(2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BDCE的形状,并证明你的结论.
22.在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.
(Ⅰ)探究新知:
如图① ⊙O是△ABC的内切圆,与三边分别相切于点E、F、G..
(1)求证内切圆的半径r1=1;
(2)求tan∠OAG的值;
(Ⅱ)结论应用
(1)如图②若半径为r2的两个等圆⊙O1、⊙O2外切,且⊙O1与AC、AB相切,⊙O2与BC、AB相切,求r2的值;
(2)如图③若半径为rn的n个等圆⊙O1、⊙O2、…、⊙On依次外切,且⊙O1与AC、AB相切,⊙On与BC、AB相切,⊙O1、⊙O2、…、⊙On均与AB相切,求rn的值.
23.如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为的中点.
(1)求证:OF∥BD;
(2)若,且⊙O的半径R=6cm.①求证:点F为线段OC的中点; ②求图中阴影部分(弓形)的面积.
24.如图1,在第一象限内,直线与过点且平行于轴的直线相交于点,半径为的⊙与直线、轴分别相切于点、,且与直线分别交于不同的、两点.
(1)当点A的坐标为时,
① 填空:= , = ,= ;
②如图2,连结,交直线于,当时,试说明以、 、 、为顶点的四边形是等腰梯形;
(2)在图1中,连结并延长交⊙于点,试探索:对不同的取值,经过、、三点的抛物线,的值会变化吗?若不变,求出的值;若变化,请说明理由.
25.已知:如图,AB是⊙O的直径,点C在⊙O上,△ABC的外角平分线BD交⊙O于D,DE
与⊙O相切,交CB的延长线于E.
⑴ 判断直线AC和DE是否平行,并说明理由;
⑵ 若∠A=30°,BE=1cm,分别求线段DE和 的长。(直接写出最后结果).
参考答案
1.C
2.A
3.B
4.D
5.D
6.B
7.C。
8.D
9.A。
10.D
11.5;2
12.6
13.
14.10分米
15.30°或150°
16.2或6
17.证明:(1)∵AB为⊙O的直径
∴(D=90°, (A+(ABD=90°
∵∠DBC =∠A
∴∠DBC+∠ABD=90°
∴BC⊥AB
∴BC是⊙O的切线
18.∵OC∥AD,(D=90°,BD=6
∴OC⊥BD
∴BE=BD=3
∵O是AB的中点
∴AD=2EO -
∵BC⊥AB ,OC⊥BD
∴△CEB∽△BEO,∴
∵CE=4, ∴
∴AD=
19.(1)60°(2)
20.(1)CD与⊙O相切,理由见解析(2)
21.(1)略(2)四边形BDEF是菱形,证明略
22.(Ⅰ)探究新知(1)略(2)1/2(Ⅱ)结论应用(1)(2)
23.(1)略(2)①略②cm2
24.(1)① ,, ;
② 连结、、、、MQ(如图1),
切⊙于, ∥轴
∴,且
又∵
∴四边形是平行四边形
∴∥
在中,,∴
依题意,在四边形中,,
∴ ∴
∴、、在同一直线(直径)上
∴∥ 且,又 ∴
又,为等边三角形,∴
∴
∴四边形是等腰梯形
注:也可证明.
(2)的值不变. 理由如下:
如图,与交于点,连结、,
∵是⊙直径 ∴
又∵ ∴
∴ ∴
即 ………………(Ⅰ)
(注:本式也可由∽得到)
∵在平移中,图形的形状及特征保持不变,
抛物线的图象可通过的图象平移得到.
∴可以将问题转化为:点在轴上,点、在轴上进行探索(如图4)
由图形的对称性得点为抛物线顶点,依题意设,则经过、、三点的抛物线为:,由,及(Ⅰ)式得:,
∴ ∴, 解得.
故的值不变 .
25..⑴ 平行 ;
理由是:
联结OD,∵DE与⊙O相切,
∴ OD⊥DE.
∵ OB=OD, ∴∠ODB=∠OBD.
∵ BD是∠ABE的平分线,
即∠ABD=∠DBE,
∴ ∠ODB=∠DBE.
∴ OD∥BE.
∴ BE⊥DE,即DE⊥CE.
∵ AB是⊙O的直径,点C在⊙O上,∴AC⊥CE
∴ AC∥DE.
⑵ ,.
26.连接AO并延长交扇形、圆于点E、F
∵BC是⊙O的直径,∴∠BAC=90°
∵ ∴AB=AC,
∵AO=BO ∴AF⊥BC
(1)当⊙O的半径为2时:AC=AB=2
∴S阴影=;
(2)当⊙O的半径为R(R>0)时:AC=AB=R
阴影部分扇形的弧长为:πR
EF=2R-R,以EF为直径作圆,是剩余材料中所作的最大的圆,其圆周长为:(2-)πR
∵πR>(2-)πR
∴不能从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥.
