九年级下册数学第三章圆单元测试三(附答案)
文档属性
| 名称 | 九年级下册数学第三章圆单元测试三(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 324.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-26 21:44:13 | ||
图片预览


文档简介
九年级下册数学第三章圆单元测试三(附答案)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
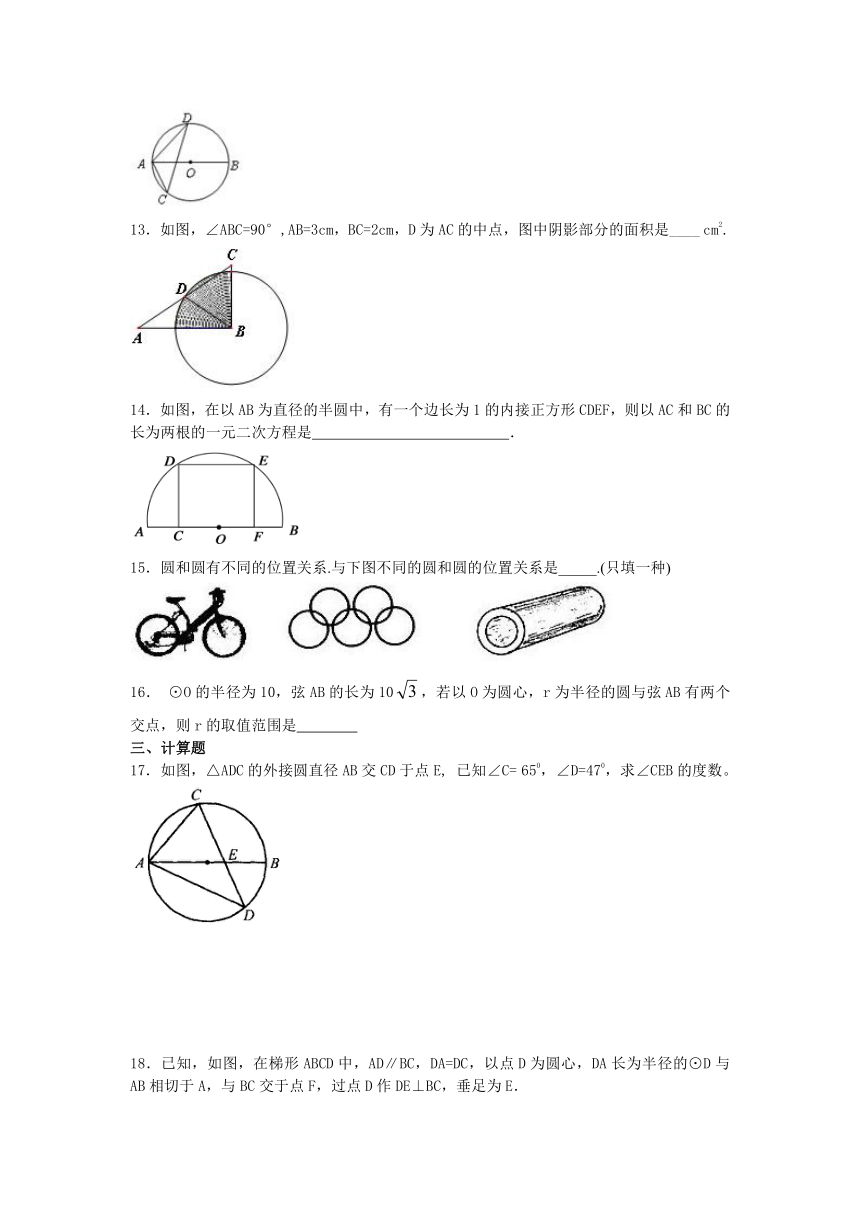
1.如图所示,某产品的商标由三个半径都等于R的圆两两外切得到的图形的一部分,则切点间的弧所围成的阴影部分的面积是( )
(A) (B) (C) (D)
2.已知⊙O1半径为3cm,⊙O2的半径为7cm,若⊙O1和⊙O2的公共点不超过1个,则两圆的圆心距不可能为( )
A.0cm B.4cm C.8cm D.12cm
3.如图,⊙O是等边的外接圆,是⊙O上一点,则等于( )
A. B. C. D.
4.已知P是⊙O内一点,⊙O的半径为15,P点到圆心O的距离为9,则通过P点且长度是整数的弦的条数是( )
A.5 B.7 C.10 D.12
5.如图,C是以AB为直径的⊙O上一点,已知AB=5,BC=3,则圆心O到弦BC的距离是
A. 1.5 B. 2 C. 2.5 D. 3
6.如图,⊙、⊙相内切于点A,其半径分别是8和4,将⊙沿直线平移至两圆相外切时,则点移动的长度是
A.4 B.8 C.16 D.8 或16
7.⊙O1的半径为3厘米,⊙O2的半径为2厘米,圆心距O1O2=5厘米,这两圆的位置关系是( )
A.内含 B.内切 C.相交 D.外切
8. 如图,AB和CD都是⊙O的直径,∠AOC=52°,则∠C的度数是( )
A.22° B.26° C.38° D.48°
9.如图是某几何体的三视图及相关数据,则该几何体的侧面积是
A. 10π B. 15π C. 20π D. 30π
10.已知⊙O1与⊙O2相切 (包括内切与外切 ) ,⊙O1的半径为3 cm ,⊙O2的半径为2 cm,则O1O2的长是( )
A.1 cm B.5 cm C.1 cm或5 cm D.0.5cm或2.5cm
二、填空题
11.小华为参加毕业晚会演出,准备制作一顶圆锥形纸帽,如图所示,纸帽的底面半径为9cm,母线长为30cm,制作这个纸帽的扇形纸板的圆心角为 度.
12.如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=40(,则∠BAD= .
13.如图,∠ABC=90°,AB=3cm,BC=2cm,D为AC的中点,图中阴影部分的面积是____ cm2.
14.如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF,则以AC和BC的长为两根的一元二次方程是 .
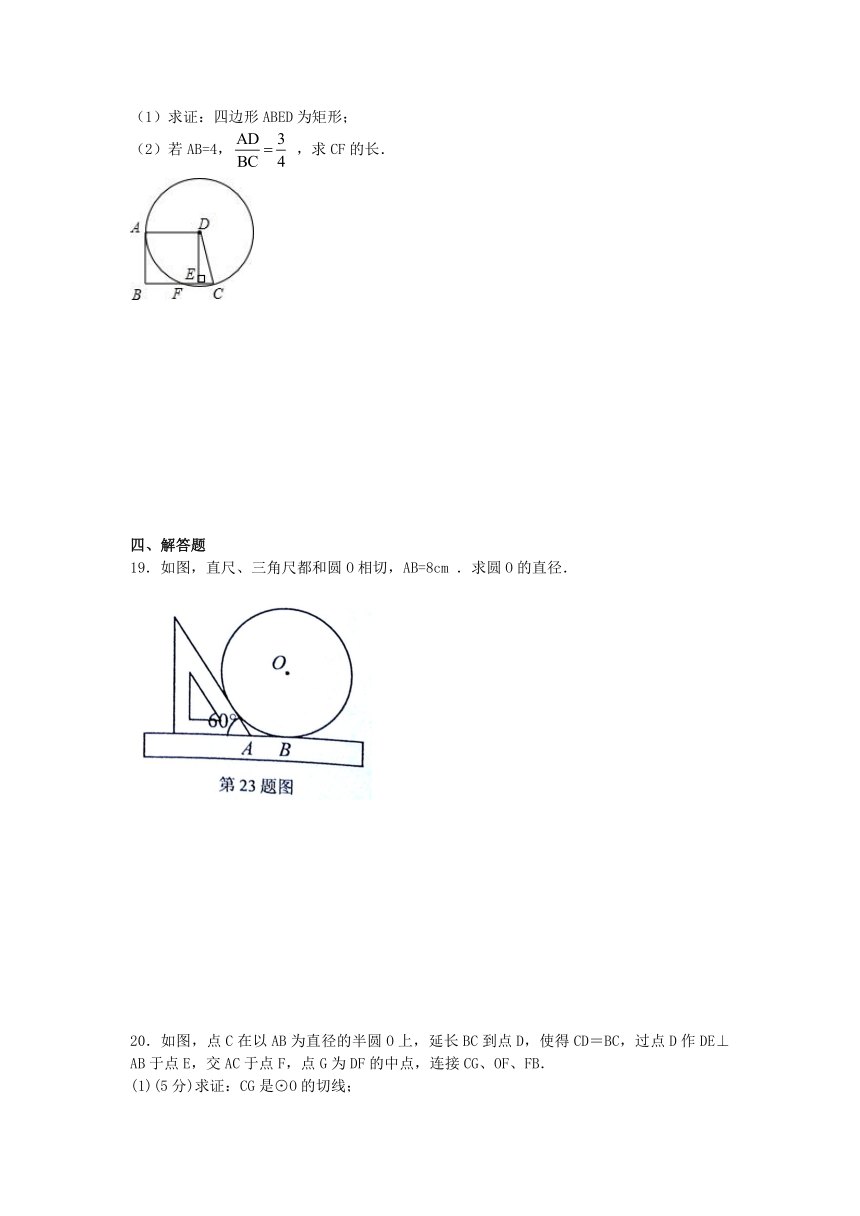
15.圆和圆有不同的位置关系.与下图不同的圆和圆的位置关系是_____.(只填一种)
16. ⊙O的半径为10,弦AB的长为10,若以O为圆心,r为半径的圆与弦AB有两个交点,则r的取值范围是
三、计算题
17.如图,△ADC的外接圆直径AB交CD于点E, 已知∠C= 650,∠D=470,求∠CEB的度数。
18.已知,如图,在梯形ABCD中,AD∥BC,DA=DC,以点D为圆心,DA长为半径的⊙D与AB相切于A,与BC交于点F,过点D作DE⊥BC,垂足为E.
(1)求证:四边形ABED为矩形;
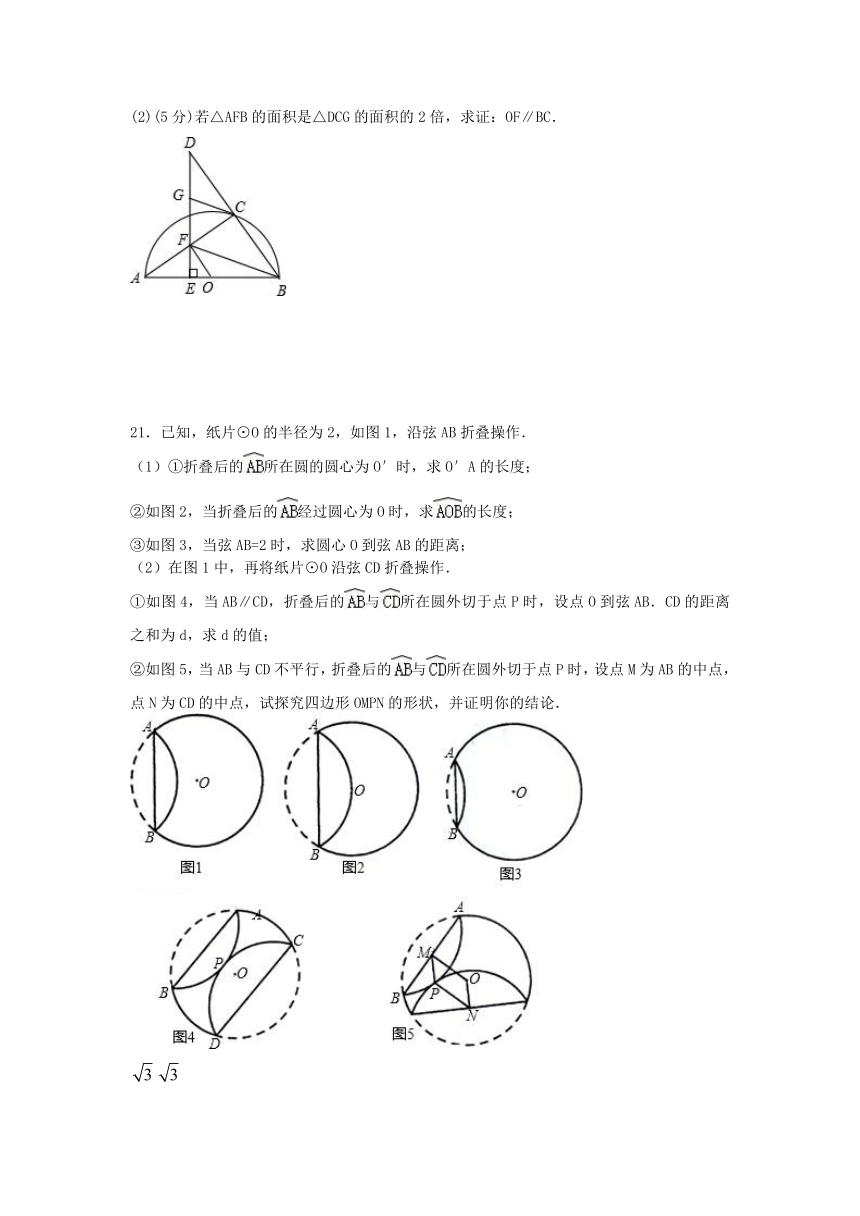
(2)若AB=4, ,求CF的长.
四、解答题
19.如图,直尺、三角尺都和圆O相切,AB=8cm .求圆O的直径.
20.如图,点C在以AB为直径的半圆O上,延长BC到点D,使得CD=BC,过点D作DE⊥AB于点E,交AC于点F,点G为DF的中点,连接CG、OF、FB.
(1)(5分)求证:CG是⊙O的切线;
(2)(5分)若△AFB的面积是△DCG的面积的2倍,求证:OF∥BC.
21.已知,纸片⊙O的半径为2,如图1,沿弦AB折叠操作.
(1)①折叠后的所在圆的圆心为O′时,求O′A的长度;
②如图2,当折叠后的经过圆心为O时,求的长度;
③如图3,当弦AB=2时,求圆心O到弦AB的距离;
(2)在图1中,再将纸片⊙O沿弦CD折叠操作.
①如图4,当AB∥CD,折叠后的与所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
②如图5,当AB与CD不平行,折叠后的与所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
23.如图,已知,两点的坐标分别为(,),(,),⊙的圆心坐标为(,),并与轴交于坐标原点.若是⊙上的一个动点,线段与轴交于点.
(1)线段长度的最小值是_________,最大值是_________;
(2)当点运动到点和点时,线段所在的直线与⊙相切,求由 、、弧所围成的图形的面积;
(3)求出△的最大值和最小值
24.如图,BD是⊙O的直径,过点D的切线交⊙O的弦BC的延长线于点E,弦AC∥DE交BD于点G
(1)求证:BD平分弦AC;
(2)若弦AD=5㎝,AC=8㎝,求⊙O的半径.
25.如图,△ABO中,OA=OB,以O为圆心的圆经过AB的中点C,分别交OA、OB于点E、F。若△ABO腰上的高BD等于底边AB的一半且AB=.
(1)求∠AOB的度数;
(2)求弧ECF的长;
(3)把扇形OEF卷成一个无底的圆锥,则圆锥的底面半径是多少?
参考答案
1.A
2.C
3.C
4.D
5.B
6.D
7.D。
8.B
9.B
10.C
11.108
12.500
13.
14.x2﹣x+1=0
15.相切(内切或外切)
16.5<r≤10
17.连接BC
∵AB为直径,
∴,
又∵,
∴,
∵,
∴.
18.(1)证明见解析(2)2
19.
20.略
21.(1)①2,② ,③(2)①2,②平行四边形,证明略
22.(1)解:由于OA=OB= ,且OD⊥AB,根据垂径定理知圆心D必在y轴上;
连接AD,设⊙D的半径为R,则AD=R,OD=3-R;
Rt△ADO中,根据垂径定理得:
,解得R=2;
即⊙D的半径为2;
(2)证明:过D作DH⊥EN于H,连接MH;
易知四边形DHNO是矩形,则HN=OD=1;
Rt△DHE中,MH是斜边DE的中线,
∴DM=ME=MH=1 2 DE=1;
∴△MEH、△MHN是等腰三角形,即∠MEH=∠MHE=2∠MNE;
∵∠DMH=∠E+∠MHE,故∠DMH=3∠MNE;
(3)解:∵∠DMN=45°,
∴∠MNE=15°,∠E=30°;
Rt△DHE中,DE=2,∠E=30°;
∴DH=1,EH= ;
∴EN=EH+HN= +1;
故E(1, +1),
根据轴对称性可知,点E在第二象限的对称点(-1,+1)也可以.
故点E的坐标为:(1, +1)或(-1, +1).
23.(1) ,(2) (3)最大值为,最小值为
24.(1)证明:∵DE是⊙O的切线,且BD是直径,∴BD⊥DE
又∵AC∥DE ∴BD⊥AC ∴BD平分AC
(2)连结AO; ∵AG=GC,AC=8cm,∴AG=4cm
在Rt△AGD中,由勾股定理得 GD=3cm
设圆的半径为r,则AO=r,OG=r-3
在Rt△AOG中,由勾股定理得 AO2=OG2+AG2
有:r2=(r-3)2+42解得
∴⊙O的半径为cm
25.(1)∵△ABO腰上的高BD等于底边AB的一半
∴∠A=30°
∵OA=OB
∴∠ABO=30°
∴∠AOB=120°
(2)由(1)得∠A=30°
在Rt△ACO中,AC=AB=2,∠A=30°,
则AO=2OC.
由勾股定理,求得OC=2.
∵∠AOB=120°.
由弧长公式可求得的长为π.
(3)r=
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图所示,某产品的商标由三个半径都等于R的圆两两外切得到的图形的一部分,则切点间的弧所围成的阴影部分的面积是( )
(A) (B) (C) (D)
2.已知⊙O1半径为3cm,⊙O2的半径为7cm,若⊙O1和⊙O2的公共点不超过1个,则两圆的圆心距不可能为( )
A.0cm B.4cm C.8cm D.12cm
3.如图,⊙O是等边的外接圆,是⊙O上一点,则等于( )
A. B. C. D.
4.已知P是⊙O内一点,⊙O的半径为15,P点到圆心O的距离为9,则通过P点且长度是整数的弦的条数是( )
A.5 B.7 C.10 D.12
5.如图,C是以AB为直径的⊙O上一点,已知AB=5,BC=3,则圆心O到弦BC的距离是
A. 1.5 B. 2 C. 2.5 D. 3
6.如图,⊙、⊙相内切于点A,其半径分别是8和4,将⊙沿直线平移至两圆相外切时,则点移动的长度是
A.4 B.8 C.16 D.8 或16
7.⊙O1的半径为3厘米,⊙O2的半径为2厘米,圆心距O1O2=5厘米,这两圆的位置关系是( )
A.内含 B.内切 C.相交 D.外切
8. 如图,AB和CD都是⊙O的直径,∠AOC=52°,则∠C的度数是( )
A.22° B.26° C.38° D.48°
9.如图是某几何体的三视图及相关数据,则该几何体的侧面积是
A. 10π B. 15π C. 20π D. 30π
10.已知⊙O1与⊙O2相切 (包括内切与外切 ) ,⊙O1的半径为3 cm ,⊙O2的半径为2 cm,则O1O2的长是( )
A.1 cm B.5 cm C.1 cm或5 cm D.0.5cm或2.5cm
二、填空题
11.小华为参加毕业晚会演出,准备制作一顶圆锥形纸帽,如图所示,纸帽的底面半径为9cm,母线长为30cm,制作这个纸帽的扇形纸板的圆心角为 度.
12.如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=40(,则∠BAD= .
13.如图,∠ABC=90°,AB=3cm,BC=2cm,D为AC的中点,图中阴影部分的面积是____ cm2.
14.如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF,则以AC和BC的长为两根的一元二次方程是 .
15.圆和圆有不同的位置关系.与下图不同的圆和圆的位置关系是_____.(只填一种)
16. ⊙O的半径为10,弦AB的长为10,若以O为圆心,r为半径的圆与弦AB有两个交点,则r的取值范围是
三、计算题
17.如图,△ADC的外接圆直径AB交CD于点E, 已知∠C= 650,∠D=470,求∠CEB的度数。
18.已知,如图,在梯形ABCD中,AD∥BC,DA=DC,以点D为圆心,DA长为半径的⊙D与AB相切于A,与BC交于点F,过点D作DE⊥BC,垂足为E.
(1)求证:四边形ABED为矩形;
(2)若AB=4, ,求CF的长.
四、解答题
19.如图,直尺、三角尺都和圆O相切,AB=8cm .求圆O的直径.
20.如图,点C在以AB为直径的半圆O上,延长BC到点D,使得CD=BC,过点D作DE⊥AB于点E,交AC于点F,点G为DF的中点,连接CG、OF、FB.
(1)(5分)求证:CG是⊙O的切线;
(2)(5分)若△AFB的面积是△DCG的面积的2倍,求证:OF∥BC.
21.已知,纸片⊙O的半径为2,如图1,沿弦AB折叠操作.
(1)①折叠后的所在圆的圆心为O′时,求O′A的长度;
②如图2,当折叠后的经过圆心为O时,求的长度;
③如图3,当弦AB=2时,求圆心O到弦AB的距离;
(2)在图1中,再将纸片⊙O沿弦CD折叠操作.
①如图4,当AB∥CD,折叠后的与所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
②如图5,当AB与CD不平行,折叠后的与所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
23.如图,已知,两点的坐标分别为(,),(,),⊙的圆心坐标为(,),并与轴交于坐标原点.若是⊙上的一个动点,线段与轴交于点.
(1)线段长度的最小值是_________,最大值是_________;
(2)当点运动到点和点时,线段所在的直线与⊙相切,求由 、、弧所围成的图形的面积;
(3)求出△的最大值和最小值
24.如图,BD是⊙O的直径,过点D的切线交⊙O的弦BC的延长线于点E,弦AC∥DE交BD于点G
(1)求证:BD平分弦AC;
(2)若弦AD=5㎝,AC=8㎝,求⊙O的半径.
25.如图,△ABO中,OA=OB,以O为圆心的圆经过AB的中点C,分别交OA、OB于点E、F。若△ABO腰上的高BD等于底边AB的一半且AB=.
(1)求∠AOB的度数;
(2)求弧ECF的长;
(3)把扇形OEF卷成一个无底的圆锥,则圆锥的底面半径是多少?
参考答案
1.A
2.C
3.C
4.D
5.B
6.D
7.D。
8.B
9.B
10.C
11.108
12.500
13.
14.x2﹣x+1=0
15.相切(内切或外切)
16.5<r≤10
17.连接BC
∵AB为直径,
∴,
又∵,
∴,
∵,
∴.
18.(1)证明见解析(2)2
19.
20.略
21.(1)①2,② ,③(2)①2,②平行四边形,证明略
22.(1)解:由于OA=OB= ,且OD⊥AB,根据垂径定理知圆心D必在y轴上;
连接AD,设⊙D的半径为R,则AD=R,OD=3-R;
Rt△ADO中,根据垂径定理得:
,解得R=2;
即⊙D的半径为2;
(2)证明:过D作DH⊥EN于H,连接MH;
易知四边形DHNO是矩形,则HN=OD=1;
Rt△DHE中,MH是斜边DE的中线,
∴DM=ME=MH=1 2 DE=1;
∴△MEH、△MHN是等腰三角形,即∠MEH=∠MHE=2∠MNE;
∵∠DMH=∠E+∠MHE,故∠DMH=3∠MNE;
(3)解:∵∠DMN=45°,
∴∠MNE=15°,∠E=30°;
Rt△DHE中,DE=2,∠E=30°;
∴DH=1,EH= ;
∴EN=EH+HN= +1;
故E(1, +1),
根据轴对称性可知,点E在第二象限的对称点(-1,+1)也可以.
故点E的坐标为:(1, +1)或(-1, +1).
23.(1) ,(2) (3)最大值为,最小值为
24.(1)证明:∵DE是⊙O的切线,且BD是直径,∴BD⊥DE
又∵AC∥DE ∴BD⊥AC ∴BD平分AC
(2)连结AO; ∵AG=GC,AC=8cm,∴AG=4cm
在Rt△AGD中,由勾股定理得 GD=3cm
设圆的半径为r,则AO=r,OG=r-3
在Rt△AOG中,由勾股定理得 AO2=OG2+AG2
有:r2=(r-3)2+42解得
∴⊙O的半径为cm
25.(1)∵△ABO腰上的高BD等于底边AB的一半
∴∠A=30°
∵OA=OB
∴∠ABO=30°
∴∠AOB=120°
(2)由(1)得∠A=30°
在Rt△ACO中,AC=AB=2,∠A=30°,
则AO=2OC.
由勾股定理,求得OC=2.
∵∠AOB=120°.
由弧长公式可求得的长为π.
(3)r=
