九年级下册数学第三章圆单元测试十二(附答案)
文档属性
| 名称 | 九年级下册数学第三章圆单元测试十二(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 227.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-26 00:00:00 | ||
图片预览



文档简介
九年级下册数学第三章圆单元测试十二(附答案)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.定圆O的半径是4cm,动圆P的半径是2cm,动圆在直线l上移动,当两圆相切时,OP的值是( )
A.2cm或6cm B.2cm C.4cm D.6cm
2.如图、在Rt△ABC中,∠C=90°,AC=8,BC=6,两等圆⊙A,⊙B外切,那么图中两个扇形(即
阴影部分)的面积之和为( )
A. B. C. D.
3.如图,是的切线,切点为A,PA=2,∠APO=30°,则的半径为
A.1 B. C.2 D.4
4.已知两圆的半径分别为3cm和2cm,圆心距为5cm,则两圆的位置关系是
A.相交 B.外切 C.内切 D.外离
5.时钟分针的长10㎝,经过45分钟,它的针尖转过的路程是 ( )
(A)㎝ (B)15㎝ (C)㎝ (D)75㎝
6.一个圆锥的侧面积是底面积的2倍。则圆锥侧面展开图的扇形的圆心角是( )
A .1200 B.1800 C.2400 D.3000
7. 小刚用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10cm,那么这张扇形纸板的面积是( )
A.120πcm2 B.240πcm2 C.260πcm2 D.480πcm2
8.已知相交两圆的半径分别为4和7,则它们的圆心距可能是 ( )
A. 2 B. 3 C. 6 D. 11
9.用半径为2cm的半圆围成一个圆锥的侧面,这个圆锥的底面半径为( )
A.1cm B.2cm C.πcm D.2πcm
10.圆锥的底面半径为r,母线为l,当r=1, l=3时,圆锥的侧面展开的扇形面积为( )
A. B. C. D.
二、填空题
11.已知⊙P的半径为2,圆心P在抛物线上运动,当⊙P与轴相切时,圆心P的坐标为 .
12.根据“不在同一直线上的三点确定一个圆”,可以判断平面直角坐标系内的三个点A(3,0)、B(0,-4)、C(2,-3) 确定一个圆(填“能”或“不能”)。
13.如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,那么Δ PDE的周长为
14.如图,在Rt△ABC中,∠C=90°,CA=CB=2。分别以A、B、C为圆心,以AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是______.
15.已知梯形ABCD内接于⊙O,AB//CD,AB=8 cm,CD =6 cm,⊙O的半径为5cm,则S梯形ABCD=
16.圆锥的母线长为6cm,侧面展开图是圆心角为300(的扇形,则圆锥底面半径为 cm,
三、计算题
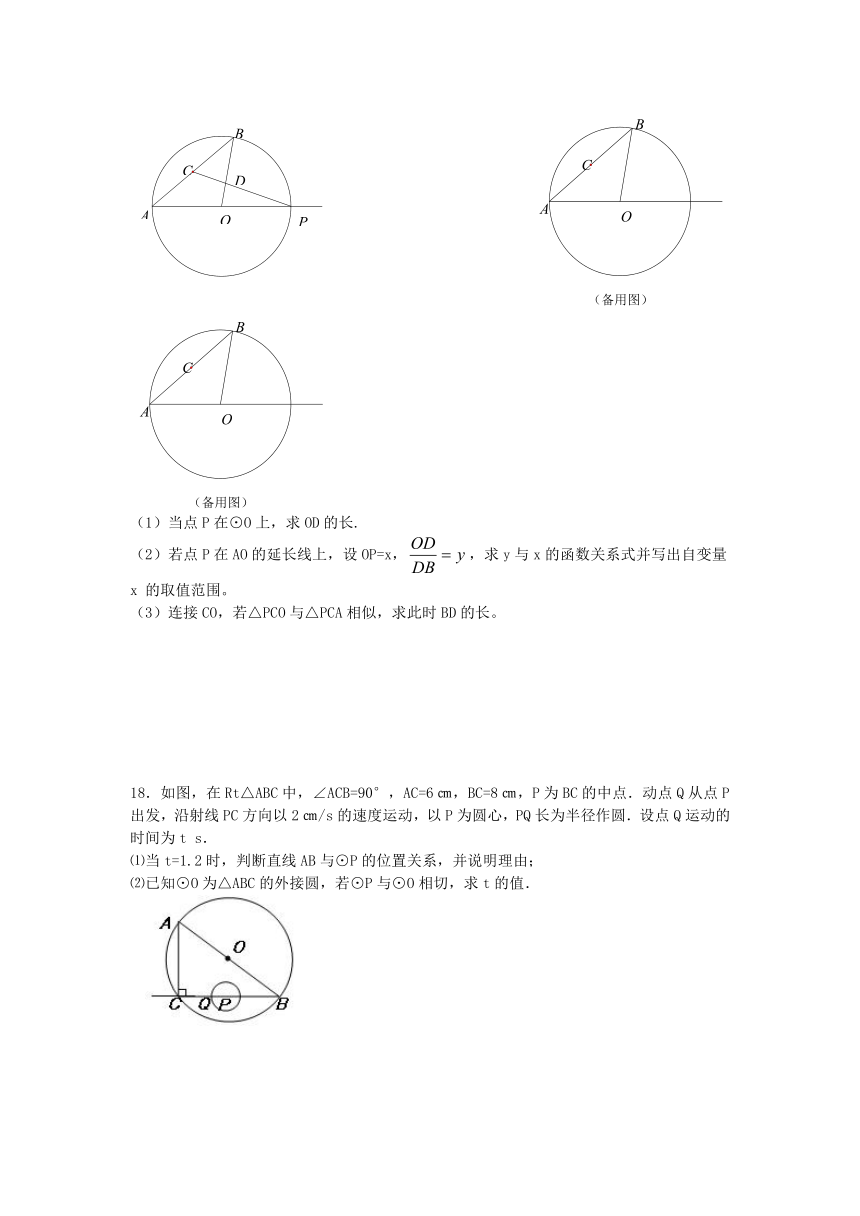
17.已知:⊙O的半径OA=5,弦AB=8,C是弦AB的中点,点P是射线AO上一点(与点A不重合),直线PC与射线BO交于点D.
(1)当点P在⊙O上,求OD的长.
(2)若点P在AO的延长线上,设OP=x,,求y与x的函数关系式并写出自变量x 的取值范围。
(3)连接CO,若△PCO与△PCA相似,求此时BD的长。
18.如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
⑴当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
⑵已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.
四、解答题
19.(1)按语句作图并回答:
作线段AC(AC=4),以A为圆心a为半径作圆,再以C为圆心b为半径作圆(,,圆A与圆C交于B、D两点),连结AB、BC、CD、DA.若能作出满足要求的四边形ABCD,则应满足什么条件?
(2)若,求四边形ABCD的面积.
20.在平面直角坐标系xOy中,已知动点P在正比例函数y=x的图象上,点P的横坐标为m(m>0)。以点P为圆心,为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(D点在点C的上方)。点E为平行四边形DOPE的顶点(如图)。
(1)写出点B、E的坐标(用含m的代数式表示);
(2)连接DB、BE,设△BDE的外接圆交y轴于点Q(点Q异于点D),连接EQ、BQ。试问线段BQ与线段EQ的长是否相等?为什么?
(3)连接BC,求∠DBC-∠DBE的度数。
21.如图,分别与相切于点,点在上,且,,垂足为.
(1)求证:;
(2)若的半径,,求的长
22.如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A(0,2),B(4,2)C(6,0),解答下列问题:
请在图中确定该圆弧所在圆心D点的位置,则D点坐标为________ ;
连结AD,CD,求⊙D的半径(结果保留根号);
求扇形DAC的面积. (结果保留π)
23.如图,已知:△ABC是⊙O的内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°.
(1)判断直线CD与⊙O的位置关系,并说明理由.
(2)若AC=6,求图中弓形(即阴影部分)的面积.
24.如图,点在圆O上,,与相交于点,,延长到点,使,连结.求证:直线与圆O相切.
25.如图,在Rt△ABC中,已知∠ABC=90°,BC=8,以AB为直径作⊙O,连结OC,过点C作⊙O的切线CD,D为切点,若sin∠OCD=,求直径AB的长.
参考答案
1.A
2.B
3.C
4.B
5.B
6.B
7.B
8.C
9.A。
10.B
11.
12.能
13.16cm
14.
15.49cm2或7cm2
16.5
17.解:当P在⊙O上时,连接BP
∵ C是AB中点,O是AP中点,
∴ 点D为△ABP的重心, ∴
∵ OA=OB=5 ∴
(2)过点O作OE//AB,交PC于点E(如图)
∵OE//AB ∴,
又∵ AC=BC ∴
即 (x>0)
(3) 当P在AO延长线上时,若△PCO∽△PAC时,有∠PCO=∠A,
∵∠A=∠B,∴∠PCO=∠B, 易证△ACO∽△BDC
得 得 ∴
当P在AO上时,若△PCO∽△PAC时,可得CP⊥AO(如图)
作BH⊥AO,可求得 ,
由, 得 ∴
则
综上所述,若△PCO与△PCA相似,此时BD的长为或
18.解:⑴直线与⊙P相切.
如图,过点P作PD⊥AB, 垂足为D.
在Rt△ABC中,∠ACB=90°,∵AC=6cm,BC=8cm,
∴.∵P为BC的中点,∴PB=4cm.
∵∠PDB=∠ACB=90°,∠PBD=∠ABC.∴△PBD∽△ABC.
∴,即,∴PD =2.4(cm) .
当时,(cm)
∴,即圆心到直线的距离等于⊙P的半径.
∴直线与⊙P相切.
⑵ ∠ACB=90°,∴AB为△ABC的外切圆的直径.∴.
连接OP.∵P为BC的中点,∴.
∵点P在⊙O内部,∴⊙P与⊙O只能内切.
∴或,∴=1或4.
∴⊙P与⊙O相切时,t的值为1或4.
19.(1) (2)
20.(1)B(3m,0),E(m,4m)(2)线段BQ与线段EQ的长相等(3)450
21.(1)略(2)5
22.解:(1)连接AB、BC,
作它们的垂直平分线的交点就是圆心的位置,
从图中可以看出它的坐标.
D点坐标(2.5,-1);
(2)在直角三角形ADF中,根据勾股定理可得
⊙D半径为0.5 ;
(3)扇形的圆心角是90度.
所以扇形DAC面积为=.
23.(1)直线CD是⊙O的切线,(2)6π-9
24.连OA,如图,
∵AE=ED,FB=BD,
∴AE:ED=FB:BD,
∴BE∥AF,
又∵AB=AC,
∴弧AB=弧AC,
∴OA⊥BC,
∴OA⊥AF,
∴直线AF与⊙O相切.
25.直径AB=12.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.定圆O的半径是4cm,动圆P的半径是2cm,动圆在直线l上移动,当两圆相切时,OP的值是( )
A.2cm或6cm B.2cm C.4cm D.6cm
2.如图、在Rt△ABC中,∠C=90°,AC=8,BC=6,两等圆⊙A,⊙B外切,那么图中两个扇形(即
阴影部分)的面积之和为( )
A. B. C. D.
3.如图,是的切线,切点为A,PA=2,∠APO=30°,则的半径为
A.1 B. C.2 D.4
4.已知两圆的半径分别为3cm和2cm,圆心距为5cm,则两圆的位置关系是
A.相交 B.外切 C.内切 D.外离
5.时钟分针的长10㎝,经过45分钟,它的针尖转过的路程是 ( )
(A)㎝ (B)15㎝ (C)㎝ (D)75㎝
6.一个圆锥的侧面积是底面积的2倍。则圆锥侧面展开图的扇形的圆心角是( )
A .1200 B.1800 C.2400 D.3000
7. 小刚用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10cm,那么这张扇形纸板的面积是( )
A.120πcm2 B.240πcm2 C.260πcm2 D.480πcm2
8.已知相交两圆的半径分别为4和7,则它们的圆心距可能是 ( )
A. 2 B. 3 C. 6 D. 11
9.用半径为2cm的半圆围成一个圆锥的侧面,这个圆锥的底面半径为( )
A.1cm B.2cm C.πcm D.2πcm
10.圆锥的底面半径为r,母线为l,当r=1, l=3时,圆锥的侧面展开的扇形面积为( )
A. B. C. D.
二、填空题
11.已知⊙P的半径为2,圆心P在抛物线上运动,当⊙P与轴相切时,圆心P的坐标为 .
12.根据“不在同一直线上的三点确定一个圆”,可以判断平面直角坐标系内的三个点A(3,0)、B(0,-4)、C(2,-3) 确定一个圆(填“能”或“不能”)。
13.如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,那么Δ PDE的周长为
14.如图,在Rt△ABC中,∠C=90°,CA=CB=2。分别以A、B、C为圆心,以AC为半径画弧,三条弧与边AB所围成的阴影部分的面积是______.
15.已知梯形ABCD内接于⊙O,AB//CD,AB=8 cm,CD =6 cm,⊙O的半径为5cm,则S梯形ABCD=
16.圆锥的母线长为6cm,侧面展开图是圆心角为300(的扇形,则圆锥底面半径为 cm,
三、计算题
17.已知:⊙O的半径OA=5,弦AB=8,C是弦AB的中点,点P是射线AO上一点(与点A不重合),直线PC与射线BO交于点D.
(1)当点P在⊙O上,求OD的长.
(2)若点P在AO的延长线上,设OP=x,,求y与x的函数关系式并写出自变量x 的取值范围。
(3)连接CO,若△PCO与△PCA相似,求此时BD的长。
18.如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
⑴当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
⑵已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.
四、解答题
19.(1)按语句作图并回答:
作线段AC(AC=4),以A为圆心a为半径作圆,再以C为圆心b为半径作圆(,,圆A与圆C交于B、D两点),连结AB、BC、CD、DA.若能作出满足要求的四边形ABCD,则应满足什么条件?
(2)若,求四边形ABCD的面积.
20.在平面直角坐标系xOy中,已知动点P在正比例函数y=x的图象上,点P的横坐标为m(m>0)。以点P为圆心,为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(D点在点C的上方)。点E为平行四边形DOPE的顶点(如图)。
(1)写出点B、E的坐标(用含m的代数式表示);
(2)连接DB、BE,设△BDE的外接圆交y轴于点Q(点Q异于点D),连接EQ、BQ。试问线段BQ与线段EQ的长是否相等?为什么?
(3)连接BC,求∠DBC-∠DBE的度数。
21.如图,分别与相切于点,点在上,且,,垂足为.
(1)求证:;
(2)若的半径,,求的长
22.如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A(0,2),B(4,2)C(6,0),解答下列问题:
请在图中确定该圆弧所在圆心D点的位置,则D点坐标为________ ;
连结AD,CD,求⊙D的半径(结果保留根号);
求扇形DAC的面积. (结果保留π)
23.如图,已知:△ABC是⊙O的内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°.
(1)判断直线CD与⊙O的位置关系,并说明理由.
(2)若AC=6,求图中弓形(即阴影部分)的面积.
24.如图,点在圆O上,,与相交于点,,延长到点,使,连结.求证:直线与圆O相切.
25.如图,在Rt△ABC中,已知∠ABC=90°,BC=8,以AB为直径作⊙O,连结OC,过点C作⊙O的切线CD,D为切点,若sin∠OCD=,求直径AB的长.
参考答案
1.A
2.B
3.C
4.B
5.B
6.B
7.B
8.C
9.A。
10.B
11.
12.能
13.16cm
14.
15.49cm2或7cm2
16.5
17.解:当P在⊙O上时,连接BP
∵ C是AB中点,O是AP中点,
∴ 点D为△ABP的重心, ∴
∵ OA=OB=5 ∴
(2)过点O作OE//AB,交PC于点E(如图)
∵OE//AB ∴,
又∵ AC=BC ∴
即 (x>0)
(3) 当P在AO延长线上时,若△PCO∽△PAC时,有∠PCO=∠A,
∵∠A=∠B,∴∠PCO=∠B, 易证△ACO∽△BDC
得 得 ∴
当P在AO上时,若△PCO∽△PAC时,可得CP⊥AO(如图)
作BH⊥AO,可求得 ,
由, 得 ∴
则
综上所述,若△PCO与△PCA相似,此时BD的长为或
18.解:⑴直线与⊙P相切.
如图,过点P作PD⊥AB, 垂足为D.
在Rt△ABC中,∠ACB=90°,∵AC=6cm,BC=8cm,
∴.∵P为BC的中点,∴PB=4cm.
∵∠PDB=∠ACB=90°,∠PBD=∠ABC.∴△PBD∽△ABC.
∴,即,∴PD =2.4(cm) .
当时,(cm)
∴,即圆心到直线的距离等于⊙P的半径.
∴直线与⊙P相切.
⑵ ∠ACB=90°,∴AB为△ABC的外切圆的直径.∴.
连接OP.∵P为BC的中点,∴.
∵点P在⊙O内部,∴⊙P与⊙O只能内切.
∴或,∴=1或4.
∴⊙P与⊙O相切时,t的值为1或4.
19.(1) (2)
20.(1)B(3m,0),E(m,4m)(2)线段BQ与线段EQ的长相等(3)450
21.(1)略(2)5
22.解:(1)连接AB、BC,
作它们的垂直平分线的交点就是圆心的位置,
从图中可以看出它的坐标.
D点坐标(2.5,-1);
(2)在直角三角形ADF中,根据勾股定理可得
⊙D半径为0.5 ;
(3)扇形的圆心角是90度.
所以扇形DAC面积为=.
23.(1)直线CD是⊙O的切线,(2)6π-9
24.连OA,如图,
∵AE=ED,FB=BD,
∴AE:ED=FB:BD,
∴BE∥AF,
又∵AB=AC,
∴弧AB=弧AC,
∴OA⊥BC,
∴OA⊥AF,
∴直线AF与⊙O相切.
25.直径AB=12.
