无理数
图片预览





文档简介
课件15张PPT。 然而,第一个发现这样的数的人却被抛进大海,你想知道这其中的曲折离奇吗?这得追溯到2500年前,有个叫毕达哥拉斯的人,他是一个伟大的数学家,他创立了毕达哥拉斯学派,这是一个非常神秘的学派,他们以领袖毕达哥拉斯为核心,认为毕达哥拉斯是至高无尚的,他所说的一切都是真理。
毕达哥拉斯( Pythagoras) 认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述
了解无理数的历史 但后来,这学派的一位年轻成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,他们试图封锁这一发现,然而希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,在他逃回家的路上,遭到毕氏成员的围捕,被投入大海。
他这一死,使得这类数的计算推迟了500多年,给数学的发展造成了不可弥补的损失。
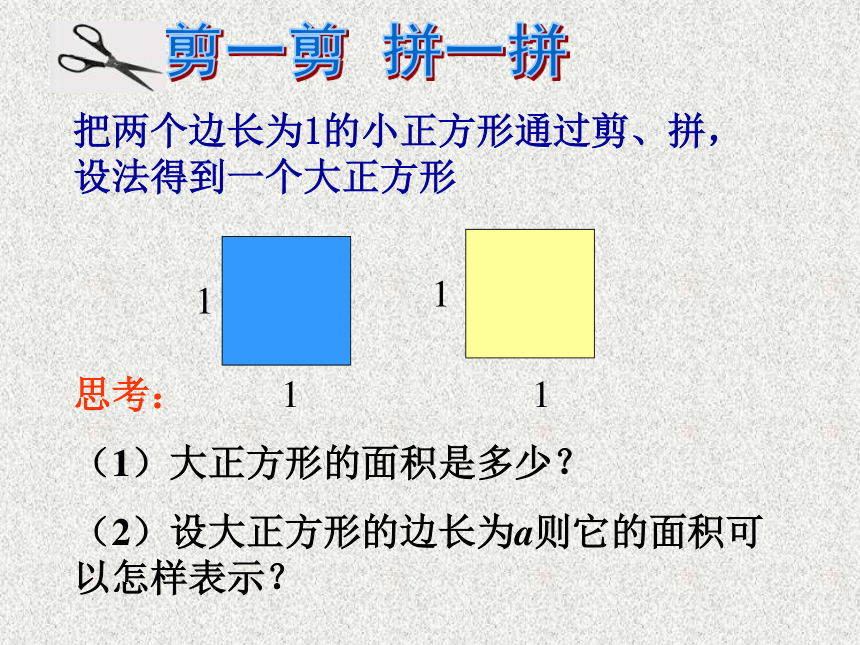
把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形剪一剪 拼一拼思考:
(1)大正方形的面积是多少?
(2)设大正方形的边长为a则它的面积可以怎样表示? 剪一剪,拼一拼议一议
(1)a可能是整数吗?说说你的理由。
(2)a可能是以2为分母的分数吗?可能是以3为分母的分数吗?说说你的理由。
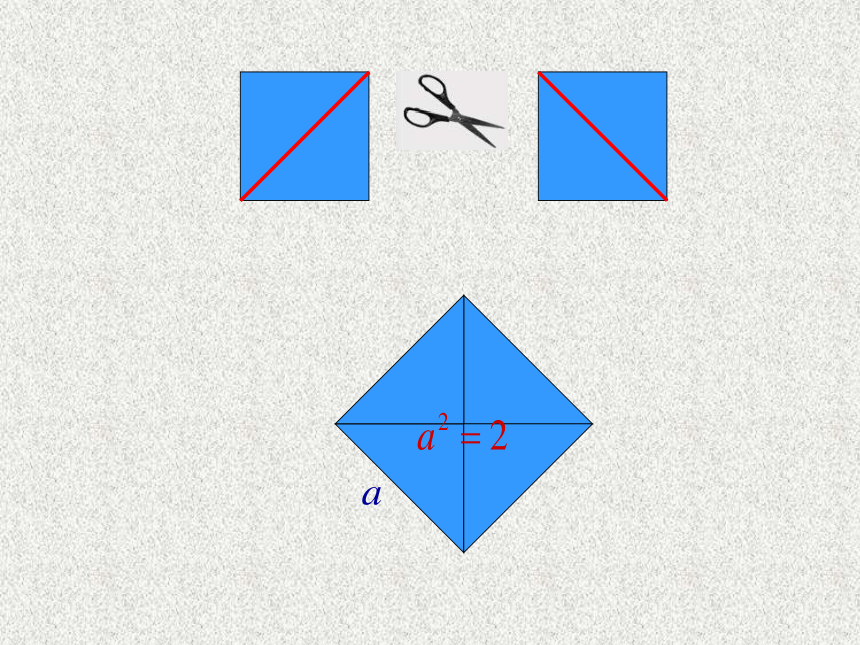
(3)a可能是分数吗?说说你的理由,并与同伴交流。面积为2的正方形的边长a究竟是多少呢?思考:
(1)三个正方形的边长之间有怎样的大小关系?
(2)边长a的整数部分是几?十分位是几?百分位是几?千分位呢?用计算器进行探索。
(3)a可能是有限小数吗?
11它是一个无限不循环小数=1.41421356…无限不循小数叫做无理数。例:下列各数中,哪些是有理数?哪些是无理数? ·
-π,-3.14, 1.732,0.03,18,0.484848 ……,0.3131131113…… (两个3之间依次多一个1)
解: ·
有理数{ … }
无理数{ … }-3.14, 1.732,0.03,18,0.484848 …,-π, 0.3131131113…,练习一:
A组:下列各数中,哪些是有理数?哪些是无理数? ·
-1, 0.1, π,0.301230123012……,2.3020020002…
B组:下列说法对不对?如果不对,请说明理由。
⑴无限小数都是无理数
⑵无理数都是无限小数
⑶不循环小数是无理数
⑷面积为3的正方形的边长是无理数 练习二:
A组:1、下列各数中,哪些是有理数?哪些是无理数? B组:0.304, - 2 π, 0 ,-5,0.1212212221…(两个1之间依次多1个2)b是无理数吗?如果是请
用计算器探索b的近似值
(探索到0.001)2、用计算器探索面积为3的正方形的边长。(探索到十分位)小结:谈谈你这节课的收获螺形图欣赏有趣的图形:A组:课本44页随堂练习及习题第一题
B组:课本42页试一试及45页第二题作业
毕达哥拉斯( Pythagoras) 认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述
了解无理数的历史 但后来,这学派的一位年轻成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,他们试图封锁这一发现,然而希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,在他逃回家的路上,遭到毕氏成员的围捕,被投入大海。
他这一死,使得这类数的计算推迟了500多年,给数学的发展造成了不可弥补的损失。
把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形剪一剪 拼一拼思考:
(1)大正方形的面积是多少?
(2)设大正方形的边长为a则它的面积可以怎样表示? 剪一剪,拼一拼议一议
(1)a可能是整数吗?说说你的理由。
(2)a可能是以2为分母的分数吗?可能是以3为分母的分数吗?说说你的理由。
(3)a可能是分数吗?说说你的理由,并与同伴交流。面积为2的正方形的边长a究竟是多少呢?思考:
(1)三个正方形的边长之间有怎样的大小关系?
(2)边长a的整数部分是几?十分位是几?百分位是几?千分位呢?用计算器进行探索。
(3)a可能是有限小数吗?
11它是一个无限不循环小数=1.41421356…无限不循小数叫做无理数。例:下列各数中,哪些是有理数?哪些是无理数? ·
-π,-3.14, 1.732,0.03,18,0.484848 ……,0.3131131113…… (两个3之间依次多一个1)
解: ·
有理数{ … }
无理数{ … }-3.14, 1.732,0.03,18,0.484848 …,-π, 0.3131131113…,练习一:
A组:下列各数中,哪些是有理数?哪些是无理数? ·
-1, 0.1, π,0.301230123012……,2.3020020002…
B组:下列说法对不对?如果不对,请说明理由。
⑴无限小数都是无理数
⑵无理数都是无限小数
⑶不循环小数是无理数
⑷面积为3的正方形的边长是无理数 练习二:
A组:1、下列各数中,哪些是有理数?哪些是无理数? B组:0.304, - 2 π, 0 ,-5,0.1212212221…(两个1之间依次多1个2)b是无理数吗?如果是请
用计算器探索b的近似值
(探索到0.001)2、用计算器探索面积为3的正方形的边长。(探索到十分位)小结:谈谈你这节课的收获螺形图欣赏有趣的图形:A组:课本44页随堂练习及习题第一题
B组:课本42页试一试及45页第二题作业
