青岛版九年级数学下册 5.4二次函数的图象和性质(第1课时)课件 (共22张PPT)
文档属性
| 名称 | 青岛版九年级数学下册 5.4二次函数的图象和性质(第1课时)课件 (共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-06 07:07:37 | ||
图片预览



文档简介
(共22张PPT)
5.4 二次函数的图象和性质
第1课时
1.知道二次函数的图象是抛物线;
2.会画y=ax2的图象,并能结合图象理解y=ax2的性质.
一次函数的图象是一条直线,反比例函数的图象是双曲线,二次函数的图象是什么形状呢?通常怎样画一个函数的图象?
思考
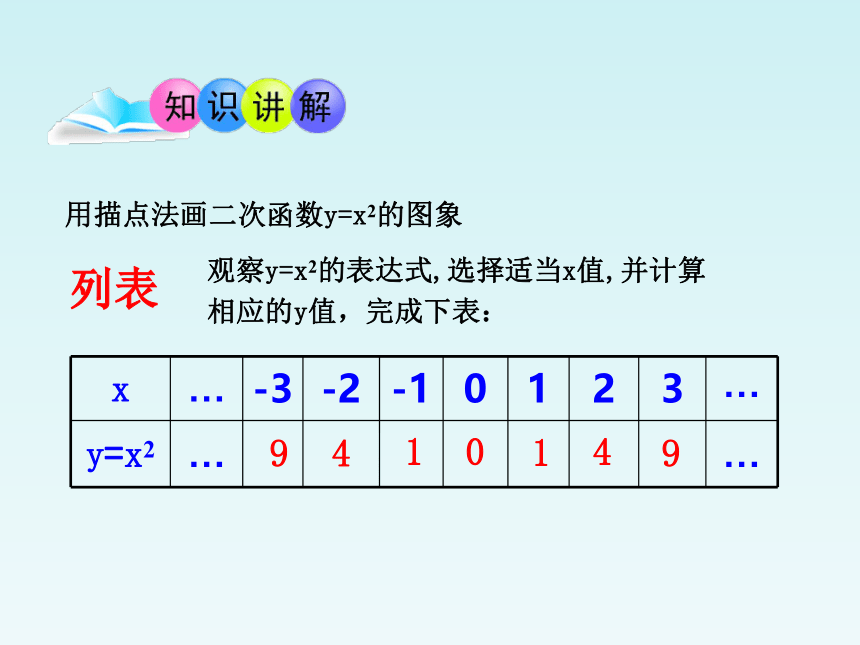
用描点法画二次函数y=x2的图象
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
9
4
1
1
0
4
9
观察y=x2的表达式,选择适当x值,并计算
相应的y值,完成下表:
x
y
0
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
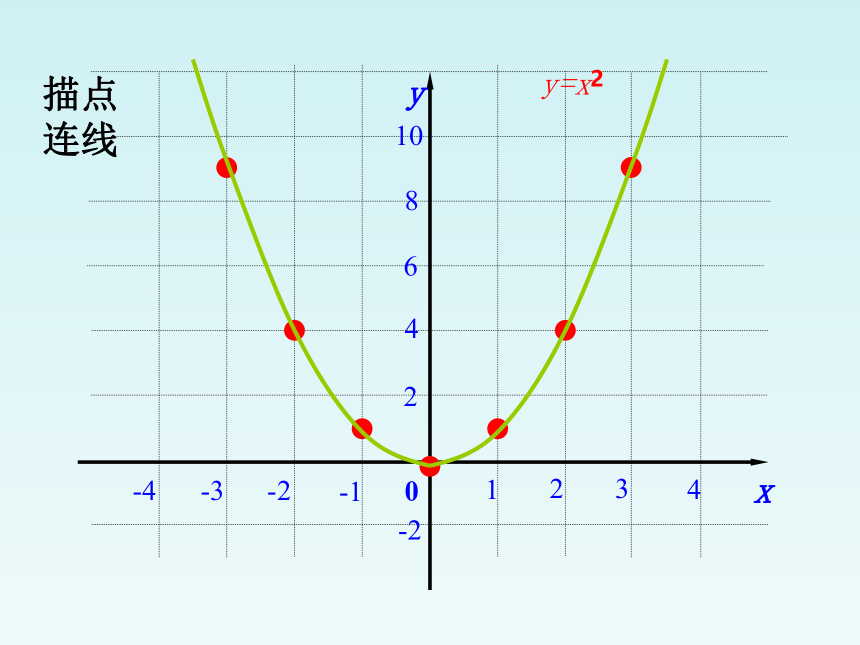
描点
连线
y=x2
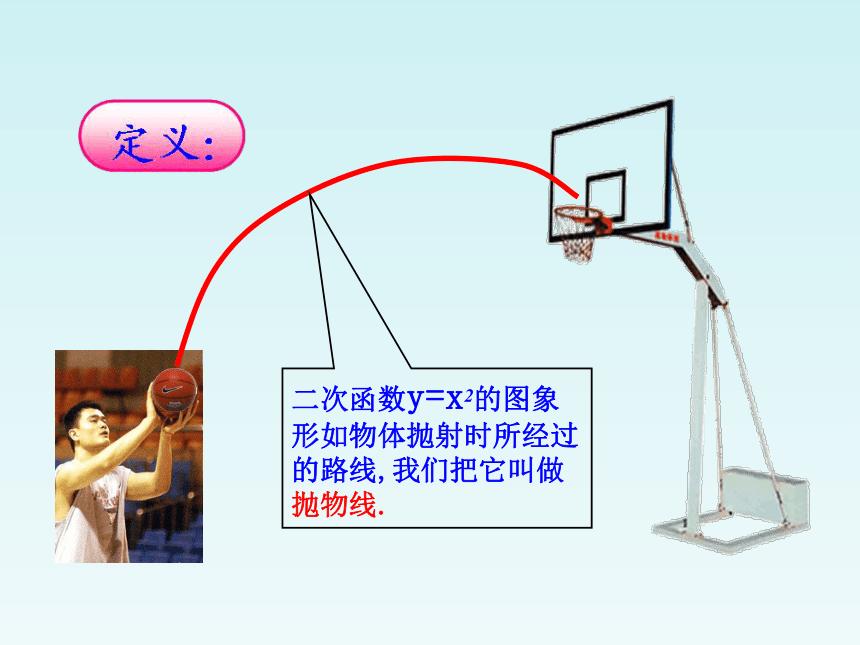
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.
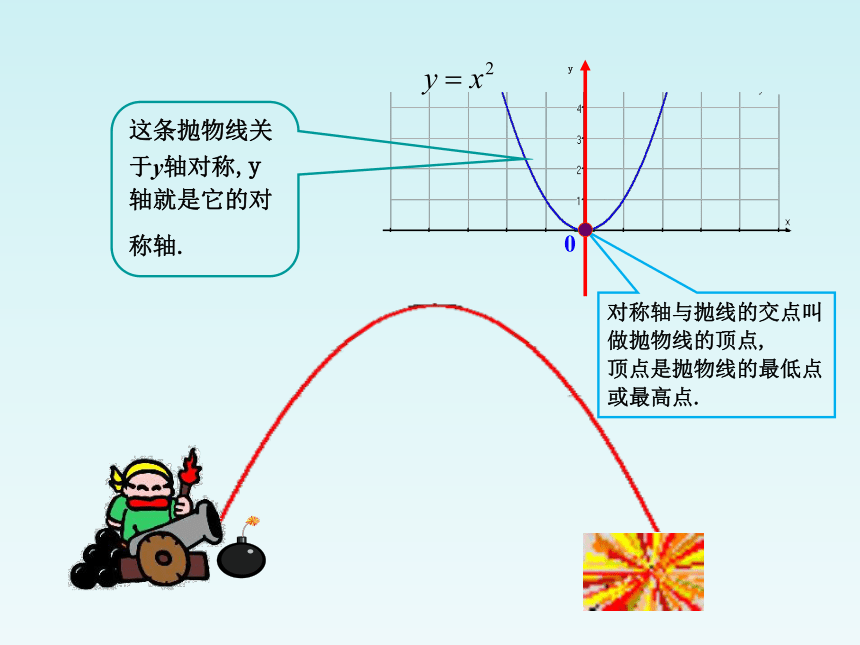
这条抛物线关于y轴对称,y轴就是它的对称轴.
对称轴与抛线的交点叫做抛物线的顶点,
顶点是抛物线的最低点或最高点.
y
0
x
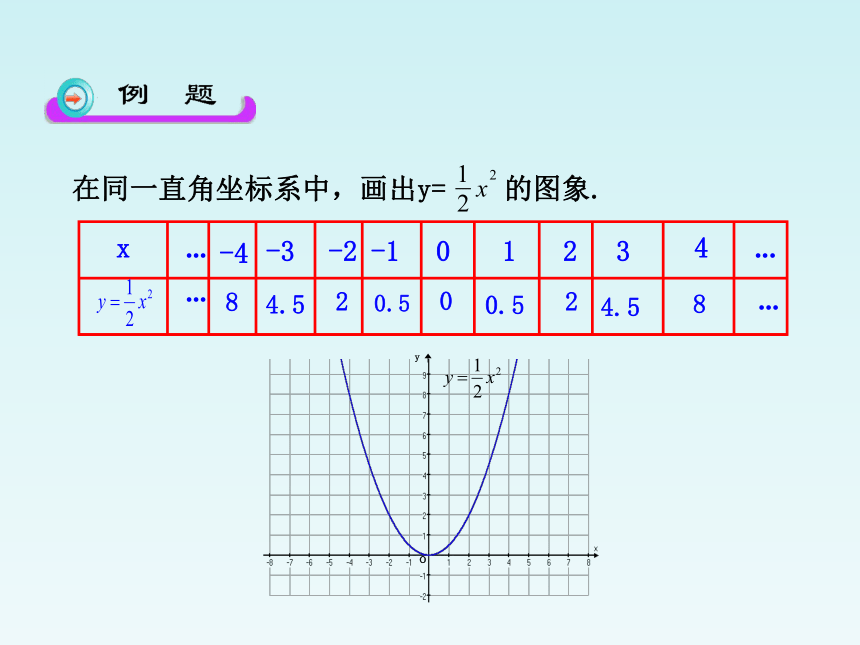
...
...
...
...
0
-4
-3
-2
-1
2
3
1
4
0
0.5
2
4.5
8
0.5
2
4.5
8
在同一直角坐标系中,画出y= 的图象.
y
o
2
2
1
x
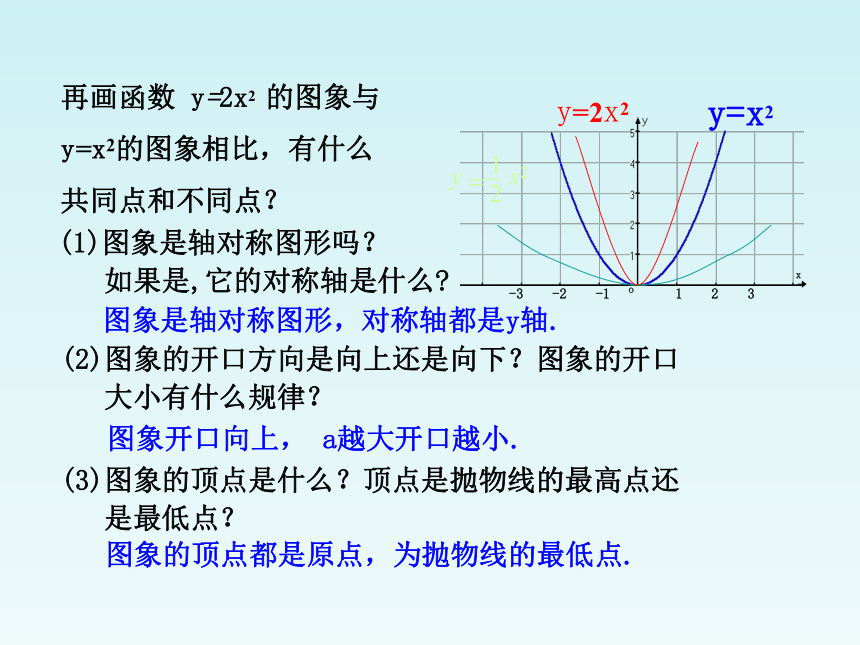
再画函数 y=2x2 的图象与y=x2的图象相比,有什么共同点和不同点?
y=2x2
y=x2
(1)图象是轴对称图形吗?
如果是,它的对称轴是什么
x
o
图象是轴对称图形,对称轴都是y轴.
图象开口向上, a越大开口越小.
图象的顶点都是原点,为抛物线的最低点.
(2)图象的开口方向是向上还是向下?图象的开口
大小有什么规律?
(3)图象的顶点是什么?顶点是抛物线的最高点还
是最低点?
-3 -2 -1 1 2 3
1
2
x2
=
y
当a>0时,抛物线y=ax2的对称轴是y轴,顶点是原点,开
口向上,顶点是抛物线的最低点,a越大,抛物线的开口越小.
(1)二次函数 y = - x2 的图象是什么形状?
你能根据表格中的数据作出猜想吗?
(2)先想一想,然后作出它的图象.
(3)它与二次函数y=x2的图象有什么关系?
x … -3 -2 -1 0 1 2 3 …
y=-x2
在“做”中“学”
… -9 -4 -1 0 -1 -4 -9 …
x
y
0
-4
-3
-2
1
2
3
4
-4
-2
-1
y=-x2
-1
-3
1
描点,连线
二次函数y= -x2 的图象是抛物线.
二次函数y= -x2 的图象与y= x2 的图象关于x轴对称,顶点都为原点,但原点是二次函数y= -x2的最高点,却是 y= x2 的最低点.
请同学们在同一坐标系内画出y= - 0.5x2,y = -2x2的图象,并考虑这些抛物线有什么共同点和不同点.主要从以下几个方面考虑:
1.开口方向
2.开口大小
3.对称轴
4.顶点坐标
5.有最高点还是有最低点
(1)抛物线y=ax2与y= - ax2(a>0)关于__轴对称;
(2)当a>0时,开口_____,顶点是抛物线的最___点;
当a<0时,开口_____,顶点是抛物线的最___点;
(3)︱a︱越大,抛物线的开口_____.
【点拨】a决定了抛物线y=ax2的开口大小和方向.
x
向上
低
向下
高
越小
【规律总结】
二次函数y=ax2的“两关系四对等”
1.a>0 开口向上 有最小值
2.a<0 开口向下 有最大值
1.物体从某一高度落下,已知下落的高度h(m)和下落的时间t(s)的关系式是:h=4.9t2,h是t的 函数,它的图象的 顶点坐标是 .
2.已知抛物线y=ax2经过点A(-2,-8).
(1)求此抛物线的函数解析式.
(2)判断点B(-1,-4)是否在此抛物线上.
(3)求出此抛物线上纵坐标为-6的点的坐标.
(0,0)
二次
y = -2x2
不在抛物线上
3.如图,在四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
解析:选C.如图,作∠CAE=90°,作DE⊥AE于E,作DF⊥AC于F.可证得△ABC≌△ADE.四边形AEDF为矩形,设BC为m,则DE=AF=m,DF=AE=AC=4m,∴CF=3m,
F
E
4.已知a≠0,b<0,一次函数是y=ax+b,二次函数是y=
ax2,则下面图中,可以成立的是( )
C
5.填空:已知二次函数
(1)其中开口向上的有_______(填题号);
(2)其中开口向下且开口最大的是____(填题号);
(3)当自变量由小到大变化时,函数值先逐渐变大,然后
逐渐变小的有__________(填题号).
②③⑥
①④⑤
⑤
1.二次函数y=ax2的图象是什么?
2.二次函数y=ax2的图象有什么性质?
3.抛物线y=ax2 与y=-ax2有怎样的关系?
通过本课时的学习,需要我们掌握:
5.4 二次函数的图象和性质
第1课时
1.知道二次函数的图象是抛物线;
2.会画y=ax2的图象,并能结合图象理解y=ax2的性质.
一次函数的图象是一条直线,反比例函数的图象是双曲线,二次函数的图象是什么形状呢?通常怎样画一个函数的图象?
思考
用描点法画二次函数y=x2的图象
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
9
4
1
1
0
4
9
观察y=x2的表达式,选择适当x值,并计算
相应的y值,完成下表:
x
y
0
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
描点
连线
y=x2
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.
这条抛物线关于y轴对称,y轴就是它的对称轴.
对称轴与抛线的交点叫做抛物线的顶点,
顶点是抛物线的最低点或最高点.
y
0
x
...
...
...
...
0
-4
-3
-2
-1
2
3
1
4
0
0.5
2
4.5
8
0.5
2
4.5
8
在同一直角坐标系中,画出y= 的图象.
y
o
2
2
1
x
再画函数 y=2x2 的图象与y=x2的图象相比,有什么共同点和不同点?
y=2x2
y=x2
(1)图象是轴对称图形吗?
如果是,它的对称轴是什么
x
o
图象是轴对称图形,对称轴都是y轴.
图象开口向上, a越大开口越小.
图象的顶点都是原点,为抛物线的最低点.
(2)图象的开口方向是向上还是向下?图象的开口
大小有什么规律?
(3)图象的顶点是什么?顶点是抛物线的最高点还
是最低点?
-3 -2 -1 1 2 3
1
2
x2
=
y
当a>0时,抛物线y=ax2的对称轴是y轴,顶点是原点,开
口向上,顶点是抛物线的最低点,a越大,抛物线的开口越小.
(1)二次函数 y = - x2 的图象是什么形状?
你能根据表格中的数据作出猜想吗?
(2)先想一想,然后作出它的图象.
(3)它与二次函数y=x2的图象有什么关系?
x … -3 -2 -1 0 1 2 3 …
y=-x2
在“做”中“学”
… -9 -4 -1 0 -1 -4 -9 …
x
y
0
-4
-3
-2
1
2
3
4
-4
-2
-1
y=-x2
-1
-3
1
描点,连线
二次函数y= -x2 的图象是抛物线.
二次函数y= -x2 的图象与y= x2 的图象关于x轴对称,顶点都为原点,但原点是二次函数y= -x2的最高点,却是 y= x2 的最低点.
请同学们在同一坐标系内画出y= - 0.5x2,y = -2x2的图象,并考虑这些抛物线有什么共同点和不同点.主要从以下几个方面考虑:
1.开口方向
2.开口大小
3.对称轴
4.顶点坐标
5.有最高点还是有最低点
(1)抛物线y=ax2与y= - ax2(a>0)关于__轴对称;
(2)当a>0时,开口_____,顶点是抛物线的最___点;
当a<0时,开口_____,顶点是抛物线的最___点;
(3)︱a︱越大,抛物线的开口_____.
【点拨】a决定了抛物线y=ax2的开口大小和方向.
x
向上
低
向下
高
越小
【规律总结】
二次函数y=ax2的“两关系四对等”
1.a>0 开口向上 有最小值
2.a<0 开口向下 有最大值
1.物体从某一高度落下,已知下落的高度h(m)和下落的时间t(s)的关系式是:h=4.9t2,h是t的 函数,它的图象的 顶点坐标是 .
2.已知抛物线y=ax2经过点A(-2,-8).
(1)求此抛物线的函数解析式.
(2)判断点B(-1,-4)是否在此抛物线上.
(3)求出此抛物线上纵坐标为-6的点的坐标.
(0,0)
二次
y = -2x2
不在抛物线上
3.如图,在四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
解析:选C.如图,作∠CAE=90°,作DE⊥AE于E,作DF⊥AC于F.可证得△ABC≌△ADE.四边形AEDF为矩形,设BC为m,则DE=AF=m,DF=AE=AC=4m,∴CF=3m,
F
E
4.已知a≠0,b<0,一次函数是y=ax+b,二次函数是y=
ax2,则下面图中,可以成立的是( )
C
5.填空:已知二次函数
(1)其中开口向上的有_______(填题号);
(2)其中开口向下且开口最大的是____(填题号);
(3)当自变量由小到大变化时,函数值先逐渐变大,然后
逐渐变小的有__________(填题号).
②③⑥
①④⑤
⑤
1.二次函数y=ax2的图象是什么?
2.二次函数y=ax2的图象有什么性质?
3.抛物线y=ax2 与y=-ax2有怎样的关系?
通过本课时的学习,需要我们掌握:
