青岛版九年级数学下册 5.2反比例函数 复习教案 (共2份)
文档属性
| 名称 | 青岛版九年级数学下册 5.2反比例函数 复习教案 (共2份) |

|
|
| 格式 | doc | ||
| 文件大小 | 499.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-06 00:00:00 | ||
图片预览



文档简介
反比例函数专题复习
【课标要点】
1.掌握反比例函数的图象及性质;
2.会求反比例函数的解析式;
3.会画反比例函数的图象.
【知识网络】
第1讲 反比例函数
【知识要点】
1、一般地,函数或叫做反比例函数.
2、反比例函数图象的特点:
⑴当时,图象位于一、三象限,在每一象限内,y随x增大而减小.
⑵当时,图象位于二、四象限,在每一象限内,y随x增大而增大.
【典型例题】
例1 已知
⑴如果是的正比例函数,求的值;
⑵如果是的反比例函数,求的值.
分析:根据正比例函数和反比例函数的概念,正比例函数要满足中的指数为1,又要满足系数而反比例函数须满足的指数为-1,且系数
解:⑴若是的正比例函数,由题意知:
解得: 所以
故若是的正比例函数,则
⑵若是的反比例函数,由题意知:
解得: 所以
故若是的反比例函数,则
例2.的反比例函数,下表给出了与的一些值:
x -2 -1 1 3
y 2 -1
⑴写出这个反比例函数的表达式;
⑵根据函数表达式完成上表.
分析:已知是的反比例函数,根据图表中给出的信息求出反比例函数此问题的关键在于确定的值.
解:⑴设反比例函数为当时,得所以反比例函数为.
⑵利用函数表达式把已知的或的值代入表达式,即可解出未知或的值.从左到右依次填:
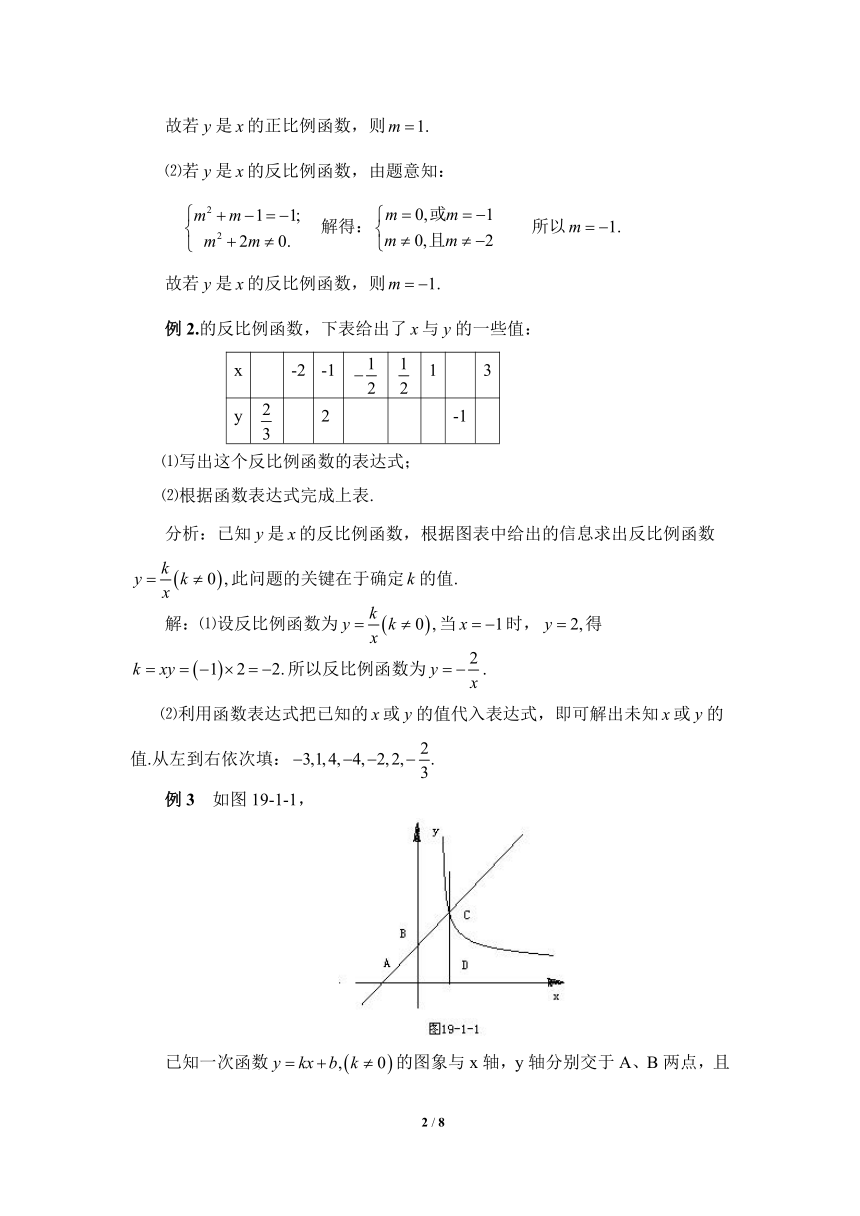
例3 如图19-1-1,
已知一次函数的图象与x轴,y轴分别交于A、B两点,且与反比例函数的图象在第一象限交于C点,CD垂直于x轴,垂足为D,若
⑴求点的坐标;
⑵求一次函数和反比例函数的解析式.
分析:⑴由及点所在的坐标轴的特征,直接写出三点坐标.先由点坐标确定一次函数的解析式,然后求出点坐标,最后确定反比例函数的解析式.
解:⑴∵,∴.
⑵∵在一次函数的图象上,
∴ 解得:
∴一次函数解析式为:
∴C点在一次函数的图象上,且轴. ∴点的坐标为(1,2).
又∵C点在反比例函数的图象上,∴将C(1,2)点代入,得
∴反比例函数的解析式为
【知识运用】
一、解答题
1.已知反比例函数与一次函数的图象都经过点,并且在时,这两个函数的函数值相等,求这两个函数的解析式.
2.如图,已知两点是反比例函数 的图象上任意两点,过两点分别作轴的垂线,垂足分别是,连结 求梯形的面积与的面积是多少?
第2讲 反比例函数的应用
【知识要点】
1.反比例函数的应用就是指运用反比例函数的概念、性质去解决实际问题,因此必须要通过对题目的阅读理解抽象出实际问题的函数关系,再利用反比例函数的思想去解决.
2.应注意以下几个问题:⑴在反比例函数关系中,(定值);⑵在实际问题中:.
【典型例题】
例1一定质量的氧气,它的密度是它的体积的反比例函数,当时,
⑴ 求与的函数关系式;
⑵求当时,氧气的密度.
分析:由题意知:,把、的已知数值代入即可求出常数,再把代入即可求出.
解:⑴设,当时,
∴, ∴
∴与的函数关系是.
⑵当时,,
当时,氧气的密度为
例2 已知:正方形的面积为9,点为坐标原点,点在轴上,点在轴上,点在函数 的图象上,点是函数 的图象上的任意一点,过点分别作轴和轴的垂线,垂足分别为并设矩形不重合的部分的面积为如图19-2-1所示.
⑴求点的坐标和的值;
⑵当时,求点的坐标;
⑶写出与之间的函数关系式.
分析:⑴先根据面积求出点坐标,再根据函数图象过这点求出的值;⑵由于图形不定应当讨论.
解:⑴根据题意得:∴点的坐标为
把代入中,得
⑵∵在函数上,∴
①当时,如图19-2-2所示,由已知得解得:
∴即点的坐标为
②当时,如图19-2-2所示,由已知得解得:
∴即点的坐标为
⑶①如图19-2-3所示,当时,∵点的坐标为,且点在上,
∴由已知得:∴
②如图19-2-4所示,当时,同理可得:∴
【知识运用】
一、解答题
1.已知一次函数的图象与反比例函数的图象相交,其中一个交点的纵坐标为6,求一次函数的图象与轴、轴的交点坐标.
反比例函数家庭作业
一、解答题
1.已知二氧化碳的密度与体积的函数关系式是.
求当时二氧化碳的密度;
请写出二氧化碳的密度随的增大(或减小)而变化的情况.
2.已知一次函数与反比例函数的图象在第一象限内的交点为⑴求得值;⑵求一次函数和反比例函数的解析式.
3.已知反比例函数和一次函数的图象都经过点
⑴求点的坐标及这个一次函数的解析式;
⑵若点和点都在这个一次函数的图象上,试通过计算或利用一次函数的性质,说明大于.
参考答案
第1讲
一、解答题
1.
2.设交于点 ∵
∴=,则=+=+=
:=1:1.
第2讲
一、解答题
1.一次函数与轴的交点为,与轴的交点为
反比例函数家庭作业
一、解答题
1.⑴; ⑵密度随体积的增大而减小.
2. ⑴;⑵
3. ⑴一次函数的解析式为
⑵由一次函数的图象可知.在其定义域内随的增大而减小,
又∵, ∴
1 / 8
【课标要点】
1.掌握反比例函数的图象及性质;
2.会求反比例函数的解析式;
3.会画反比例函数的图象.
【知识网络】
第1讲 反比例函数
【知识要点】
1、一般地,函数或叫做反比例函数.
2、反比例函数图象的特点:
⑴当时,图象位于一、三象限,在每一象限内,y随x增大而减小.
⑵当时,图象位于二、四象限,在每一象限内,y随x增大而增大.
【典型例题】
例1 已知
⑴如果是的正比例函数,求的值;
⑵如果是的反比例函数,求的值.
分析:根据正比例函数和反比例函数的概念,正比例函数要满足中的指数为1,又要满足系数而反比例函数须满足的指数为-1,且系数
解:⑴若是的正比例函数,由题意知:
解得: 所以
故若是的正比例函数,则
⑵若是的反比例函数,由题意知:
解得: 所以
故若是的反比例函数,则
例2.的反比例函数,下表给出了与的一些值:
x -2 -1 1 3
y 2 -1
⑴写出这个反比例函数的表达式;
⑵根据函数表达式完成上表.
分析:已知是的反比例函数,根据图表中给出的信息求出反比例函数此问题的关键在于确定的值.
解:⑴设反比例函数为当时,得所以反比例函数为.
⑵利用函数表达式把已知的或的值代入表达式,即可解出未知或的值.从左到右依次填:
例3 如图19-1-1,
已知一次函数的图象与x轴,y轴分别交于A、B两点,且与反比例函数的图象在第一象限交于C点,CD垂直于x轴,垂足为D,若
⑴求点的坐标;
⑵求一次函数和反比例函数的解析式.
分析:⑴由及点所在的坐标轴的特征,直接写出三点坐标.先由点坐标确定一次函数的解析式,然后求出点坐标,最后确定反比例函数的解析式.
解:⑴∵,∴.
⑵∵在一次函数的图象上,
∴ 解得:
∴一次函数解析式为:
∴C点在一次函数的图象上,且轴. ∴点的坐标为(1,2).
又∵C点在反比例函数的图象上,∴将C(1,2)点代入,得
∴反比例函数的解析式为
【知识运用】
一、解答题
1.已知反比例函数与一次函数的图象都经过点,并且在时,这两个函数的函数值相等,求这两个函数的解析式.
2.如图,已知两点是反比例函数 的图象上任意两点,过两点分别作轴的垂线,垂足分别是,连结 求梯形的面积与的面积是多少?
第2讲 反比例函数的应用
【知识要点】
1.反比例函数的应用就是指运用反比例函数的概念、性质去解决实际问题,因此必须要通过对题目的阅读理解抽象出实际问题的函数关系,再利用反比例函数的思想去解决.
2.应注意以下几个问题:⑴在反比例函数关系中,(定值);⑵在实际问题中:.
【典型例题】
例1一定质量的氧气,它的密度是它的体积的反比例函数,当时,
⑴ 求与的函数关系式;
⑵求当时,氧气的密度.
分析:由题意知:,把、的已知数值代入即可求出常数,再把代入即可求出.
解:⑴设,当时,
∴, ∴
∴与的函数关系是.
⑵当时,,
当时,氧气的密度为
例2 已知:正方形的面积为9,点为坐标原点,点在轴上,点在轴上,点在函数 的图象上,点是函数 的图象上的任意一点,过点分别作轴和轴的垂线,垂足分别为并设矩形不重合的部分的面积为如图19-2-1所示.
⑴求点的坐标和的值;
⑵当时,求点的坐标;
⑶写出与之间的函数关系式.
分析:⑴先根据面积求出点坐标,再根据函数图象过这点求出的值;⑵由于图形不定应当讨论.
解:⑴根据题意得:∴点的坐标为
把代入中,得
⑵∵在函数上,∴
①当时,如图19-2-2所示,由已知得解得:
∴即点的坐标为
②当时,如图19-2-2所示,由已知得解得:
∴即点的坐标为
⑶①如图19-2-3所示,当时,∵点的坐标为,且点在上,
∴由已知得:∴
②如图19-2-4所示,当时,同理可得:∴
【知识运用】
一、解答题
1.已知一次函数的图象与反比例函数的图象相交,其中一个交点的纵坐标为6,求一次函数的图象与轴、轴的交点坐标.
反比例函数家庭作业
一、解答题
1.已知二氧化碳的密度与体积的函数关系式是.
求当时二氧化碳的密度;
请写出二氧化碳的密度随的增大(或减小)而变化的情况.
2.已知一次函数与反比例函数的图象在第一象限内的交点为⑴求得值;⑵求一次函数和反比例函数的解析式.
3.已知反比例函数和一次函数的图象都经过点
⑴求点的坐标及这个一次函数的解析式;
⑵若点和点都在这个一次函数的图象上,试通过计算或利用一次函数的性质,说明大于.
参考答案
第1讲
一、解答题
1.
2.设交于点 ∵
∴=,则=+=+=
:=1:1.
第2讲
一、解答题
1.一次函数与轴的交点为,与轴的交点为
反比例函数家庭作业
一、解答题
1.⑴; ⑵密度随体积的增大而减小.
2. ⑴;⑵
3. ⑴一次函数的解析式为
⑵由一次函数的图象可知.在其定义域内随的增大而减小,
又∵, ∴
1 / 8
