人教版数学八年级下册同步课时训练 19.1.2 函数的图像 两课时(word版含答案)
文档属性
| 名称 | 人教版数学八年级下册同步课时训练 19.1.2 函数的图像 两课时(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 331.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-06 09:12:18 | ||
图片预览


文档简介
19.1.2 第1课时 函数的图象及其画法
1 从函数图象中读取信息
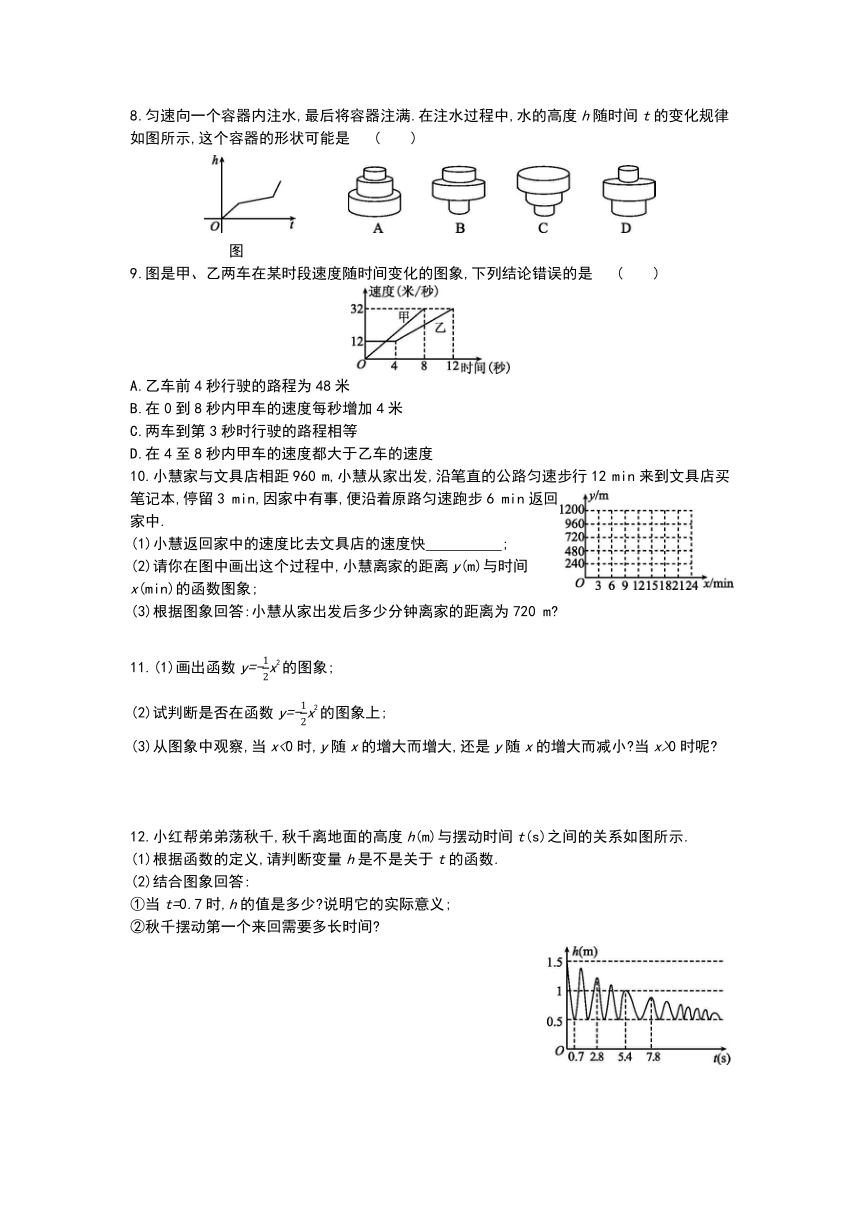
1.如图所示的各图象中,不表示y是x的函数的是 ( )
2.(2020陕西)如图是A市某一天的气温随时间变化的情况图,则这天的日温差(最高气温与最低气温的差)是 ( )
A.4 ℃ B.8 ℃ C.12 ℃ D.16 ℃
图
3.图反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离家的距离.小明家、菜地、玉米地在同一条直线上.
(1)小明从家到菜地用了 分钟,菜地离小明家有 千米;
(2)小明给菜地浇水用了 分钟;
(3)从菜地到玉米地用了 分钟,菜地离玉米地有 千米;
(4)小明给玉米地锄草用了 分钟;
(5)玉米地离小明家有 千米,小明从玉米地回家的平均速度是 千米/分.
2 函数图象上的点与函数解析式的关系
4.下列四点中,在函数y=3x+2的图象上的是 ( )
A.(0,-2) B. C D.
5.(2021赤峰)已知点P(a,b)在函数y=4x+3的图象上,则代数式8a-2b+1的值为 ( )
A.5 B.-5 C.7 D.-6
3 画函数图象
6.(教材练习T1变式)(1)画出函数y=2x-1的图象;
(2)判断点(1,1),(-1,0),(-2,3)是否在函数y=2x-1的图象上;
(3)若点P(m,9)在函数y=2x-1的图象上,求m的值.
7.(2021海南)李叔叔开车上班,最初以某一速度匀速行驶,中途停车加油耽误了几分钟,为了按时到单位,李叔叔在不违反交通规则的前提下加快了速度,仍保持匀速行驶,则汽车行驶的路程y(千米)与行驶的时间t(时)的函数关系的大致图象是 ( )
8.匀速向一个容器内注水,最后将容器注满.在注水过程中,水的高度h随时间t的变化规律如图所示,这个容器的形状可能是 ( )
图
9.图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是 ( )
A.乙车前4秒行驶的路程为48米
B.在0到8秒内甲车的速度每秒增加4米
C.两车到第3秒时行驶的路程相等
D.在4至8秒内甲车的速度都大于乙车的速度
10.小慧家与文具店相距960 m,小慧从家出发,沿笔直的公路匀速步行12 min来到文具店买笔记本,停留3 min,因家中有事,便沿着原路匀速跑步6 min返回家中.
(1)小慧返回家中的速度比去文具店的速度快 ;
(2)请你在图中画出这个过程中,小慧离家的距离y(m)与时间x(min)的函数图象;
(3)根据图象回答:小慧从家出发后多少分钟离家的距离为720 m
11.(1)画出函数y=-x2的图象;
(2)试判断是否在函数y=-x2的图象上;
(3)从图象中观察,当x<0时,y随x的增大而增大,还是y随x的增大而减小 当x>0时呢
12.小红帮弟弟荡秋千,秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图所示.
(1)根据函数的定义,请判断变量h是不是关于t的函数.
(2)结合图象回答:
①当t=0.7时,h的值是多少 说明它的实际意义;
②秋千摆动第一个来回需要多长时间
第2课时 函数的表示方法
1 函数的三种表示方法
1.甲、乙施工队分别从两端修一段长度为380米的公路.在施工过程中,乙队曾因技术改进而停工一天,之后加快了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的.
施工时间/天 1 2 3 4 5 6 7 8 9
累计完成施工量/米 35 70 105 140 160 215 270 325 380
下列说法错误的是 ( )
A.甲队每天修路20米 B.乙队第一天修路15米
C.乙队技术改进后每天修路35米 D.前七天甲、乙两队修路长度相等
2.已知A,B两地相距3千米,小黄从A地到B地,平均速度为4千米/时,若用x(时)表示行走的时间,y(千米)表示余下的路程,则y关于x的函数解析式是 ( )
A.y=4x(x≥0) B.y=4x-3x≥ C.y=3-4x(x≥0) D.y=3-4x0≤x≤
3.(2021青海)新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远地甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用s1,s2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是 ( )
4.如图4,△ABC的边BC的长是8,BC边上的高AD'是4,点D在BC边上运动,设BD的长为x,请写出△ACD的面积y与x之间的函数解析式: .
5.心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间有如下关系(其中2≤x≤20):
提出概念所用的时间x(分) 2 5 7 10 12 13 14 17 20
对概念的接受能力y 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55
(1)上表反映了哪两个变量之间的关系
(2)当提出概念所用时间是10分钟时,学生的接受能力是多少
(3)根据表格中的数据,你认为提出概念所用时间是几分钟时,学生对概念的接受能力最强
(4)从表中可知,当提出概念所用时间x在什么范围内时,学生的接受能力逐步增强 当提出概念所用时间x在什么范围内时,学生的接受能力逐步降低
2 函数三种表示方法的综合应用
6.老师告诉小红:“离地面越高,温度越低.”并给小红出示了下面的表格:
距离地面的高度/km 0 1 2 3 4 5
温度/℃ 20 14 8 2 -4 -10
根据上表,老师还给小红提出了下面几个问题,请你和小红一起来回答:
(1)上表反映了哪两个变量之间的关系 哪个是自变量
(2)如果用h表示距离地面的高度,用t表示温度,请你用含h的式子表示t.
(3)请你利用(2)的结论回答下列问题:
①距离地面6 km的高空的温度是多少
②当高空某处温度为-40 ℃时,求该处的高度.
7.(2021北京海淀区期中)汽车的“燃油效率”是指汽车每消耗1 L汽油最多可行驶的千米数.如图5描述了A,B两辆汽车在不同速度下的燃油效率情况.根据图中信息,下面4个推断中,合理的是 ( )
A.消耗1 L汽油,A车最多可行驶5 km
B.B车以40 km/h的速度行驶1 h,最少消耗4 L汽油
C.对于A车而言,行驶速度越快越省油
D.某城市机动车最高限速为80 km/h,相同条件下,在该市驾驶A车比驾驶B车更省油
8.已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是 ( )
9.用一根长20 cm的细绳围成一个长方形,这个长方形的一边长为x cm,它的面积为y cm2.
(1)写出y与x之间的函数关系式,在这个关系式中,哪个是自变量 自变量的取值范围是怎样的
(2)在下面的表格中填上当x从1变到9时(每次增加1)y的相应值;
边长x(cm) 1 2 3 4 5 6 7 8 9
面积y(cm2)
(3)根据表格中的数据,请你猜想一下,怎样围才能使得到的长方形的面积最大 最大是多少
(4)请你估计一下,当围成的长方形的面积是22 cm2时,x的值应在哪两个相邻整数之间
19.1.2 第1课时 函数的图象及其画法
1.C 2.C
3.(1)15 1.1 (2)10 (3)12 0.9
(4)18 (5)2
4.C 如果点的坐标满足函数解析式,那么这个点就在这个函数的图象上,通过计算,可知选C.
5.B
6.解:(1)列表:
x … -2 -1 0 1 2 3 …
y … -5 -3 -1 1 3 5 …
根据表中数据描点(x,y),并用平滑曲线连接这些点,如图.
(2)当x=1时,y=1;当x=-1时,y=-3≠0;当x=-2时,y=-5≠3.
故点(1,1)在函数y=2x-1的图象上,点(-1,0),(-2,3)不在函数y=2x-1的图象上.
(3)把(m,9)代入y=2x-1,得2m-1=9,解得m=5,所以m的值为5.
7.B 8.D
9.C A项,根据图象可得,乙车前4秒行驶的路程为12×4=48(米),正确;
B项,根据图象可得,在0到8秒内甲车的速度从0米/秒均匀增加到32米/秒,则每秒增加32÷8=4(米),正确;
C项,由B项可知甲车第3秒的速度为12米/秒,而在此之前的速度均小于12米/秒,故甲车从运动开始到第3秒时,行驶的路程小于36米,而乙车在0到3秒内的速度均为12米/秒,所以乙车从运动开始到第3秒时,行驶的路程为36米,所以两车到第3秒时行驶的路程不相等,错误;
D项,在4至8秒内甲车的速度都大于乙车的速度,正确.故选C.
10.解:(1)80 m/min
由题意可得,960÷6-960÷12=80(m/min),
即小慧返回家中的速度比去文具店的速度快80 m/min.
(2)如图所示.
(3)根据图象可得,小慧从家出发后9 min或16.5 min离家的距离为720 m.
11.解:(1)列表如下:
x … -3 -2 -1 0 1 2 3 …
y … -4.5 -2 -0.5 0 -0.5 -2 -4.5 …
根据表中数值描点(x,y),并用平滑曲线连接这些点,如图.
(2)当x=-4时,y=-×(-4)∴不在函数y=-x2的图象上.
(3)当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
12.解:(1)∵对于每一个摆动时间t,都有一个唯一确定的h值与其对应,
∴变量h是关于t的函数.
(2)①当t=0.7时,h=0.5,它的实际意义是秋千摆动0.7 s时,离地面的高度为0.5 m.
②2.8 s.
第2课时 函数的表示方法
1.D 从表格中观察自变量与函数的变化关系,从第1天到第4天可以看出每天的变化量相同,第5天发生了改变,这说明正是乙队停工的那一天,从而推出甲队每天修路20米,故A选项正确;根据两队第一天共修路35米算得乙队第一天修路15米,故B选项正确;通过第6天累计完成的施工量,能算出乙队技术改进后每天修路35米,故C选项正确;因甲队每天修路20米,故前7天甲队一共修了140米,第7天两队累计完成施工量为270米,从而算出乙队前7天一共修了130米,所以前7天甲、乙两队修路长度不相等,故D选项错误.
故选D.
2.D
3.C A项,此函数图象中,s2先达到最大值,即兔子先到终点,不符合题意;
B项,此函数图象中,s2第2段随时间增加其路程一直保持不变,与“当它一觉醒来,发现乌龟已经超过它,于是奋力直追”不符,不符合题意;
C项,此函数图象中,乌龟和兔子同时到达终点,符合题意;
D项,此函数图象中,s1先达到最大值,即乌龟先到终点,不符合题意.
故选C.
4.y=-2x+16 由题意可得,△ACD的面积y与x之间的函数解析式为y=AD'·DC=×4×(8-x)=-2x+16.
5.解:(1)表格反映了提出概念所用的时间x和对概念的接受能力y两个变量之间的关系.
(2)当x=10时,y=59,所以当提出概念所用时间是10分钟时,学生的接受能力是59.
(3)当x=13时,y的值最大,是59.9,所以提出概念所用时间是13分钟时,学生对概念的接受能力最强.
(4)由表中数据可知:当2≤x≤13时,y值逐渐增大,即学生的接受能力逐步增强;当136.解:(1)反映了温度和距离地面的高度之间的关系,距离地面的高度是自变量.
(2)由表可知,高度每上升1 km,温度降低6 ℃,可得t=20-6h.
(3)①当h=6时,t=20-6×6=-16,即距离地面6 km的高空的温度为-16 ℃ .
②将t=-40代入t=20-6h,可得-40=20-6h,解得h=10.
∴当高空某处温度为-40 ℃ 时,该处的高度为10 km.
7.B A项,由图象可知,当A车速度超过40 km/h时,燃油效率大于5 km/L,所以当速度超过40 km/h时,消耗1 L汽油,A车行驶距离大于5 km,故此项不合理,不符合题意;
B项,B车以40 km/h的速度行驶1 h,路程为40 km,40÷10=4(L),故最多消耗4 L汽油,此项合理,符合题意;
C项,对于A车而言,行驶速度在0~80 km/h时,越快越省油,故此项不合理,不符合题意;
D项,某城市机动车最高限速80 km/h,相同条件下,在该市驾驶B车比驾驶A车燃油效率更高,所以更省油,故此项不合理,不符合题意.
故选B.
8.D 由题意,得2x+y=10,
所以y=-2x+10.
由三角形的三边关系,得
解不等式①,得x>2.5,
解不等式②,得x<5,
所以不等式组的解集是2.5故能正确反映y与x之间函数关系的图象是D选项中的图象.故选D.
9.解:(1)y与x之间的函数关系式为y=(20÷2-x)x=(10-x)x=10x-x2.
在这个关系式中,x是自变量,自变量的取值范围为0(2)填表如下:
边长x(cm) 1 2 3 4 5 6 7 8 9
面积y(cm2) 9 16 21 24 25 24 21 16 9
(3)当长方形的长与宽相等,即长、宽均为5 cm时,长方形的面积最大,最大是25 cm2.
(4)由表格可知,当围成的长方形的面积是22 cm2时,x的值应在3~4之间或6~7之间.
1 从函数图象中读取信息
1.如图所示的各图象中,不表示y是x的函数的是 ( )
2.(2020陕西)如图是A市某一天的气温随时间变化的情况图,则这天的日温差(最高气温与最低气温的差)是 ( )
A.4 ℃ B.8 ℃ C.12 ℃ D.16 ℃
图
3.图反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离家的距离.小明家、菜地、玉米地在同一条直线上.
(1)小明从家到菜地用了 分钟,菜地离小明家有 千米;
(2)小明给菜地浇水用了 分钟;
(3)从菜地到玉米地用了 分钟,菜地离玉米地有 千米;
(4)小明给玉米地锄草用了 分钟;
(5)玉米地离小明家有 千米,小明从玉米地回家的平均速度是 千米/分.
2 函数图象上的点与函数解析式的关系
4.下列四点中,在函数y=3x+2的图象上的是 ( )
A.(0,-2) B. C D.
5.(2021赤峰)已知点P(a,b)在函数y=4x+3的图象上,则代数式8a-2b+1的值为 ( )
A.5 B.-5 C.7 D.-6
3 画函数图象
6.(教材练习T1变式)(1)画出函数y=2x-1的图象;
(2)判断点(1,1),(-1,0),(-2,3)是否在函数y=2x-1的图象上;
(3)若点P(m,9)在函数y=2x-1的图象上,求m的值.
7.(2021海南)李叔叔开车上班,最初以某一速度匀速行驶,中途停车加油耽误了几分钟,为了按时到单位,李叔叔在不违反交通规则的前提下加快了速度,仍保持匀速行驶,则汽车行驶的路程y(千米)与行驶的时间t(时)的函数关系的大致图象是 ( )
8.匀速向一个容器内注水,最后将容器注满.在注水过程中,水的高度h随时间t的变化规律如图所示,这个容器的形状可能是 ( )
图
9.图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是 ( )
A.乙车前4秒行驶的路程为48米
B.在0到8秒内甲车的速度每秒增加4米
C.两车到第3秒时行驶的路程相等
D.在4至8秒内甲车的速度都大于乙车的速度
10.小慧家与文具店相距960 m,小慧从家出发,沿笔直的公路匀速步行12 min来到文具店买笔记本,停留3 min,因家中有事,便沿着原路匀速跑步6 min返回家中.
(1)小慧返回家中的速度比去文具店的速度快 ;
(2)请你在图中画出这个过程中,小慧离家的距离y(m)与时间x(min)的函数图象;
(3)根据图象回答:小慧从家出发后多少分钟离家的距离为720 m
11.(1)画出函数y=-x2的图象;
(2)试判断是否在函数y=-x2的图象上;
(3)从图象中观察,当x<0时,y随x的增大而增大,还是y随x的增大而减小 当x>0时呢
12.小红帮弟弟荡秋千,秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图所示.
(1)根据函数的定义,请判断变量h是不是关于t的函数.
(2)结合图象回答:
①当t=0.7时,h的值是多少 说明它的实际意义;
②秋千摆动第一个来回需要多长时间
第2课时 函数的表示方法
1 函数的三种表示方法
1.甲、乙施工队分别从两端修一段长度为380米的公路.在施工过程中,乙队曾因技术改进而停工一天,之后加快了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的.
施工时间/天 1 2 3 4 5 6 7 8 9
累计完成施工量/米 35 70 105 140 160 215 270 325 380
下列说法错误的是 ( )
A.甲队每天修路20米 B.乙队第一天修路15米
C.乙队技术改进后每天修路35米 D.前七天甲、乙两队修路长度相等
2.已知A,B两地相距3千米,小黄从A地到B地,平均速度为4千米/时,若用x(时)表示行走的时间,y(千米)表示余下的路程,则y关于x的函数解析式是 ( )
A.y=4x(x≥0) B.y=4x-3x≥ C.y=3-4x(x≥0) D.y=3-4x0≤x≤
3.(2021青海)新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远地甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用s1,s2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是 ( )
4.如图4,△ABC的边BC的长是8,BC边上的高AD'是4,点D在BC边上运动,设BD的长为x,请写出△ACD的面积y与x之间的函数解析式: .
5.心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间有如下关系(其中2≤x≤20):
提出概念所用的时间x(分) 2 5 7 10 12 13 14 17 20
对概念的接受能力y 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55
(1)上表反映了哪两个变量之间的关系
(2)当提出概念所用时间是10分钟时,学生的接受能力是多少
(3)根据表格中的数据,你认为提出概念所用时间是几分钟时,学生对概念的接受能力最强
(4)从表中可知,当提出概念所用时间x在什么范围内时,学生的接受能力逐步增强 当提出概念所用时间x在什么范围内时,学生的接受能力逐步降低
2 函数三种表示方法的综合应用
6.老师告诉小红:“离地面越高,温度越低.”并给小红出示了下面的表格:
距离地面的高度/km 0 1 2 3 4 5
温度/℃ 20 14 8 2 -4 -10
根据上表,老师还给小红提出了下面几个问题,请你和小红一起来回答:
(1)上表反映了哪两个变量之间的关系 哪个是自变量
(2)如果用h表示距离地面的高度,用t表示温度,请你用含h的式子表示t.
(3)请你利用(2)的结论回答下列问题:
①距离地面6 km的高空的温度是多少
②当高空某处温度为-40 ℃时,求该处的高度.
7.(2021北京海淀区期中)汽车的“燃油效率”是指汽车每消耗1 L汽油最多可行驶的千米数.如图5描述了A,B两辆汽车在不同速度下的燃油效率情况.根据图中信息,下面4个推断中,合理的是 ( )
A.消耗1 L汽油,A车最多可行驶5 km
B.B车以40 km/h的速度行驶1 h,最少消耗4 L汽油
C.对于A车而言,行驶速度越快越省油
D.某城市机动车最高限速为80 km/h,相同条件下,在该市驾驶A车比驾驶B车更省油
8.已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是 ( )
9.用一根长20 cm的细绳围成一个长方形,这个长方形的一边长为x cm,它的面积为y cm2.
(1)写出y与x之间的函数关系式,在这个关系式中,哪个是自变量 自变量的取值范围是怎样的
(2)在下面的表格中填上当x从1变到9时(每次增加1)y的相应值;
边长x(cm) 1 2 3 4 5 6 7 8 9
面积y(cm2)
(3)根据表格中的数据,请你猜想一下,怎样围才能使得到的长方形的面积最大 最大是多少
(4)请你估计一下,当围成的长方形的面积是22 cm2时,x的值应在哪两个相邻整数之间
19.1.2 第1课时 函数的图象及其画法
1.C 2.C
3.(1)15 1.1 (2)10 (3)12 0.9
(4)18 (5)2
4.C 如果点的坐标满足函数解析式,那么这个点就在这个函数的图象上,通过计算,可知选C.
5.B
6.解:(1)列表:
x … -2 -1 0 1 2 3 …
y … -5 -3 -1 1 3 5 …
根据表中数据描点(x,y),并用平滑曲线连接这些点,如图.
(2)当x=1时,y=1;当x=-1时,y=-3≠0;当x=-2时,y=-5≠3.
故点(1,1)在函数y=2x-1的图象上,点(-1,0),(-2,3)不在函数y=2x-1的图象上.
(3)把(m,9)代入y=2x-1,得2m-1=9,解得m=5,所以m的值为5.
7.B 8.D
9.C A项,根据图象可得,乙车前4秒行驶的路程为12×4=48(米),正确;
B项,根据图象可得,在0到8秒内甲车的速度从0米/秒均匀增加到32米/秒,则每秒增加32÷8=4(米),正确;
C项,由B项可知甲车第3秒的速度为12米/秒,而在此之前的速度均小于12米/秒,故甲车从运动开始到第3秒时,行驶的路程小于36米,而乙车在0到3秒内的速度均为12米/秒,所以乙车从运动开始到第3秒时,行驶的路程为36米,所以两车到第3秒时行驶的路程不相等,错误;
D项,在4至8秒内甲车的速度都大于乙车的速度,正确.故选C.
10.解:(1)80 m/min
由题意可得,960÷6-960÷12=80(m/min),
即小慧返回家中的速度比去文具店的速度快80 m/min.
(2)如图所示.
(3)根据图象可得,小慧从家出发后9 min或16.5 min离家的距离为720 m.
11.解:(1)列表如下:
x … -3 -2 -1 0 1 2 3 …
y … -4.5 -2 -0.5 0 -0.5 -2 -4.5 …
根据表中数值描点(x,y),并用平滑曲线连接这些点,如图.
(2)当x=-4时,y=-×(-4)∴不在函数y=-x2的图象上.
(3)当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
12.解:(1)∵对于每一个摆动时间t,都有一个唯一确定的h值与其对应,
∴变量h是关于t的函数.
(2)①当t=0.7时,h=0.5,它的实际意义是秋千摆动0.7 s时,离地面的高度为0.5 m.
②2.8 s.
第2课时 函数的表示方法
1.D 从表格中观察自变量与函数的变化关系,从第1天到第4天可以看出每天的变化量相同,第5天发生了改变,这说明正是乙队停工的那一天,从而推出甲队每天修路20米,故A选项正确;根据两队第一天共修路35米算得乙队第一天修路15米,故B选项正确;通过第6天累计完成的施工量,能算出乙队技术改进后每天修路35米,故C选项正确;因甲队每天修路20米,故前7天甲队一共修了140米,第7天两队累计完成施工量为270米,从而算出乙队前7天一共修了130米,所以前7天甲、乙两队修路长度不相等,故D选项错误.
故选D.
2.D
3.C A项,此函数图象中,s2先达到最大值,即兔子先到终点,不符合题意;
B项,此函数图象中,s2第2段随时间增加其路程一直保持不变,与“当它一觉醒来,发现乌龟已经超过它,于是奋力直追”不符,不符合题意;
C项,此函数图象中,乌龟和兔子同时到达终点,符合题意;
D项,此函数图象中,s1先达到最大值,即乌龟先到终点,不符合题意.
故选C.
4.y=-2x+16 由题意可得,△ACD的面积y与x之间的函数解析式为y=AD'·DC=×4×(8-x)=-2x+16.
5.解:(1)表格反映了提出概念所用的时间x和对概念的接受能力y两个变量之间的关系.
(2)当x=10时,y=59,所以当提出概念所用时间是10分钟时,学生的接受能力是59.
(3)当x=13时,y的值最大,是59.9,所以提出概念所用时间是13分钟时,学生对概念的接受能力最强.
(4)由表中数据可知:当2≤x≤13时,y值逐渐增大,即学生的接受能力逐步增强;当13
(2)由表可知,高度每上升1 km,温度降低6 ℃,可得t=20-6h.
(3)①当h=6时,t=20-6×6=-16,即距离地面6 km的高空的温度为-16 ℃ .
②将t=-40代入t=20-6h,可得-40=20-6h,解得h=10.
∴当高空某处温度为-40 ℃ 时,该处的高度为10 km.
7.B A项,由图象可知,当A车速度超过40 km/h时,燃油效率大于5 km/L,所以当速度超过40 km/h时,消耗1 L汽油,A车行驶距离大于5 km,故此项不合理,不符合题意;
B项,B车以40 km/h的速度行驶1 h,路程为40 km,40÷10=4(L),故最多消耗4 L汽油,此项合理,符合题意;
C项,对于A车而言,行驶速度在0~80 km/h时,越快越省油,故此项不合理,不符合题意;
D项,某城市机动车最高限速80 km/h,相同条件下,在该市驾驶B车比驾驶A车燃油效率更高,所以更省油,故此项不合理,不符合题意.
故选B.
8.D 由题意,得2x+y=10,
所以y=-2x+10.
由三角形的三边关系,得
解不等式①,得x>2.5,
解不等式②,得x<5,
所以不等式组的解集是2.5
9.解:(1)y与x之间的函数关系式为y=(20÷2-x)x=(10-x)x=10x-x2.
在这个关系式中,x是自变量,自变量的取值范围为0
边长x(cm) 1 2 3 4 5 6 7 8 9
面积y(cm2) 9 16 21 24 25 24 21 16 9
(3)当长方形的长与宽相等,即长、宽均为5 cm时,长方形的面积最大,最大是25 cm2.
(4)由表格可知,当围成的长方形的面积是22 cm2时,x的值应在3~4之间或6~7之间.
