2022年强化训练华东师大版七年级数学下册第10章轴对称、平移与旋转单元测试(Word版 含解析 1份打包)
文档属性
| 名称 | 2022年强化训练华东师大版七年级数学下册第10章轴对称、平移与旋转单元测试(Word版 含解析 1份打包) |

|
|
| 格式 | zip | ||
| 文件大小 | 427.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-06 00:00:00 | ||
图片预览

文档简介
七年级数学下册第10章轴对称、平移与旋转单元测试
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2、如图为某小区分类垃圾桶上的标识,其图标部分可以看作轴对称图形的有( )
A.个 B.个 C.个 D.个
3、如图图案中,不是中心对称图形的是( )
A. B. C. D.
4、下列A、B、C、D四幅图案中,能通过平移图案得到的是( )
A. B. C. D.
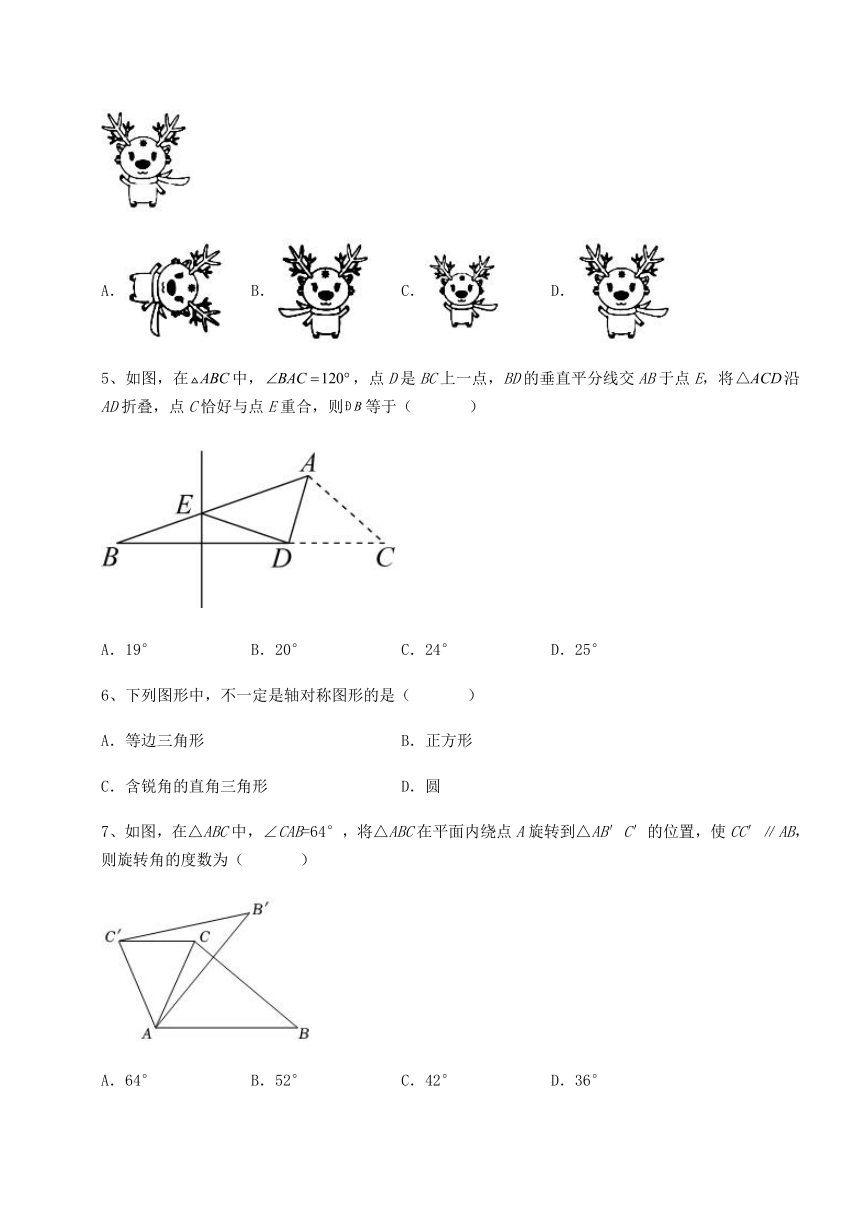
5、如图,在中,,点D是BC上一点,BD的垂直平分线交AB于点E,将沿AD折叠,点C恰好与点E重合,则等于( )
A.19° B.20° C.24° D.25°
6、下列图形中,不一定是轴对称图形的是( )
A.等边三角形 B.正方形
C.含锐角的直角三角形 D.圆
7、如图,在△ABC中,∠CAB=64°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′AB,则旋转角的度数为( )
A.64° B.52° C.42° D.36°
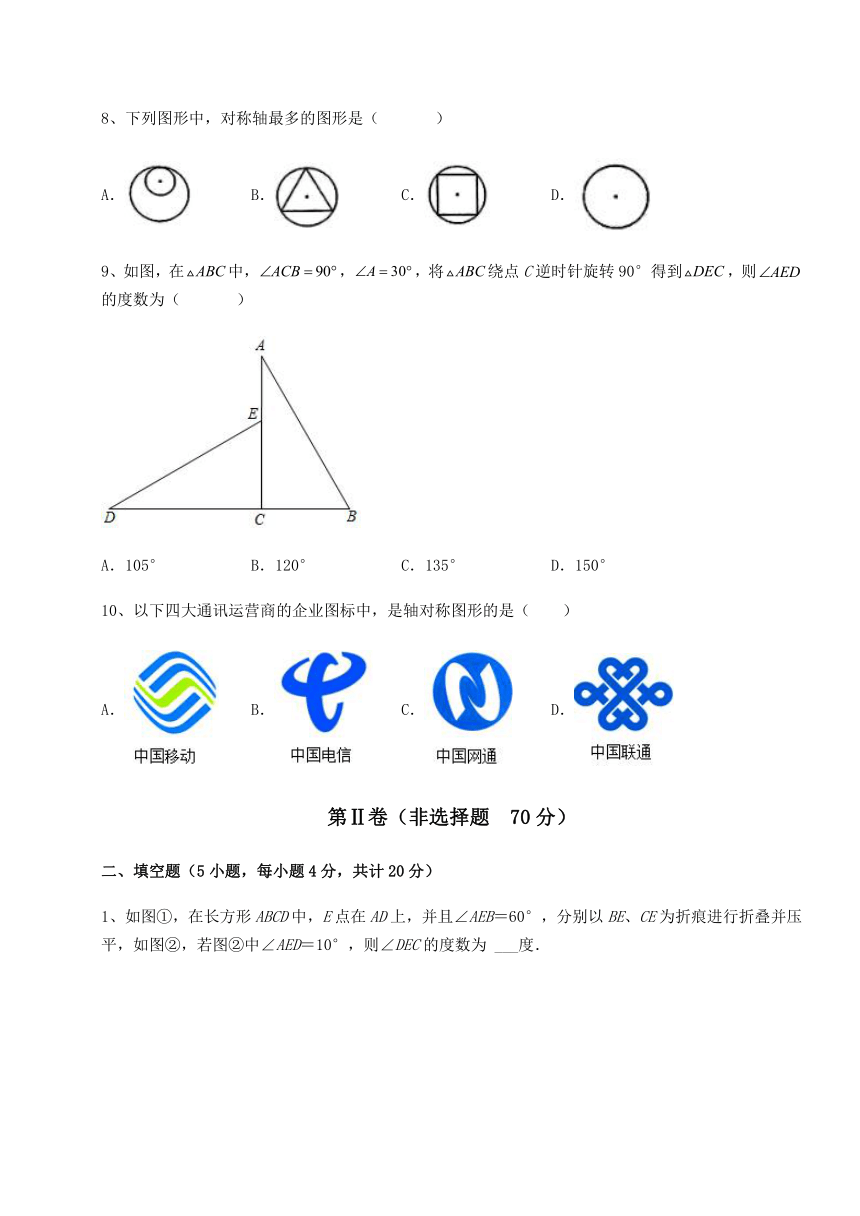
8、下列图形中,对称轴最多的图形是( )
A. B. C. D.
9、如图,在中,,,将绕点C逆时针旋转90°得到,则的度数为( )
A.105° B.120° C.135° D.150°
10、以下四大通讯运营商的企业图标中,是轴对称图形的是( )
A. B. C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
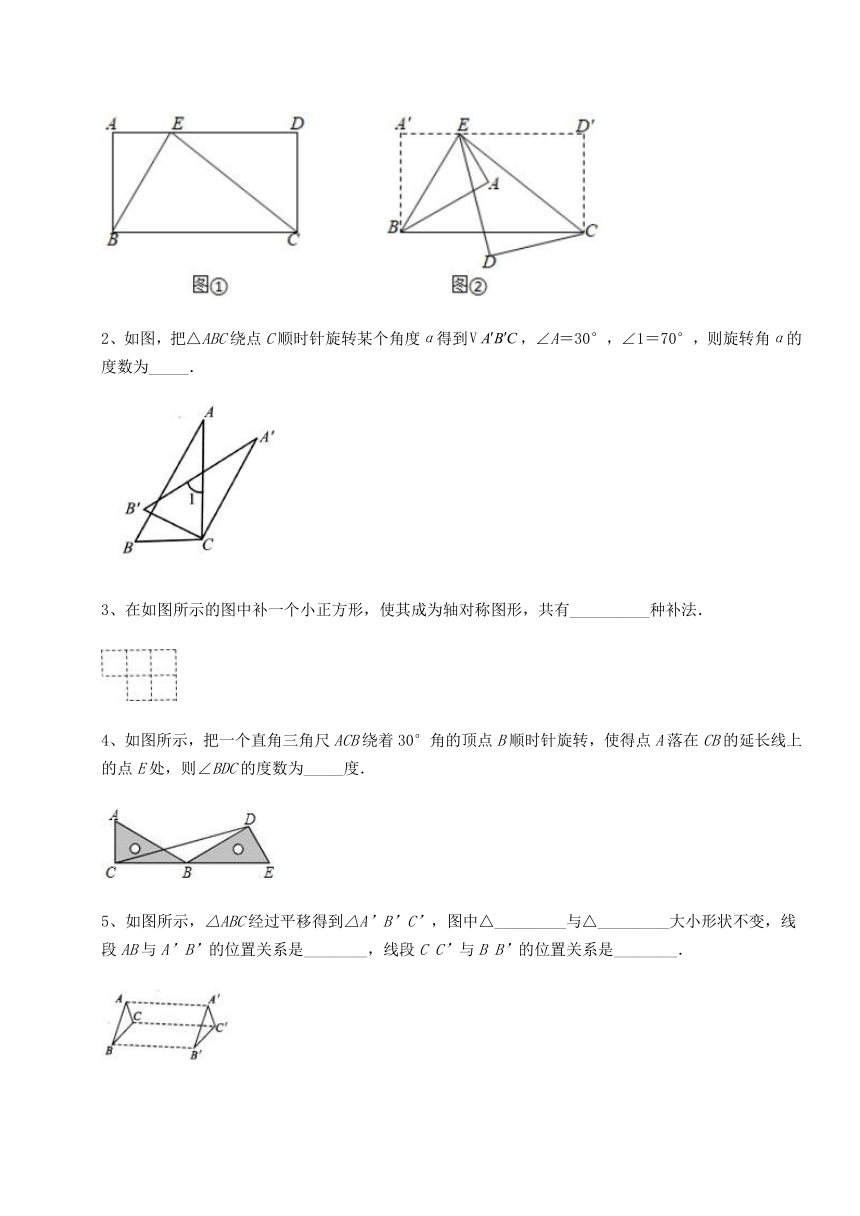
1、如图①,在长方形ABCD中,E点在AD上,并且∠AEB=60°,分别以BE、CE为折痕进行折叠并压平,如图②,若图②中∠AED=10°,则∠DEC的度数为 ___度.
2、如图,把△ABC绕点C顺时针旋转某个角度α得到,∠A=30°,∠1=70°,则旋转角α的度数为_____.
3、在如图所示的图中补一个小正方形,使其成为轴对称图形,共有__________种补法.
4、如图所示,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A落在CB的延长线上的点E处,则∠BDC的度数为_____度.
5、如图所示,△ABC经过平移得到△A’B’C’,图中△_________与△_________大小形状不变,线段AB与A’B’的位置关系是________,线段C C’与B B’的位置关系是________.
三、解答题(5小题,每小题10分,共计50分)
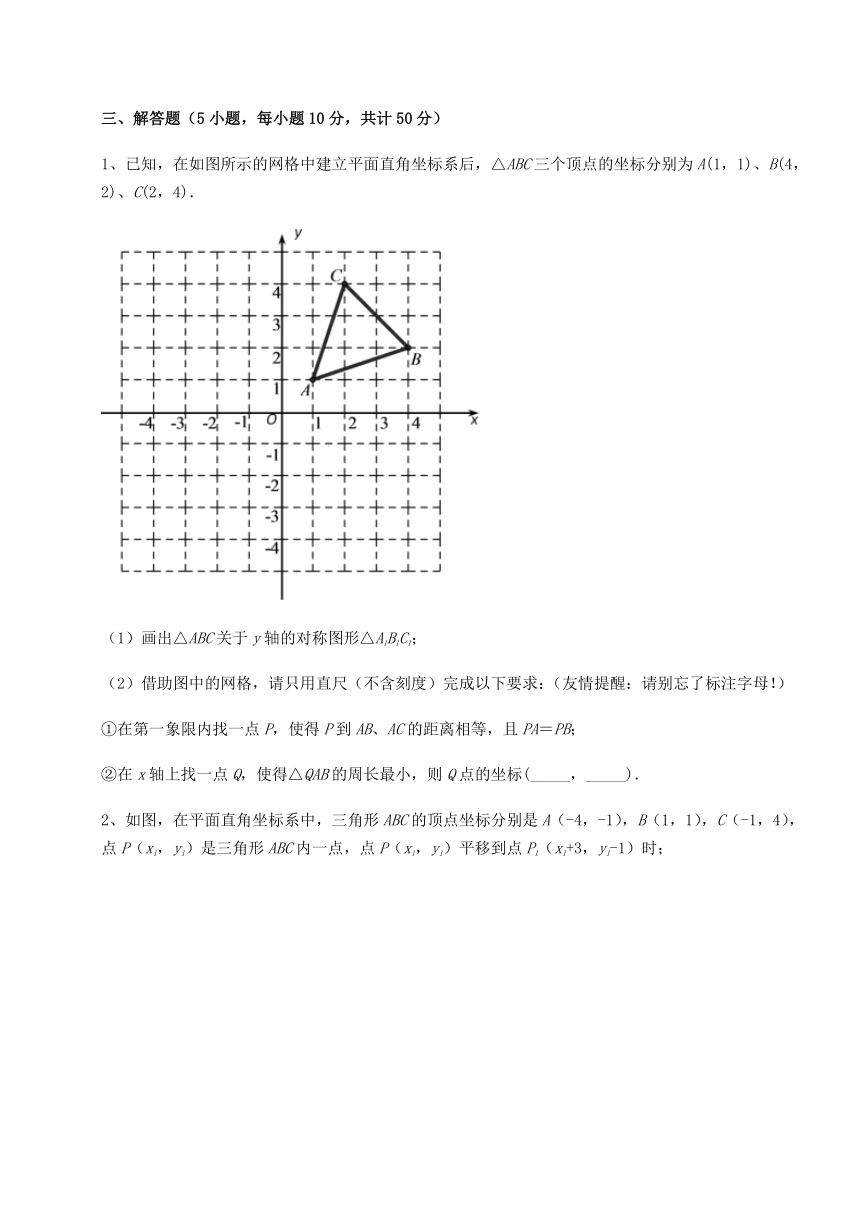
1、已知,在如图所示的网格中建立平面直角坐标系后,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(2,4).
(1)画出△ABC关于y轴的对称图形△A1B1C1;
(2)借助图中的网格,请只用直尺(不含刻度)完成以下要求:(友情提醒:请别忘了标注字母!)
①在第一象限内找一点P,使得P到AB、AC的距离相等,且PA=PB;
②在x轴上找一点Q,使得△QAB的周长最小,则Q点的坐标(_____,_____).
2、如图,在平面直角坐标系中,三角形ABC的顶点坐标分别是A(-4,-1),B(1,1),C(-1,4),点P(x1,y1)是三角形ABC内一点,点P(x1,y1)平移到点P1(x1+3,y1-1)时;
(1)画出平移后的新三角形A1B1C1并分别写出点A1B1C1的坐标;
(2)求出三角形A1B1C1的面积.
3、如图,已知△ABC和直线l,作出△ABC关于直线l的对称图形△A'B'C′.(不写作法,保留作图痕迹)
4、如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方,将图1中的三角板绕点O按顺时针方向旋转一周.
(1)三角板从图1位置旋转到图2位置(OM落在射线OA上),ON旋转的角度为 °;
(2)在三角板从图1旋转到图3位置的过程中,若三角板绕点O按每秒钟15°的速度旋转,当OM所在直线恰好平分∠BOC时,直接写出三角板绕点O运动的时间: 秒;
(3)在旋转过程中,请探究∠BON与∠COM的数量关系.(画出示意图,写出结论,并简要说明理由)
5、如图,将绕点逆时针旋转30°得到,且,两点分别与,两点对应,延长与边交于点,求的度数.
-参考答案-
一、单选题
1、D
【解析】
【详解】
解:.不是轴对称图形,也不是中心对称图形,故本选项不符合题意;
.不是轴对称图形,是中心对称图形,故本选项不符合题意;
.是轴对称图形,不是中心对称图形,故本选项不符合题意;
.既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
【点睛】
本题考查了中心对称图形与轴对称图形的概念,解题的关键是掌握轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
2、B
【解析】
【详解】
解:第一个图形可以看作轴对称图形,符合题意;
第二个图形不可以看作轴对称图形,不符合题意;
第三个图形可以看作轴对称图形,符合题意;
第四个图形不可以看作轴对称图形,不符合题意;
故选:B.
【点睛】
本题考查的是轴对称图形的概念,解题的关键是掌握轴对称图形的对称轴,图形两部分折叠后可重合.
3、C
【解析】
【分析】
根据中心对称图形的概念:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心求解.
【详解】
解:A、是中心对称图形,故A选项不合题意;
B、是中心对称图形,故B选项不合题意;
C、不是中心对称图形,故C选项符合题意;
D、是中心对称图形,故D选项不合题意;
故选:C.
【点睛】
本题考查了中心对称图形的知识,解题的关键是掌握中心对称图形的概念.中心对称图形是要寻找对称中心,旋转180°后重合.
4、D
【解析】
【分析】
根据平移的概念:在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移.
【详解】
解:由平移的性质可知,不改变图形的形状、大小和方向,只有D选项符合要求,
故选:D.
【点睛】
本题考查了生活中的平移现象,图形的平移只改变图形的位置,而不改变图形的形状、大小和方向.
5、B
【解析】
【分析】
根据垂直平分线和等腰三角形性质,得;根据三角形外角性质,得;根据轴对称的性质,得,,;根据补角的性质计算得,根据三角形内角和的性质列一元一次方程并求解,即可得到答案.
【详解】
∵BD的垂直平分线交AB于点E,
∴
∴
∴
∵将沿AD折叠,点C恰好与点E重合,
∴,,
∵
∴
∵
∴
∴
故选:B.
【点睛】
本题考查了轴对称、三角形内角和、三角形外角、补角、一元一次方程的知识;解题的关键是熟练掌握轴对称、三角形内角和、三角形外角的性质,从而完成求解.
6、C
【解析】
【分析】
根据轴对称图形的概念逐一判断即可得.
【详解】
解:A.等边三角形一定是轴对称图形;
B.正方形一定是轴对称图形;
C.含锐角的直角三角形不一定是轴对称图形;
D.圆一定是轴对称图形;
故选:C.
【点睛】
本题主要考查轴对称图形,解题的关键是掌握轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称.
7、B
【解析】
【分析】
先根据平行线的性质得∠ACC′=∠CAB=64°,再根据旋转的性质得∠CAC′等于旋转角,AC=AC′,则利用等腰三角形的性质得∠ACC′=∠AC′C=64°,然后根据三角形内角和定理可计算出∠CAC′的度数,从而得到旋转角的度数.
【详解】
解:∵CC′∥AB,
∴∠ACC′=∠CAB=64°
∵△ABC在平面内绕点A旋转到△AB′C′的位置,
∴∠CAC′等于旋转角,AC=AC′,
∴∠ACC′=∠AC′C=64°,
∴∠CAC′=180°-∠ACC′-∠AC′C=180°-2×64°=52°,
∴旋转角为52°.
故选:B.
【点睛】
本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
8、D
【解析】
【分析】
由对称轴的概念求出图形的对称轴条数即可.
【详解】
A图形有一条对称轴
B图形有三条对称轴
C图形有四条对称轴
D图形有无数条对称轴
故答案为:D.
【点睛】
本题考查了求对称轴条数,其关键是熟悉轴对称图形的概念,如果一个平面图形沿着一条直线折叠,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.这条直线就是它的对称轴.
9、B
【解析】
【分析】
由题意易得,然后根据三角形外角的性质可求解.
【详解】
解:由旋转的性质可得:,
∴;
故选B.
【点睛】
本题主要考查旋转的性质及三角形外角的性质,熟练掌握旋转的性质及三角形外角的性质是解题的关键.
10、D
【解析】
【分析】
根据轴对称图形的定义(在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形)进行判断即可得.
【详解】
解:根据轴对称图形的定义判断可得:只有D选项符合题意,
故选:D.
【点睛】
题目主要考查轴对称图形的判断,理解轴对称图形的定义是解题关键.
二、填空题
1、35
【解析】
【分析】
由折叠可得BE平分,CE平分,再利用角的和差得到=180°-120°+10°=70°,进而可得答案.
【详解】
解:由折叠可得BE平分,CE平分,
∵∠AEB=60°,
∴=2∠AEB=120°,
∵,
∴
∴∠CED=.
故答案为:35.
【点睛】
本题考查角的和差关系,轴对称的性质,根据折叠的性质得到BE平分,CE平分是解本题关键.
2、##度
【解析】
【分析】
由旋转的性质可得再利用三角形的外角的性质求解从而可得答案.
【详解】
解: 把△ABC绕点C顺时针旋转某个角度α得到,∠A=30°,
∠1=70°,
故答案为:
【点睛】
本题考查的是旋转的性质,三角形的外角的性质,利用性质的性质求解是解本题的关键.
3、4
【解析】
【分析】
直接利用轴对称图形的性质得出符合题意的答案.
【详解】
解:如图所示:
故答案为:4
【点睛】
本题考查的是利用轴对称设计图案,熟知轴对称的性质是解答此题的关键.
4、15
【解析】
【分析】
根据旋转的性质△ABC≌△EDB,BC=BD,求出∠CBD的度数,再求∠BDC的度数.
【详解】
解:根据旋转的性质△ABC≌△EDB,BC=BD,
∴△CBD是等腰三角形,
∴∠BDC=∠BCD,
∵∠CBD=180°﹣∠DBE=180°﹣30°=150°,
∴∠BDC=(180°﹣∠CBD)÷2=15°.
故答案为15.
【点睛】
根据旋转的性质,确定各角之间的关系,利用已知条件把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转求出即可.
5、 ABC A’B’C’ 平行 平行
【解析】
【分析】
根据平移的性质:经过平移,对应线段平行且相等,对应角相等,对应点所连接的线段平行且相等,平移不改变图形的形状、大小和方向,进行求解即可.
【详解】
解:∵是△ABC经过平移得到的,
∴图中△ABC与大小形状不变,线段AB与线段的位置关系式平行,线段与线段的关系式平行,
故答案为:ABC,,平行,平行.
【点睛】
本题主要考查了平移的性质,解题的关键在于能够熟练掌握平移的性质.
三、解答题
1、(1)见详解;(2)①见详解;②2,0.
【解析】
【分析】
(1)根据题意画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始,连接这些对称点,就得到原图形的轴对称图形;
(2)①由题意作∠BAC的角平分线,作AB的垂直平分线,交于点P,则点P即为所求;
②由题意作点B关于x轴对称的点B',连接AB',交x轴于Q,则点Q即为所求.根据直线AB'的解析式即可得出点Q的坐标.
【详解】
解:(1)如图所示,△A1B1C1即为所求;
(2)①如图所示,作∠BAC的角平分线,作AB的垂直平分线,交于点P,则点P即为所求;
②如图所示,作点B关于x轴对称的点B',连接AB',交x轴于Q,则点Q即为所求,
∵A(1,1),B'(4,-2),
∴可设直线AB'为y=kx+b,则,
解得:,
∴y=-x+2,
当y=0时,-x+2=0,
解得x=2,
此时点Q的坐标为(2,0).
故答案为:2,0.
【点睛】
本题主要考查利用轴对称进行作图,解决问题的关键是掌握角平分线的性质,中垂线的性质以及待定系数法求一次函数解析式,解题时注意两点之间,线段最短.
2、(1)见解析;A1(-1,-2),B1(4,0),C1(2,3);(2)三角形A1B1C1的面积为.
【解析】
【分析】
(1)分别作出A,B,C的对应点A1,B1,C1即可.
(2)利用分割法求面积即可.
【详解】
(1)∵点平移到点,
∴平移的规律为:向右平移3个单位,向下平移1个单位,
∴为(,),为(4,0),为(2,3);
平移后的三角形如图所示:
(2)面积为:
【点睛】
本题考查作图-复杂作图,三角形的面积,坐标与图形变化-平移等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
3、见解析
【解析】
【分析】
分别作点点点关于直线的对称点,然后连接,,,即可得到△ABC关于直线的轴对称图形△.
【详解】
解:如图:△即为所作:
.
【点睛】
本题考查了轴对称变换,作轴对称图形的依据是轴对称的性质,基本作法是:①先确定图形的关键点;②利用轴对称的性质作出关键点的对称点;③按原图形中的方式顺次连接对称点.
4、(1)90;(2)4或16;(3)见解析,当0°≤α≤30°时,∠BON+∠COM=330°,当30°<α≤180°时,∠COM﹣∠BON=30°,当180°<α≤210°时,∠BON+∠COM=30°,当210°<α≤360°时,∠BON﹣∠COM=30°
【解析】
【分析】
(1)根据旋转的性质知,旋转角∠MON=90°;
(2)分两种情况求解即可;
(3)分四种情况求解即可.
【详解】
解:(1)依题意知,旋转角是∠MON,且∠MON=90°.
故答案为:90;
(2)设运动时间为t秒,
∵∠AOC:∠BOC=2:1,
∴∠AOC=120°,∠BOC=60°,
如图,
当ME平分∠BOC时,
∴∠AOM=∠BOE=BOC=30°,
∴15t=60°,解得t=4.
如图,
当ME平分∠BOC时,
∴∠BOM=BOC=30°,
∴15t=360°﹣120°,解得t=16.
故答案为:4或16;
(3)设旋转角是α,
当0°≤α≤30°时,如图,
∵∠BON=180°﹣α,∠COM=60°+90°+α=150°+α,
∴∠BON+∠COM=330°;
当30°<α≤180°时,如图,
∵∠BON=180°﹣α,∠COM=120°+90°﹣α=210°﹣α,
∴∠COM﹣∠BON=30°;
当180°<α≤210°时,如图,
∵∠BON=α﹣180°,∠COM=120°+90°﹣α=210°﹣α,
∴∠BON+∠COM=30°;
当210°<α≤360°时,如图,
∵∠BON=α﹣180°,∠COM=α﹣210°,
∴∠BON﹣∠COM=30°.
综上,当0°≤α≤30°时,∠BON+∠COM=330°,
当30°<α≤180°时,∠COM﹣∠BON=30°,
当180°<α≤210°时,∠BON+∠COM=30°,
当210°<α≤360°时,∠BON﹣∠COM=30°.
【点睛】
本题考查了旋转的性质,角的和差,以及角平分线的定义等知识,关键是应该认真审题并仔细观察图形,找到各个量之间的关系,数形结合是解题的关键.
5、150°
【解析】
【分析】
由旋转的性质可得,,根据∠ACB+∠ACE=180°,则,.
【详解】
解:由旋转的性质可得,,
∵∠ACB+∠ACE=180°,
∴,
∴.
【点睛】
本题主要考查了旋转的性质,四边形内角和,熟练掌握旋转的性质是解题的关键.
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2、如图为某小区分类垃圾桶上的标识,其图标部分可以看作轴对称图形的有( )
A.个 B.个 C.个 D.个
3、如图图案中,不是中心对称图形的是( )
A. B. C. D.
4、下列A、B、C、D四幅图案中,能通过平移图案得到的是( )
A. B. C. D.
5、如图,在中,,点D是BC上一点,BD的垂直平分线交AB于点E,将沿AD折叠,点C恰好与点E重合,则等于( )
A.19° B.20° C.24° D.25°
6、下列图形中,不一定是轴对称图形的是( )
A.等边三角形 B.正方形
C.含锐角的直角三角形 D.圆
7、如图,在△ABC中,∠CAB=64°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′AB,则旋转角的度数为( )
A.64° B.52° C.42° D.36°
8、下列图形中,对称轴最多的图形是( )
A. B. C. D.
9、如图,在中,,,将绕点C逆时针旋转90°得到,则的度数为( )
A.105° B.120° C.135° D.150°
10、以下四大通讯运营商的企业图标中,是轴对称图形的是( )
A. B. C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、如图①,在长方形ABCD中,E点在AD上,并且∠AEB=60°,分别以BE、CE为折痕进行折叠并压平,如图②,若图②中∠AED=10°,则∠DEC的度数为 ___度.
2、如图,把△ABC绕点C顺时针旋转某个角度α得到,∠A=30°,∠1=70°,则旋转角α的度数为_____.
3、在如图所示的图中补一个小正方形,使其成为轴对称图形,共有__________种补法.
4、如图所示,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A落在CB的延长线上的点E处,则∠BDC的度数为_____度.
5、如图所示,△ABC经过平移得到△A’B’C’,图中△_________与△_________大小形状不变,线段AB与A’B’的位置关系是________,线段C C’与B B’的位置关系是________.
三、解答题(5小题,每小题10分,共计50分)
1、已知,在如图所示的网格中建立平面直角坐标系后,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(2,4).
(1)画出△ABC关于y轴的对称图形△A1B1C1;
(2)借助图中的网格,请只用直尺(不含刻度)完成以下要求:(友情提醒:请别忘了标注字母!)
①在第一象限内找一点P,使得P到AB、AC的距离相等,且PA=PB;
②在x轴上找一点Q,使得△QAB的周长最小,则Q点的坐标(_____,_____).
2、如图,在平面直角坐标系中,三角形ABC的顶点坐标分别是A(-4,-1),B(1,1),C(-1,4),点P(x1,y1)是三角形ABC内一点,点P(x1,y1)平移到点P1(x1+3,y1-1)时;
(1)画出平移后的新三角形A1B1C1并分别写出点A1B1C1的坐标;
(2)求出三角形A1B1C1的面积.
3、如图,已知△ABC和直线l,作出△ABC关于直线l的对称图形△A'B'C′.(不写作法,保留作图痕迹)
4、如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方,将图1中的三角板绕点O按顺时针方向旋转一周.
(1)三角板从图1位置旋转到图2位置(OM落在射线OA上),ON旋转的角度为 °;
(2)在三角板从图1旋转到图3位置的过程中,若三角板绕点O按每秒钟15°的速度旋转,当OM所在直线恰好平分∠BOC时,直接写出三角板绕点O运动的时间: 秒;
(3)在旋转过程中,请探究∠BON与∠COM的数量关系.(画出示意图,写出结论,并简要说明理由)
5、如图,将绕点逆时针旋转30°得到,且,两点分别与,两点对应,延长与边交于点,求的度数.
-参考答案-
一、单选题
1、D
【解析】
【详解】
解:.不是轴对称图形,也不是中心对称图形,故本选项不符合题意;
.不是轴对称图形,是中心对称图形,故本选项不符合题意;
.是轴对称图形,不是中心对称图形,故本选项不符合题意;
.既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
【点睛】
本题考查了中心对称图形与轴对称图形的概念,解题的关键是掌握轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
2、B
【解析】
【详解】
解:第一个图形可以看作轴对称图形,符合题意;
第二个图形不可以看作轴对称图形,不符合题意;
第三个图形可以看作轴对称图形,符合题意;
第四个图形不可以看作轴对称图形,不符合题意;
故选:B.
【点睛】
本题考查的是轴对称图形的概念,解题的关键是掌握轴对称图形的对称轴,图形两部分折叠后可重合.
3、C
【解析】
【分析】
根据中心对称图形的概念:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心求解.
【详解】
解:A、是中心对称图形,故A选项不合题意;
B、是中心对称图形,故B选项不合题意;
C、不是中心对称图形,故C选项符合题意;
D、是中心对称图形,故D选项不合题意;
故选:C.
【点睛】
本题考查了中心对称图形的知识,解题的关键是掌握中心对称图形的概念.中心对称图形是要寻找对称中心,旋转180°后重合.
4、D
【解析】
【分析】
根据平移的概念:在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移.
【详解】
解:由平移的性质可知,不改变图形的形状、大小和方向,只有D选项符合要求,
故选:D.
【点睛】
本题考查了生活中的平移现象,图形的平移只改变图形的位置,而不改变图形的形状、大小和方向.
5、B
【解析】
【分析】
根据垂直平分线和等腰三角形性质,得;根据三角形外角性质,得;根据轴对称的性质,得,,;根据补角的性质计算得,根据三角形内角和的性质列一元一次方程并求解,即可得到答案.
【详解】
∵BD的垂直平分线交AB于点E,
∴
∴
∴
∵将沿AD折叠,点C恰好与点E重合,
∴,,
∵
∴
∵
∴
∴
故选:B.
【点睛】
本题考查了轴对称、三角形内角和、三角形外角、补角、一元一次方程的知识;解题的关键是熟练掌握轴对称、三角形内角和、三角形外角的性质,从而完成求解.
6、C
【解析】
【分析】
根据轴对称图形的概念逐一判断即可得.
【详解】
解:A.等边三角形一定是轴对称图形;
B.正方形一定是轴对称图形;
C.含锐角的直角三角形不一定是轴对称图形;
D.圆一定是轴对称图形;
故选:C.
【点睛】
本题主要考查轴对称图形,解题的关键是掌握轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称.
7、B
【解析】
【分析】
先根据平行线的性质得∠ACC′=∠CAB=64°,再根据旋转的性质得∠CAC′等于旋转角,AC=AC′,则利用等腰三角形的性质得∠ACC′=∠AC′C=64°,然后根据三角形内角和定理可计算出∠CAC′的度数,从而得到旋转角的度数.
【详解】
解:∵CC′∥AB,
∴∠ACC′=∠CAB=64°
∵△ABC在平面内绕点A旋转到△AB′C′的位置,
∴∠CAC′等于旋转角,AC=AC′,
∴∠ACC′=∠AC′C=64°,
∴∠CAC′=180°-∠ACC′-∠AC′C=180°-2×64°=52°,
∴旋转角为52°.
故选:B.
【点睛】
本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
8、D
【解析】
【分析】
由对称轴的概念求出图形的对称轴条数即可.
【详解】
A图形有一条对称轴
B图形有三条对称轴
C图形有四条对称轴
D图形有无数条对称轴
故答案为:D.
【点睛】
本题考查了求对称轴条数,其关键是熟悉轴对称图形的概念,如果一个平面图形沿着一条直线折叠,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.这条直线就是它的对称轴.
9、B
【解析】
【分析】
由题意易得,然后根据三角形外角的性质可求解.
【详解】
解:由旋转的性质可得:,
∴;
故选B.
【点睛】
本题主要考查旋转的性质及三角形外角的性质,熟练掌握旋转的性质及三角形外角的性质是解题的关键.
10、D
【解析】
【分析】
根据轴对称图形的定义(在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形)进行判断即可得.
【详解】
解:根据轴对称图形的定义判断可得:只有D选项符合题意,
故选:D.
【点睛】
题目主要考查轴对称图形的判断,理解轴对称图形的定义是解题关键.
二、填空题
1、35
【解析】
【分析】
由折叠可得BE平分,CE平分,再利用角的和差得到=180°-120°+10°=70°,进而可得答案.
【详解】
解:由折叠可得BE平分,CE平分,
∵∠AEB=60°,
∴=2∠AEB=120°,
∵,
∴
∴∠CED=.
故答案为:35.
【点睛】
本题考查角的和差关系,轴对称的性质,根据折叠的性质得到BE平分,CE平分是解本题关键.
2、##度
【解析】
【分析】
由旋转的性质可得再利用三角形的外角的性质求解从而可得答案.
【详解】
解: 把△ABC绕点C顺时针旋转某个角度α得到,∠A=30°,
∠1=70°,
故答案为:
【点睛】
本题考查的是旋转的性质,三角形的外角的性质,利用性质的性质求解是解本题的关键.
3、4
【解析】
【分析】
直接利用轴对称图形的性质得出符合题意的答案.
【详解】
解:如图所示:
故答案为:4
【点睛】
本题考查的是利用轴对称设计图案,熟知轴对称的性质是解答此题的关键.
4、15
【解析】
【分析】
根据旋转的性质△ABC≌△EDB,BC=BD,求出∠CBD的度数,再求∠BDC的度数.
【详解】
解:根据旋转的性质△ABC≌△EDB,BC=BD,
∴△CBD是等腰三角形,
∴∠BDC=∠BCD,
∵∠CBD=180°﹣∠DBE=180°﹣30°=150°,
∴∠BDC=(180°﹣∠CBD)÷2=15°.
故答案为15.
【点睛】
根据旋转的性质,确定各角之间的关系,利用已知条件把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转求出即可.
5、 ABC A’B’C’ 平行 平行
【解析】
【分析】
根据平移的性质:经过平移,对应线段平行且相等,对应角相等,对应点所连接的线段平行且相等,平移不改变图形的形状、大小和方向,进行求解即可.
【详解】
解:∵是△ABC经过平移得到的,
∴图中△ABC与大小形状不变,线段AB与线段的位置关系式平行,线段与线段的关系式平行,
故答案为:ABC,,平行,平行.
【点睛】
本题主要考查了平移的性质,解题的关键在于能够熟练掌握平移的性质.
三、解答题
1、(1)见详解;(2)①见详解;②2,0.
【解析】
【分析】
(1)根据题意画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始,连接这些对称点,就得到原图形的轴对称图形;
(2)①由题意作∠BAC的角平分线,作AB的垂直平分线,交于点P,则点P即为所求;
②由题意作点B关于x轴对称的点B',连接AB',交x轴于Q,则点Q即为所求.根据直线AB'的解析式即可得出点Q的坐标.
【详解】
解:(1)如图所示,△A1B1C1即为所求;
(2)①如图所示,作∠BAC的角平分线,作AB的垂直平分线,交于点P,则点P即为所求;
②如图所示,作点B关于x轴对称的点B',连接AB',交x轴于Q,则点Q即为所求,
∵A(1,1),B'(4,-2),
∴可设直线AB'为y=kx+b,则,
解得:,
∴y=-x+2,
当y=0时,-x+2=0,
解得x=2,
此时点Q的坐标为(2,0).
故答案为:2,0.
【点睛】
本题主要考查利用轴对称进行作图,解决问题的关键是掌握角平分线的性质,中垂线的性质以及待定系数法求一次函数解析式,解题时注意两点之间,线段最短.
2、(1)见解析;A1(-1,-2),B1(4,0),C1(2,3);(2)三角形A1B1C1的面积为.
【解析】
【分析】
(1)分别作出A,B,C的对应点A1,B1,C1即可.
(2)利用分割法求面积即可.
【详解】
(1)∵点平移到点,
∴平移的规律为:向右平移3个单位,向下平移1个单位,
∴为(,),为(4,0),为(2,3);
平移后的三角形如图所示:
(2)面积为:
【点睛】
本题考查作图-复杂作图,三角形的面积,坐标与图形变化-平移等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
3、见解析
【解析】
【分析】
分别作点点点关于直线的对称点,然后连接,,,即可得到△ABC关于直线的轴对称图形△.
【详解】
解:如图:△即为所作:
.
【点睛】
本题考查了轴对称变换,作轴对称图形的依据是轴对称的性质,基本作法是:①先确定图形的关键点;②利用轴对称的性质作出关键点的对称点;③按原图形中的方式顺次连接对称点.
4、(1)90;(2)4或16;(3)见解析,当0°≤α≤30°时,∠BON+∠COM=330°,当30°<α≤180°时,∠COM﹣∠BON=30°,当180°<α≤210°时,∠BON+∠COM=30°,当210°<α≤360°时,∠BON﹣∠COM=30°
【解析】
【分析】
(1)根据旋转的性质知,旋转角∠MON=90°;
(2)分两种情况求解即可;
(3)分四种情况求解即可.
【详解】
解:(1)依题意知,旋转角是∠MON,且∠MON=90°.
故答案为:90;
(2)设运动时间为t秒,
∵∠AOC:∠BOC=2:1,
∴∠AOC=120°,∠BOC=60°,
如图,
当ME平分∠BOC时,
∴∠AOM=∠BOE=BOC=30°,
∴15t=60°,解得t=4.
如图,
当ME平分∠BOC时,
∴∠BOM=BOC=30°,
∴15t=360°﹣120°,解得t=16.
故答案为:4或16;
(3)设旋转角是α,
当0°≤α≤30°时,如图,
∵∠BON=180°﹣α,∠COM=60°+90°+α=150°+α,
∴∠BON+∠COM=330°;
当30°<α≤180°时,如图,
∵∠BON=180°﹣α,∠COM=120°+90°﹣α=210°﹣α,
∴∠COM﹣∠BON=30°;
当180°<α≤210°时,如图,
∵∠BON=α﹣180°,∠COM=120°+90°﹣α=210°﹣α,
∴∠BON+∠COM=30°;
当210°<α≤360°时,如图,
∵∠BON=α﹣180°,∠COM=α﹣210°,
∴∠BON﹣∠COM=30°.
综上,当0°≤α≤30°时,∠BON+∠COM=330°,
当30°<α≤180°时,∠COM﹣∠BON=30°,
当180°<α≤210°时,∠BON+∠COM=30°,
当210°<α≤360°时,∠BON﹣∠COM=30°.
【点睛】
本题考查了旋转的性质,角的和差,以及角平分线的定义等知识,关键是应该认真审题并仔细观察图形,找到各个量之间的关系,数形结合是解题的关键.
5、150°
【解析】
【分析】
由旋转的性质可得,,根据∠ACB+∠ACE=180°,则,.
【详解】
解:由旋转的性质可得,,
∵∠ACB+∠ACE=180°,
∴,
∴.
【点睛】
本题主要考查了旋转的性质,四边形内角和,熟练掌握旋转的性质是解题的关键.
