华师大版九年级数学下册试题 一课一练27.2.2 直线与圆的位置关系 习题 (word版含答案)
文档属性
| 名称 | 华师大版九年级数学下册试题 一课一练27.2.2 直线与圆的位置关系 习题 (word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 174.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-06 09:57:35 | ||
图片预览





文档简介
27.2.2《直线与圆的位置关系》习题1
第一课时
一、填空题:
1.在Rt△ABC中,∠C=90°,AC=12cm,BC=5cm,以点C为圆心,6cm 的长为半径的圆与直线AB的位置关系是________.
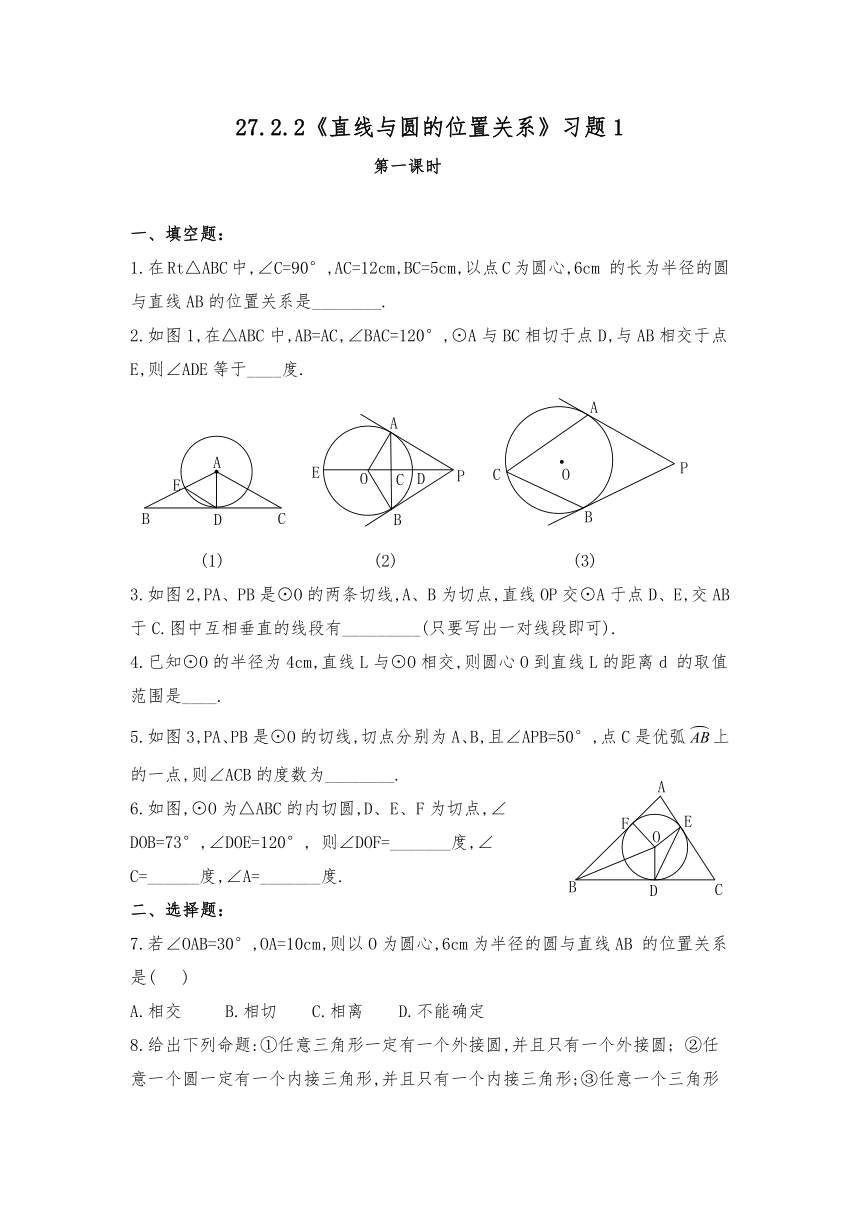
2.如图1,在△ABC中,AB=AC,∠BAC=120°,⊙A与BC相切于点D,与AB相交于点E,则∠ADE等于____度.
(1) (2) (3)
3.如图2,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙A于点D、E,交AB 于C.图中互相垂直的线段有_________(只要写出一对线段即可).
4.已知⊙O的半径为4cm,直线L与⊙O相交,则圆心O到直线L的距离d 的取值范围是____.
5.如图3,PA、PB是⊙O的切线,切点分别为A、B,且∠APB=50°,点C是优弧上的一点,则∠ACB的度数为________.
6.如图,⊙O为△ABC的内切圆,D、E、F为切点,∠DOB=73°,∠DOE=120°, 则∠DOF=_______度,∠C=______度,∠A=_______度.
二、选择题:
7.若∠OAB=30°,OA=10cm,则以O为圆心,6cm为半径的圆与直线AB 的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
8.给出下列命题:①任意三角形一定有一个外接圆,并且只有一个外接圆; ②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;③任意一个三角形一定有一个内切圆,并且只有一个内切圆;④任意一个圆一定有一个外切三角形, 并且只有一个外切三角形,其中真命题共有( )
A.1个 B.2个 C.3个 D.4个
9.如L是⊙O的切线,要判定AB⊥L,还需要添加的条件是( )
A.AB经过圆心O B.AB是直径
C.AB是直径,B是切点 D.AB是直线,B是切点
10.设⊙O的直径为m,直线L与⊙O相离,点O到直线L的距离为d,则d与m的关系是( )
A.d=m B.d>m C.d> D.d<
11.在平面直角坐标系中,以点(-1,2)为圆心,1为半径的圆必与( )
A.x轴相交 B.y轴相交 C.x轴相切 D.y轴相切
12.如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO等于( )
A. 70° B.64° C.62° D.51°
三、解答题:
13.如图,AB是半圆O的直径,C为半圆上一点,过C作半圆的切线,连接AC, 作直线AD,使∠DAC=∠CAB,AD交半圆于E,交过C点的切线于点D.
(1)试判断AD与CD有何位置关系,并说明理由;
(2)若AB=10,AD=8,求AC的长.
14.如图,BC是半圆O的直径,P是BC延长线上一点,PA切⊙O于点A,∠B=30°.
(1)试问AB与AP是否相等 请说明理由.
(2)若PA=,求半圆O的直径.
15.如图,∠PAQ是直角,半径为5的⊙O与AP相切于点T,与AQ相交于两点B、C.
(1)BT是否平分∠OBA 证明你的结论.
(2)若已知AT=4,试求AB的长.
16.如图,有三边分别为0.4m、0.5m和0.6m的三角形形状的铝皮,问怎样剪出一个面积最大的圆形铝皮 请你设计解决问题的方法.
17.如图,AB为半圆O的直径,在AB的同侧作AC、BD切半圆O于A、B,CD切半圆O 于E,请分别写出两个角相等、两条边相等、两个三角形全等、 两个三角形相似等四个正确的结论.
18.如图,已知:⊙D交y轴于A、B,交x轴于C,过点C的直线:y=-2-8 与y轴交于点P.
(1)试判断PC与⊙D的位置关系.
(2)判断在直线PC上是否存在点E,使得S△EOP=4S△CDO,若存在,求出点E的坐标;若不存在,请说明理由.
第二课时
一、选择题:
1.若∠OAB=30°,OA=10cm,则以O为圆心,6cm为半径的圆与射线AB的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
2.Rt△ABC中,∠C=90°,AB=10,AC=6,以C为圆心作⊙C和AB相切,则⊙C的半径长为( )
A.8 B.4 C.9.6 D.4.8
3.⊙O内最长弦长为,直线与⊙O相离,设点O到的距离为,则与的关系是( )
A.= B.> C.> D.<
4.以三角形的一边长为直径的圆切三角形的另一边,则该三角形为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形
5.菱形对角线的交点为O,以O为圆心,以O到菱形一边的距离为半径的圆与其他几边的关系为( )
A.相交 B.相切 C.相离 D.不能确定
6.⊙O的半径为6,⊙O的一条弦AB为6,以3为半径的同心圆与直线AB的位置关系是( )
A.相离 B.相交 C.相切 D.不能确定
7.下列四边形中一定有内切圆的是( )
A.直角梯形 B.等腰梯形 C.矩形 D.菱形
8.已知△ABC的内切圆O与各边相切于D、E、F,那么点O是△DEF的( )
A.三条中线交点 B.三条高的交点
C.三条角平分线交点 D.三条边的垂直平分线的交点
9.给出下列命题:
①任一个三角形一定有一个外接圆,并且只有一个外接圆;
②任一个圆一定有一个内接三角形,并且只有一个内接三角形;
③任一个三角形一定有一个内切圆,并且只有一个内切圆;
④任一个圆一定有一个外切三角形,并且只有一个外切三角形.
其中真命题共有( )
A.1个 B.2个 C.3个 D.4个
二、证明题
1.如图,已知⊙O中,AB是直径,过B点作⊙O的切线BC,连结CO.若AD∥OC交⊙O于D.求证:CD是⊙O的切线.
2.已知:如图,同心圆O,大圆的弦AB=CD,且AB是小圆的切线,切点为E.求证:CD是小圆的切线.
3.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,⊙O的半径为3.
(1)当圆心O与C重合时,⊙O与AB的位置关系怎样?
(2)若点O沿CA移动时,当OC为多少时?⊙C与AB相切?
4.如图,直角梯形ABCD中,∠A=∠B=90°,AD∥BC,E为AB上一点,DE平分∠ADC,CE平分∠BCD,以AB为直径的圆与边CD有怎样的位置关系?
5.有一块锐角三角形木板,现在要用它截成一个最大面积的圆形木板,问怎样才能使圆形木板面积最大?
6.如图,AB是⊙O直径,⊙O过AC的中点D,DE⊥BC,垂足为E.
(1)由这些条件,你能得出哪些结论?(要求:不准标其他字母,找结论过程中所连的辅助线不能出现在结论中,不写推理过程,写出4个结论即可)
(2)若∠ABC为直角,其他条件不变,除上述结论外你还能推出哪些新的正确结论?并画出图形.(要求:写出6个结论即可,其他要求同(1))
7.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.若以C为圆心,R为半径所作的圆与斜边AB只有一个公共点,则R的取值范围是多少?
8.如图,有一块锐角三角形木板,现在要把它截成半圆形板块(圆心在BC上),问怎样截取才能使截出的半圆形面积最大?(要求说明理由)
9.如图,直线ι1、ι2、ι3表示相互交叉的公路.现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有几处?
第一课时参考答案
1.相交 2.60 3.如OA⊥PA,OB⊥PB,AB⊥OP等. 4.0≤d<4. 5.65°
6. 146°,60°,86° 7.A 8.B 9.C 10.C 11.D 12.B
13.(1)AD⊥CD.理由:连接OC,则OC⊥CD.
∵OA=OC,∴∠OAC=∠OCA,
又∠OAC= ∠DAC,∴∠DAC=∠OCA,∴AD∥OC,∴AD⊥CD.
(2)连接BC,则∠ACB=90°由(1)得∠ADC=∠ACB,
又∠DAC=∠CAB.∴△ACD∽△ABC,
∴,即AC2=AD·AB=80,故AC=.
14.(1)相等.理由:连接OA,则∠PAO=90°.
∵OA=OB,∴∠OAB=∠B=30°, ∴∠AOP=60°,∠P=90°-60°=30°,
∴∠P=∠B,∴AB=AP,
(2)∵tan∠APO=,
∴OA=PA, tan∠APO=,
∴BC=2OA=2,即半圆O的直径为2.
15.(1)平分.证明:连接OT,∵PT切⊙O于T,
∴OT⊥PT,故∠OTA=90°,
从而∠OBT=∠OTB=90°-∠ATB=∠ABT.即BT平分∠OBA.
(2)过O作OM⊥BC于M,则四边形OTAM是矩形,
故OM=AT=4,AM=OT=5.在Rt△OBM中, OB=5,OM=4,
故BM==3,从而AB=AM-BM=5-3=2.
16.作出△ABC的内切圆⊙O,沿⊙O的圆周剪出一个圆,其面积最大.
17.由已知得:OA=OE,∠OAC=∠OEC,又OC公共,故△OAC≌OEC,
同理,△OBD ≌△OED,由此可得∠AOC=∠EOC,∠BOD=∠EOD,
从而∠COD=90°,∠AOC=∠BDO.
根据这些写如下结论:
①角相等:∠AOC=∠COE=∠BDO=∠EDO,∠ACO=∠ECO=∠DOE=∠DOB,
∠A=∠B=∠OEC=∠OED,
②边相等:AC=CE,DE=DB,OA=OB=OE;
③全等三角形:△OAC≌△OEC,△OBD≌△OED;
④相似三角形:△AOC∽△EOC∽△EDO∽△BDO∽△ODC.
18. (1)PC与⊙D相切,理由:令x=0,得y=-8,故P(0,-8);令y=0,得x=-2,
故C(-2,0),故OP=8,OC=2,CD=1,
∴CD==3,
又PC=,
∴PC2+CD2=9+72=81=PD2.
从而∠PCD=90°,故PC与⊙D相切.
(2)存在.点E(,-12)或(-,-4),使S△EOP=4S△CDO.
设E点坐标为(x,y),过E作EF⊥y轴于F,则EF=│x│.
∴S△POE=PO·EF=4│x│.
∵S△CDO=CO·DO=.
∴4│x│=4,│x│=,x=±,
当x=- 时,y=-2×(-)-8=-4 ;
当x= 时,y=-2×-8=-12 .
故E点坐标为(-,-4)或(,-12).
第二课时参考答案
一、1-5 A D C B B ; 6-9 C D D B
二、1.提示:连结OC,证△AOC与△BOC全等
2.作垂直证半径,弦心距相等
3.①垂直三角形的高,用面积方法求;②△AOE∽△ABC即可
4.用角平分线定理证明EF=EA=EB即可
5.做三角形的内切圆
6.①DE与⊙O相切,AB=BC,DE2+CE2=CD2,∠C+∠CDE=90°
②BC是⊙O的切线,有DE=1/2AB等.
7.R=2.4或38.∠A角平分线与BC的交点为圆心O,O到AC的距离为半径做圆
9.4
第一课时
一、填空题:
1.在Rt△ABC中,∠C=90°,AC=12cm,BC=5cm,以点C为圆心,6cm 的长为半径的圆与直线AB的位置关系是________.
2.如图1,在△ABC中,AB=AC,∠BAC=120°,⊙A与BC相切于点D,与AB相交于点E,则∠ADE等于____度.
(1) (2) (3)
3.如图2,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙A于点D、E,交AB 于C.图中互相垂直的线段有_________(只要写出一对线段即可).
4.已知⊙O的半径为4cm,直线L与⊙O相交,则圆心O到直线L的距离d 的取值范围是____.
5.如图3,PA、PB是⊙O的切线,切点分别为A、B,且∠APB=50°,点C是优弧上的一点,则∠ACB的度数为________.
6.如图,⊙O为△ABC的内切圆,D、E、F为切点,∠DOB=73°,∠DOE=120°, 则∠DOF=_______度,∠C=______度,∠A=_______度.
二、选择题:
7.若∠OAB=30°,OA=10cm,则以O为圆心,6cm为半径的圆与直线AB 的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
8.给出下列命题:①任意三角形一定有一个外接圆,并且只有一个外接圆; ②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;③任意一个三角形一定有一个内切圆,并且只有一个内切圆;④任意一个圆一定有一个外切三角形, 并且只有一个外切三角形,其中真命题共有( )
A.1个 B.2个 C.3个 D.4个
9.如L是⊙O的切线,要判定AB⊥L,还需要添加的条件是( )
A.AB经过圆心O B.AB是直径
C.AB是直径,B是切点 D.AB是直线,B是切点
10.设⊙O的直径为m,直线L与⊙O相离,点O到直线L的距离为d,则d与m的关系是( )
A.d=m B.d>m C.d> D.d<
11.在平面直角坐标系中,以点(-1,2)为圆心,1为半径的圆必与( )
A.x轴相交 B.y轴相交 C.x轴相切 D.y轴相切
12.如图,AB、AC为⊙O的切线,B、C是切点,延长OB到D,使BD=OB,连接AD,如果∠DAC=78°,那么∠ADO等于( )
A. 70° B.64° C.62° D.51°
三、解答题:
13.如图,AB是半圆O的直径,C为半圆上一点,过C作半圆的切线,连接AC, 作直线AD,使∠DAC=∠CAB,AD交半圆于E,交过C点的切线于点D.
(1)试判断AD与CD有何位置关系,并说明理由;
(2)若AB=10,AD=8,求AC的长.
14.如图,BC是半圆O的直径,P是BC延长线上一点,PA切⊙O于点A,∠B=30°.
(1)试问AB与AP是否相等 请说明理由.
(2)若PA=,求半圆O的直径.
15.如图,∠PAQ是直角,半径为5的⊙O与AP相切于点T,与AQ相交于两点B、C.
(1)BT是否平分∠OBA 证明你的结论.
(2)若已知AT=4,试求AB的长.
16.如图,有三边分别为0.4m、0.5m和0.6m的三角形形状的铝皮,问怎样剪出一个面积最大的圆形铝皮 请你设计解决问题的方法.
17.如图,AB为半圆O的直径,在AB的同侧作AC、BD切半圆O于A、B,CD切半圆O 于E,请分别写出两个角相等、两条边相等、两个三角形全等、 两个三角形相似等四个正确的结论.
18.如图,已知:⊙D交y轴于A、B,交x轴于C,过点C的直线:y=-2-8 与y轴交于点P.
(1)试判断PC与⊙D的位置关系.
(2)判断在直线PC上是否存在点E,使得S△EOP=4S△CDO,若存在,求出点E的坐标;若不存在,请说明理由.
第二课时
一、选择题:
1.若∠OAB=30°,OA=10cm,则以O为圆心,6cm为半径的圆与射线AB的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
2.Rt△ABC中,∠C=90°,AB=10,AC=6,以C为圆心作⊙C和AB相切,则⊙C的半径长为( )
A.8 B.4 C.9.6 D.4.8
3.⊙O内最长弦长为,直线与⊙O相离,设点O到的距离为,则与的关系是( )
A.= B.> C.> D.<
4.以三角形的一边长为直径的圆切三角形的另一边,则该三角形为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形
5.菱形对角线的交点为O,以O为圆心,以O到菱形一边的距离为半径的圆与其他几边的关系为( )
A.相交 B.相切 C.相离 D.不能确定
6.⊙O的半径为6,⊙O的一条弦AB为6,以3为半径的同心圆与直线AB的位置关系是( )
A.相离 B.相交 C.相切 D.不能确定
7.下列四边形中一定有内切圆的是( )
A.直角梯形 B.等腰梯形 C.矩形 D.菱形
8.已知△ABC的内切圆O与各边相切于D、E、F,那么点O是△DEF的( )
A.三条中线交点 B.三条高的交点
C.三条角平分线交点 D.三条边的垂直平分线的交点
9.给出下列命题:
①任一个三角形一定有一个外接圆,并且只有一个外接圆;
②任一个圆一定有一个内接三角形,并且只有一个内接三角形;
③任一个三角形一定有一个内切圆,并且只有一个内切圆;
④任一个圆一定有一个外切三角形,并且只有一个外切三角形.
其中真命题共有( )
A.1个 B.2个 C.3个 D.4个
二、证明题
1.如图,已知⊙O中,AB是直径,过B点作⊙O的切线BC,连结CO.若AD∥OC交⊙O于D.求证:CD是⊙O的切线.
2.已知:如图,同心圆O,大圆的弦AB=CD,且AB是小圆的切线,切点为E.求证:CD是小圆的切线.
3.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,⊙O的半径为3.
(1)当圆心O与C重合时,⊙O与AB的位置关系怎样?
(2)若点O沿CA移动时,当OC为多少时?⊙C与AB相切?
4.如图,直角梯形ABCD中,∠A=∠B=90°,AD∥BC,E为AB上一点,DE平分∠ADC,CE平分∠BCD,以AB为直径的圆与边CD有怎样的位置关系?
5.有一块锐角三角形木板,现在要用它截成一个最大面积的圆形木板,问怎样才能使圆形木板面积最大?
6.如图,AB是⊙O直径,⊙O过AC的中点D,DE⊥BC,垂足为E.
(1)由这些条件,你能得出哪些结论?(要求:不准标其他字母,找结论过程中所连的辅助线不能出现在结论中,不写推理过程,写出4个结论即可)
(2)若∠ABC为直角,其他条件不变,除上述结论外你还能推出哪些新的正确结论?并画出图形.(要求:写出6个结论即可,其他要求同(1))
7.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.若以C为圆心,R为半径所作的圆与斜边AB只有一个公共点,则R的取值范围是多少?
8.如图,有一块锐角三角形木板,现在要把它截成半圆形板块(圆心在BC上),问怎样截取才能使截出的半圆形面积最大?(要求说明理由)
9.如图,直线ι1、ι2、ι3表示相互交叉的公路.现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有几处?
第一课时参考答案
1.相交 2.60 3.如OA⊥PA,OB⊥PB,AB⊥OP等. 4.0≤d<4. 5.65°
6. 146°,60°,86° 7.A 8.B 9.C 10.C 11.D 12.B
13.(1)AD⊥CD.理由:连接OC,则OC⊥CD.
∵OA=OC,∴∠OAC=∠OCA,
又∠OAC= ∠DAC,∴∠DAC=∠OCA,∴AD∥OC,∴AD⊥CD.
(2)连接BC,则∠ACB=90°由(1)得∠ADC=∠ACB,
又∠DAC=∠CAB.∴△ACD∽△ABC,
∴,即AC2=AD·AB=80,故AC=.
14.(1)相等.理由:连接OA,则∠PAO=90°.
∵OA=OB,∴∠OAB=∠B=30°, ∴∠AOP=60°,∠P=90°-60°=30°,
∴∠P=∠B,∴AB=AP,
(2)∵tan∠APO=,
∴OA=PA, tan∠APO=,
∴BC=2OA=2,即半圆O的直径为2.
15.(1)平分.证明:连接OT,∵PT切⊙O于T,
∴OT⊥PT,故∠OTA=90°,
从而∠OBT=∠OTB=90°-∠ATB=∠ABT.即BT平分∠OBA.
(2)过O作OM⊥BC于M,则四边形OTAM是矩形,
故OM=AT=4,AM=OT=5.在Rt△OBM中, OB=5,OM=4,
故BM==3,从而AB=AM-BM=5-3=2.
16.作出△ABC的内切圆⊙O,沿⊙O的圆周剪出一个圆,其面积最大.
17.由已知得:OA=OE,∠OAC=∠OEC,又OC公共,故△OAC≌OEC,
同理,△OBD ≌△OED,由此可得∠AOC=∠EOC,∠BOD=∠EOD,
从而∠COD=90°,∠AOC=∠BDO.
根据这些写如下结论:
①角相等:∠AOC=∠COE=∠BDO=∠EDO,∠ACO=∠ECO=∠DOE=∠DOB,
∠A=∠B=∠OEC=∠OED,
②边相等:AC=CE,DE=DB,OA=OB=OE;
③全等三角形:△OAC≌△OEC,△OBD≌△OED;
④相似三角形:△AOC∽△EOC∽△EDO∽△BDO∽△ODC.
18. (1)PC与⊙D相切,理由:令x=0,得y=-8,故P(0,-8);令y=0,得x=-2,
故C(-2,0),故OP=8,OC=2,CD=1,
∴CD==3,
又PC=,
∴PC2+CD2=9+72=81=PD2.
从而∠PCD=90°,故PC与⊙D相切.
(2)存在.点E(,-12)或(-,-4),使S△EOP=4S△CDO.
设E点坐标为(x,y),过E作EF⊥y轴于F,则EF=│x│.
∴S△POE=PO·EF=4│x│.
∵S△CDO=CO·DO=.
∴4│x│=4,│x│=,x=±,
当x=- 时,y=-2×(-)-8=-4 ;
当x= 时,y=-2×-8=-12 .
故E点坐标为(-,-4)或(,-12).
第二课时参考答案
一、1-5 A D C B B ; 6-9 C D D B
二、1.提示:连结OC,证△AOC与△BOC全等
2.作垂直证半径,弦心距相等
3.①垂直三角形的高,用面积方法求;②△AOE∽△ABC即可
4.用角平分线定理证明EF=EA=EB即可
5.做三角形的内切圆
6.①DE与⊙O相切,AB=BC,DE2+CE2=CD2,∠C+∠CDE=90°
②BC是⊙O的切线,有DE=1/2AB等.
7.R=2.4或3
9.4
