【课件】2.1 直线的倾斜角与斜率 数学-RJ·A-选择性必修第一册(共41张PPT)
文档属性
| 名称 | 【课件】2.1 直线的倾斜角与斜率 数学-RJ·A-选择性必修第一册(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 00:00:00 | ||
图片预览










文档简介
(共41张PPT)
数学-RJ·A-选择性必修第一册
第二章 直线和圆的方程
2.1 直线的倾斜角与斜率
学习目标
1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素.
2.理解直线的倾斜角和斜率的概念,经历用代数方法刻画直线斜率的过程.
3.掌握过两点的直线斜率的计算公式.
4.能根据直线的斜率判定两条直线平行或垂直.
重点:斜率的概念,用代数方法刻画直线斜率的过程,过两点的直线斜率的计算公式,根据斜率判断两条直线平行或垂直.
难点:直线的斜率与它的倾斜角之间的关系,根据斜率判断两条直线互相垂直.
知识梳理
当直线与轴相交时,我们以轴为基准,轴正向与直线向上的方向之间所成的角α叫做直线l的倾斜角(angle of inclination).图中直线的倾斜角为锐角,直线的倾斜角为钝角.当直线与轴平行或重合时,我们规定它的倾斜角为0°.因此,直线的倾斜角的取值范围为
一、直线的倾斜角
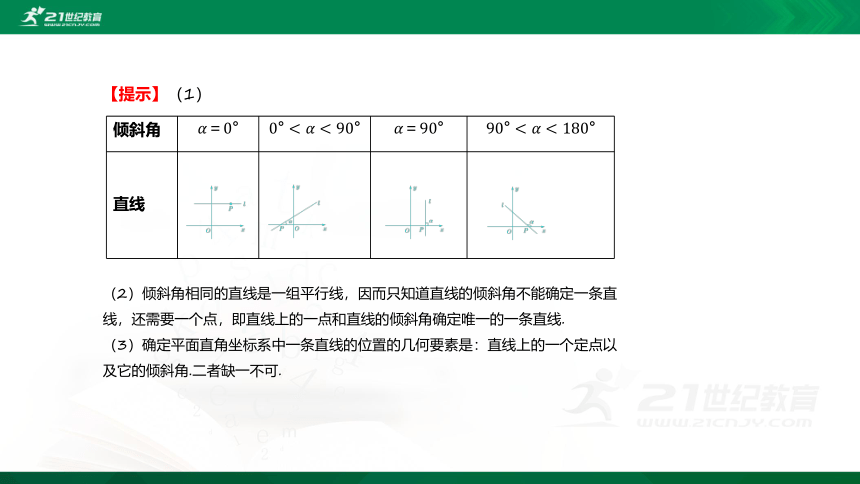
倾斜角
直线
【提示】(1)
(2)倾斜角相同的直线是一组平行线,因而只知道直线的倾斜角不能确定一条直线,还需要一个点,即直线上的一点和直线的倾斜角确定唯一的一条直线.
(3)确定平面直角坐标系中一条直线的位置的几何要素是:直线上的一个定点以及它的倾斜角.二者缺一不可.
二、直线的斜率
我们把一条直线的倾斜角的正切值叫做这条直线的斜率(slope).斜率常用小写字母表示,即
【注意】
倾斜角是90°的直线没有斜率,倾斜角不是90°的直线都有斜率.
【提示】直线的斜率与倾斜角之间的关系
当直线的倾斜角时,斜率,直线与轴平行或重合;
当时,斜率,且值随着倾斜角的增大而增大;
当时,斜率不存在(此时直线是存在的,直线与轴垂直);当时,斜率,且值随着倾斜角的增大而增大.
如果直线经过两点(),那么可得如下的斜率公式:
【提示】对斜率公式k= 的理解:
(1)当时,公式右边无意义,直线的斜率不存在,倾斜角为90°.所以斜率公式的适用范围不包括倾斜角的情况.凡是在研究直线的斜率问题时,一定要注意斜率的存在与不存在两种情况.
(2)斜率公式中k的值与两点在该直线上的位置无关,即在直线上任取不同的两点,其斜率均不变.
(3)斜率公式中两纵坐标和两横坐标在公式中的次序可以同时调换,也就是说,如果分子是,分母必须是;如果分子是,分母必须是,即k= = .
(4)若,则直线与x轴平行或重合,斜率=0.
三、两条直线平行的判定
对于斜率分别为的两条直线,有
.
显然,当时,直线的斜率不存在,此时.
若直线重合,此时仍然有
【注意】是的必要不充分条件.
二、两条直线垂直的判定
如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于;反之,如果两条直线的斜率之积等于,那么它们互相垂直.即
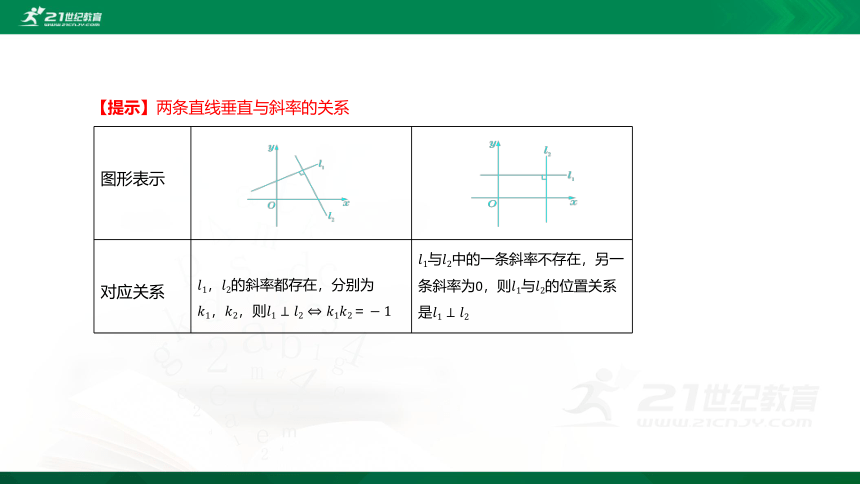
【提示】两条直线垂直与斜率的关系
图形表示
对应关系 的斜率都存在,分别为,则 与中的一条斜率不存在,另一条斜率为0,则的位置关系是
常考题型
一、直线的倾斜角与斜率
1.求直线的倾斜角或斜率
◆求直线斜率的两种方法
1.利用定义:已知直线的倾斜角为α,且α≠90°,则k=tan α.
2.利用斜率公式:k= (x1≠x2).
【注意】
利用两点斜率的公式时,两点的横坐标不能相等,否则,直线斜率不存在.
◆求直线倾斜角的方法
1.定义法:根据题意画出图形,结合倾斜角的定义求出倾斜角.
2.利用tan α=k求倾斜角.
训练题
1.[2020·安徽师范大学附属中学高二期中]已知点A(2,-3),B(-3,-2),
直线l过点P(1,1),且与线段AB相交,则直线l的斜率k的取值范围是( )
A.k≥或k≤4 B.k≥或k≤C.4≤k≤D.≤k≤4
2.[2020·广东湛江高一联考]设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转45°,得到直线l1,则直线l1的倾斜角为 ( )
A.α+45° B.α-135° C.135°-α D.α+45°或α-135°
3.[2020·湖南长沙长郡中学高一期中]下列四条直线中,其倾斜角最大的是
( )
A.2x-y+1=0 B.x+2y+3=0 C.x+y+1=0 D.x+1=0
A
D
B
2.三点共线问题
例2 已知A(a,2),B(5,1),C(-4,2a)三点在同一条直线上,求a的值.
◆利用斜率法证明已知坐标的三点共线
证明已知坐标的三点共线,利用斜率法是最简单的方法.若两直线AB,BC的斜率相等,则A,B,C三点共线;反过来,若A,B,C三点共线,则直线AB,BC的斜率相等(斜率存在时),或直线AB,BC的斜率都不存在.
训练题
1.[2020·广东江门高一月考]已知A(-3,-5),B(1,3),
C(5,11)三点,这三点 (填“是”或“否”)在
同一直线上.
2.[2020·江西景德镇一中高一期中]设A(1,1),B(2,a),
C(b,3)三点共线,且a,b∈N* ,则a-b的值为 ( )
A.1 B.-1 C.1或-1 D.无法确定
是
C
3.斜率模型的几何意义
例3 已知实数x,y满足y=x2-2x+2(-1≤x≤1),试求的
最大值和最小值.
【解题提示】 的最大值和最小值可以看成过两点
(-2,-3),(x,y)的直线的斜率的最大值和最小值.
【解】如图,由的几何意义可知,它表示经过定点P(-2,-3)与曲线段AB上任一点(x,y)的直线的斜率k,由图可知kPA≤k≤kPB,由已知可得A(1,1),B(-1,5).
则kPA==,kPB==8.
∴≤k≤8,∴的最大值为8,最小值为.
训练题
已知实数x,y满足2x+y=8,且2≤x≤3,求的最大值和最小值.
解:如图所示,由已知,点在线段AB上运动,其中,而=,其几何意义为直线OP的斜率.由图可知kOB≤kOP≤kOA,而kOB=,kOA=2.
故所求的最大值为2,最小值为.
二、两条直线平行、垂直的判定与应用
1.两条直线平行的判定与应用
例4 判断下列各小题中的直线l1与l2是否平行.
(1)经过点经过点
(2)的斜率为1,经过点
(3)经过点经过点;
(4)经过点经过点
◆判断两条直线平行的方法
1.判断两条直线的斜率是否存在.
2.当直线的斜率存在时,利用斜率公式求出两直线的斜率,若斜率相等,则进一步判断两直线是重合还是平行.
3.若两直线的斜率都不存在(同一直线上两点的横坐标相等),且两直线所过点的横坐标不相等,则两直线平行.
特殊情况下的两条直线平行的判定:
若两条直线(不重合)的倾斜角都为90°,则它们互相平行.
训练题
1.[2020·安徽阜阳市红旗中学高一期末]已知直线x+a2y+6=0与直线(a-2)x+3ay+2a=0平行,则a的值为 ( )
A.0或3或-1 B.0或3 C.3或-1 D.0或-1
2.[2020·甘肃武威六中高一月考]已知倾斜角为45°的直线经过A(2,4),B(1,m)两点,则m= ( )
A.3 B.-3 C.5 D.-1
D
A
2.两条直线垂直的判定与应用
例5 判断下列各组中的直线l1与l2是否垂直:
(1)l1经过点A(-1,-2),B(1,2),l2经过点M(-2,-1),
N(2,1);
(2)l1的斜率为-10,l2经过点A(10,2),B(20,3);
(3)l1经过点A(3,4),B(3,100),l2经过点M(-10,40),
N(10,40).
【解题提示】求出斜率,利用l1⊥l2?k1k2=-1或一条直线斜率为0,
另一条斜率不存在来判断.
◆利用斜率公式来判定两直线垂直的方法
1.一看:就是先看其中一条直线的两点的横坐标是否相等,若相等,则直线的斜率不存在.再看另一条直线的两点的纵坐标是否相等,若相等,则垂直,若不相等,则进行第二步.
2.二代:将点的坐标代入斜率公式.
3.三求值:计算斜率的值,进行判断.尤其是点的坐标中含有参数时,应用斜率公式时要对参数进行讨论.
A
C
三、两条直线平行、垂直的综合问题
例6 在平面直角坐标系中,四边形OPQR的顶点按逆时针顺序依次为O(0,0),P(1,t),Q(1-2t,2+t),R(-2t,2),其中t>0.试判断四边形OPQR的形状.
【解】由斜率公式得kOP==t,同理kQR=t,kOR=-,kPQ=-,
所以kOP=kQR,kOR=kPQ.从而OP平行于QR,OR平行于PQ.
所以四边形OPQR为平行四边形.
又kOP·kOR=-1,所以OP⊥OR.
故四边形OPQR为矩形.
◆利用两条直线平行或垂直判定几何图形形状的步骤
训练题
1.[2020·浙江杭州学军中学高二期中]已知直线l1,l2的斜率k1,k2是关于k的方程2k2-3k-b=0的两个实根,若l1⊥l2,则b= ;若l1∥l2,则b= .
2
2.已知A(-4,3),B(2,5),C(6,3),D(-3,0)四点,若顺次连接A,B,C,D四点,试判定四边形ABCD的形状.
小结
1. 直线的倾斜角
(1)定义:当直线l与x轴相交时,以x轴为基准,x轴正向与直线l向上的方向之间所成的角α叫做直线l的倾斜角.
当直线l与x轴平行或重合时,规定它的倾斜角为0°.
(2)范围:直线的倾斜角α的取值范围为0°≤α<180°.
3. 两条直线平行的判定
①直线l1,l2的斜率分别为k1,k2,则l1∥l2 α1=α2 k1=k2;
②直线l1,l2的斜率都不存在,则α1=α2=90° l1∥l2.
4. 两条直线垂直的判定
①直线l1,l2的斜率分别为k1,k2,则l1⊥l2 k1k2=-1;
②直线l1,l2中一条斜率不存在,即倾斜角为90°,另一条的斜率为0,则l1⊥l2
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·A-选择性必修第一册
第二章 直线和圆的方程
2.1 直线的倾斜角与斜率
学习目标
1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素.
2.理解直线的倾斜角和斜率的概念,经历用代数方法刻画直线斜率的过程.
3.掌握过两点的直线斜率的计算公式.
4.能根据直线的斜率判定两条直线平行或垂直.
重点:斜率的概念,用代数方法刻画直线斜率的过程,过两点的直线斜率的计算公式,根据斜率判断两条直线平行或垂直.
难点:直线的斜率与它的倾斜角之间的关系,根据斜率判断两条直线互相垂直.
知识梳理
当直线与轴相交时,我们以轴为基准,轴正向与直线向上的方向之间所成的角α叫做直线l的倾斜角(angle of inclination).图中直线的倾斜角为锐角,直线的倾斜角为钝角.当直线与轴平行或重合时,我们规定它的倾斜角为0°.因此,直线的倾斜角的取值范围为
一、直线的倾斜角
倾斜角
直线
【提示】(1)
(2)倾斜角相同的直线是一组平行线,因而只知道直线的倾斜角不能确定一条直线,还需要一个点,即直线上的一点和直线的倾斜角确定唯一的一条直线.
(3)确定平面直角坐标系中一条直线的位置的几何要素是:直线上的一个定点以及它的倾斜角.二者缺一不可.
二、直线的斜率
我们把一条直线的倾斜角的正切值叫做这条直线的斜率(slope).斜率常用小写字母表示,即
【注意】
倾斜角是90°的直线没有斜率,倾斜角不是90°的直线都有斜率.
【提示】直线的斜率与倾斜角之间的关系
当直线的倾斜角时,斜率,直线与轴平行或重合;
当时,斜率,且值随着倾斜角的增大而增大;
当时,斜率不存在(此时直线是存在的,直线与轴垂直);当时,斜率,且值随着倾斜角的增大而增大.
如果直线经过两点(),那么可得如下的斜率公式:
【提示】对斜率公式k= 的理解:
(1)当时,公式右边无意义,直线的斜率不存在,倾斜角为90°.所以斜率公式的适用范围不包括倾斜角的情况.凡是在研究直线的斜率问题时,一定要注意斜率的存在与不存在两种情况.
(2)斜率公式中k的值与两点在该直线上的位置无关,即在直线上任取不同的两点,其斜率均不变.
(3)斜率公式中两纵坐标和两横坐标在公式中的次序可以同时调换,也就是说,如果分子是,分母必须是;如果分子是,分母必须是,即k= = .
(4)若,则直线与x轴平行或重合,斜率=0.
三、两条直线平行的判定
对于斜率分别为的两条直线,有
.
显然,当时,直线的斜率不存在,此时.
若直线重合,此时仍然有
【注意】是的必要不充分条件.
二、两条直线垂直的判定
如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于;反之,如果两条直线的斜率之积等于,那么它们互相垂直.即
【提示】两条直线垂直与斜率的关系
图形表示
对应关系 的斜率都存在,分别为,则 与中的一条斜率不存在,另一条斜率为0,则的位置关系是
常考题型
一、直线的倾斜角与斜率
1.求直线的倾斜角或斜率
◆求直线斜率的两种方法
1.利用定义:已知直线的倾斜角为α,且α≠90°,则k=tan α.
2.利用斜率公式:k= (x1≠x2).
【注意】
利用两点斜率的公式时,两点的横坐标不能相等,否则,直线斜率不存在.
◆求直线倾斜角的方法
1.定义法:根据题意画出图形,结合倾斜角的定义求出倾斜角.
2.利用tan α=k求倾斜角.
训练题
1.[2020·安徽师范大学附属中学高二期中]已知点A(2,-3),B(-3,-2),
直线l过点P(1,1),且与线段AB相交,则直线l的斜率k的取值范围是( )
A.k≥或k≤4 B.k≥或k≤C.4≤k≤D.≤k≤4
2.[2020·广东湛江高一联考]设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转45°,得到直线l1,则直线l1的倾斜角为 ( )
A.α+45° B.α-135° C.135°-α D.α+45°或α-135°
3.[2020·湖南长沙长郡中学高一期中]下列四条直线中,其倾斜角最大的是
( )
A.2x-y+1=0 B.x+2y+3=0 C.x+y+1=0 D.x+1=0
A
D
B
2.三点共线问题
例2 已知A(a,2),B(5,1),C(-4,2a)三点在同一条直线上,求a的值.
◆利用斜率法证明已知坐标的三点共线
证明已知坐标的三点共线,利用斜率法是最简单的方法.若两直线AB,BC的斜率相等,则A,B,C三点共线;反过来,若A,B,C三点共线,则直线AB,BC的斜率相等(斜率存在时),或直线AB,BC的斜率都不存在.
训练题
1.[2020·广东江门高一月考]已知A(-3,-5),B(1,3),
C(5,11)三点,这三点 (填“是”或“否”)在
同一直线上.
2.[2020·江西景德镇一中高一期中]设A(1,1),B(2,a),
C(b,3)三点共线,且a,b∈N* ,则a-b的值为 ( )
A.1 B.-1 C.1或-1 D.无法确定
是
C
3.斜率模型的几何意义
例3 已知实数x,y满足y=x2-2x+2(-1≤x≤1),试求的
最大值和最小值.
【解题提示】 的最大值和最小值可以看成过两点
(-2,-3),(x,y)的直线的斜率的最大值和最小值.
【解】如图,由的几何意义可知,它表示经过定点P(-2,-3)与曲线段AB上任一点(x,y)的直线的斜率k,由图可知kPA≤k≤kPB,由已知可得A(1,1),B(-1,5).
则kPA==,kPB==8.
∴≤k≤8,∴的最大值为8,最小值为.
训练题
已知实数x,y满足2x+y=8,且2≤x≤3,求的最大值和最小值.
解:如图所示,由已知,点在线段AB上运动,其中,而=,其几何意义为直线OP的斜率.由图可知kOB≤kOP≤kOA,而kOB=,kOA=2.
故所求的最大值为2,最小值为.
二、两条直线平行、垂直的判定与应用
1.两条直线平行的判定与应用
例4 判断下列各小题中的直线l1与l2是否平行.
(1)经过点经过点
(2)的斜率为1,经过点
(3)经过点经过点;
(4)经过点经过点
◆判断两条直线平行的方法
1.判断两条直线的斜率是否存在.
2.当直线的斜率存在时,利用斜率公式求出两直线的斜率,若斜率相等,则进一步判断两直线是重合还是平行.
3.若两直线的斜率都不存在(同一直线上两点的横坐标相等),且两直线所过点的横坐标不相等,则两直线平行.
特殊情况下的两条直线平行的判定:
若两条直线(不重合)的倾斜角都为90°,则它们互相平行.
训练题
1.[2020·安徽阜阳市红旗中学高一期末]已知直线x+a2y+6=0与直线(a-2)x+3ay+2a=0平行,则a的值为 ( )
A.0或3或-1 B.0或3 C.3或-1 D.0或-1
2.[2020·甘肃武威六中高一月考]已知倾斜角为45°的直线经过A(2,4),B(1,m)两点,则m= ( )
A.3 B.-3 C.5 D.-1
D
A
2.两条直线垂直的判定与应用
例5 判断下列各组中的直线l1与l2是否垂直:
(1)l1经过点A(-1,-2),B(1,2),l2经过点M(-2,-1),
N(2,1);
(2)l1的斜率为-10,l2经过点A(10,2),B(20,3);
(3)l1经过点A(3,4),B(3,100),l2经过点M(-10,40),
N(10,40).
【解题提示】求出斜率,利用l1⊥l2?k1k2=-1或一条直线斜率为0,
另一条斜率不存在来判断.
◆利用斜率公式来判定两直线垂直的方法
1.一看:就是先看其中一条直线的两点的横坐标是否相等,若相等,则直线的斜率不存在.再看另一条直线的两点的纵坐标是否相等,若相等,则垂直,若不相等,则进行第二步.
2.二代:将点的坐标代入斜率公式.
3.三求值:计算斜率的值,进行判断.尤其是点的坐标中含有参数时,应用斜率公式时要对参数进行讨论.
A
C
三、两条直线平行、垂直的综合问题
例6 在平面直角坐标系中,四边形OPQR的顶点按逆时针顺序依次为O(0,0),P(1,t),Q(1-2t,2+t),R(-2t,2),其中t>0.试判断四边形OPQR的形状.
【解】由斜率公式得kOP==t,同理kQR=t,kOR=-,kPQ=-,
所以kOP=kQR,kOR=kPQ.从而OP平行于QR,OR平行于PQ.
所以四边形OPQR为平行四边形.
又kOP·kOR=-1,所以OP⊥OR.
故四边形OPQR为矩形.
◆利用两条直线平行或垂直判定几何图形形状的步骤
训练题
1.[2020·浙江杭州学军中学高二期中]已知直线l1,l2的斜率k1,k2是关于k的方程2k2-3k-b=0的两个实根,若l1⊥l2,则b= ;若l1∥l2,则b= .
2
2.已知A(-4,3),B(2,5),C(6,3),D(-3,0)四点,若顺次连接A,B,C,D四点,试判定四边形ABCD的形状.
小结
1. 直线的倾斜角
(1)定义:当直线l与x轴相交时,以x轴为基准,x轴正向与直线l向上的方向之间所成的角α叫做直线l的倾斜角.
当直线l与x轴平行或重合时,规定它的倾斜角为0°.
(2)范围:直线的倾斜角α的取值范围为0°≤α<180°.
3. 两条直线平行的判定
①直线l1,l2的斜率分别为k1,k2,则l1∥l2 α1=α2 k1=k2;
②直线l1,l2的斜率都不存在,则α1=α2=90° l1∥l2.
4. 两条直线垂直的判定
①直线l1,l2的斜率分别为k1,k2,则l1⊥l2 k1k2=-1;
②直线l1,l2中一条斜率不存在,即倾斜角为90°,另一条的斜率为0,则l1⊥l2
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
