【课件】§1 生活中的变量关系 §2函数 2.1函数概念 高中数学-北师大版-必修第一册-第二章(共48张PPT)
文档属性
| 名称 | 【课件】§1 生活中的变量关系 §2函数 2.1函数概念 高中数学-北师大版-必修第一册-第二章(共48张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-05 18:04:35 | ||
图片预览











文档简介
(共48张PPT)
高中数学-北师大版-必修第一册
§1 生活中的变量关系
§2 函 数
2.1 函数概念
第二章 函 数
学习目标
1.能够认识和发现生活中变量间的依赖关系.
2.能利用初中所学函数知识对依赖关系是不是函数关系进行判断.
3.用集合语言和对应关系刻画函数,建立完整的函数概念.
4.体会集合语言和对应关系在刻画函数概念中的作用.
5.了解构成函数的要素,能求简单函数的定义域.
重点:变量间依赖关系和函数关系的区别,函数的概念.
难点:对抽象符号f(x)的理解.
知识梳理
1.分段函数
2.函数的概念
例1
一 函数关系的判断
<1>判断所给关系是不是函数
常考题型
【解析】 对于A,集合A中元素2在B中没有元素对应,不是函数;
对于B,集合A中任一元素在B中都有唯一元素对应,是函数;
对于C,集合A中元素3在B中没有元素对应,不是函数;
对于D,集合A中元素2在B中没有元素对应,不是函数.
【答案】 B
判断一个对应关系是不是函数的方法
一个对应关系是不是函数,主要从以下三个方面去判断
(1)A,B是不是非空数集;
(2)A中任何一个元素在B中是否有元素与其对应;
(3)A中任何一个元素在B中的对应元素是否唯一.
解题归纳
[2020·浙江温州高一期末]设集合M={x|0≤x≤2},N={y|0≤y≤2},那么下图中,能表示集合M到集合N的函数关系的是 ( )
A.①②③④ B.①②③ C.②③ D.②
训练题
1.
C
① ② ③ ④
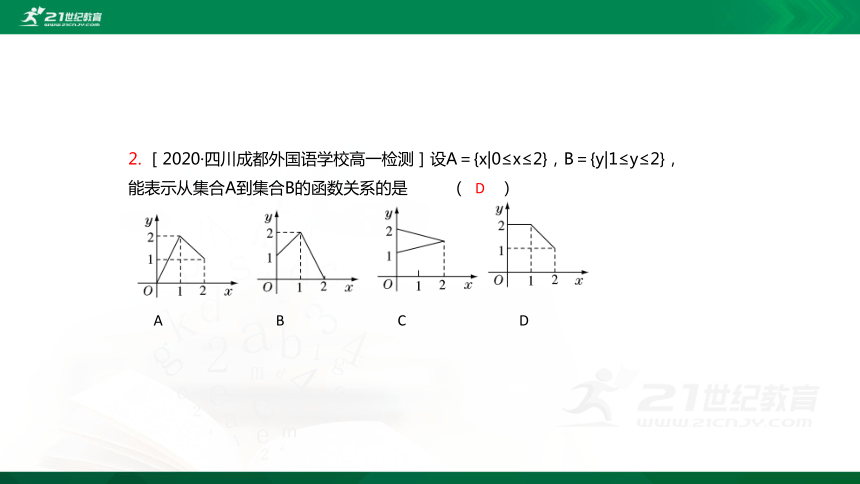
2. [2020·四川成都外国语学校高一检测]设A={x|0≤x≤2},B={y|1≤y≤2},能表示从集合A到集合B的函数关系的是 ( )
A B C D
D
判断一个图形是不是函数图象的常用方法
(1)看图形对应的x轴上的任意一个x是否都有唯一的y与之对应,若是,则此图形可能是函数的图象;若至少有一个x值存在两个或两个以上的y值与之对应,则此图形一定不是函数的图象.
(2)要关注函数的定义域、值域与图形中所示的定义域(图形正对着的x轴上的实数)、值域(图形正对着的y轴上的实数)是否一致.
解题归纳
例2
<2>判断两个函数是否相同
判断两函数相同的方法及注意点
(1)方法:判断两函数是否相同时,要遵循定义域优先的原则,即要先求定义域.若定义域不同,则不相同;若定义域相同,再化简函数的解析式,看对应关系是否相同.
(2)两个注意点
①函数的表示:与变量用什么字母表示无关;
②解析式的化简:在化简解析式时,必须是等价变形.
解题归纳
训练题
D
训练题
C
例3
二 函数定义域问题
<1>已知解析式求定义域
求函数定义域的常用依据
(1)若f(x)是分式,则分母不为零;
(2)若f(x)是偶次根式,则被开方数大于或等于零;
(3)若函数y=(f(x))0,则f(x)≠0;
(4)若f(x)是由几个式子构成的,则函数的定义域要使各个式子都有意义;
(5)若f(x)是实际问题的解析式,则函数的定义域应使实际问题有意义.
解题归纳
训练题
1.
A
2.
D
<2>求抽象函数、复合函数的定义域
例4
求抽象函数或复合函数定义域的方法
(1)已知f(x)的定义域为A,求f(φ(x))的定义域,其实质是已知φ(x)的取值范围为A,求x的取值范围.
(2)已知f(φ(x))的定义域为B,求f(x)的定义域,其实质是已知f(φ(x))中x的取值范围为B,求φ(x)的取值范围(值域).
解题归纳
训练题
1.
2.
C
C
求抽象函数或复合函数的定义域时需明确的三个问题
(1)函数f(x)的定义域是指x的取值所成的集合.
(2)函数f(φ(x))的定义域是指x的取值范围,而不是φ(x)的取值范围.
(3)f(t),f(φ(x)),f(h(x))三个函数中的t,φ(x),h(x)在对应关系f下的取值范围相同.
解题归纳
<3>已知函数的定义域求参数
例5
训练题
1.
2.
D
(3,+∞)
<4>应用问题中的定义域
例6
如图所示,用长为1的铁丝围成下边为矩形、上边为半圆形的框架,若半圆的半径为,求此框架围成的面积与的函数解析式,并写出它的定义域.
训练题
D
三 函数求值或函数的值域问题
<1>函数求值问题
例7
[2020·黑龙江大庆实验中学高二检测] 若f(x)=x2-2x,则f(f(f(1)))=( )
A.1 B.2 C.3 D.4
【解题提示】 依次把自变量代入函数关系式,由内向外求值即可.
【解析】 由f(x)=x2-2x,可得f(1)=1-2=-1,所以f(f(1))=f(-1)=1+2=3,f(f(f(1)))=f(3)=9-6=3.
【答案】 C
训练题
15
A
<2>函数的值域问题
例8
例9
求函数值域的方法
求函数值域的常用方法:观察法、配方法、分离常数法、换元法、判别式法、反表示法、中间变量法.
(1)观察法:通过对函数解析式的简单变形,利用熟知的基本函数的值域,或利用函数图象的“最高点”和“最低点”观察函数的值域.如函数y=的值域为{y|0(2)配方法:求形如F(x)=a(f(x))2 +bf(x)+c(a≠0)的函数的值域可用配方法,但要注意f(x)的取值范围.如求函数y=x++3的值域,因为y=(+1)2+2≥3,故所求值域为{y|y≥3}.同时要注意在给定区间上二次函数最值的求法.
解题归纳
(3)分离常数法:形如y=(ac≠ 0,ad≠bc)的函数常用分离常数法求值域.转化过程为y= =+ ,其结论是.
(4)换元法:形如y=ax+b+(a≠0)的函数常用换元法求值域,即先令t= ,求出x,并注明t的取值范围,再代入上式将y表示成关于t的二次函数,最后用配方法求值域.
注意:分离常数法的目的是将分式函数变为反比例型函数,换元法的目的是将函数变为二次函数,即将函数解析式变为熟悉的简单函数类型求值域.
解题归纳
(5)判别式法:形如y=(a,d中至少有一个不为零)的值域,常把函数转化成关于x的二次方程F(x,y)=0,通过方程有实根,判别式Δ≥0,求出y的取值范围.
(6)反表示法:根据函数解析式反解出x,根据x的取值范围转化为关于y的不等式求解.
(7)中间变量法:根据函数解析式确定一个已知范围的中间变量(如x2),用y表示出该中间变量,根据中间变量的取值范围转化为关于y的不等式求解.
解题归纳
训练题
{ f(x)| f(x)≠1}
<3>已知值域求参数
例9
已知函数值域求参数的解题提示
(1)注意调整思维方向,根据值域的含义将参数问题转化为方程的解或不等式的解集问题.
(2)根据方程的解或不等式的解集情况来确定参数的值或取值范围.
解题归纳
训练题
D
[2020·四川阆中中学高一检测] 函数f (x)=x2-4x-6的定义域为[0,m],值域为[-10,-6],则m的取值范围是( )
A.[0,4] B.[4,6] C.[2,6] D.[2,4]
四 对应关系问题
例10
实验测得音速与气温的一些数据如下表所示:
气温x/℃ 0 5 10 15 20
音速y/(米/秒) 331 334 337 340 343
(1)根据表内数据作图,由图可看出变量 随 的变化而变化.
(2)用x表示y的关系式为 .
(3)气温为22 ℃时,某人看到烟花燃放5秒后才听到声响,那么此人与燃放的烟花所在地相距约 米.
在一次百米赛跑中,甲、乙两人的路程与时间的关系如图所示,那么可以知道:
(1)甲、乙两人中先到达终点的是 .
(2)乙在这次赛跑中的速度为 m/s.
训练题
甲
8
小结
函数的概念
理解函数的概念需注意:
(1)A,B必须为非空数集,定义域或值域为空集的函数是不存在的.
(2)两个非空数集间的对应关系能否构成函数,主要看是否满足“三性”:任意性、存在性、唯一性.这是因为函数概念中明确要求对于非空数集A中的任意一个(任意性)元素x,在非空数集B中都有(存在性)唯一(唯一性)的元素y与之对应.这“三性”只要有一个不满足便不能构成函数.
(3)集合A是函数的定义域,因为给定A中每一个x值都有唯一的y值与之对应;集合B不一定是函数的值域,因为B中的元素可以没有与之对应者,即{f(x)|x∈A}B.
(4)在函数定义中,我们用符号y=f(x)表示函数,而不是“f乘x”.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
高中数学-北师大版-必修第一册
§1 生活中的变量关系
§2 函 数
2.1 函数概念
第二章 函 数
学习目标
1.能够认识和发现生活中变量间的依赖关系.
2.能利用初中所学函数知识对依赖关系是不是函数关系进行判断.
3.用集合语言和对应关系刻画函数,建立完整的函数概念.
4.体会集合语言和对应关系在刻画函数概念中的作用.
5.了解构成函数的要素,能求简单函数的定义域.
重点:变量间依赖关系和函数关系的区别,函数的概念.
难点:对抽象符号f(x)的理解.
知识梳理
1.分段函数
2.函数的概念
例1
一 函数关系的判断
<1>判断所给关系是不是函数
常考题型
【解析】 对于A,集合A中元素2在B中没有元素对应,不是函数;
对于B,集合A中任一元素在B中都有唯一元素对应,是函数;
对于C,集合A中元素3在B中没有元素对应,不是函数;
对于D,集合A中元素2在B中没有元素对应,不是函数.
【答案】 B
判断一个对应关系是不是函数的方法
一个对应关系是不是函数,主要从以下三个方面去判断
(1)A,B是不是非空数集;
(2)A中任何一个元素在B中是否有元素与其对应;
(3)A中任何一个元素在B中的对应元素是否唯一.
解题归纳
[2020·浙江温州高一期末]设集合M={x|0≤x≤2},N={y|0≤y≤2},那么下图中,能表示集合M到集合N的函数关系的是 ( )
A.①②③④ B.①②③ C.②③ D.②
训练题
1.
C
① ② ③ ④
2. [2020·四川成都外国语学校高一检测]设A={x|0≤x≤2},B={y|1≤y≤2},能表示从集合A到集合B的函数关系的是 ( )
A B C D
D
判断一个图形是不是函数图象的常用方法
(1)看图形对应的x轴上的任意一个x是否都有唯一的y与之对应,若是,则此图形可能是函数的图象;若至少有一个x值存在两个或两个以上的y值与之对应,则此图形一定不是函数的图象.
(2)要关注函数的定义域、值域与图形中所示的定义域(图形正对着的x轴上的实数)、值域(图形正对着的y轴上的实数)是否一致.
解题归纳
例2
<2>判断两个函数是否相同
判断两函数相同的方法及注意点
(1)方法:判断两函数是否相同时,要遵循定义域优先的原则,即要先求定义域.若定义域不同,则不相同;若定义域相同,再化简函数的解析式,看对应关系是否相同.
(2)两个注意点
①函数的表示:与变量用什么字母表示无关;
②解析式的化简:在化简解析式时,必须是等价变形.
解题归纳
训练题
D
训练题
C
例3
二 函数定义域问题
<1>已知解析式求定义域
求函数定义域的常用依据
(1)若f(x)是分式,则分母不为零;
(2)若f(x)是偶次根式,则被开方数大于或等于零;
(3)若函数y=(f(x))0,则f(x)≠0;
(4)若f(x)是由几个式子构成的,则函数的定义域要使各个式子都有意义;
(5)若f(x)是实际问题的解析式,则函数的定义域应使实际问题有意义.
解题归纳
训练题
1.
A
2.
D
<2>求抽象函数、复合函数的定义域
例4
求抽象函数或复合函数定义域的方法
(1)已知f(x)的定义域为A,求f(φ(x))的定义域,其实质是已知φ(x)的取值范围为A,求x的取值范围.
(2)已知f(φ(x))的定义域为B,求f(x)的定义域,其实质是已知f(φ(x))中x的取值范围为B,求φ(x)的取值范围(值域).
解题归纳
训练题
1.
2.
C
C
求抽象函数或复合函数的定义域时需明确的三个问题
(1)函数f(x)的定义域是指x的取值所成的集合.
(2)函数f(φ(x))的定义域是指x的取值范围,而不是φ(x)的取值范围.
(3)f(t),f(φ(x)),f(h(x))三个函数中的t,φ(x),h(x)在对应关系f下的取值范围相同.
解题归纳
<3>已知函数的定义域求参数
例5
训练题
1.
2.
D
(3,+∞)
<4>应用问题中的定义域
例6
如图所示,用长为1的铁丝围成下边为矩形、上边为半圆形的框架,若半圆的半径为,求此框架围成的面积与的函数解析式,并写出它的定义域.
训练题
D
三 函数求值或函数的值域问题
<1>函数求值问题
例7
[2020·黑龙江大庆实验中学高二检测] 若f(x)=x2-2x,则f(f(f(1)))=( )
A.1 B.2 C.3 D.4
【解题提示】 依次把自变量代入函数关系式,由内向外求值即可.
【解析】 由f(x)=x2-2x,可得f(1)=1-2=-1,所以f(f(1))=f(-1)=1+2=3,f(f(f(1)))=f(3)=9-6=3.
【答案】 C
训练题
15
A
<2>函数的值域问题
例8
例9
求函数值域的方法
求函数值域的常用方法:观察法、配方法、分离常数法、换元法、判别式法、反表示法、中间变量法.
(1)观察法:通过对函数解析式的简单变形,利用熟知的基本函数的值域,或利用函数图象的“最高点”和“最低点”观察函数的值域.如函数y=的值域为{y|0
解题归纳
(3)分离常数法:形如y=(ac≠ 0,ad≠bc)的函数常用分离常数法求值域.转化过程为y= =+ ,其结论是.
(4)换元法:形如y=ax+b+(a≠0)的函数常用换元法求值域,即先令t= ,求出x,并注明t的取值范围,再代入上式将y表示成关于t的二次函数,最后用配方法求值域.
注意:分离常数法的目的是将分式函数变为反比例型函数,换元法的目的是将函数变为二次函数,即将函数解析式变为熟悉的简单函数类型求值域.
解题归纳
(5)判别式法:形如y=(a,d中至少有一个不为零)的值域,常把函数转化成关于x的二次方程F(x,y)=0,通过方程有实根,判别式Δ≥0,求出y的取值范围.
(6)反表示法:根据函数解析式反解出x,根据x的取值范围转化为关于y的不等式求解.
(7)中间变量法:根据函数解析式确定一个已知范围的中间变量(如x2),用y表示出该中间变量,根据中间变量的取值范围转化为关于y的不等式求解.
解题归纳
训练题
{ f(x)| f(x)≠1}
<3>已知值域求参数
例9
已知函数值域求参数的解题提示
(1)注意调整思维方向,根据值域的含义将参数问题转化为方程的解或不等式的解集问题.
(2)根据方程的解或不等式的解集情况来确定参数的值或取值范围.
解题归纳
训练题
D
[2020·四川阆中中学高一检测] 函数f (x)=x2-4x-6的定义域为[0,m],值域为[-10,-6],则m的取值范围是( )
A.[0,4] B.[4,6] C.[2,6] D.[2,4]
四 对应关系问题
例10
实验测得音速与气温的一些数据如下表所示:
气温x/℃ 0 5 10 15 20
音速y/(米/秒) 331 334 337 340 343
(1)根据表内数据作图,由图可看出变量 随 的变化而变化.
(2)用x表示y的关系式为 .
(3)气温为22 ℃时,某人看到烟花燃放5秒后才听到声响,那么此人与燃放的烟花所在地相距约 米.
在一次百米赛跑中,甲、乙两人的路程与时间的关系如图所示,那么可以知道:
(1)甲、乙两人中先到达终点的是 .
(2)乙在这次赛跑中的速度为 m/s.
训练题
甲
8
小结
函数的概念
理解函数的概念需注意:
(1)A,B必须为非空数集,定义域或值域为空集的函数是不存在的.
(2)两个非空数集间的对应关系能否构成函数,主要看是否满足“三性”:任意性、存在性、唯一性.这是因为函数概念中明确要求对于非空数集A中的任意一个(任意性)元素x,在非空数集B中都有(存在性)唯一(唯一性)的元素y与之对应.这“三性”只要有一个不满足便不能构成函数.
(3)集合A是函数的定义域,因为给定A中每一个x值都有唯一的y值与之对应;集合B不一定是函数的值域,因为B中的元素可以没有与之对应者,即{f(x)|x∈A}B.
(4)在函数定义中,我们用符号y=f(x)表示函数,而不是“f乘x”.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
