人教版数学七年级下册 第九章不等式与不等式组章末复习 课件(共34张PPT)
文档属性
| 名称 | 人教版数学七年级下册 第九章不等式与不等式组章末复习 课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 394.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-06 14:15:03 | ||
图片预览









文档简介
(共34张PPT)
第九章 不等式与不等式组
章末复习
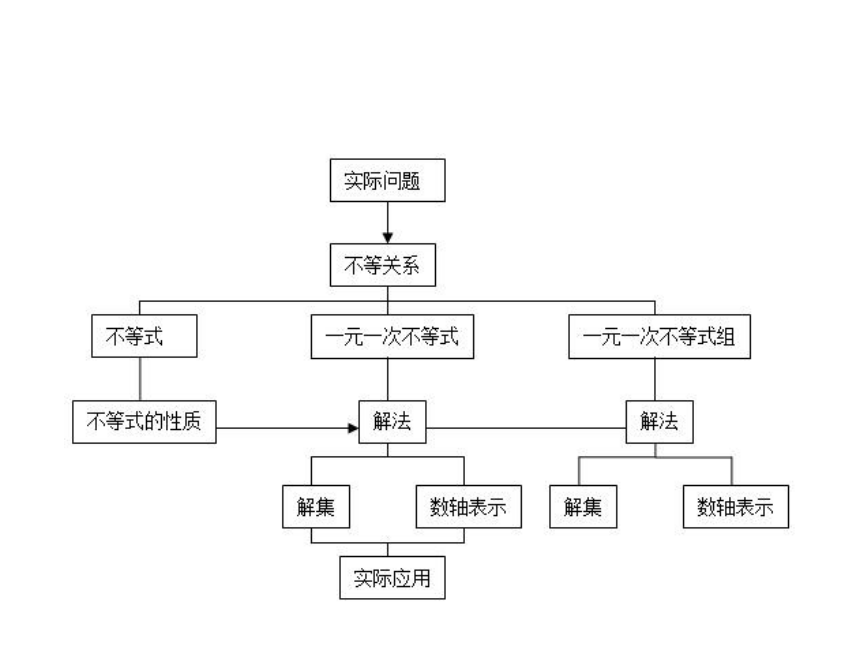
学习目标
1.构建不等式(组)知识间的联系,形成知识体系,并解决有关问题.
2.构建不等式的知识体系,解决有关问题.
不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.
不等式的性质是什么?
一元一次不等式的概念含几个要点:
(1)用不等号连接;
(2)不等号两边都是关于未知数的整式;
(3)只含有一个未知数,且含有未知数的项的最高
次数为1.
知识复习
易错点
去分母
去括号
移项
合并同类项
系数化为1
1、漏乘
2、分子式多项式去分母要加括号
1、括号外面是负数,变号
1、变号移项
1、注意是系数相加
1、注意不等号方向是否改变
2、分子、分母不要写反
不等式组的解集确定方法除利用数轴直观确定外,还可以用口诀确定:
同大取大,同小取小,
大小小大中间找,
大大小小没得找.
不等式的应用情况很多,但解所有的题目关键在于找准表示不等关系的语句,并能够列出不等式,再利用不等式的性质解不等式,这样问题才能得以解决.
当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属于通过列不等式(组)来解决的问题,而不属于通过列方程(组)来解决的问题.
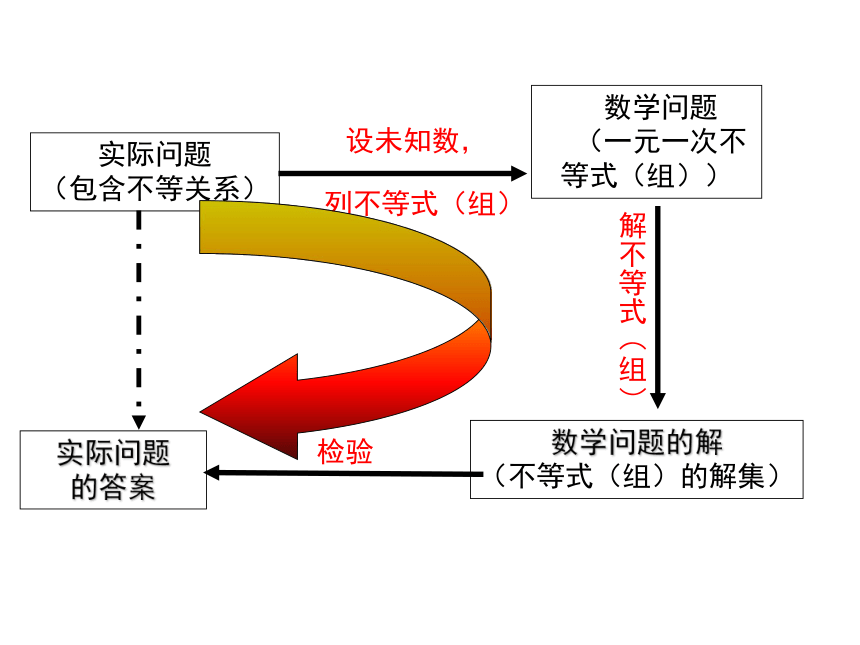
数学问题的解
(不等式(组)的解集)
实际问题
(包含不等关系)
设未知数,
列不等式(组)
数学问题
(一元一次不等式(组))
解不等式(组)
检验
实际问题
的答案
例1、 如果 ,那么下列不等式中不成立的是( )
(A)
(B)
(C)
(D)
B
分析:运用不等式的性质.
判断下列式子哪些是不等式?
(1) 3>2 (2) a2+1>0 (3) 3x2+2x
(4) x<2x+1 (5) x=2x-5
(6)x2+4x<3x+1 (7)a+b≠c
自己举出几个不等式的例子(至少两个)
是
是
是
是
是
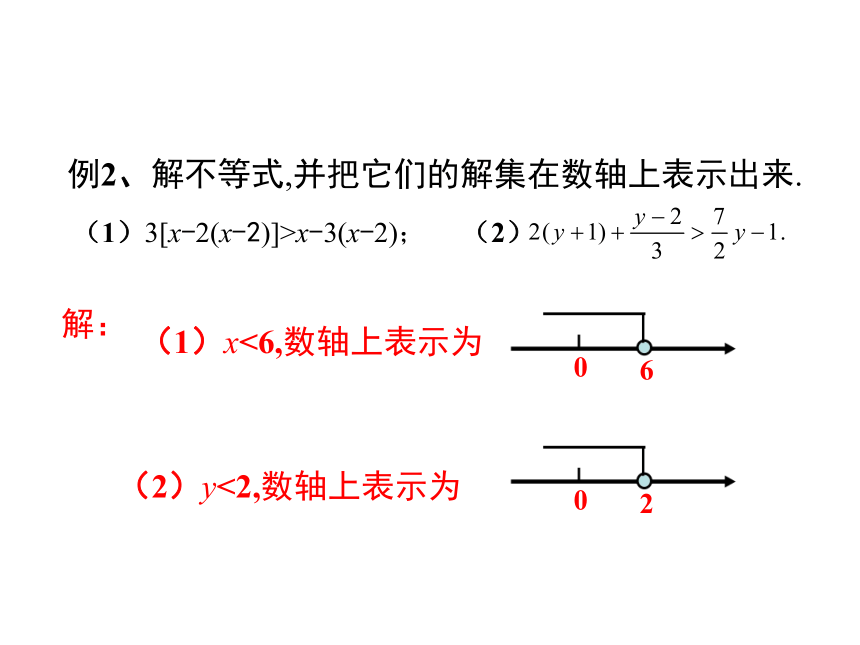
例2、解不等式,并把它们的解集在数轴上表示出来.
(1)3[x-2(x-2)]>x-3(x-2);
(2)
解:
(1)x<6,数轴上表示为
0
6
(2)y<2,数轴上表示为
0
2
若关于x的一元一次方程x-m+2=0的解是负数,则m的取值范围是( )
A、m≥2 B、m>2
C、m<2 D、m≤2
C
例3、解不等式组:
由不等式①得: x≤8
由不等式②得: x≥5
∴ 原不等式组的解集为:5≤x≤8
解:
0
1
2
-1
3
4
5
6
7
8
已知不等式组 有解,则a的取值范围为
( )
A.a>-2 B.a≥-2 C.a<2 D.a≥2
C
提示:解不等式x-a≥0,得x≥a;解不等式-2x>-4,得x<2.因为不等式组有解,故2在a的右边,即a<2.
例4、小明上午8时20分出发去郊游,10时20分时,小亮乘车从同一地点出发,已知小明每小时走4千米,那么小亮要在11时追上或超过小明,速度至少应是多少?
【分析】从路程下手找不等关系:
即小亮40分钟行进路程≥小明从8时20分到11时行进路程.
解:设小亮的速度为x千米/时,40分= 小时,
列不等式,得 ,解得x≥16.
答:小亮的速度至少为16千米/时.
例5、一堆玩具分给若干个小朋友,若每人分3件,则剩余4件;若前面每人分4件,则最后一人得到的玩具不足3件,求小朋友的人数与玩具数。
解:
设小朋友总共有x人,由此可得不等式组
3x+4-4(x-1)≥0,
3x+4-4(x-1)<3;
由此可得5所以x=6,7,8.
答:小朋友有6人,玩具有22件;或小朋友有7人,玩具有25件;或小朋友有8人,玩具有28件.
分析:
这是一个追赶问题,从路程下手找不等关系.小明出发时,小亮行了10:20-8:20=2小时.小明要在11点前追上小华 小亮行了2+ 小时,而小明行了 小时.
解:设小明的速度至少要每小时行x千米.
答:小亮的速度至少为16千米/时.
小明上午8时20分出发去郊游.10时20分时,小亮乘车出发.已知小明每小时走4 km,那么小亮要在11时前追上小明,速度至少应是多少?
课后训练
1.已知点M(3a-9,1-a)在第三象限,且它的横、纵坐标都是整数,则a的值是( )
A. 1 B. 2 C. 3 D. 0
2.关于x的不等式x-2a≤1的解集如图所示,则a的值是 .
-1
0
1
B
-1
基础检测
3、由 a>b 得 am2>bm2 的条件是( )
m>0
B. m<0
C. m≠0
D. m是任意有理数
C
4.点A( , )在第三象限,则m的取值范围是 ( )
A. B. C. D.
C
5.已知不等式组 有解,则a的取值范围为___
(A)a>-2 (B)a≥-2
(C)a<2 (D)a≥2 .
C
7.解不等式组: ,并把解集在数轴上表
示出来.
6.解不等式
解:x ≤8
解:18、解不等式组:
①
②
解:①不等式组的解集是 ;
②不等式组的解集是x≥9.
C
章末检测
C
D
A
B
1,2,3
1<x<2
1.3
第九章 不等式与不等式组
章末复习
学习目标
1.构建不等式(组)知识间的联系,形成知识体系,并解决有关问题.
2.构建不等式的知识体系,解决有关问题.
不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.
不等式的性质是什么?
一元一次不等式的概念含几个要点:
(1)用不等号连接;
(2)不等号两边都是关于未知数的整式;
(3)只含有一个未知数,且含有未知数的项的最高
次数为1.
知识复习
易错点
去分母
去括号
移项
合并同类项
系数化为1
1、漏乘
2、分子式多项式去分母要加括号
1、括号外面是负数,变号
1、变号移项
1、注意是系数相加
1、注意不等号方向是否改变
2、分子、分母不要写反
不等式组的解集确定方法除利用数轴直观确定外,还可以用口诀确定:
同大取大,同小取小,
大小小大中间找,
大大小小没得找.
不等式的应用情况很多,但解所有的题目关键在于找准表示不等关系的语句,并能够列出不等式,再利用不等式的性质解不等式,这样问题才能得以解决.
当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属于通过列不等式(组)来解决的问题,而不属于通过列方程(组)来解决的问题.
数学问题的解
(不等式(组)的解集)
实际问题
(包含不等关系)
设未知数,
列不等式(组)
数学问题
(一元一次不等式(组))
解不等式(组)
检验
实际问题
的答案
例1、 如果 ,那么下列不等式中不成立的是( )
(A)
(B)
(C)
(D)
B
分析:运用不等式的性质.
判断下列式子哪些是不等式?
(1) 3>2 (2) a2+1>0 (3) 3x2+2x
(4) x<2x+1 (5) x=2x-5
(6)x2+4x<3x+1 (7)a+b≠c
自己举出几个不等式的例子(至少两个)
是
是
是
是
是
例2、解不等式,并把它们的解集在数轴上表示出来.
(1)3[x-2(x-2)]>x-3(x-2);
(2)
解:
(1)x<6,数轴上表示为
0
6
(2)y<2,数轴上表示为
0
2
若关于x的一元一次方程x-m+2=0的解是负数,则m的取值范围是( )
A、m≥2 B、m>2
C、m<2 D、m≤2
C
例3、解不等式组:
由不等式①得: x≤8
由不等式②得: x≥5
∴ 原不等式组的解集为:5≤x≤8
解:
0
1
2
-1
3
4
5
6
7
8
已知不等式组 有解,则a的取值范围为
( )
A.a>-2 B.a≥-2 C.a<2 D.a≥2
C
提示:解不等式x-a≥0,得x≥a;解不等式-2x>-4,得x<2.因为不等式组有解,故2在a的右边,即a<2.
例4、小明上午8时20分出发去郊游,10时20分时,小亮乘车从同一地点出发,已知小明每小时走4千米,那么小亮要在11时追上或超过小明,速度至少应是多少?
【分析】从路程下手找不等关系:
即小亮40分钟行进路程≥小明从8时20分到11时行进路程.
解:设小亮的速度为x千米/时,40分= 小时,
列不等式,得 ,解得x≥16.
答:小亮的速度至少为16千米/时.
例5、一堆玩具分给若干个小朋友,若每人分3件,则剩余4件;若前面每人分4件,则最后一人得到的玩具不足3件,求小朋友的人数与玩具数。
解:
设小朋友总共有x人,由此可得不等式组
3x+4-4(x-1)≥0,
3x+4-4(x-1)<3;
由此可得5
答:小朋友有6人,玩具有22件;或小朋友有7人,玩具有25件;或小朋友有8人,玩具有28件.
分析:
这是一个追赶问题,从路程下手找不等关系.小明出发时,小亮行了10:20-8:20=2小时.小明要在11点前追上小华 小亮行了2+ 小时,而小明行了 小时.
解:设小明的速度至少要每小时行x千米.
答:小亮的速度至少为16千米/时.
小明上午8时20分出发去郊游.10时20分时,小亮乘车出发.已知小明每小时走4 km,那么小亮要在11时前追上小明,速度至少应是多少?
课后训练
1.已知点M(3a-9,1-a)在第三象限,且它的横、纵坐标都是整数,则a的值是( )
A. 1 B. 2 C. 3 D. 0
2.关于x的不等式x-2a≤1的解集如图所示,则a的值是 .
-1
0
1
B
-1
基础检测
3、由 a>b 得 am2>bm2 的条件是( )
m>0
B. m<0
C. m≠0
D. m是任意有理数
C
4.点A( , )在第三象限,则m的取值范围是 ( )
A. B. C. D.
C
5.已知不等式组 有解,则a的取值范围为___
(A)a>-2 (B)a≥-2
(C)a<2 (D)a≥2 .
C
7.解不等式组: ,并把解集在数轴上表
示出来.
6.解不等式
解:x ≤8
解:1
①
②
解:①不等式组的解集是 ;
②不等式组的解集是x≥9.
C
章末检测
C
D
A
B
1,2,3
1<x<2
1.3
