信息学奥林匹克禁赛(入门)——归并排序算法精讲课件(24张PPT)
文档属性
| 名称 | 信息学奥林匹克禁赛(入门)——归并排序算法精讲课件(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-04-05 18:18:14 | ||
图片预览





文档简介
(共24张PPT)
排序算法——归并排序
信息学奥林匹克竞赛(入门)【高中】
排序算法——归并排序
Content
归并排序算法精讲
经典例题讲解
排序算法——归并排序
-Content
排序算法——归并排序
归并排序算法精讲
排序算法——归并排序
排序算法——归并排序
排序算法——归并排序
-归并排序算法精讲
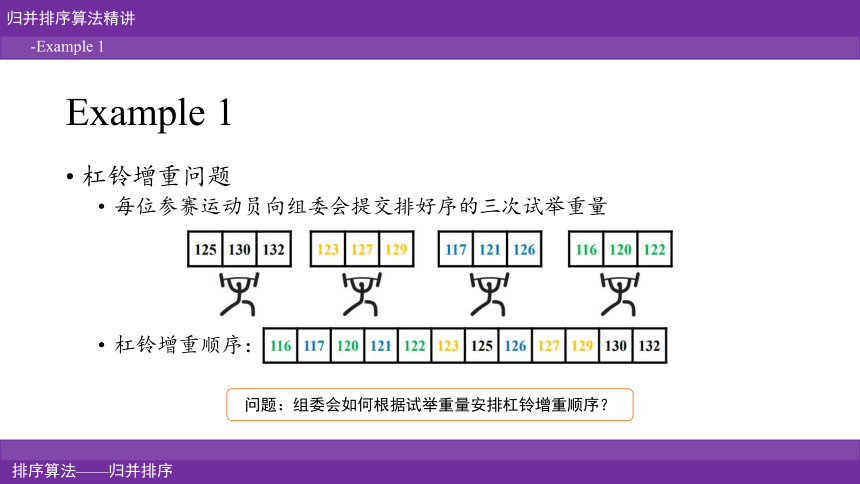
Example 1
杠铃增重问题
每位参赛运动员向组委会提交排好序的三次试举重量
杠铃增重顺序:
问题:组委会如何根据试举重量安排杠铃增重顺序?
排序算法——归并排序
-Example 1
归并排序算法精讲
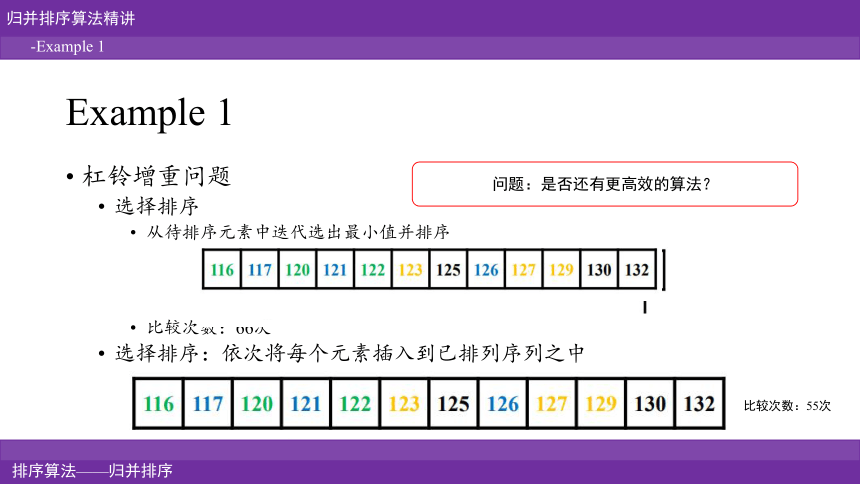
Example 1
杠铃增重问题
选择排序
从待排序元素中迭代选出最小值并排序
比较次数:66次
选择排序:依次将每个元素插入到已排列序列之中
比较次数:55次
问题:是否还有更高效的算法?
排序算法——归并排序
-Example 1
归并排序算法精讲
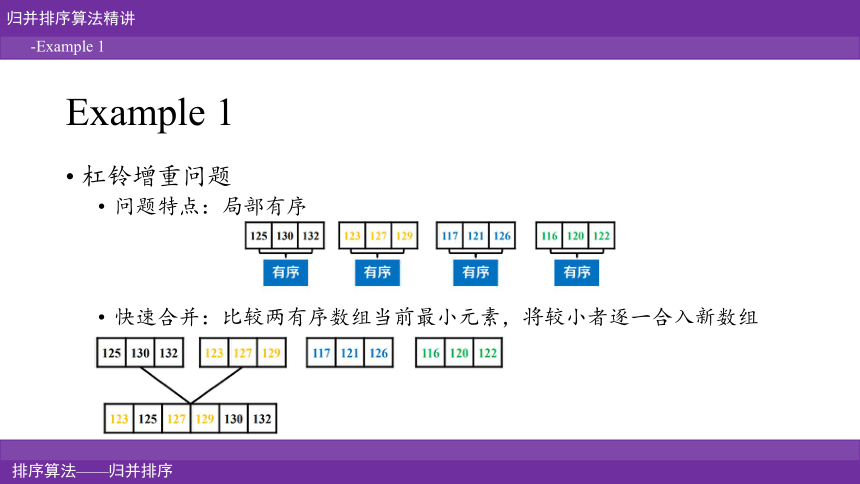
Example 1
杠铃增重问题
问题特点:局部有序
快速合并:比较两有序数组当前最小元素,将较小者逐一合入新数组
排序算法——归并排序
-Example 1
归并排序算法精讲
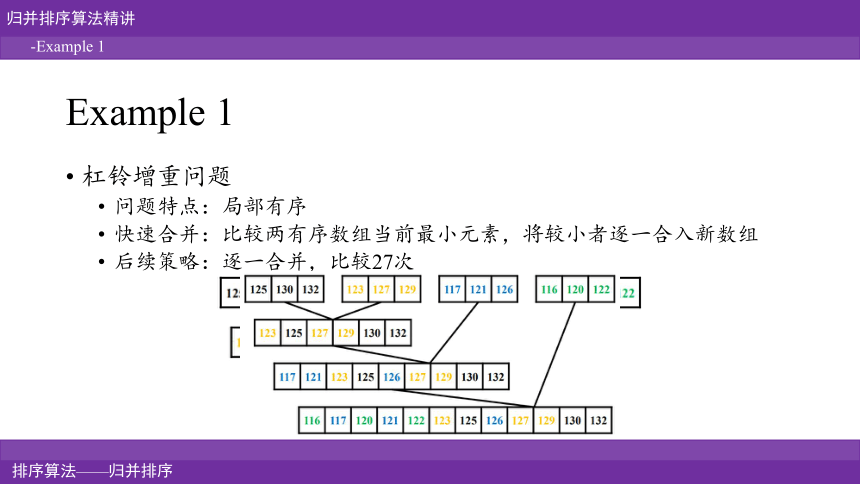
Example 1
杠铃增重问题
问题特点:局部有序
快速合并:比较两有序数组当前最小元素,将较小者逐一合入新数组
后续策略:逐一合并,比较27次
排序算法——归并排序
-Example 1
归并排序算法精讲
Example 1
杠铃增重问题
问题特点:局部有序
快速合并:比较两有序数组当前最小元素,将较小者逐一合入新数组
后续策略:
逐一合并,比较27次
两两合并:比较24次
策略名称 4位选手 8位选手 16位选手
逐一合并 27次 105次 405次
两两合并 24次 72次 192次
求解杠铃增重问题的两两合并策略对排序问题有何启发?
排序算法——归并排序
-Example 1
归并排序算法精讲
归并排序
定义:归并排序是建立在归并操作上的一种有效,稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列。
历史:1945年,冯 诺依曼提出归并排序。
算法流程:
将数组排序问题分解为和排序问题
递归解决子问题得到两个有序的子数组
将两个有序子数组合并为一个有序数组
排序算法——归并排序
归并排序算法精讲
-归并排序
归并排序
分解原问题
解决子问题
合并问题解
原问题分解为多个子问题
递归求解各个子问题
将结果合并为原问题解
归并排序:
分解数组,
递归求解,
合并排序
排序算法——归并排序
归并排序算法精讲
-归并排序
归并排序
程序复杂度:
分析方法:递归树法
框架:
排序算法——归并排序
归并排序算法精讲
-归并排序
Example 2
对以下数组进行排列:
下面我们运用归并排序算法对此数组进行排序
i 0 1 2 3 4
a[i] 19 15 37 12 25
排序算法——归并排序
归并排序算法精讲
-Example 2
第一步:分解
首先将数组分解成两部分,即19、15、37为一组,12、25为一组,为了区分,我们起个名字叫“第一层”,如下:
19 15 37
12 25
排序算法——归并排序
归并排序算法精讲
-Example 2
第二步:分解
继续分解,19、15为一组,37为一组,12为一组,25为一组,这四组为“第二层”,如下:
19 15
25
37
12
排序算法——归并排序
归并排序算法精讲
-Example 2
第三步:分解
继续分解,此时只剩下19、15这一组可以分解,分解成19、15,这两组为“第三层”,如下:
15
19
排序算法——归并排序
归并排序算法精讲
-Example 2
第四步:归并
由于所有组都已经分解成只有1个元素,开始进行归并,从“高层”开始归并,即先归并“第三层”,比较“第三层”两组元素,19 < 15,因此将15排在19前面,由于已经没有元素,结束此次归并,如下:
19 15
排序算法——归并排序
归并排序算法精讲
-Example 2
第五步:归并
继续归并,此次归并“第二层”,这一层有4个组,进行两两比较。首先,比较15、19和37:15 < 37,所以15放第一个位置,接着比较19和37,19 < 37,所以19放第二个位置,此时第一组15、19已经没有元素,于是将37填入15和19之后。接着比较:12和25:12 < 25,所以12放第一个位置,由于第一组12已经没有元素,于是将25填入12之后。归并的结果如下:
15 19 37
12 25
排序算法——归并排序
归并排序算法精讲
-Example 2
第六步:归并
继续归并,此次归并“第一层”,这一组有2个组,第一组:15、19、37,第二组:12、25。同样的,取两组的第1个数比较:15 > 12,所以12放第1个位置;接着取第二组的第2个数比较:15 < 25,所以15放第2个位置;接着取第一组的第2个数比较:19 < 25,所以19放第3个位置;接着取第一组的第3个数比较:37 > 25,所以25放第4个位置;由于第二组已经没有元素,所以37自然归入第5个位置。此时,归并结束,最终数组如下:
12 15 19 25 37
排序算法——归并排序
归并排序算法精讲
-Example 2
完整过程
排序算法——归并排序
归并排序算法精讲
-Example 2
动画演示
排序算法——归并排序
归并排序算法精讲
-Example 2
经典例题讲解
排序算法——归并排序
排序算法——归并排序
排序算法——归并排序
-经典例题讲解
【NOIP1998提高组】拼数
题目描述:
设有n个正整数,然后将它们联接成一排,相邻数字首尾相接,组成一个最大的整数。
输入格式:
第一行有一个整数,表示数字个数n。
第二行有n个整数,表示给出的n个整数。
输出格式:
一个正整数,表示最大的整数
排序算法——归并排序
经典例题讲解
-Problem 1
求第 k小的数
题目描述:
输入n(且n为奇数)个数字 ,输出这些数字的第k小的数。最小的数是第0小。
输入格式:
第一行有一个整数,表示数字个数n。
第二行有n个整数,表示给出的n个整数。
输出格式:
一个正整数,表示第k小的数.
排序算法——归并排序
经典例题讲解
-Problem 2
Thanks For Listening!
排序算法——归并排序
排序算法——归并排序
排序算法——归并排序
信息学奥林匹克竞赛(入门)【高中】
排序算法——归并排序
Content
归并排序算法精讲
经典例题讲解
排序算法——归并排序
-Content
排序算法——归并排序
归并排序算法精讲
排序算法——归并排序
排序算法——归并排序
排序算法——归并排序
-归并排序算法精讲
Example 1
杠铃增重问题
每位参赛运动员向组委会提交排好序的三次试举重量
杠铃增重顺序:
问题:组委会如何根据试举重量安排杠铃增重顺序?
排序算法——归并排序
-Example 1
归并排序算法精讲
Example 1
杠铃增重问题
选择排序
从待排序元素中迭代选出最小值并排序
比较次数:66次
选择排序:依次将每个元素插入到已排列序列之中
比较次数:55次
问题:是否还有更高效的算法?
排序算法——归并排序
-Example 1
归并排序算法精讲
Example 1
杠铃增重问题
问题特点:局部有序
快速合并:比较两有序数组当前最小元素,将较小者逐一合入新数组
排序算法——归并排序
-Example 1
归并排序算法精讲
Example 1
杠铃增重问题
问题特点:局部有序
快速合并:比较两有序数组当前最小元素,将较小者逐一合入新数组
后续策略:逐一合并,比较27次
排序算法——归并排序
-Example 1
归并排序算法精讲
Example 1
杠铃增重问题
问题特点:局部有序
快速合并:比较两有序数组当前最小元素,将较小者逐一合入新数组
后续策略:
逐一合并,比较27次
两两合并:比较24次
策略名称 4位选手 8位选手 16位选手
逐一合并 27次 105次 405次
两两合并 24次 72次 192次
求解杠铃增重问题的两两合并策略对排序问题有何启发?
排序算法——归并排序
-Example 1
归并排序算法精讲
归并排序
定义:归并排序是建立在归并操作上的一种有效,稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列。
历史:1945年,冯 诺依曼提出归并排序。
算法流程:
将数组排序问题分解为和排序问题
递归解决子问题得到两个有序的子数组
将两个有序子数组合并为一个有序数组
排序算法——归并排序
归并排序算法精讲
-归并排序
归并排序
分解原问题
解决子问题
合并问题解
原问题分解为多个子问题
递归求解各个子问题
将结果合并为原问题解
归并排序:
分解数组,
递归求解,
合并排序
排序算法——归并排序
归并排序算法精讲
-归并排序
归并排序
程序复杂度:
分析方法:递归树法
框架:
排序算法——归并排序
归并排序算法精讲
-归并排序
Example 2
对以下数组进行排列:
下面我们运用归并排序算法对此数组进行排序
i 0 1 2 3 4
a[i] 19 15 37 12 25
排序算法——归并排序
归并排序算法精讲
-Example 2
第一步:分解
首先将数组分解成两部分,即19、15、37为一组,12、25为一组,为了区分,我们起个名字叫“第一层”,如下:
19 15 37
12 25
排序算法——归并排序
归并排序算法精讲
-Example 2
第二步:分解
继续分解,19、15为一组,37为一组,12为一组,25为一组,这四组为“第二层”,如下:
19 15
25
37
12
排序算法——归并排序
归并排序算法精讲
-Example 2
第三步:分解
继续分解,此时只剩下19、15这一组可以分解,分解成19、15,这两组为“第三层”,如下:
15
19
排序算法——归并排序
归并排序算法精讲
-Example 2
第四步:归并
由于所有组都已经分解成只有1个元素,开始进行归并,从“高层”开始归并,即先归并“第三层”,比较“第三层”两组元素,19 < 15,因此将15排在19前面,由于已经没有元素,结束此次归并,如下:
19 15
排序算法——归并排序
归并排序算法精讲
-Example 2
第五步:归并
继续归并,此次归并“第二层”,这一层有4个组,进行两两比较。首先,比较15、19和37:15 < 37,所以15放第一个位置,接着比较19和37,19 < 37,所以19放第二个位置,此时第一组15、19已经没有元素,于是将37填入15和19之后。接着比较:12和25:12 < 25,所以12放第一个位置,由于第一组12已经没有元素,于是将25填入12之后。归并的结果如下:
15 19 37
12 25
排序算法——归并排序
归并排序算法精讲
-Example 2
第六步:归并
继续归并,此次归并“第一层”,这一组有2个组,第一组:15、19、37,第二组:12、25。同样的,取两组的第1个数比较:15 > 12,所以12放第1个位置;接着取第二组的第2个数比较:15 < 25,所以15放第2个位置;接着取第一组的第2个数比较:19 < 25,所以19放第3个位置;接着取第一组的第3个数比较:37 > 25,所以25放第4个位置;由于第二组已经没有元素,所以37自然归入第5个位置。此时,归并结束,最终数组如下:
12 15 19 25 37
排序算法——归并排序
归并排序算法精讲
-Example 2
完整过程
排序算法——归并排序
归并排序算法精讲
-Example 2
动画演示
排序算法——归并排序
归并排序算法精讲
-Example 2
经典例题讲解
排序算法——归并排序
排序算法——归并排序
排序算法——归并排序
-经典例题讲解
【NOIP1998提高组】拼数
题目描述:
设有n个正整数,然后将它们联接成一排,相邻数字首尾相接,组成一个最大的整数。
输入格式:
第一行有一个整数,表示数字个数n。
第二行有n个整数,表示给出的n个整数。
输出格式:
一个正整数,表示最大的整数
排序算法——归并排序
经典例题讲解
-Problem 1
求第 k小的数
题目描述:
输入n(且n为奇数)个数字 ,输出这些数字的第k小的数。最小的数是第0小。
输入格式:
第一行有一个整数,表示数字个数n。
第二行有n个整数,表示给出的n个整数。
输出格式:
一个正整数,表示第k小的数.
排序算法——归并排序
经典例题讲解
-Problem 2
Thanks For Listening!
排序算法——归并排序
排序算法——归并排序
同课章节目录
