2.3.2 平面与平面垂直的判定
图片预览





文档简介
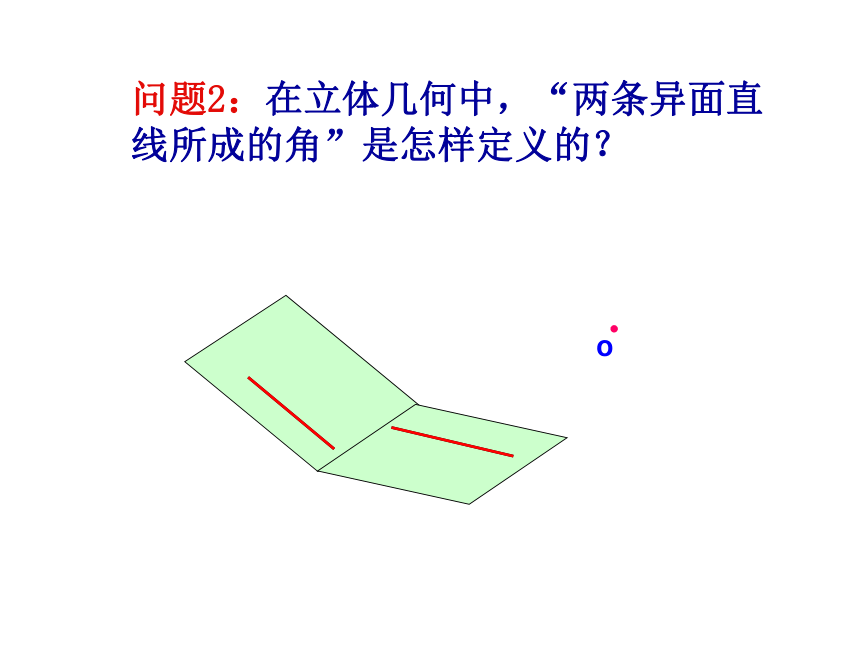
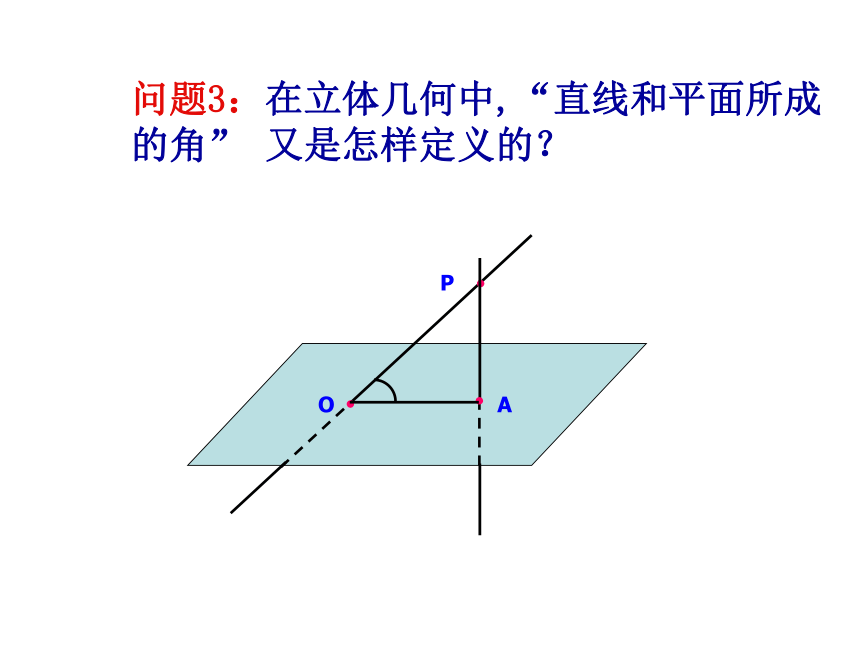
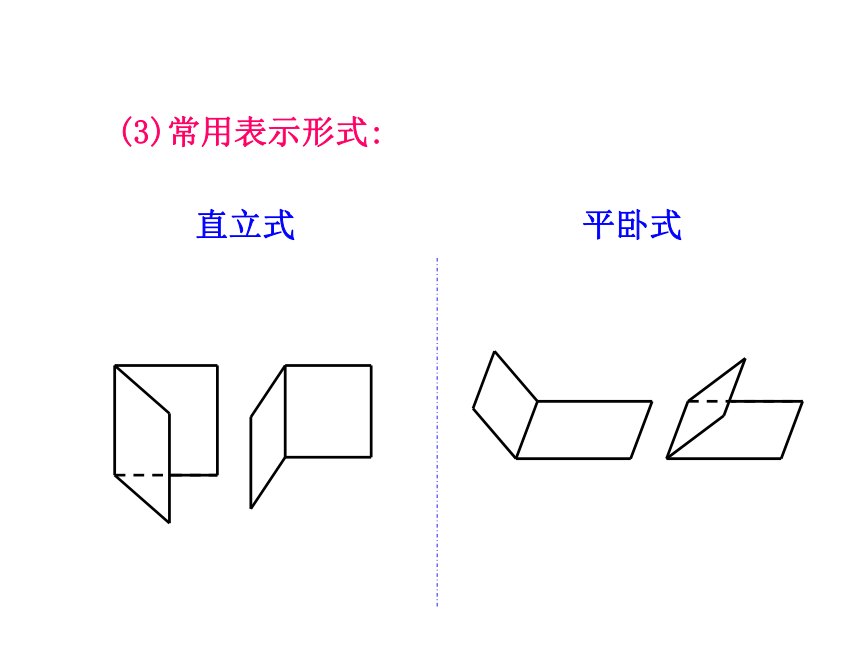
课件28张PPT。2.3.2 平面与平面垂直的判定(1)(一)温故知新问题1:平面几何中“角”是怎样定义的?从平面内一点出发的两条射线所组成的图形叫做角.AB问题2:在立体几何中,“两条异面直线所成的角”是怎样定义的??OP?A问题3:在立体几何中,“直线和平面所成的角” 又是怎样定义的?资料一:沙发资料二:室内一景资料三:水库一角.(二)探索研究平面内的一条直线把平面分为两部分,其中的每一部分都叫做一个半平面。(1)半平面:从一条直线出发的两个半平面所组成的图形叫做二面角。(2)二面角:1、二面角的有关概念(3)常用表示形式:直立式平卧式2、二面角的记法表示从平面内一点出发的两条射线(半直线)所组成的图形从空间一直线出发的两个半平面所组成的图形射线—点(顶点)—射线半平面—线(棱)—半平面∠AOB二面角α-l -β或α-AB-β3、二面角的度量 ① “把门开大一些”,是指哪个角大一些呢?
② 我们应如何度量二两角的大小呢? 以二面角的棱上任意一点为端点,在两个平面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.(1)二面角平面角的定义(2)二面角平面角的作法①定义法:垂直于二面角棱的任一平面与两个半平面的交线所成的角是二面角的平面角。②垂面法:(3)找二面角的平面角时要注意:②在找二面角的平面角时,要求 “OA⊥l” ,
OB⊥l;①∠AOB的大小与点O在l上位置无关;③二面角平面角的范围 [0°,180°]①直二面角的定义:两个平面相交,如果它们所成的二面角
是直二面角,就说这两个平面互相垂直.平面角是直角的二面角叫做直二面角.②两个平面互相垂直的定义:(4) 当二面角的平面角是直角时,这两个平面的位置关系怎样?记法:画法:α⊥β如何检测所砌的墙面和地面垂直?门面在转动过程中与地面是否垂直?平面与平面垂直的判定定理如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。简记为:线面垂直,面面垂直符号表示:例1: 设AB是圆O的直径,PA垂直于圆O所在平面,C是
圆周上不同于A、B的任意一点.
求证:平面PAC⊥平面PBC(三)知识应用证明:设⊙O所在平面为α,又∵ AB是⊙O的直径,
∴ BC⊥AC∵PA⊥α,BC α,
∴PA⊥BC又∵ PA∩AC=A,PA 平面PAC,AC 平面PAC
∴ BC⊥平面PAC又∵ BC 平面PBC,
∴平面PAC⊥平面PBC。如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,
∠ADC=45°,AD=AC=1,O为AC的中点,
PO⊥平面ABCD,PO=2,M为PD的中点.
(1)证明:PB∥平面ACM
(2)证明:平面PAD⊥平面PAC.(1)证明:
连接BD,MO.在平行四边形ABCD中,
因为O为AC的中点,所以O为BD的中点.
又M为PD的中点,
所以PB∥MO.
因为PB?平面ACM,MO?平面ACM,
所以PB∥平面ACM.
(2)证明:
因为∠ADC=45°,且AD=AC=1,
所以∠DAC=90°,即AD⊥AC.
又PO⊥平面ABCD,AD?平面ABCD,
所以PO⊥AD.
而AC∩PO=O,
所以AD⊥平面PAC.
又AD?平面PAD
所以平面PAD⊥平面PAC
(四)运用反馈探究:已知AB⊥平面BCD,BC⊥CD,你能发现哪些平面互相垂直,为什么?平面ABD⊥平面BCD平面ABC⊥平面BCD平面ACD⊥平面ABC(五)小结反思1.这节课主要学习哪些概念?2.两个平面垂直的判定定理的内容是什么?
它与直线与平面垂直的判定定理有何关系?线线垂直线面垂直面面垂直空间垂直关系之间的转化半平面 二面角 二面角的平面角
直二面角 两个平面互相垂直2.如果平面α内有一条直线垂直于平面β内的两
条直线,则α⊥β.( )(六)课堂练习1.如果平面α内有一条直线垂直于平面β内的一
条直线,则α⊥β.( )3. 如果平面α内的一条直线垂直于平面β内的两
条相交直线, 则α⊥β.( )
判断下列各题:××√√如图所示,三棱柱A1B1C1—ABC的三视图中,正(主)视图
和侧(左)视图是全等的矩形,俯视图是等腰直角三角形,
点M是A1B1的中点.
(1)求证:B1C∥平面AC1M;
(2)求证:平面AC1M⊥平面AA1B1B.课堂升华 (1)由三视图可知三棱柱A1B1C1—ABC为直三棱柱,
底面是等腰直角三角形,且∠ACB=90°.连结A1C,
设A1C∩AC1=O,连结MO,
由题意可知,A1O=CO,A1M=B1M,
∴MO∥B1C,
又MO?平面AC1M,
B1C?平面AC1M,∴B1C∥平面AC1M.
(2)∵A1C1=B1C1,M为A1B1的中点,
∴C1M⊥A1B1,
又平面A1B1C1⊥平面AA1B1B,
平面A1B1C1∩平面AA1B1B=A1B1,
∴C1M⊥平面AA1B1B,
又C1M?平面AC1M,
∴平面AC1M⊥平面AA1B1B.【证明】习题2.3
A组 第4题 B组 第1题(七)课后作业
② 我们应如何度量二两角的大小呢? 以二面角的棱上任意一点为端点,在两个平面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.(1)二面角平面角的定义(2)二面角平面角的作法①定义法:垂直于二面角棱的任一平面与两个半平面的交线所成的角是二面角的平面角。②垂面法:(3)找二面角的平面角时要注意:②在找二面角的平面角时,要求 “OA⊥l” ,
OB⊥l;①∠AOB的大小与点O在l上位置无关;③二面角平面角的范围 [0°,180°]①直二面角的定义:两个平面相交,如果它们所成的二面角
是直二面角,就说这两个平面互相垂直.平面角是直角的二面角叫做直二面角.②两个平面互相垂直的定义:(4) 当二面角的平面角是直角时,这两个平面的位置关系怎样?记法:画法:α⊥β如何检测所砌的墙面和地面垂直?门面在转动过程中与地面是否垂直?平面与平面垂直的判定定理如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。简记为:线面垂直,面面垂直符号表示:例1: 设AB是圆O的直径,PA垂直于圆O所在平面,C是
圆周上不同于A、B的任意一点.
求证:平面PAC⊥平面PBC(三)知识应用证明:设⊙O所在平面为α,又∵ AB是⊙O的直径,
∴ BC⊥AC∵PA⊥α,BC α,
∴PA⊥BC又∵ PA∩AC=A,PA 平面PAC,AC 平面PAC
∴ BC⊥平面PAC又∵ BC 平面PBC,
∴平面PAC⊥平面PBC。如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,
∠ADC=45°,AD=AC=1,O为AC的中点,
PO⊥平面ABCD,PO=2,M为PD的中点.
(1)证明:PB∥平面ACM
(2)证明:平面PAD⊥平面PAC.(1)证明:
连接BD,MO.在平行四边形ABCD中,
因为O为AC的中点,所以O为BD的中点.
又M为PD的中点,
所以PB∥MO.
因为PB?平面ACM,MO?平面ACM,
所以PB∥平面ACM.
(2)证明:
因为∠ADC=45°,且AD=AC=1,
所以∠DAC=90°,即AD⊥AC.
又PO⊥平面ABCD,AD?平面ABCD,
所以PO⊥AD.
而AC∩PO=O,
所以AD⊥平面PAC.
又AD?平面PAD
所以平面PAD⊥平面PAC
(四)运用反馈探究:已知AB⊥平面BCD,BC⊥CD,你能发现哪些平面互相垂直,为什么?平面ABD⊥平面BCD平面ABC⊥平面BCD平面ACD⊥平面ABC(五)小结反思1.这节课主要学习哪些概念?2.两个平面垂直的判定定理的内容是什么?
它与直线与平面垂直的判定定理有何关系?线线垂直线面垂直面面垂直空间垂直关系之间的转化半平面 二面角 二面角的平面角
直二面角 两个平面互相垂直2.如果平面α内有一条直线垂直于平面β内的两
条直线,则α⊥β.( )(六)课堂练习1.如果平面α内有一条直线垂直于平面β内的一
条直线,则α⊥β.( )3. 如果平面α内的一条直线垂直于平面β内的两
条相交直线, 则α⊥β.( )
判断下列各题:××√√如图所示,三棱柱A1B1C1—ABC的三视图中,正(主)视图
和侧(左)视图是全等的矩形,俯视图是等腰直角三角形,
点M是A1B1的中点.
(1)求证:B1C∥平面AC1M;
(2)求证:平面AC1M⊥平面AA1B1B.课堂升华 (1)由三视图可知三棱柱A1B1C1—ABC为直三棱柱,
底面是等腰直角三角形,且∠ACB=90°.连结A1C,
设A1C∩AC1=O,连结MO,
由题意可知,A1O=CO,A1M=B1M,
∴MO∥B1C,
又MO?平面AC1M,
B1C?平面AC1M,∴B1C∥平面AC1M.
(2)∵A1C1=B1C1,M为A1B1的中点,
∴C1M⊥A1B1,
又平面A1B1C1⊥平面AA1B1B,
平面A1B1C1∩平面AA1B1B=A1B1,
∴C1M⊥平面AA1B1B,
又C1M?平面AC1M,
∴平面AC1M⊥平面AA1B1B.【证明】习题2.3
A组 第4题 B组 第1题(七)课后作业
