高中数学 第一章 算法单元测试 新人教A版必修3
文档属性
| 名称 | 高中数学 第一章 算法单元测试 新人教A版必修3 |

|
|
| 格式 | zip | ||
| 文件大小 | 179.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-27 00:00:00 | ||
图片预览


文档简介
第一章 算法单元测试
一、选择题
1.下列给出的赋值语句中正确的是( )
A.6=a+5 B.M =-M C.6=a=b D.x-y=10
2.算法S1: m=a
S2: 若bS3: 若cS4: 若dS5: 输出m,则输出m表示 ( )
A.a,b,c,d中最大值 B.a,b,c,d中最小值
C.将a,b,c,d由小到大排序 D.将a,b,c,d由大到小排序
3.已知,,,,根据上述系列等式,可确定和和的最大公约数是( )
A.19 B.3 C.57 D.34
4.求满足的最小正整数,写出它的程序必须用( )
A.输入(出)语句 B.条件语句
C.“while”语句 D.“for”语句
5.以下给出计算的值的四个程序,其中正确的( )
A. B.
C. D.
6、将两个数a=25,b=9交换,使a=9,b=25,下面语句正确一组是 ( )
A B C D
7、条件语句的一般形式是“if A then B else C”,其中B表示的是 ( )
A、满足条件时执行的内容 B、条件语句 C、条件 D、不满足条件时执行的内容
8、for 语句的一般格式为:for i from a to b step c,其中a 的意义是 ( )
A、循环变量初始值 B、循环变量终值
C、循环体 D、循环条件的语句
9、右边程序运行的结果是 ( )
A、1,2,3 B、2,3,1 C、2,3,2 D、3,2,1
10、右边程序运行后的输出结果为 ( )
A、17 B、19 C、21 D、23
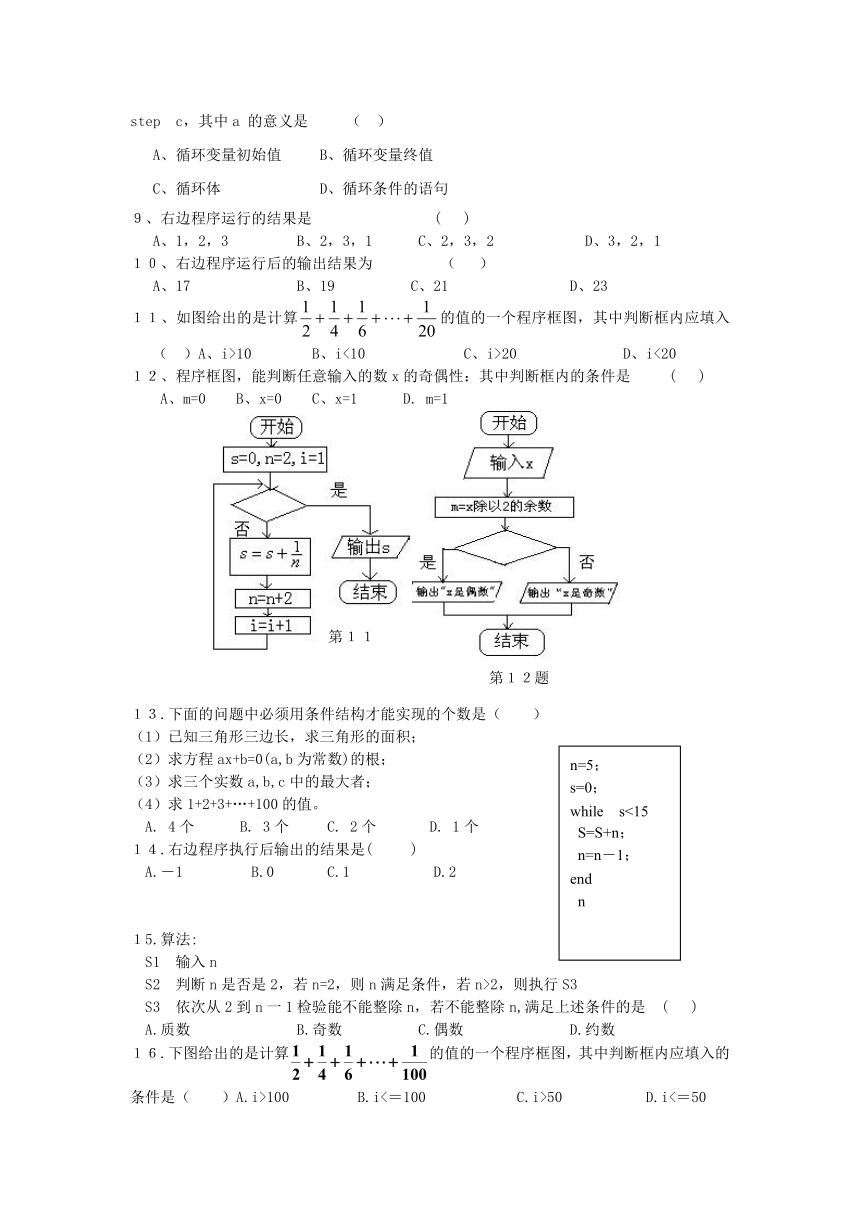
11、如图给出的是计算的值的一个程序框图,其中判断框内应填入 ( )A、i>10 B、i<10 C、i>20 D、i<20
12、程序框图,能判断任意输入的数x的奇偶性:其中判断框内的条件是 ( )
A、m=0 B、x=0 C、x=1 D. m=1
13.下面的问题中必须用条件结构才能实现的个数是( )
(1)已知三角形三边长,求三角形的面积;
(2)求方程ax+b=0(a,b为常数)的根;
(3)求三个实数a,b,c中的最大者;
(4)求1+2+3+…+100的值。
A. 4个 B. 3个 C. 2个 D. 1个
14.右边程序执行后输出的结果是( )
A.-1 B.0 C.1 D.2
15.算法:
S1 输入n
S2 判断n是否是2,若n=2,则n满足条件,若n>2,则执行S3
S3 依次从2到n一1检验能不能整除n,若不能整除n,满足上述条件的是 ( )
A.质数 B.奇数 C.偶数 D.约数
16.下图给出的是计算的值的一个程序框图,其中判断框内应填入的条件是( )A.i>100 B.i<=100 C.i>50 D.i<=50
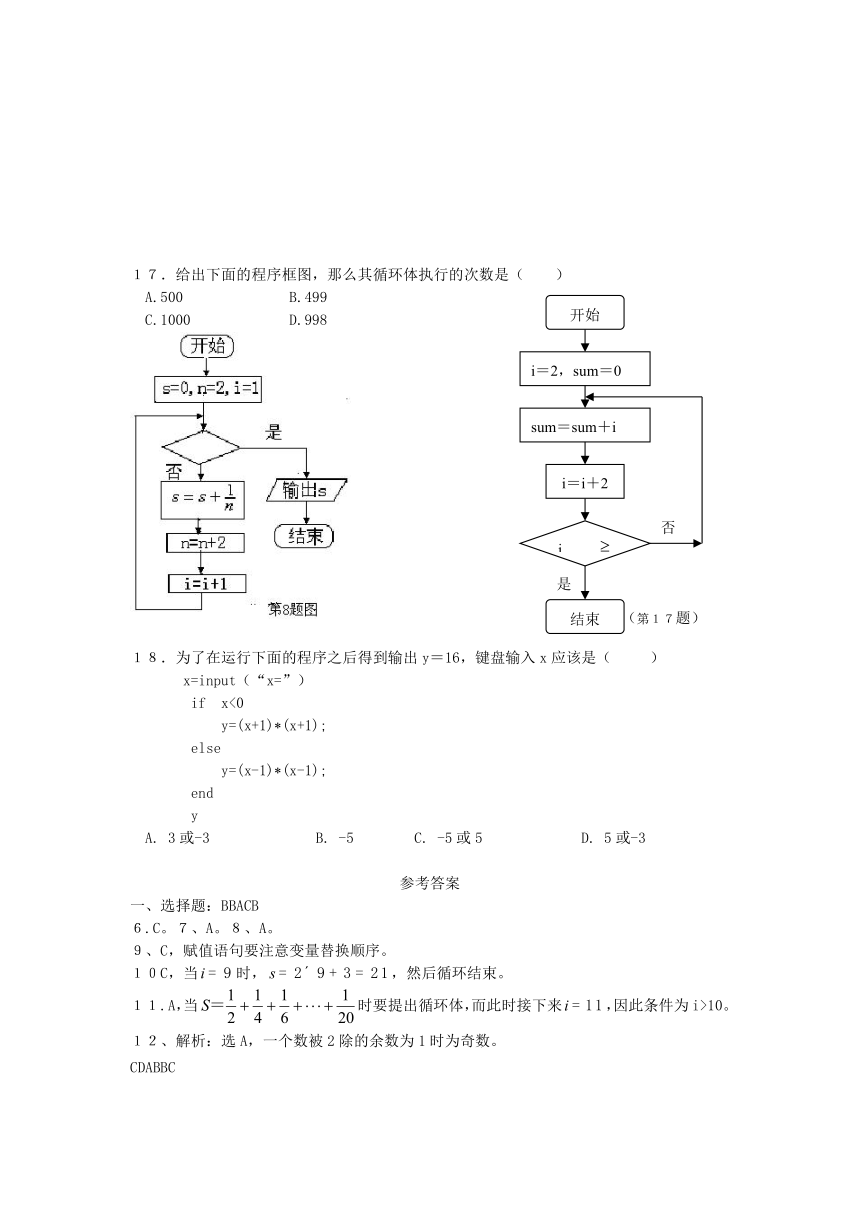
17.给出下面的程序框图,那么其循环体执行的次数是( )
A.500 B.499
C.1000 D.998
18.为了在运行下面的程序之后得到输出y=16,键盘输入x应该是( )
x=input(“x=”)
if x<0
y=(x+1)((x+1);
else
y=(x-1)((x-1);
end
y
A. 3或-3 B. -5 C. -5或5 D. 5或-3
参考答案
一、选择题:BBACB
6.C。7、A。8、A。
9、C,赋值语句要注意变量替换顺序。
10C,当时,,然后循环结束。
11.A,当时要提出循环体,而此时接下来,因此条件为i>10。
12、解析:选A,一个数被2除的余数为1时为奇数。
CDABBC
二、填空题1.下列程序执行后,输出的是= ,=
;;;
2.下面程序是用“等值算法”求最大公约数的程序,由中间有两处错误的算法语句,
请你找出来,并修正.(1) 改为 (2) 改为
3、如图所示的算法程序框图,表示的算法的功能是 ;
4.把下面求1×2×……× (n-1)×n的程序补充完整
5.若输入6时,则下列程序执行后输出的结果是 .
x=input(“x=”)
if x<= 4
y=0.76;
else
y=6+8*(x-3);
end
print(%io(2),y)
参考答案
1.=3,=1 2.(1)a-b=a改为a =a-b;(2)b-a=b改为b =b-a
3、解析:计算并输出使1×3×5×7…× >10 000成立的最小正整数。
4、i<=n ,s=s*i 5、30
三、解答题
1. (I)用辗转相除法求840与1 764的最大公约数.
(II)用更相减损术求440 与556的最大公约数.
解:(I)用辗转相除法求840与1 764 的最大公约数.
1764 = 840×2 + 84 840 = 84×10 +0
所以840与1 764 的最大公约数是84
( II)用更相减损术求440 与556的最大公约数.
556-440 = 116 440-116 = 324 324-116 = 208
208-116 = 92 116-92 = 24 92-24 = 68
68-24 = 44 44-24 = 20 24-20 = 4
20-4 = 16 16-4 = 12 12-4 = 8 8-4 = 4
所以440 与556的最大公约数4.
2.已知二次函数,设计一个算法,判断二次函数的图象与轴交点的个数,并画出程序框图.
解:算法分析:二次函数的图象与轴交点的个数,就是判断一元二次方程有几个实根,要判断与的大小关系,因此这个算法用条件分枝结构.
程序框图如下:
3.设计一个计算1+2+3+…+100的值的算法,并画出程序框图.
解:算法:
S1:设的值为;
S2:设的值为0;
S3:如果执行S4,否则转去执行S7;
S4:计算并将结果代替;
S5:计算并将结果代替;
S6:转去执行S3;
S7:输出的值并结束算法。
程序框图如下:
4. 已知算法:
S1. 输入 x
S2. 若x<-2,则y = x 2+1
S3. 若,则y=x
S4. ,则y = x 2-1
S5. 输出y
将该算法用流程图描述.
解:算法的功能为:
5.已知如下程序,写出该程序所表达的问题,并画出相应的框图.
解:题中所给程序是求的值.
6.用秦九韶算法计算函数时的函数值.
解:
∴
∴
7.用while和for语句写出1~1000内所有能被3整除的自然数之和的算法程序.
解答如下:
8、给出30个数:1,2,4,7,……,其规律是:
第1个数是1,第2个数比第1个数大1, 第3个数
比第2个数大2,第4个数比第3个数大3,依此类推.
要计算这30个数的和,现已给出了该问题算法的程序
框图(如图所示),
(I)请在图中判断框内(1)处和执行框中的(2)处
填上合适的语句,使之能完成该题算法功能;
(II)根据程序框图写出程序.
解:(I)该算法使用了循环结构,因为是求30个数的和,故循环体应执行30次,
其中i是计数变量,因此判断框内的条件就是限制计数变量i的,故应为,算法中的变量p实质是表示参与求和的各个数,由于它也是变化的,且满足第i个数比其前一个数大,第个数比其前一个数大i,故应有.故(1)处应填;(2)处应填
一、选择题
1.下列给出的赋值语句中正确的是( )
A.6=a+5 B.M =-M C.6=a=b D.x-y=10
2.算法S1: m=a
S2: 若b
A.a,b,c,d中最大值 B.a,b,c,d中最小值
C.将a,b,c,d由小到大排序 D.将a,b,c,d由大到小排序
3.已知,,,,根据上述系列等式,可确定和和的最大公约数是( )
A.19 B.3 C.57 D.34
4.求满足的最小正整数,写出它的程序必须用( )
A.输入(出)语句 B.条件语句
C.“while”语句 D.“for”语句
5.以下给出计算的值的四个程序,其中正确的( )
A. B.
C. D.
6、将两个数a=25,b=9交换,使a=9,b=25,下面语句正确一组是 ( )
A B C D
7、条件语句的一般形式是“if A then B else C”,其中B表示的是 ( )
A、满足条件时执行的内容 B、条件语句 C、条件 D、不满足条件时执行的内容
8、for 语句的一般格式为:for i from a to b step c,其中a 的意义是 ( )
A、循环变量初始值 B、循环变量终值
C、循环体 D、循环条件的语句
9、右边程序运行的结果是 ( )
A、1,2,3 B、2,3,1 C、2,3,2 D、3,2,1
10、右边程序运行后的输出结果为 ( )
A、17 B、19 C、21 D、23
11、如图给出的是计算的值的一个程序框图,其中判断框内应填入 ( )A、i>10 B、i<10 C、i>20 D、i<20
12、程序框图,能判断任意输入的数x的奇偶性:其中判断框内的条件是 ( )
A、m=0 B、x=0 C、x=1 D. m=1
13.下面的问题中必须用条件结构才能实现的个数是( )
(1)已知三角形三边长,求三角形的面积;
(2)求方程ax+b=0(a,b为常数)的根;
(3)求三个实数a,b,c中的最大者;
(4)求1+2+3+…+100的值。
A. 4个 B. 3个 C. 2个 D. 1个
14.右边程序执行后输出的结果是( )
A.-1 B.0 C.1 D.2
15.算法:
S1 输入n
S2 判断n是否是2,若n=2,则n满足条件,若n>2,则执行S3
S3 依次从2到n一1检验能不能整除n,若不能整除n,满足上述条件的是 ( )
A.质数 B.奇数 C.偶数 D.约数
16.下图给出的是计算的值的一个程序框图,其中判断框内应填入的条件是( )A.i>100 B.i<=100 C.i>50 D.i<=50
17.给出下面的程序框图,那么其循环体执行的次数是( )
A.500 B.499
C.1000 D.998
18.为了在运行下面的程序之后得到输出y=16,键盘输入x应该是( )
x=input(“x=”)
if x<0
y=(x+1)((x+1);
else
y=(x-1)((x-1);
end
y
A. 3或-3 B. -5 C. -5或5 D. 5或-3
参考答案
一、选择题:BBACB
6.C。7、A。8、A。
9、C,赋值语句要注意变量替换顺序。
10C,当时,,然后循环结束。
11.A,当时要提出循环体,而此时接下来,因此条件为i>10。
12、解析:选A,一个数被2除的余数为1时为奇数。
CDABBC
二、填空题1.下列程序执行后,输出的是= ,=
;;;
2.下面程序是用“等值算法”求最大公约数的程序,由中间有两处错误的算法语句,
请你找出来,并修正.(1) 改为 (2) 改为
3、如图所示的算法程序框图,表示的算法的功能是 ;
4.把下面求1×2×……× (n-1)×n的程序补充完整
5.若输入6时,则下列程序执行后输出的结果是 .
x=input(“x=”)
if x<= 4
y=0.76;
else
y=6+8*(x-3);
end
print(%io(2),y)
参考答案
1.=3,=1 2.(1)a-b=a改为a =a-b;(2)b-a=b改为b =b-a
3、解析:计算并输出使1×3×5×7…× >10 000成立的最小正整数。
4、i<=n ,s=s*i 5、30
三、解答题
1. (I)用辗转相除法求840与1 764的最大公约数.
(II)用更相减损术求440 与556的最大公约数.
解:(I)用辗转相除法求840与1 764 的最大公约数.
1764 = 840×2 + 84 840 = 84×10 +0
所以840与1 764 的最大公约数是84
( II)用更相减损术求440 与556的最大公约数.
556-440 = 116 440-116 = 324 324-116 = 208
208-116 = 92 116-92 = 24 92-24 = 68
68-24 = 44 44-24 = 20 24-20 = 4
20-4 = 16 16-4 = 12 12-4 = 8 8-4 = 4
所以440 与556的最大公约数4.
2.已知二次函数,设计一个算法,判断二次函数的图象与轴交点的个数,并画出程序框图.
解:算法分析:二次函数的图象与轴交点的个数,就是判断一元二次方程有几个实根,要判断与的大小关系,因此这个算法用条件分枝结构.
程序框图如下:
3.设计一个计算1+2+3+…+100的值的算法,并画出程序框图.
解:算法:
S1:设的值为;
S2:设的值为0;
S3:如果执行S4,否则转去执行S7;
S4:计算并将结果代替;
S5:计算并将结果代替;
S6:转去执行S3;
S7:输出的值并结束算法。
程序框图如下:
4. 已知算法:
S1. 输入 x
S2. 若x<-2,则y = x 2+1
S3. 若,则y=x
S4. ,则y = x 2-1
S5. 输出y
将该算法用流程图描述.
解:算法的功能为:
5.已知如下程序,写出该程序所表达的问题,并画出相应的框图.
解:题中所给程序是求的值.
6.用秦九韶算法计算函数时的函数值.
解:
∴
∴
7.用while和for语句写出1~1000内所有能被3整除的自然数之和的算法程序.
解答如下:
8、给出30个数:1,2,4,7,……,其规律是:
第1个数是1,第2个数比第1个数大1, 第3个数
比第2个数大2,第4个数比第3个数大3,依此类推.
要计算这30个数的和,现已给出了该问题算法的程序
框图(如图所示),
(I)请在图中判断框内(1)处和执行框中的(2)处
填上合适的语句,使之能完成该题算法功能;
(II)根据程序框图写出程序.
解:(I)该算法使用了循环结构,因为是求30个数的和,故循环体应执行30次,
其中i是计数变量,因此判断框内的条件就是限制计数变量i的,故应为,算法中的变量p实质是表示参与求和的各个数,由于它也是变化的,且满足第i个数比其前一个数大,第个数比其前一个数大i,故应有.故(1)处应填;(2)处应填
