数学人教A版(2019)选择性必修第三册7.1.1条件概率 课件(共13张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册7.1.1条件概率 课件(共13张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-06 08:04:13 | ||
图片预览



文档简介
(共13张PPT)
数学
选择性必修第三册
第七章 条件概率与全概率公式
7.1.1 条件概率
情景与问题
从生物学中我们知道,生男、生女的概率基本是相等的,这里假定生男、生女的概率相等.如果某个家庭先后生了两个小孩:
(1)当已知较大的女孩是女孩的条件下,较小的女孩是男孩的概率为多少?
(2)当已知两个小孩中有女孩的条件下,两个小孩中有男孩的概率为多少?
尝试与发现
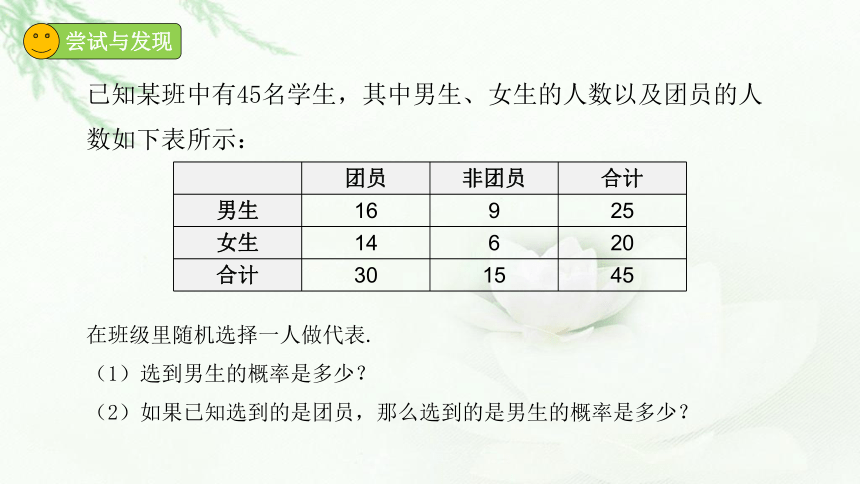
已知某班中有45名学生,其中男生、女生的人数以及团员的人数如下表所示:
在班级里随机选择一人做代表.
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
探究得新知
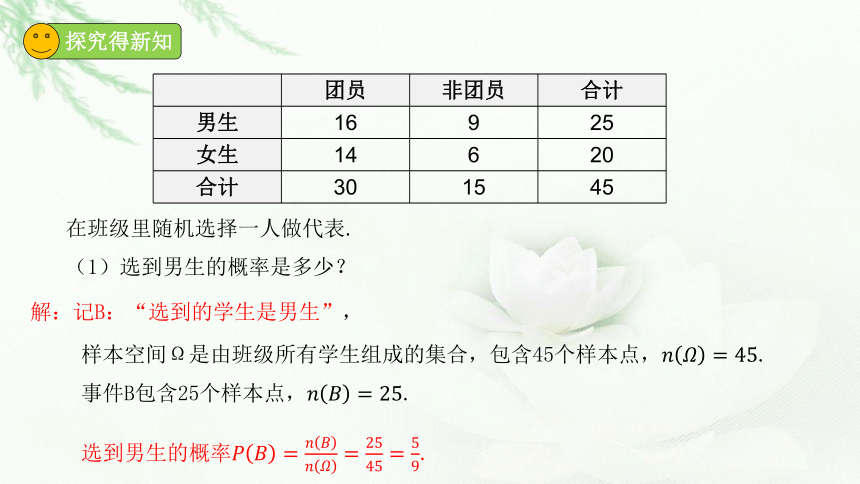
在班级里随机选择一人做代表.
(1)选到男生的概率是多少?
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
解:记B:“选到的学生是男生”,
样本空间Ω是由班级所有学生组成的集合,包含45个样本点,.事件B包含25个样本点,.
选到男生的概率.
探究得新知
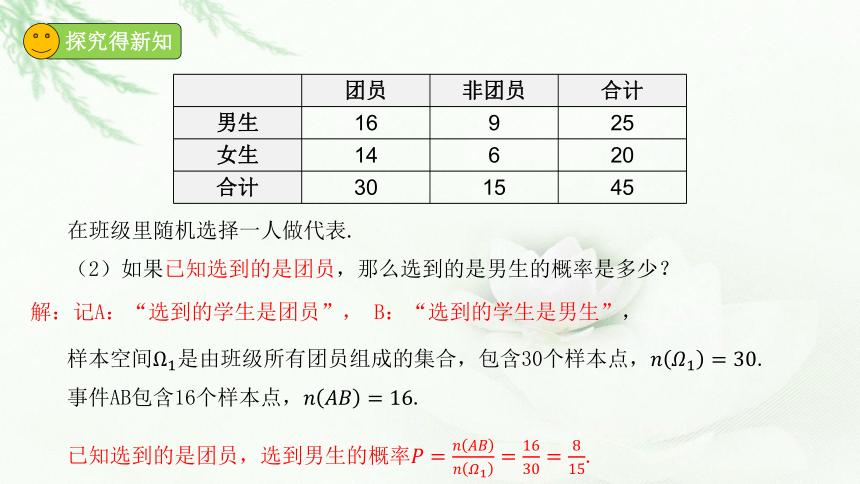
在班级里随机选择一人做代表.
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
解:记A:“选到的学生是团员”, B:“选到的学生是男生”,
样本空间是由班级所有团员组成的集合,包含30个样本点,.事件AB包含16个样本点,.
已知选到的是团员,选到男生的概率.
记A:“选到的学生是团员”, B:“选到的学生是男生”
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
探究得新知
样本空间Ω是由班级所有学生组成的集合
样本空间是由班级所有团员组成的集合
一般地,当事件A发生的概率大于0()时,在事件A发生的条件下事件B发生的概率,称为条件概率,记作.
归纳得定义
例如:已知选到的是团员,选到男生的概率.
记A:“选到的学生是团员”, B:“选到的学生是男生”
样本空间Ω是由班级所有学生组成的集合
.
一般地,当事件A发生的概率大于0()时,已知事件A发生的条件下事件B发生的概率,称为条件概率,记作.
归纳得定义
事件个数法:;
定义法:
比如,若.
一般地,当事件A发生的概率大于0()时,已知事件A发生的条件下事件B发生的概率,称为条件概率,记作.
定义再深化
事件个数法:;
定义法:
当时,当且仅当事件A与B相互独立时,有
乘法公式:
性质
问题再解决
从生物学中我们知道,生男、生女的概率基本是相等的,这里假定生男、生女的概率相等.如果某个家庭先后生了两个小孩:
(1)当已知较大的小孩是女孩的条件下,较小的小孩是男孩的概率为多少?
(2)当已知两个小孩中有女孩的条件下,两个小孩中有男孩的概率为多少?
解:(1)用表示男孩,用表示女孩
样本空间
记A:“较大的小孩是女孩”, B:“较小的小孩是男孩”,
问题再解决
从生物学中我们知道,生男、生女的概率基本是相等的,这里假定生男、生女的概率相等.如果某个家庭先后生了两个小孩:
(1)当已知较大的小孩是女孩的条件下,较小的小孩是男孩的概率为多少?
(2)当已知两个小孩中有女孩的条件下,两个小孩中有男孩的概率为多少?
解:(2)用表示男孩,用表示女孩
样本空间
记C:“两个小孩中有女孩”, D:“两个小孩中有男孩”,
新知应用
抛掷红、蓝两颗质地均匀的骰子,记A:蓝色骰子的点数为5或6;B:两颗骰子的点数之和大于7,求在事件A发生的条件下事件B发生的概率.
解:用表示抛掷结果,表示红色骰子的点数,表示蓝色骰子的点数.
样本空间可记为
一般地,当事件A发生的概率大于0()时,已知事件A发生的条件下事件B发生的概率,称为条件概率,记作.
课堂总结
事件个数法:;
定义法:
当时,当且仅当事件A与B相互独立时,有
乘法公式:
性质
数学
选择性必修第三册
第七章 条件概率与全概率公式
7.1.1 条件概率
情景与问题
从生物学中我们知道,生男、生女的概率基本是相等的,这里假定生男、生女的概率相等.如果某个家庭先后生了两个小孩:
(1)当已知较大的女孩是女孩的条件下,较小的女孩是男孩的概率为多少?
(2)当已知两个小孩中有女孩的条件下,两个小孩中有男孩的概率为多少?
尝试与发现
已知某班中有45名学生,其中男生、女生的人数以及团员的人数如下表所示:
在班级里随机选择一人做代表.
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
探究得新知
在班级里随机选择一人做代表.
(1)选到男生的概率是多少?
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
解:记B:“选到的学生是男生”,
样本空间Ω是由班级所有学生组成的集合,包含45个样本点,.事件B包含25个样本点,.
选到男生的概率.
探究得新知
在班级里随机选择一人做代表.
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
解:记A:“选到的学生是团员”, B:“选到的学生是男生”,
样本空间是由班级所有团员组成的集合,包含30个样本点,.事件AB包含16个样本点,.
已知选到的是团员,选到男生的概率.
记A:“选到的学生是团员”, B:“选到的学生是男生”
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少?
探究得新知
样本空间Ω是由班级所有学生组成的集合
样本空间是由班级所有团员组成的集合
一般地,当事件A发生的概率大于0()时,在事件A发生的条件下事件B发生的概率,称为条件概率,记作.
归纳得定义
例如:已知选到的是团员,选到男生的概率.
记A:“选到的学生是团员”, B:“选到的学生是男生”
样本空间Ω是由班级所有学生组成的集合
.
一般地,当事件A发生的概率大于0()时,已知事件A发生的条件下事件B发生的概率,称为条件概率,记作.
归纳得定义
事件个数法:;
定义法:
比如,若.
一般地,当事件A发生的概率大于0()时,已知事件A发生的条件下事件B发生的概率,称为条件概率,记作.
定义再深化
事件个数法:;
定义法:
当时,当且仅当事件A与B相互独立时,有
乘法公式:
性质
问题再解决
从生物学中我们知道,生男、生女的概率基本是相等的,这里假定生男、生女的概率相等.如果某个家庭先后生了两个小孩:
(1)当已知较大的小孩是女孩的条件下,较小的小孩是男孩的概率为多少?
(2)当已知两个小孩中有女孩的条件下,两个小孩中有男孩的概率为多少?
解:(1)用表示男孩,用表示女孩
样本空间
记A:“较大的小孩是女孩”, B:“较小的小孩是男孩”,
问题再解决
从生物学中我们知道,生男、生女的概率基本是相等的,这里假定生男、生女的概率相等.如果某个家庭先后生了两个小孩:
(1)当已知较大的小孩是女孩的条件下,较小的小孩是男孩的概率为多少?
(2)当已知两个小孩中有女孩的条件下,两个小孩中有男孩的概率为多少?
解:(2)用表示男孩,用表示女孩
样本空间
记C:“两个小孩中有女孩”, D:“两个小孩中有男孩”,
新知应用
抛掷红、蓝两颗质地均匀的骰子,记A:蓝色骰子的点数为5或6;B:两颗骰子的点数之和大于7,求在事件A发生的条件下事件B发生的概率.
解:用表示抛掷结果,表示红色骰子的点数,表示蓝色骰子的点数.
样本空间可记为
一般地,当事件A发生的概率大于0()时,已知事件A发生的条件下事件B发生的概率,称为条件概率,记作.
课堂总结
事件个数法:;
定义法:
当时,当且仅当事件A与B相互独立时,有
乘法公式:
性质
