人教版七年级数学下册 5.1.3同位角、内错角、同旁内角 一课一练(word版含答案)
文档属性
| 名称 | 人教版七年级数学下册 5.1.3同位角、内错角、同旁内角 一课一练(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 143.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-06 00:00:00 | ||
图片预览




文档简介
5.1.3同位角、内错角、同旁内角
一、选择题
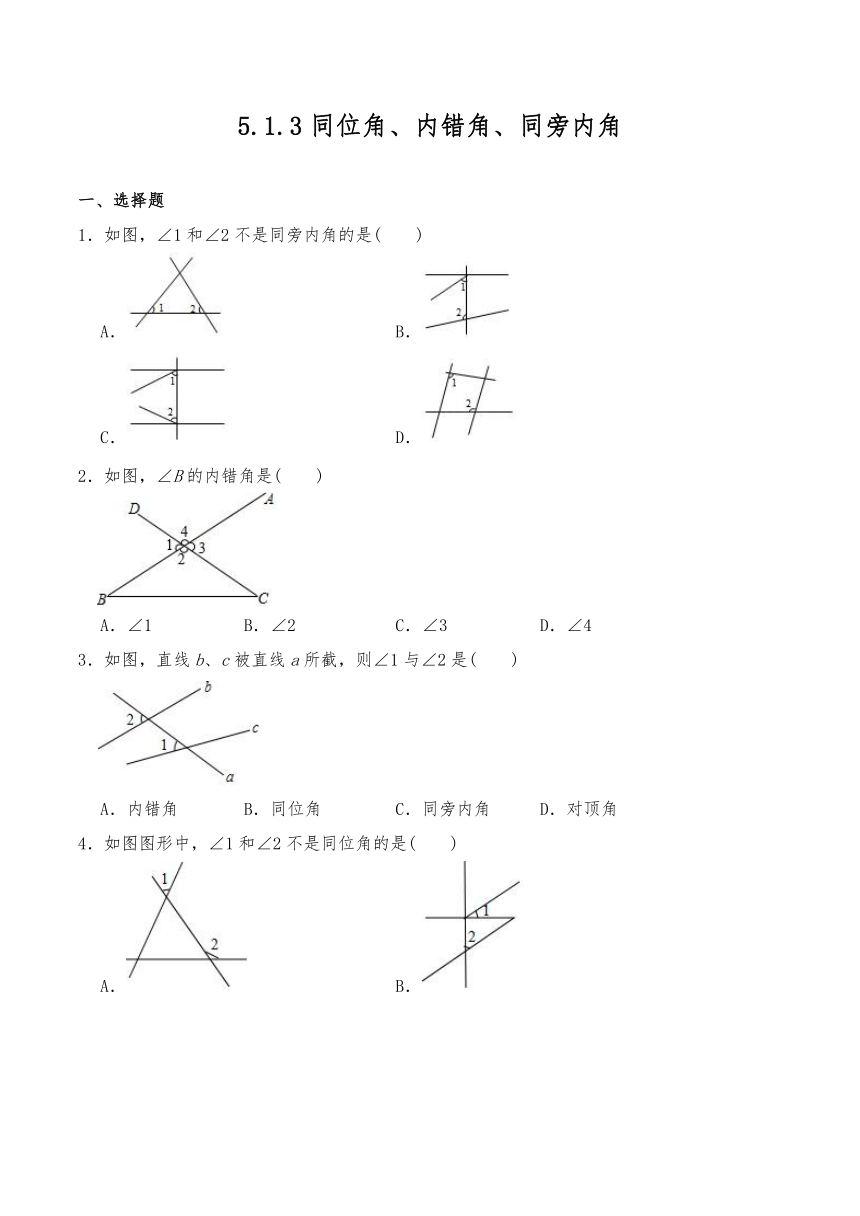
1.如图,∠1和∠2不是同旁内角的是( )
A. B.
C. D.
2.如图,∠B的内错角是( )
A.∠1 B.∠2 C.∠3 D.∠4
3.如图,直线b、c被直线a所截,则∠1与∠2是( )
A.内错角 B.同位角 C.同旁内角 D.对顶角
4.如图图形中,∠1和∠2不是同位角的是( )
A. B.
C. D.
5.下列所示的四个图形中,∠1和∠2是同位角的是( )
A.②③ B.①②③ C.③④ D.①②④
6.下列图中,∠1与∠2是同位角的是( )
A. B.
C. D.
7.下列所示的四个图形中,∠1和∠2是同位角的是( )
A.②③ B.①②③ C.①②④ D.①④
8.如图,给出以下说法:①∠B和∠1是同旁内角;②∠3和∠4是内错角;③∠B和∠AEC是同位角;④∠A和∠3是内错角;⑤∠2和∠3是对顶角,其中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
9.如图所示,下列选项中是一组同位角的是( )
A.∠1和∠3 B.∠2和∠5 C.∠3和∠4 D.∠3和∠5
10.如图所示,下列说法:
①∠1与∠C是同位角;
②∠2与∠C是内错角;
③∠3与∠B是同旁内角;
④∠3与∠C是同旁内角.
其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
二、填空题
11.如图,∠B的内错角是 .
12.如图所示的图形中,同位角有 对.
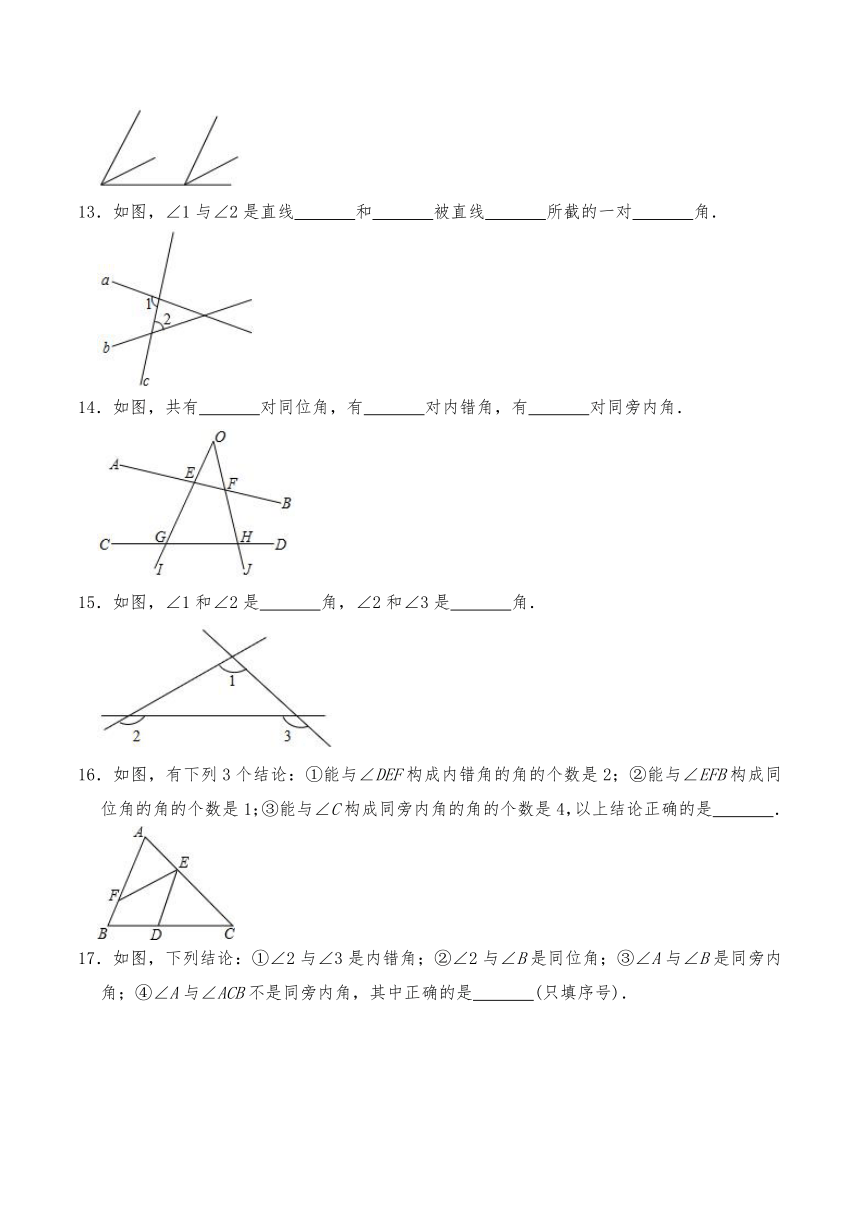
13.如图,∠1与∠2是直线 和 被直线 所截的一对 角.
14.如图,共有 对同位角,有 对内错角,有 对同旁内角.
15.如图,∠1和∠2是 角,∠2和∠3是 角.
16.如图,有下列3个结论:①能与∠DEF构成内错角的角的个数是2;②能与∠EFB构成同位角的角的个数是1;③能与∠C构成同旁内角的角的个数是4,以上结论正确的是 .
17.如图,下列结论:①∠2与∠3是内错角;②∠2与∠B是同位角;③∠A与∠B是同旁内角;④∠A与∠ACB不是同旁内角,其中正确的是 (只填序号).
18.如图,有下列判断:
①∠A与∠1是同位角;
②∠A与∠B是同旁内角;
③∠4与∠C是内错角;
④∠2与∠3是对顶角.其中正确的是 (填序号).
三、解答题
19.分别指出下列图中的同位角、内错角、同旁内角.
20.根据图形填空:
(1)若直线ED、BC被直线AB所截,则∠1和 是同位角;
(2)若直线ED、BC被直线AF所截,则∠3和 是内错角;
(3)∠1和∠3是直线AB、AF被直线 所截构成的内错角.
(4)∠2和∠4是直线AB、 被直线BC所截构成的 角.
21.如图所示,找出图中的同位角、内错角、同旁内角(仅限于用数字表示).
22.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3;
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2,∠3的度数.
23.如图,已知∠DAB=65°,∠1=∠C.
(1)在图中画出∠DAB的对顶角;
(2)写出∠1的同位角;
(3)写出∠C的同旁内角;
(4)求∠B的度数.
24.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线l1,l2被直线l3所截,在这个基本图形中,形成了 对同旁内角.
(2)如图2,平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有 对同旁内角.
(3)平面内四条直线两两相交,最多可以形成 对同旁内角.
(4)平面内n条直线两两相交,最多可以形成 对同旁内角.
答案
一、选择题
1.D.2.A.3.B.4.B.5.D.6.B.7.C.8.B.9.B.10.C.
二、填空题
11.∠BAD.
12.2.
13.a;b;c;内错.
14.20;12;12.
15.同位,同旁内.
16.①②.
17.①②③.18.①②④.
三、解答题
19.如图1,
同位角有:∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8;
内错角有:∠3与∠6,∠4与∠5;
同旁内角有:∠3与∠5,∠4与∠6.
如图2,
同位角有:∠1与∠3,∠2与∠4;
同旁内角有:∠3与∠2.
20.(1)如图:若ED,BC被AB所截,则∠1与∠2是同位角,
(2)若ED,BC被AF所截,则∠3与∠4是内错角,
(3)∠1 与∠3是AB和AF被ED所截构成的内错角,
(4)∠2与∠4是AB和AF被BC所截构成的同位角.
21.由图可得:
同位角:∠1与∠3,∠3与∠5;
内错角:∠1与∠4,∠4与∠5;
同旁内角:∠1与∠2,∠6与∠5.
22.(1)如图所示:
(2)∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
∵∠1+∠3=180°,
∴x+4x=180°,
解得:x=36°,
故∠3=36°,∠2=72°,∠1=144°.
23.(1)如图,∠GAH即为所求;
(2)∠1的同位角是∠DAB;
(3)∠C的同旁内角是∠B和∠ADC;
(4)因为∠1=∠C,
所以AE∥BC.
所以∠DAB+∠B=180°,
又因为∠DAB=65°,
所以∠B=115°.
24.(1)直线l1,l2被直线l3所截,在这个基本图形中,形成了2对同旁内角.
(2)平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有6对同旁内角.
(3)平面内四条直线两两相交,最多可以形成24对同旁内角.
(4)平面内n条直线两两相交,最多可以形成n(n﹣1)(n﹣2)对同旁内角
故答案为:(1)2;(2)6;(3)24;(4)n(n﹣1)(n﹣2)
一、选择题
1.如图,∠1和∠2不是同旁内角的是( )
A. B.
C. D.
2.如图,∠B的内错角是( )
A.∠1 B.∠2 C.∠3 D.∠4
3.如图,直线b、c被直线a所截,则∠1与∠2是( )
A.内错角 B.同位角 C.同旁内角 D.对顶角
4.如图图形中,∠1和∠2不是同位角的是( )
A. B.
C. D.
5.下列所示的四个图形中,∠1和∠2是同位角的是( )
A.②③ B.①②③ C.③④ D.①②④
6.下列图中,∠1与∠2是同位角的是( )
A. B.
C. D.
7.下列所示的四个图形中,∠1和∠2是同位角的是( )
A.②③ B.①②③ C.①②④ D.①④
8.如图,给出以下说法:①∠B和∠1是同旁内角;②∠3和∠4是内错角;③∠B和∠AEC是同位角;④∠A和∠3是内错角;⑤∠2和∠3是对顶角,其中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
9.如图所示,下列选项中是一组同位角的是( )
A.∠1和∠3 B.∠2和∠5 C.∠3和∠4 D.∠3和∠5
10.如图所示,下列说法:
①∠1与∠C是同位角;
②∠2与∠C是内错角;
③∠3与∠B是同旁内角;
④∠3与∠C是同旁内角.
其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
二、填空题
11.如图,∠B的内错角是 .
12.如图所示的图形中,同位角有 对.
13.如图,∠1与∠2是直线 和 被直线 所截的一对 角.
14.如图,共有 对同位角,有 对内错角,有 对同旁内角.
15.如图,∠1和∠2是 角,∠2和∠3是 角.
16.如图,有下列3个结论:①能与∠DEF构成内错角的角的个数是2;②能与∠EFB构成同位角的角的个数是1;③能与∠C构成同旁内角的角的个数是4,以上结论正确的是 .
17.如图,下列结论:①∠2与∠3是内错角;②∠2与∠B是同位角;③∠A与∠B是同旁内角;④∠A与∠ACB不是同旁内角,其中正确的是 (只填序号).
18.如图,有下列判断:
①∠A与∠1是同位角;
②∠A与∠B是同旁内角;
③∠4与∠C是内错角;
④∠2与∠3是对顶角.其中正确的是 (填序号).
三、解答题
19.分别指出下列图中的同位角、内错角、同旁内角.
20.根据图形填空:
(1)若直线ED、BC被直线AB所截,则∠1和 是同位角;
(2)若直线ED、BC被直线AF所截,则∠3和 是内错角;
(3)∠1和∠3是直线AB、AF被直线 所截构成的内错角.
(4)∠2和∠4是直线AB、 被直线BC所截构成的 角.
21.如图所示,找出图中的同位角、内错角、同旁内角(仅限于用数字表示).
22.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图,标出∠1,∠2,∠3;
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2,∠3的度数.
23.如图,已知∠DAB=65°,∠1=∠C.
(1)在图中画出∠DAB的对顶角;
(2)写出∠1的同位角;
(3)写出∠C的同旁内角;
(4)求∠B的度数.
24.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线l1,l2被直线l3所截,在这个基本图形中,形成了 对同旁内角.
(2)如图2,平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有 对同旁内角.
(3)平面内四条直线两两相交,最多可以形成 对同旁内角.
(4)平面内n条直线两两相交,最多可以形成 对同旁内角.
答案
一、选择题
1.D.2.A.3.B.4.B.5.D.6.B.7.C.8.B.9.B.10.C.
二、填空题
11.∠BAD.
12.2.
13.a;b;c;内错.
14.20;12;12.
15.同位,同旁内.
16.①②.
17.①②③.18.①②④.
三、解答题
19.如图1,
同位角有:∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8;
内错角有:∠3与∠6,∠4与∠5;
同旁内角有:∠3与∠5,∠4与∠6.
如图2,
同位角有:∠1与∠3,∠2与∠4;
同旁内角有:∠3与∠2.
20.(1)如图:若ED,BC被AB所截,则∠1与∠2是同位角,
(2)若ED,BC被AF所截,则∠3与∠4是内错角,
(3)∠1 与∠3是AB和AF被ED所截构成的内错角,
(4)∠2与∠4是AB和AF被BC所截构成的同位角.
21.由图可得:
同位角:∠1与∠3,∠3与∠5;
内错角:∠1与∠4,∠4与∠5;
同旁内角:∠1与∠2,∠6与∠5.
22.(1)如图所示:
(2)∵∠1=2∠2,∠2=2∠3,
∴设∠3=x,则∠2=2x,∠1=4x,
∵∠1+∠3=180°,
∴x+4x=180°,
解得:x=36°,
故∠3=36°,∠2=72°,∠1=144°.
23.(1)如图,∠GAH即为所求;
(2)∠1的同位角是∠DAB;
(3)∠C的同旁内角是∠B和∠ADC;
(4)因为∠1=∠C,
所以AE∥BC.
所以∠DAB+∠B=180°,
又因为∠DAB=65°,
所以∠B=115°.
24.(1)直线l1,l2被直线l3所截,在这个基本图形中,形成了2对同旁内角.
(2)平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有6对同旁内角.
(3)平面内四条直线两两相交,最多可以形成24对同旁内角.
(4)平面内n条直线两两相交,最多可以形成n(n﹣1)(n﹣2)对同旁内角
故答案为:(1)2;(2)6;(3)24;(4)n(n﹣1)(n﹣2)
