选择性必修三2.1气体实验定律 练习(word版含答案)
文档属性
| 名称 | 选择性必修三2.1气体实验定律 练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-05 23:39:10 | ||
图片预览



文档简介
粤教版(2019)选择性必修三 2.1 气体实验定律(Ⅰ)
一、单选题
1.如图所示,一端封闭的玻璃管,开口向下竖直插在水银槽里,管内封有长度分别为l1和l2的两段理想气体。外界温度和大气压均不变,当将管慢慢地向上提起时,管内气柱的长度( )
A.l1变小,l2变大 B.l1变大,l2变小
C.l1、l2都变小 D.l1、l2都变大
2.下列不是描述气体状态参量的物理量是( )
A.压强 B.体积
C.质量 D.温度
3.如图所示为某同学设计的喷药装置,内部装有8L药液,上部密封1atm的空气1L,保持阀门关闭,再充入1atm的空气0.2L,设在所有过程中空气可看成理想气体,且温度不变,下列说法错误的是( )
A.充气后,密封气体的压强增大为1.2atm
B.充气后,密封气体的分子平均动能不变
C.打开阀门后,密封气体对外界做正功
D.打开阀门后,不再充气也能把药液喷光
4.如图是一竖直放置开口向上的均匀玻璃管,内用水银柱封有一定质量的理想气体,水银与玻璃管间摩擦力不计,开始时手拿玻璃管处于平衡状态,后松开手,玻璃管沿竖直方向运动,最后达到稳定状态的过程中,下列说法中正确的是 ( )
A.刚开始瞬间,玻璃管的加速度一定大于重力加速度g
B.刚开始短时间内,试管内的气体压强一定在逐渐变小
C.刚开始短时间内,玻璃管的加速度在逐渐变小
D.以上情况一定均会发生
5.一个气泡从水面下深处缓缓上升到水面,假定水的温度均匀,水面上方的压强为,则气泡到达水面时的体积为原来的( )
A.3倍 B.4倍 C.5倍 D.6倍
6.现有一个容积为400L的医用氧气罐,内部气体可视为理想气体,压强为15MPa,为了使用方便,用一批相同规格的小型氧气瓶(瓶内视为真空)进行分装,发现恰好能装满40个小氧气瓶,分装完成后原医用氧气罐及每个小氧气瓶内气体的压强均为3MPa,不考虑分装过程中温度的变化,则每个小氧气瓶的容积为( )
A.20L B.40L C.50L D.60L
7.医用氧气钢瓶的容积,室内常温下充装氧气后,氧气钢瓶内部压强,释放氧气时瓶内压强不能低于。病人一般在室内常温下吸氧时,每分钟需要消耗下氧气,室内常温下,一瓶氧气能供一个病人吸氧的最长时间为( )
A.23小时 B.33.5小时 C.46小时 D.80小时
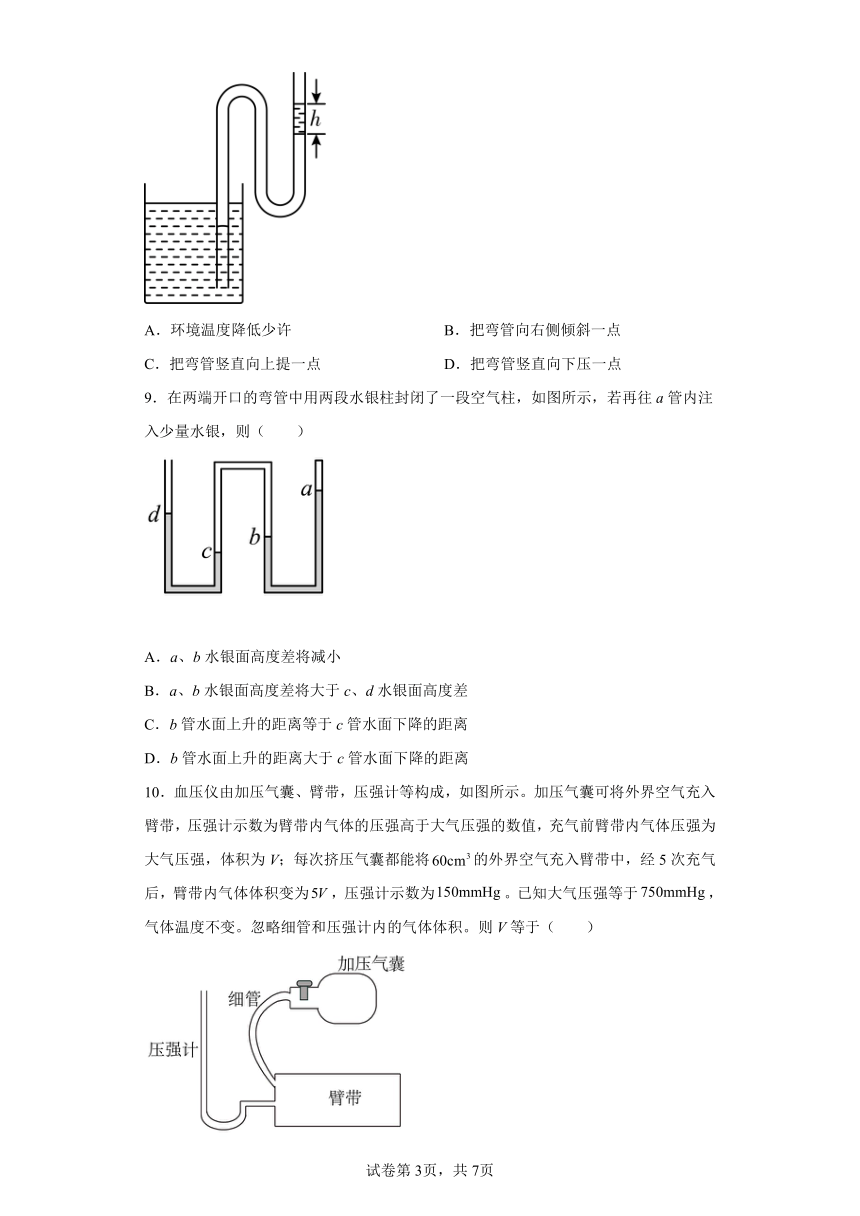
8.如图,两端开口的弯管,左管插入水银槽中,右管有一小段水银柱,中间封有一段空气。能使得左管内部水银面相对水银槽上升的操作是( )
A.环境温度降低少许 B.把弯管向右侧倾斜一点
C.把弯管竖直向上提一点 D.把弯管竖直向下压一点
9.在两端开口的弯管中用两段水银柱封闭了一段空气柱,如图所示,若再往a管内注入少量水银,则( )
A.a、b水银面高度差将减小
B.a、b水银面高度差将大于c、d水银面高度差
C.b管水面上升的距离等于c管水面下降的距离
D.b管水面上升的距离大于c管水面下降的距离
10.血压仪由加压气囊、臂带,压强计等构成,如图所示。加压气囊可将外界空气充入臂带,压强计示数为臂带内气体的压强高于大气压强的数值,充气前臂带内气体压强为大气压强,体积为V;每次挤压气囊都能将的外界空气充入臂带中,经5次充气后,臂带内气体体积变为,压强计示数为。已知大气压强等于,气体温度不变。忽略细管和压强计内的气体体积。则V等于( )
A. B. C. D.
11.如图所示,粗细均匀竖直放置的玻璃管中,P为一小活塞,有一段水银柱将封闭在玻璃管中的空气分成上、下两部分,活塞和水银柱都静止不动。现在用力向下压活塞,使得活塞向下移动一段距离L,同时水银柱将向下缓慢移动一段距离H,在此过程中温度不变,则有( )
A.L>H B.L12.在“探究等温情况下一定质量气体压强与体积的关系”的实验中,下列操作正确的是( )
A.调节空气柱长度后立刻读数
B.拉上窗帘防止阳光直射玻璃管
C.推拉活塞时,为了防止手滑应该用手紧握玻璃管
D.实验中若密封橡胶帽脱落,应立刻堵住后继续实验
13.活塞式真空泵的工作原理如图,抽气筒与被抽密闭容器通过自动阀门相连,当活塞从抽气筒的左端向右移动到右端过程中,阀门自动开启,密闭容器内的气体流入抽气筒,活塞从右端向左移动到左端过程中,阀门自动关闭,抽气筒内活塞左侧的气体被排出,即完成一次抽气过程,如此往复,密闭容器内的气体压强越来越小。若密闭容器的容积为V,抽气筒的容积为0.1V,抽气前密闭容器内气体的压强为p0。抽气过程中气体的温度不变,若第1次抽气过程中被抽出的气体质量为m1,第2次抽气过程中被抽出的气体质量为m2,则m2∶m1为( )
A.1 B.0.9∶1.1 C.1∶1.1 D.1∶1.12
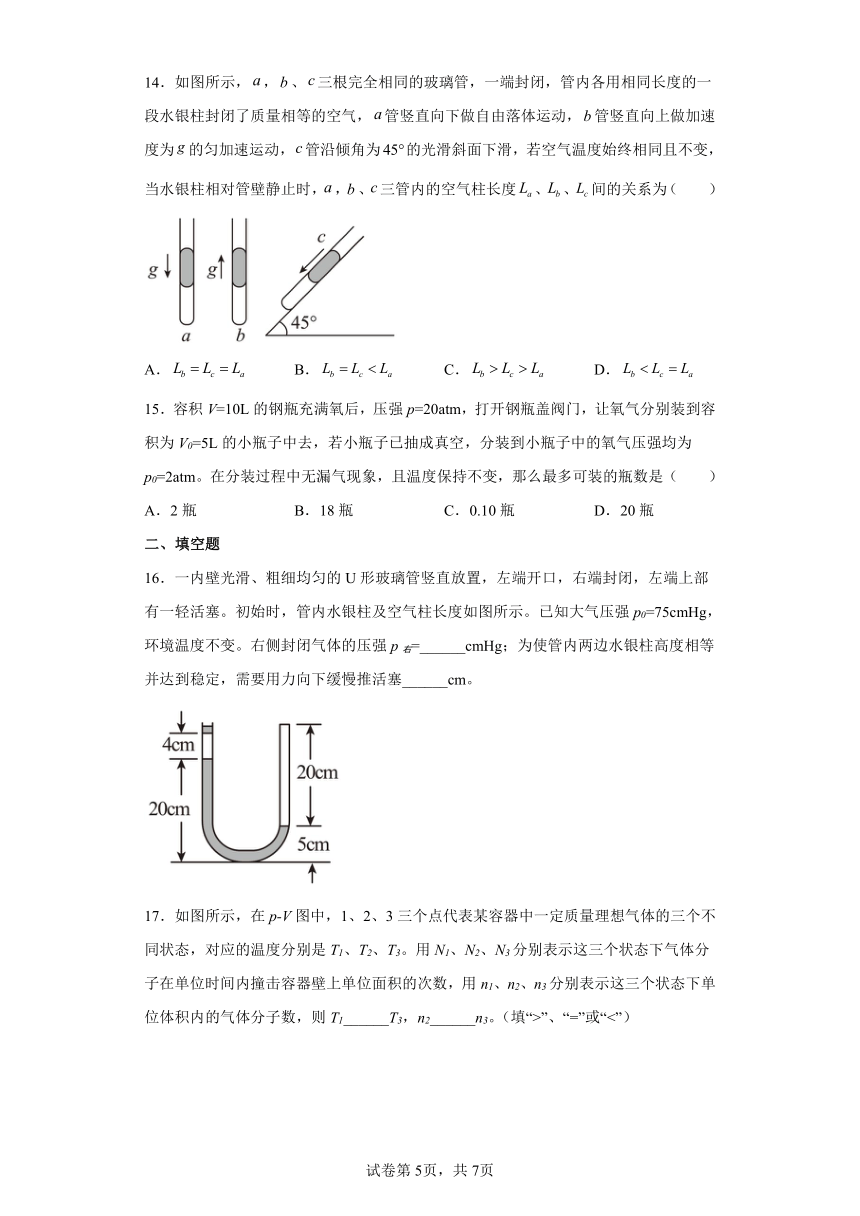
14.如图所示,,、三根完全相同的玻璃管,一端封闭,管内各用相同长度的一段水银柱封闭了质量相等的空气,管竖直向下做自由落体运动,管竖直向上做加速度为的匀加速运动,管沿倾角为的光滑斜面下滑,若空气温度始终相同且不变,当水银柱相对管壁静止时,,、三管内的空气柱长度、、间的关系为( )
A. B. C. D.
15.容积V=10L的钢瓶充满氧后,压强p=20atm,打开钢瓶盖阀门,让氧气分别装到容积为V0=5L的小瓶子中去,若小瓶子已抽成真空,分装到小瓶子中的氧气压强均为p0=2atm。在分装过程中无漏气现象,且温度保持不变,那么最多可装的瓶数是( )
A.2瓶 B.18瓶 C.0.10瓶 D.20瓶
二、填空题
16.一内壁光滑、粗细均匀的U形玻璃管竖直放置,左端开口,右端封闭,左端上部有一轻活塞。初始时,管内水银柱及空气柱长度如图所示。已知大气压强p0=75cmHg,环境温度不变。右侧封闭气体的压强p右=______cmHg;为使管内两边水银柱高度相等并达到稳定,需要用力向下缓慢推活塞______cm。
17.如图所示,在p-V图中,1、2、3三个点代表某容器中一定质量理想气体的三个不同状态,对应的温度分别是T1、T2、T3。用N1、N2、N3分别表示这三个状态下气体分子在单位时间内撞击容器壁上单位面积的次数,用n1、n2、n3分别表示这三个状态下单位体积内的气体分子数,则T1______T3,n2______n3。(填“>”、“=”或“<”)
18.已知地球大气层的厚度h远小于地球半径R,空气平均摩尔质量为M,阿伏加德罗常数为NA,大气层中空气的总质量为m,重力加速度为g.可以估算出地球大气层空气分子总数为_____________,地面大气压强为______________.
19.如图所示,粗细均匀的竖直倒置的U形管右端封闭,左端开口插入水银槽中,封闭着两段空气柱1和2,已知,,外界大气压强为75cmHg,则空气柱1的压强为___________空气柱2的压强为___________。
三、解答题
20.若已知大气压强为p0,图中各装置均处于静止状态,液体密度均为ρ,重力加速度为g,求各被封闭气体的压强。
21.随着社会工业化的发展,对环境的污染越来越严重,尤其是对居民日常饮用水的污染也不可小觑,因此经过特殊工艺处理的桶装水也就走进了千家万户。如图甲是一种桶装水手压式压水器,按压手压头,能够把一定量的外界空气压入密闭水桶内,水从出水管流出,如图乙是简化的原理图,初始时桶内的空气体积为,出水管竖直部分内外液面相平,出水口与桶内水面的高度差为,压水器气囊的容积,水桶的横截面积为。空气可视为理想气体,出水管内水的体积可忽略不计,水的密度,外界大气压强,取。
(ⅰ)若环境温度不变,假若第一次按压后,水没有流出,求此时桶内空气的压强;
(ⅱ)若环境温度不变,按压出了1.0L水,求压入的外界空气的体积。
22.如图,两个相同的内壁光滑的薄壁汽缸和,质量均为,用质量均为的活塞封闭同种气体,体积都为,汽缸的开口处有卡环可以防止活塞离开汽缸。活塞跟汽缸的缸底用细线相连后跨过滑轮,斜面光滑,倾角为。已知大气对活塞的压力等于活塞重力的2.25倍,且,重力加速度为。在外力的作用下,系统一开始处于静止状态,细线绷紧。现撤去外力,让和一起运动,待系统稳定后,求
(1)和运动的加速度大小;
(2)若汽缸中温度不变,汽缸中气体体积变为多少?
23.某个容器的容积是10 L,所装气体的压强是2.0×106 Pa、如果温度保持不变,把容器的开关打开以后,容器里剩下的气体是原来的百分之几?(设大气压是1.0×105 Pa)
24.如图所示,在长为l=57 cm、一端封闭且另一端开口向上的竖直玻璃管内,用4 cm高的水银柱封闭着51 cm长的理想气体,管内外气体的温度均为33 ℃.现将水银缓慢注入管中,直到水银面与管口相平.此时管中气体的压强为多少?新注入水银柱的高度为多少?(大气压强为p0=76 cmHg)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【详解】
当将管慢慢地向上提起时,假设上段空气柱长度不变,则下段空气柱体积增大,由玻意耳定律可知压强减小,从而导致上段气体压强减小,因此上段气体体积增大,故l1、l2都变大,故ABC错误,D正确。
故选D。
2.C
【详解】
描述气体的状态参量,有压强、体积、温度。
故选C。
3.D
【详解】
A.把充入的气体和原气体作为整体:气体做等温变化,根据玻意耳定律可得
解得
故A正确,不符合题意;
B.温度是平均动能的标志,温度不变,所以分子的平均动能不变,故B正确,不符合题意;
C.充气后封闭气体压强变为1.2atm,大于大气压强,所以打开阀门后,气体膨胀,对外界做功,故C正确,不符合题意;
D.膨胀过程温度不变属于等温变化,若都喷完容器中的水,由
得喷完容器中的水后,容器的气体压强小于外界气体压强,所以水不能喷完,故D错误,符合题意。
故选D。
4.D
【详解】
一开始玻璃管处于平衡状态,放手后,玻璃管可能速度向上,或者向下,或者为零。刚开始运动时,玻璃管的内部气体的压强大于外部,所以玻璃管的加速度大于重力加速度g;最初水银所受合力为零,当玻璃管向下或向下运动后,内部气体压强减小,内外气体压强差减少,所以最初的短时间内,水银的加速度在逐渐变大,玻璃管的加速度逐渐变逐渐变小。
故选D。
5.C
【详解】
气泡在水面下40m深处的压强为
根据玻意耳定律,可得
解得
故选C。
6.B
【详解】
设每个小氧气瓶的容积为V0,以医用氧气罐中所有氧气为研究对象,初态:p1=15MPa,V1=400L;末态:p2=3MPa,V2=40V0+400L;因为不考虑温度变化,由玻意耳定律有
代入数据得V0=40L,B正确。
故选B。
7.C
【详解】
由题意可知,气体的温度不变,由玻意耳定律可得
解得
一瓶氧气能供一个病人吸氧的最长时间为
故C正确,ABD错误。
故选C。
8.B
【详解】
左管内水银面相对水银槽内的水银的高度差等于右管中水银柱的高度h,则要使得左管内部水银面相对水银槽上升,则必须要减小h,可把弯管向右侧倾斜一点,将水银柱的竖直高度减小。另外三个方法均不能使左管内部水银面相对水银槽上升。
故选B。
9.D
【详解】
AB.向a管注入水后,封闭气体压强变大,气体体积减小,a、b两液面高度差以及c、d液面高度差都变大;由p=p0+h可知ab水银面高度差等于cd水银面高度差,故AB错误;
CD.向a管注入水后,b管水银面上升,c管水银面下降,因封闭气体压强变大,气体体积减小,所以b管水面上升的距离大于c管水面下降的距离,故C错误,D正确。
故选D。
10.D
【详解】
根据玻意耳定律可知
已知
,,
代入数据整理得
故选D。
11.A
【详解】
题目没说压力多大,可以采用极限法分析,不妨设其为无穷大,这时空气柱的体积几乎都被压缩为零。显然,活塞移动的距离要比水银柱移动的距离多A部分空气柱的长度,即L比H大。
故选A。
【点睛】
在单调函数的变化过程中,可以应用极限法定性分析物理量之间的变化关系。例如,本题中,压强与体积之间的变化关系是减函数,可以采用极限法分析当压强为无穷大时对应的体积情况;活塞移动距离与气体体积减小量之间的变化关系是增函数,可以采用极限法分析当体积为零时对应的活塞移动的距离。
12.B
【详解】
A.调节空气柱长度的过程中,外界对气体做功,气体温度发生变化,为保持气体温度不变,调节空气柱长度后不要立即读数,要等气体状态稳定后再读数,故A错误;
B.实验过程要保持气体温度不变,拉上窗帘防止阳光直射玻璃管,所以B正确;
C.当用手直接握在注射器上时,手的温度可能改变气体的温度,所以不要用手直接握在注射器上,则C错误;
D.实验时要保持气体的质量不变,实验中若密封橡胶帽脱落,注射器内气体的质量发生变化,则不能继续实验,所以D错误;
故选B。
13.C
【详解】
根据玻意耳定律,第1次抽气过程
第2次抽气过程
而正比于,正比于,所以
故选C。
14.D
【详解】
设大气压为。对管,管竖直向下做自由落体运动,处于完全失重状态,封闭气体的压强等于大气压,即。
对管,以水银为研究对象,根据牛顿第二定律得
得
对管,以水银为研究对象,根据牛顿第二定律得
对管和水银整体,有
得
解得
可得
根据玻意耳定律有,可得,ABC错误,D正确。
故选D。
15.B
【详解】
由玻意耳定律得
pV=p1V1
即
20atm×10L=2atm×V1
解得
V1=100L
最多可装的瓶数是
瓶
故选B。
16. 90 9.417
【详解】
[1]
[2]两边水银柱一样高,则左边下降右边上升各7.5cm。所以右边被封气体高度变为12.5cm,对右边气体,由玻意耳定律:
此时左侧气体压强也为p2。
对于左侧气体,由玻意耳定律:
所以活塞下降距离为:
17. = >
【详解】
[1]由于在1、3两状态下,有
则T1= T3。
[2]根据题图可知,2状态的体积小于3状态的体积,又气体分子总数不变,有n2>n3。
18.
【详解】
[1]地球大气层空气分子总数为,
[2]大气压强由于重力作用产生,即有 ;
19. 60cmHg 72cmHg
【详解】
[1]以气柱1作为研究对象有
p1=p0-ph1=60cmHg
[2]以气柱2作为研究对象有
pB=p1+ph2=72cmHg
20.甲:;乙:;丙:;丁:;戊:,
【详解】
题图甲中,以高为h的液柱为研究对象,由平衡条件知
解得
题图乙中,以B液面为研究对象,由平衡条件知
解得
题图丙中,以B液面为研究对象,由平衡条件有
解得
题图丁中,以A液面为研究对象,由平衡条件得
所以
题图戊中,从开口端开始计算,右端大气压强为p0,同种液体同一水平面上的压强相同,
所以b气柱的压强为
故a气柱的压强为
21.(ⅰ);(ⅱ)
【详解】
(ⅰ)设此时桶内空气的压强为p,由理想气体状态方程得
解得
(ⅱ)设流出水后,液面下降的高度为,则
此时桶中空气的压强
体积
设桶中空气在压强时的体积为,由玻意耳定律得
压入的外界空气的体积
解得
22.(1);(2)
【详解】
(1)当系统处于光滑斜面时,对系统分析,则有
解得
(2)系统均静止时,对中活塞分析,则有
解得
加速运动时对中活塞,则有
解得
由玻意耳定律,则有
解得
23.5%
【详解】
以原来气体为研究对象,设原来的气体体积为V1,膨胀后气体的体积为V2
初状态
p1=2.0×106 Pa,V1=10 L
末状态
p2=1.0×105 Pa,V2=?
由玻意耳定律得
p1V1=p2V2
解得
V2==200 L
因此
即容器里剩下的气体是原来的5%。
24.85 cmHg;5 cm
【详解】
设玻璃管的横截面积为S,水银的密度为ρ,初态时,管内气体的温度为
T1=306 K
体积为
V1=51 cm·S
压强为
p1=p0+ρgh=80 cmHg.
当水银面与管口相平时,设水银柱高度为H,则管内气体的体积为
V2=(l-H)S
压强为
p2=p0+ρgH
由玻意耳定律得
p1V1=p2V2
联立解得
H=9 cm(H=-28 cm不合题意,舍去)
所以
p2=85 cmHg
新注入水银柱的高度为
Δh=H-4 cm=5cm
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图所示,一端封闭的玻璃管,开口向下竖直插在水银槽里,管内封有长度分别为l1和l2的两段理想气体。外界温度和大气压均不变,当将管慢慢地向上提起时,管内气柱的长度( )
A.l1变小,l2变大 B.l1变大,l2变小
C.l1、l2都变小 D.l1、l2都变大
2.下列不是描述气体状态参量的物理量是( )
A.压强 B.体积
C.质量 D.温度
3.如图所示为某同学设计的喷药装置,内部装有8L药液,上部密封1atm的空气1L,保持阀门关闭,再充入1atm的空气0.2L,设在所有过程中空气可看成理想气体,且温度不变,下列说法错误的是( )
A.充气后,密封气体的压强增大为1.2atm
B.充气后,密封气体的分子平均动能不变
C.打开阀门后,密封气体对外界做正功
D.打开阀门后,不再充气也能把药液喷光
4.如图是一竖直放置开口向上的均匀玻璃管,内用水银柱封有一定质量的理想气体,水银与玻璃管间摩擦力不计,开始时手拿玻璃管处于平衡状态,后松开手,玻璃管沿竖直方向运动,最后达到稳定状态的过程中,下列说法中正确的是 ( )
A.刚开始瞬间,玻璃管的加速度一定大于重力加速度g
B.刚开始短时间内,试管内的气体压强一定在逐渐变小
C.刚开始短时间内,玻璃管的加速度在逐渐变小
D.以上情况一定均会发生
5.一个气泡从水面下深处缓缓上升到水面,假定水的温度均匀,水面上方的压强为,则气泡到达水面时的体积为原来的( )
A.3倍 B.4倍 C.5倍 D.6倍
6.现有一个容积为400L的医用氧气罐,内部气体可视为理想气体,压强为15MPa,为了使用方便,用一批相同规格的小型氧气瓶(瓶内视为真空)进行分装,发现恰好能装满40个小氧气瓶,分装完成后原医用氧气罐及每个小氧气瓶内气体的压强均为3MPa,不考虑分装过程中温度的变化,则每个小氧气瓶的容积为( )
A.20L B.40L C.50L D.60L
7.医用氧气钢瓶的容积,室内常温下充装氧气后,氧气钢瓶内部压强,释放氧气时瓶内压强不能低于。病人一般在室内常温下吸氧时,每分钟需要消耗下氧气,室内常温下,一瓶氧气能供一个病人吸氧的最长时间为( )
A.23小时 B.33.5小时 C.46小时 D.80小时
8.如图,两端开口的弯管,左管插入水银槽中,右管有一小段水银柱,中间封有一段空气。能使得左管内部水银面相对水银槽上升的操作是( )
A.环境温度降低少许 B.把弯管向右侧倾斜一点
C.把弯管竖直向上提一点 D.把弯管竖直向下压一点
9.在两端开口的弯管中用两段水银柱封闭了一段空气柱,如图所示,若再往a管内注入少量水银,则( )
A.a、b水银面高度差将减小
B.a、b水银面高度差将大于c、d水银面高度差
C.b管水面上升的距离等于c管水面下降的距离
D.b管水面上升的距离大于c管水面下降的距离
10.血压仪由加压气囊、臂带,压强计等构成,如图所示。加压气囊可将外界空气充入臂带,压强计示数为臂带内气体的压强高于大气压强的数值,充气前臂带内气体压强为大气压强,体积为V;每次挤压气囊都能将的外界空气充入臂带中,经5次充气后,臂带内气体体积变为,压强计示数为。已知大气压强等于,气体温度不变。忽略细管和压强计内的气体体积。则V等于( )
A. B. C. D.
11.如图所示,粗细均匀竖直放置的玻璃管中,P为一小活塞,有一段水银柱将封闭在玻璃管中的空气分成上、下两部分,活塞和水银柱都静止不动。现在用力向下压活塞,使得活塞向下移动一段距离L,同时水银柱将向下缓慢移动一段距离H,在此过程中温度不变,则有( )
A.L>H B.L
A.调节空气柱长度后立刻读数
B.拉上窗帘防止阳光直射玻璃管
C.推拉活塞时,为了防止手滑应该用手紧握玻璃管
D.实验中若密封橡胶帽脱落,应立刻堵住后继续实验
13.活塞式真空泵的工作原理如图,抽气筒与被抽密闭容器通过自动阀门相连,当活塞从抽气筒的左端向右移动到右端过程中,阀门自动开启,密闭容器内的气体流入抽气筒,活塞从右端向左移动到左端过程中,阀门自动关闭,抽气筒内活塞左侧的气体被排出,即完成一次抽气过程,如此往复,密闭容器内的气体压强越来越小。若密闭容器的容积为V,抽气筒的容积为0.1V,抽气前密闭容器内气体的压强为p0。抽气过程中气体的温度不变,若第1次抽气过程中被抽出的气体质量为m1,第2次抽气过程中被抽出的气体质量为m2,则m2∶m1为( )
A.1 B.0.9∶1.1 C.1∶1.1 D.1∶1.12
14.如图所示,,、三根完全相同的玻璃管,一端封闭,管内各用相同长度的一段水银柱封闭了质量相等的空气,管竖直向下做自由落体运动,管竖直向上做加速度为的匀加速运动,管沿倾角为的光滑斜面下滑,若空气温度始终相同且不变,当水银柱相对管壁静止时,,、三管内的空气柱长度、、间的关系为( )
A. B. C. D.
15.容积V=10L的钢瓶充满氧后,压强p=20atm,打开钢瓶盖阀门,让氧气分别装到容积为V0=5L的小瓶子中去,若小瓶子已抽成真空,分装到小瓶子中的氧气压强均为p0=2atm。在分装过程中无漏气现象,且温度保持不变,那么最多可装的瓶数是( )
A.2瓶 B.18瓶 C.0.10瓶 D.20瓶
二、填空题
16.一内壁光滑、粗细均匀的U形玻璃管竖直放置,左端开口,右端封闭,左端上部有一轻活塞。初始时,管内水银柱及空气柱长度如图所示。已知大气压强p0=75cmHg,环境温度不变。右侧封闭气体的压强p右=______cmHg;为使管内两边水银柱高度相等并达到稳定,需要用力向下缓慢推活塞______cm。
17.如图所示,在p-V图中,1、2、3三个点代表某容器中一定质量理想气体的三个不同状态,对应的温度分别是T1、T2、T3。用N1、N2、N3分别表示这三个状态下气体分子在单位时间内撞击容器壁上单位面积的次数,用n1、n2、n3分别表示这三个状态下单位体积内的气体分子数,则T1______T3,n2______n3。(填“>”、“=”或“<”)
18.已知地球大气层的厚度h远小于地球半径R,空气平均摩尔质量为M,阿伏加德罗常数为NA,大气层中空气的总质量为m,重力加速度为g.可以估算出地球大气层空气分子总数为_____________,地面大气压强为______________.
19.如图所示,粗细均匀的竖直倒置的U形管右端封闭,左端开口插入水银槽中,封闭着两段空气柱1和2,已知,,外界大气压强为75cmHg,则空气柱1的压强为___________空气柱2的压强为___________。
三、解答题
20.若已知大气压强为p0,图中各装置均处于静止状态,液体密度均为ρ,重力加速度为g,求各被封闭气体的压强。
21.随着社会工业化的发展,对环境的污染越来越严重,尤其是对居民日常饮用水的污染也不可小觑,因此经过特殊工艺处理的桶装水也就走进了千家万户。如图甲是一种桶装水手压式压水器,按压手压头,能够把一定量的外界空气压入密闭水桶内,水从出水管流出,如图乙是简化的原理图,初始时桶内的空气体积为,出水管竖直部分内外液面相平,出水口与桶内水面的高度差为,压水器气囊的容积,水桶的横截面积为。空气可视为理想气体,出水管内水的体积可忽略不计,水的密度,外界大气压强,取。
(ⅰ)若环境温度不变,假若第一次按压后,水没有流出,求此时桶内空气的压强;
(ⅱ)若环境温度不变,按压出了1.0L水,求压入的外界空气的体积。
22.如图,两个相同的内壁光滑的薄壁汽缸和,质量均为,用质量均为的活塞封闭同种气体,体积都为,汽缸的开口处有卡环可以防止活塞离开汽缸。活塞跟汽缸的缸底用细线相连后跨过滑轮,斜面光滑,倾角为。已知大气对活塞的压力等于活塞重力的2.25倍,且,重力加速度为。在外力的作用下,系统一开始处于静止状态,细线绷紧。现撤去外力,让和一起运动,待系统稳定后,求
(1)和运动的加速度大小;
(2)若汽缸中温度不变,汽缸中气体体积变为多少?
23.某个容器的容积是10 L,所装气体的压强是2.0×106 Pa、如果温度保持不变,把容器的开关打开以后,容器里剩下的气体是原来的百分之几?(设大气压是1.0×105 Pa)
24.如图所示,在长为l=57 cm、一端封闭且另一端开口向上的竖直玻璃管内,用4 cm高的水银柱封闭着51 cm长的理想气体,管内外气体的温度均为33 ℃.现将水银缓慢注入管中,直到水银面与管口相平.此时管中气体的压强为多少?新注入水银柱的高度为多少?(大气压强为p0=76 cmHg)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【详解】
当将管慢慢地向上提起时,假设上段空气柱长度不变,则下段空气柱体积增大,由玻意耳定律可知压强减小,从而导致上段气体压强减小,因此上段气体体积增大,故l1、l2都变大,故ABC错误,D正确。
故选D。
2.C
【详解】
描述气体的状态参量,有压强、体积、温度。
故选C。
3.D
【详解】
A.把充入的气体和原气体作为整体:气体做等温变化,根据玻意耳定律可得
解得
故A正确,不符合题意;
B.温度是平均动能的标志,温度不变,所以分子的平均动能不变,故B正确,不符合题意;
C.充气后封闭气体压强变为1.2atm,大于大气压强,所以打开阀门后,气体膨胀,对外界做功,故C正确,不符合题意;
D.膨胀过程温度不变属于等温变化,若都喷完容器中的水,由
得喷完容器中的水后,容器的气体压强小于外界气体压强,所以水不能喷完,故D错误,符合题意。
故选D。
4.D
【详解】
一开始玻璃管处于平衡状态,放手后,玻璃管可能速度向上,或者向下,或者为零。刚开始运动时,玻璃管的内部气体的压强大于外部,所以玻璃管的加速度大于重力加速度g;最初水银所受合力为零,当玻璃管向下或向下运动后,内部气体压强减小,内外气体压强差减少,所以最初的短时间内,水银的加速度在逐渐变大,玻璃管的加速度逐渐变逐渐变小。
故选D。
5.C
【详解】
气泡在水面下40m深处的压强为
根据玻意耳定律,可得
解得
故选C。
6.B
【详解】
设每个小氧气瓶的容积为V0,以医用氧气罐中所有氧气为研究对象,初态:p1=15MPa,V1=400L;末态:p2=3MPa,V2=40V0+400L;因为不考虑温度变化,由玻意耳定律有
代入数据得V0=40L,B正确。
故选B。
7.C
【详解】
由题意可知,气体的温度不变,由玻意耳定律可得
解得
一瓶氧气能供一个病人吸氧的最长时间为
故C正确,ABD错误。
故选C。
8.B
【详解】
左管内水银面相对水银槽内的水银的高度差等于右管中水银柱的高度h,则要使得左管内部水银面相对水银槽上升,则必须要减小h,可把弯管向右侧倾斜一点,将水银柱的竖直高度减小。另外三个方法均不能使左管内部水银面相对水银槽上升。
故选B。
9.D
【详解】
AB.向a管注入水后,封闭气体压强变大,气体体积减小,a、b两液面高度差以及c、d液面高度差都变大;由p=p0+h可知ab水银面高度差等于cd水银面高度差,故AB错误;
CD.向a管注入水后,b管水银面上升,c管水银面下降,因封闭气体压强变大,气体体积减小,所以b管水面上升的距离大于c管水面下降的距离,故C错误,D正确。
故选D。
10.D
【详解】
根据玻意耳定律可知
已知
,,
代入数据整理得
故选D。
11.A
【详解】
题目没说压力多大,可以采用极限法分析,不妨设其为无穷大,这时空气柱的体积几乎都被压缩为零。显然,活塞移动的距离要比水银柱移动的距离多A部分空气柱的长度,即L比H大。
故选A。
【点睛】
在单调函数的变化过程中,可以应用极限法定性分析物理量之间的变化关系。例如,本题中,压强与体积之间的变化关系是减函数,可以采用极限法分析当压强为无穷大时对应的体积情况;活塞移动距离与气体体积减小量之间的变化关系是增函数,可以采用极限法分析当体积为零时对应的活塞移动的距离。
12.B
【详解】
A.调节空气柱长度的过程中,外界对气体做功,气体温度发生变化,为保持气体温度不变,调节空气柱长度后不要立即读数,要等气体状态稳定后再读数,故A错误;
B.实验过程要保持气体温度不变,拉上窗帘防止阳光直射玻璃管,所以B正确;
C.当用手直接握在注射器上时,手的温度可能改变气体的温度,所以不要用手直接握在注射器上,则C错误;
D.实验时要保持气体的质量不变,实验中若密封橡胶帽脱落,注射器内气体的质量发生变化,则不能继续实验,所以D错误;
故选B。
13.C
【详解】
根据玻意耳定律,第1次抽气过程
第2次抽气过程
而正比于,正比于,所以
故选C。
14.D
【详解】
设大气压为。对管,管竖直向下做自由落体运动,处于完全失重状态,封闭气体的压强等于大气压,即。
对管,以水银为研究对象,根据牛顿第二定律得
得
对管,以水银为研究对象,根据牛顿第二定律得
对管和水银整体,有
得
解得
可得
根据玻意耳定律有,可得,ABC错误,D正确。
故选D。
15.B
【详解】
由玻意耳定律得
pV=p1V1
即
20atm×10L=2atm×V1
解得
V1=100L
最多可装的瓶数是
瓶
故选B。
16. 90 9.417
【详解】
[1]
[2]两边水银柱一样高,则左边下降右边上升各7.5cm。所以右边被封气体高度变为12.5cm,对右边气体,由玻意耳定律:
此时左侧气体压强也为p2。
对于左侧气体,由玻意耳定律:
所以活塞下降距离为:
17. = >
【详解】
[1]由于在1、3两状态下,有
则T1= T3。
[2]根据题图可知,2状态的体积小于3状态的体积,又气体分子总数不变,有n2>n3。
18.
【详解】
[1]地球大气层空气分子总数为,
[2]大气压强由于重力作用产生,即有 ;
19. 60cmHg 72cmHg
【详解】
[1]以气柱1作为研究对象有
p1=p0-ph1=60cmHg
[2]以气柱2作为研究对象有
pB=p1+ph2=72cmHg
20.甲:;乙:;丙:;丁:;戊:,
【详解】
题图甲中,以高为h的液柱为研究对象,由平衡条件知
解得
题图乙中,以B液面为研究对象,由平衡条件知
解得
题图丙中,以B液面为研究对象,由平衡条件有
解得
题图丁中,以A液面为研究对象,由平衡条件得
所以
题图戊中,从开口端开始计算,右端大气压强为p0,同种液体同一水平面上的压强相同,
所以b气柱的压强为
故a气柱的压强为
21.(ⅰ);(ⅱ)
【详解】
(ⅰ)设此时桶内空气的压强为p,由理想气体状态方程得
解得
(ⅱ)设流出水后,液面下降的高度为,则
此时桶中空气的压强
体积
设桶中空气在压强时的体积为,由玻意耳定律得
压入的外界空气的体积
解得
22.(1);(2)
【详解】
(1)当系统处于光滑斜面时,对系统分析,则有
解得
(2)系统均静止时,对中活塞分析,则有
解得
加速运动时对中活塞,则有
解得
由玻意耳定律,则有
解得
23.5%
【详解】
以原来气体为研究对象,设原来的气体体积为V1,膨胀后气体的体积为V2
初状态
p1=2.0×106 Pa,V1=10 L
末状态
p2=1.0×105 Pa,V2=?
由玻意耳定律得
p1V1=p2V2
解得
V2==200 L
因此
即容器里剩下的气体是原来的5%。
24.85 cmHg;5 cm
【详解】
设玻璃管的横截面积为S,水银的密度为ρ,初态时,管内气体的温度为
T1=306 K
体积为
V1=51 cm·S
压强为
p1=p0+ρgh=80 cmHg.
当水银面与管口相平时,设水银柱高度为H,则管内气体的体积为
V2=(l-H)S
压强为
p2=p0+ρgH
由玻意耳定律得
p1V1=p2V2
联立解得
H=9 cm(H=-28 cm不合题意,舍去)
所以
p2=85 cmHg
新注入水银柱的高度为
Δh=H-4 cm=5cm
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 分子动理论
- 第一节 物质是由大量分子组成的
- 第二节 分子热运动与分子力
- 第三节 气体分子运动的统计规律
- 第二章 气体、液体和固态
- 第一节 气体实验定律(Ⅰ)
- 第二节 气体实验定律(Ⅱ)
- 第三节 气体实验定律的微观解释
- 第四节 液体的表面张力
- 第五节 晶体
- 第六节 新材料
- 第三章 热力学定律
- 第一节 热力学第一定律
- 第二节 能量守恒定律及其应用
- 第三节 热力学第二定律
- 第四章 波粒二象性
- 第一节 光电效应
- 第二节 光电效应方程及其意义
- 第三节 光的波粒二象性
- 第四节 德布罗意波
- 第五节 不确定性关系
- 第五章 原子与原子核
- 第一节 原子的结构
- 第二节 放射性元素的衰变
- 第三节 核力与核反应方程
- 第四节 放射性同位素
- 第五节 裂变和聚变
