人教版七年级下册第六章 实数6.2 立方根 课件(共24张PPT)
文档属性
| 名称 | 人教版七年级下册第六章 实数6.2 立方根 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-06 16:20:06 | ||
图片预览





文档简介
(共24张PPT)
【义务教育教科书人教版七年级下册】
6.2 立方根
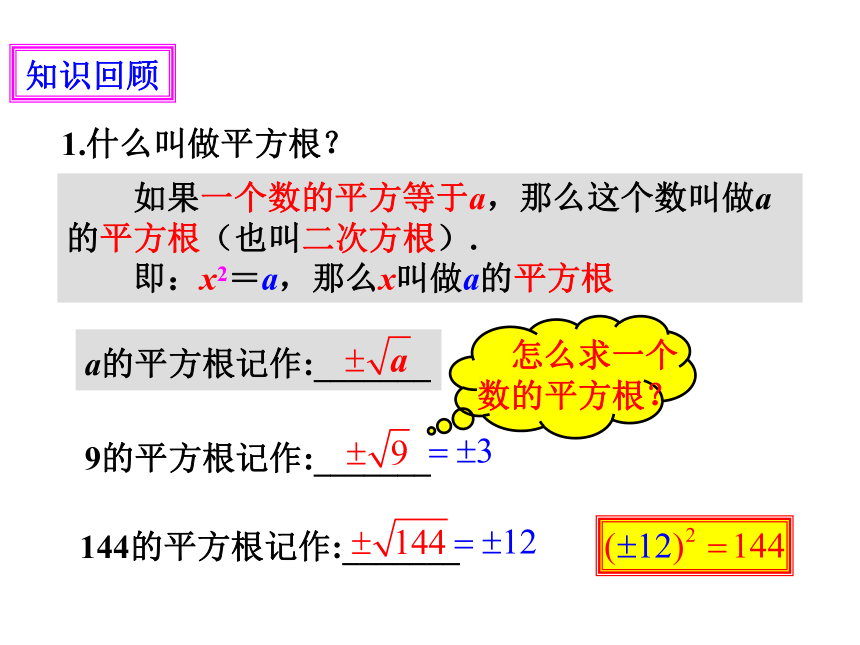
知识回顾
1.什么叫做平方根?
如果一个数的平方等于a,那么这个数叫做a的平方根(也叫二次方根).
即:x2=a,那么x叫做a的平方根
a的平方根记作:_______
144的平方根记作:_______
9的平方根记作:_______
怎么求一个数的平方根?
知识回顾
填空:
(1)2的平方根是________;
(2)0的平方根是________;
(3)-16的平方根是____________.
正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
0
没有平方根
平方根具有什么性质呢?
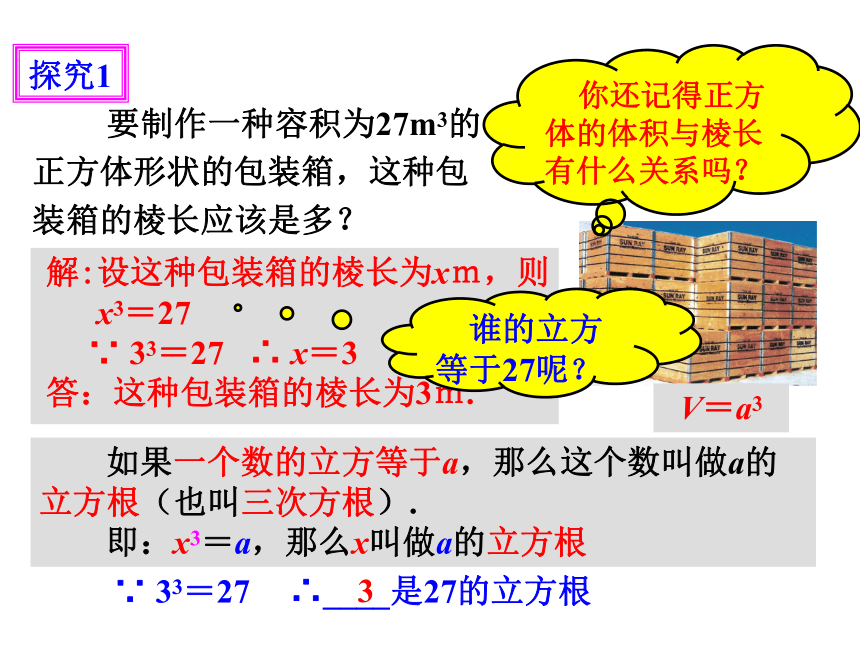
探究1
要制作一种容积为27m3的正方体形状的包装箱,这种包装箱的棱长应该是多?
解:设这种包装箱的棱长为xm,则
x3=27
∵ 33=27 ∴ x=3
答:这种包装箱的棱长为3m.
你还记得正方体的体积与棱长有什么关系吗?
V=a3
谁的立方等于27呢?
如果一个数的立方等于a,那么这个数叫做a的立方根(也叫三次方根).
即:x3=a,那么x叫做a的立方根
∵ 33=27
∴____是27的立方根
3
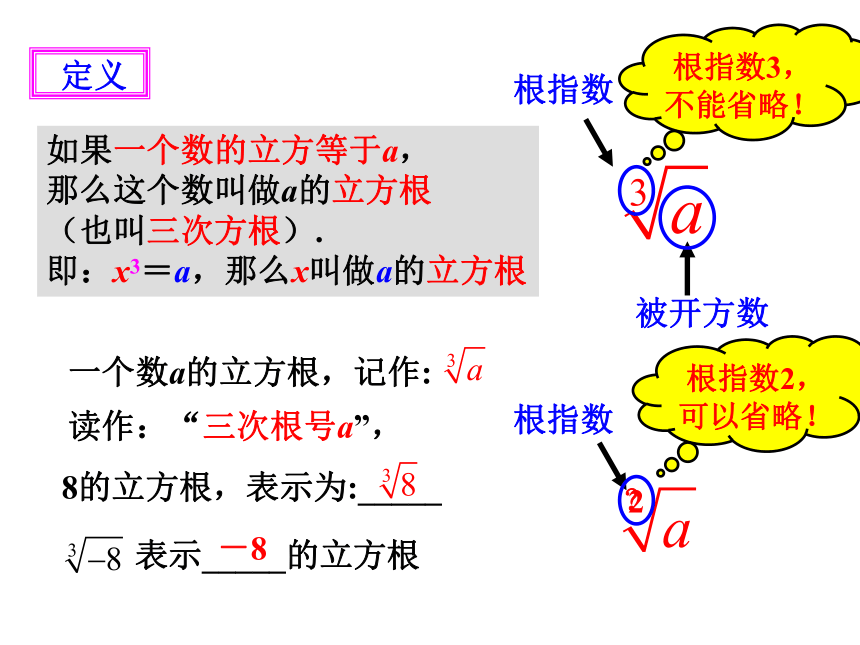
定义
一个数a的立方根,记作:
读作:“三次根号a”,
被开方数
根指数
根指数3,不能省略!
8的立方根,表示为:_____
表示_____的立方根
-8
根指数
?
2
根指数2,可以省略!
如果一个数的立方等于a,
那么这个数叫做a的立方根
(也叫三次方根).
即:x3=a,那么x叫做a的立方根
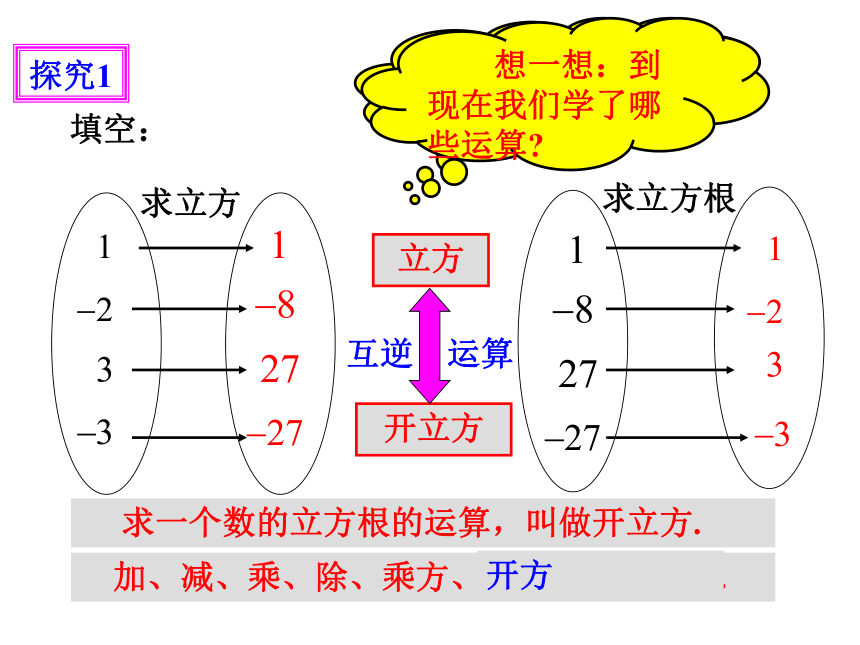
探究1
填空:
求立方
求立方根
左右两图中的运算有什么关系?
立方
开立方
互逆 运算
求一个数的立方根的运算,叫做开立方.
想一想:到现在我们学了哪些运算
加、减、乘、除、乘方、开平方、开立方.
开方
练习1
求下列各数的立方根:
解:(1)∵(-3)3=-27
∴ -27的立方根是-3
(2)∵( )3=
∴ 的立方根是
(3)∵(-4)3=-64
∴ -64的立方根是-4
探究2
根据立方根的意义填空.
你能发现正数、0和负数的立方根各有什么特点吗?
∵( )3 =8, ∴8的立方根是( );
∵( )3 =0.064 , ∴ 0.064的立方根是( );
∵( )3 = 0, ∴ 0的立方根是( );
∵( )3 =-8 , ∴ -8的立方根是( );
∵( )3 = , ∴ 的立方根是( ).
2
2
0.4
0.4
0
0
-2
-2
立方根的性质
(1)正数的立方根是正数;
(2)负数的立方根是负数;
(3) 0的立方根是0.
探究2
思考:你能归纳出平方根和立方根的异同点吗
被开方数 平方根 立方根
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
练习2
判断下列说法是否正确, 并说明理由.
(2) 25的平方根是5 ( )
(3) -64没有立方根( )
(4) -4的平方根是±2( )
(5) 0的平方根和立方根都是0 ( )
0,±1
(1)
的立方根是
( )
×
×
×
×
√
立方根是它本身的数有那些
算术平方根是它本身的数有那些
0,1
一般地, .
探究3
填空,你能发现其中的规律吗?
因为 = ,
所以
因为
所以
-2
=
=
-2
-3
-3
应用
例:求下列各式的值 :
解:
练习3
求下列各式的值 :
解:
探究4
用计算器求下列各式的值: (1) ;(2) (精确到0.001).
解:(1) 依次按键 、 8 、 ,
显示:2.
∴ .
(2) 依次按键 、1845、 ,
显示:12.264 940 81.
∴ .
有些计算器要用到第二功能键来求一个数的立方根.
8
探究4
利用计算器计算,并将计算结果填在表中,你发现了什么规律?
规律:被开方数的小数点向右(或向左)移动3位,其立方根的小数点向右(或向左)移动1位.
…
…
…
…
0.06
0.6
6
60
你能用计算器计算 (精确到0.001)吗?并利用刚才的得到规律说出 , , 的近似值.
想一想: 你能否根据 的值说出 是多少?
解:
答:不能
探究4
应用提高
1. 你能比较3,4, 的大小吗?
解:∵33=27,
∴
∵ 43=64 ,
∴
∵
∴
被开方数越大,对应的立方根也越大.
应用提高
2. 求下列各式中的 x:
(1)9x3+72=0; (2)2(x-1)3=54.
解: (1) 9x3+72=0
9x3=-72
x3=-8
∵(-2)3=-8
∴x=-2
(2) 2(x-1)3=54
(x-1)3=27
∵33=27
∴x-1=3
x=4
今天我们学习了哪些知识?
1.什么是立方根?
2.如何求一个数的立方根?
3.立方根有什么性质?
体验收获
达标测评
1. 8的立方根是( )
A.2 B.±2 C.4 D. ±4
A
2. 的绝对值是( )
A.-27 B. 27 C.-3 D. 3
D
3. 1的平方根是_______;1立方根是_______.
1
±1
4.
-2
达标测评
5. 现在要做一个体积为64cm3的立方体魔方,它的棱长要取多长?
解:设魔方的棱长为xcm, 则
答:这个魔方的棱长为4cm.
x3=64
x=4
达标测评
6. 比较下列各组数的大小.
(1) 与2.5; (2) 与 .
解: (1) ∵9 < 2.53,
∴ <2.5
(2) ∵ 4> ,
∴ >
布置作业
教材52页习题6.2第3、5题.
【义务教育教科书人教版七年级下册】
6.2 立方根
知识回顾
1.什么叫做平方根?
如果一个数的平方等于a,那么这个数叫做a的平方根(也叫二次方根).
即:x2=a,那么x叫做a的平方根
a的平方根记作:_______
144的平方根记作:_______
9的平方根记作:_______
怎么求一个数的平方根?
知识回顾
填空:
(1)2的平方根是________;
(2)0的平方根是________;
(3)-16的平方根是____________.
正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
0
没有平方根
平方根具有什么性质呢?
探究1
要制作一种容积为27m3的正方体形状的包装箱,这种包装箱的棱长应该是多?
解:设这种包装箱的棱长为xm,则
x3=27
∵ 33=27 ∴ x=3
答:这种包装箱的棱长为3m.
你还记得正方体的体积与棱长有什么关系吗?
V=a3
谁的立方等于27呢?
如果一个数的立方等于a,那么这个数叫做a的立方根(也叫三次方根).
即:x3=a,那么x叫做a的立方根
∵ 33=27
∴____是27的立方根
3
定义
一个数a的立方根,记作:
读作:“三次根号a”,
被开方数
根指数
根指数3,不能省略!
8的立方根,表示为:_____
表示_____的立方根
-8
根指数
?
2
根指数2,可以省略!
如果一个数的立方等于a,
那么这个数叫做a的立方根
(也叫三次方根).
即:x3=a,那么x叫做a的立方根
探究1
填空:
求立方
求立方根
左右两图中的运算有什么关系?
立方
开立方
互逆 运算
求一个数的立方根的运算,叫做开立方.
想一想:到现在我们学了哪些运算
加、减、乘、除、乘方、开平方、开立方.
开方
练习1
求下列各数的立方根:
解:(1)∵(-3)3=-27
∴ -27的立方根是-3
(2)∵( )3=
∴ 的立方根是
(3)∵(-4)3=-64
∴ -64的立方根是-4
探究2
根据立方根的意义填空.
你能发现正数、0和负数的立方根各有什么特点吗?
∵( )3 =8, ∴8的立方根是( );
∵( )3 =0.064 , ∴ 0.064的立方根是( );
∵( )3 = 0, ∴ 0的立方根是( );
∵( )3 =-8 , ∴ -8的立方根是( );
∵( )3 = , ∴ 的立方根是( ).
2
2
0.4
0.4
0
0
-2
-2
立方根的性质
(1)正数的立方根是正数;
(2)负数的立方根是负数;
(3) 0的立方根是0.
探究2
思考:你能归纳出平方根和立方根的异同点吗
被开方数 平方根 立方根
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
练习2
判断下列说法是否正确, 并说明理由.
(2) 25的平方根是5 ( )
(3) -64没有立方根( )
(4) -4的平方根是±2( )
(5) 0的平方根和立方根都是0 ( )
0,±1
(1)
的立方根是
( )
×
×
×
×
√
立方根是它本身的数有那些
算术平方根是它本身的数有那些
0,1
一般地, .
探究3
填空,你能发现其中的规律吗?
因为 = ,
所以
因为
所以
-2
=
=
-2
-3
-3
应用
例:求下列各式的值 :
解:
练习3
求下列各式的值 :
解:
探究4
用计算器求下列各式的值: (1) ;(2) (精确到0.001).
解:(1) 依次按键 、 8 、 ,
显示:2.
∴ .
(2) 依次按键 、1845、 ,
显示:12.264 940 81.
∴ .
有些计算器要用到第二功能键来求一个数的立方根.
8
探究4
利用计算器计算,并将计算结果填在表中,你发现了什么规律?
规律:被开方数的小数点向右(或向左)移动3位,其立方根的小数点向右(或向左)移动1位.
…
…
…
…
0.06
0.6
6
60
你能用计算器计算 (精确到0.001)吗?并利用刚才的得到规律说出 , , 的近似值.
想一想: 你能否根据 的值说出 是多少?
解:
答:不能
探究4
应用提高
1. 你能比较3,4, 的大小吗?
解:∵33=27,
∴
∵ 43=64 ,
∴
∵
∴
被开方数越大,对应的立方根也越大.
应用提高
2. 求下列各式中的 x:
(1)9x3+72=0; (2)2(x-1)3=54.
解: (1) 9x3+72=0
9x3=-72
x3=-8
∵(-2)3=-8
∴x=-2
(2) 2(x-1)3=54
(x-1)3=27
∵33=27
∴x-1=3
x=4
今天我们学习了哪些知识?
1.什么是立方根?
2.如何求一个数的立方根?
3.立方根有什么性质?
体验收获
达标测评
1. 8的立方根是( )
A.2 B.±2 C.4 D. ±4
A
2. 的绝对值是( )
A.-27 B. 27 C.-3 D. 3
D
3. 1的平方根是_______;1立方根是_______.
1
±1
4.
-2
达标测评
5. 现在要做一个体积为64cm3的立方体魔方,它的棱长要取多长?
解:设魔方的棱长为xcm, 则
答:这个魔方的棱长为4cm.
x3=64
x=4
达标测评
6. 比较下列各组数的大小.
(1) 与2.5; (2) 与 .
解: (1) ∵9 < 2.53,
∴ <2.5
(2) ∵ 4> ,
∴ >
布置作业
教材52页习题6.2第3、5题.
