人教版数学七下 6.3 实数 课件(共28张PPT)
文档属性
| 名称 | 人教版数学七下 6.3 实数 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-06 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
【义务教育教科书人教版七年级下册】
6.3 实数
有理数
整数
分数
有理数
正有理数
零
负有理数
回顾
有理数包括哪些数?
3,
,
3
5
,
47
8
,
11
9
,
11
9
.
5
9
像
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
3 = 3.0,
= 0.6,
3
5
47
8
= 5.875,
11
9
= 0.81,
.
.
= 0.5.
5
9
.
= 1.2,
11
9
.
★任何一个有理数都可以写成有限小数或无限循环小数的形式.
探究1
知识回顾
1、把两个边长为1小正方形沿对角线剪开,将所得的4个直角三角形如图拼在一起,就得到一个面积为2的大正方形,于是可得大正方形的边长为
你知道边长为1的小正方形,对角线长为多少吗
2、面积为3的正方形的边长为
叫做无理数.
=1.41421356237309504880168…
=1.73205080756887729352744…
… …
π=3.1415926535897932384626…
1.010010001…
(两个1之间依次多一个0)
无限不循环小数
一、无理数的概念
根据你所看到的或想到的,你觉得无理数都有哪些特征?
试一试
把下列各数分别填入相应的集合内:
0.101,
,
有理数
无理数
集合
集合
...
...
1.圆周率 及一些含有 的数
2.开不尽方的数
3.有一定的规律,但
不循环的无限小数
无理数的特征:
注意:带根号的数不一定是无理数
二、实数的概念
有理数和无理数统称实数.
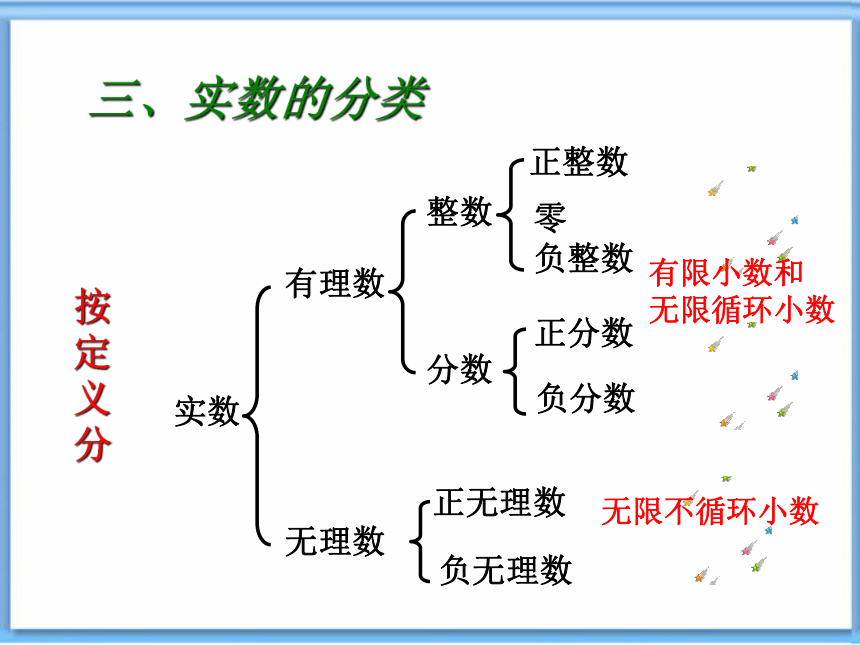
三、实数的分类
实数
有理数
无理数
整数
分数
正无理数
负无理数
正整数
零
负整数
正分数
负分数
按定义分
有限小数和
无限循环小数
无限不循环小数
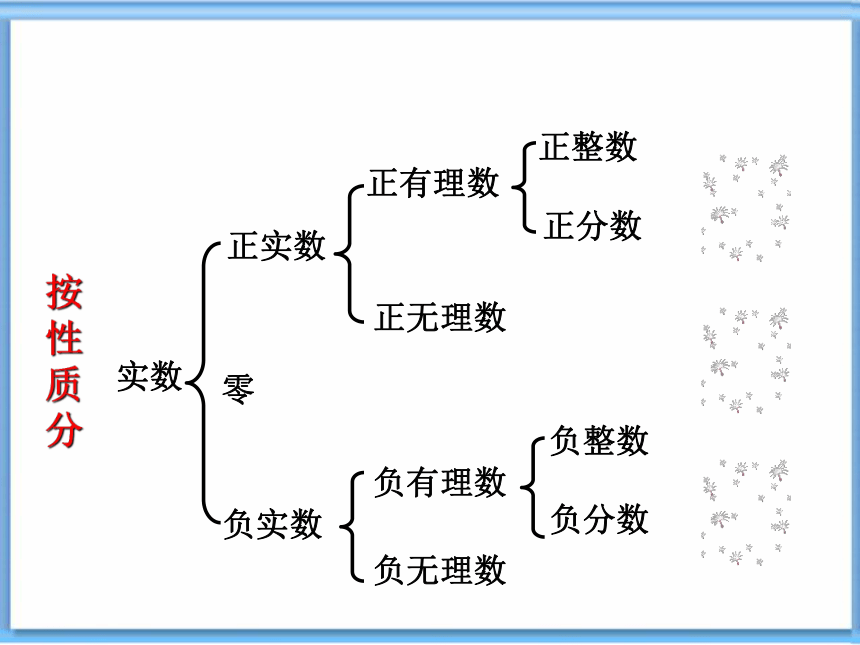
实数
正实数
负实数
正有理数
正无理数
负有理数
负无理数
正整数
零
负整数
正分数
负分数
按性质分
练一练
1.判断:
(1)实数不是有理数就是无理数;( )
(2)无理数都是无限不循环小数;( )
(3)无理数都是无限小数; ( )
(4)带根号的数都是无理数; ( )
(5)无理数一定都带根号. ( )
×
×
探究2
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达O’点,则点O’的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
O’
0
1
2
4
3
-1
-2
探究3:你能在数轴上表示 和 吗?
每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
四、实数与数轴上的点的对应关系
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数。
★实数和数轴上的点是一一对应的.
随堂练习(P56-1)
解:点A表示-1.5;
点B表示 ;
点C表示 ;
点D表示3;
点E表示 .
思考:
有理数关于相反数和绝对值,
对实数是否有意义?
五、在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
相反数:
实数 a 的相反数是- a.若a与b互为相反数,则a+b=0.
绝对值:
实数a的绝对值,记为|a|,它是一个非负实数.
|a| =
a( a﹥0 )
0 ( a = 0)
-a( a﹤0)
几何意义: |a|表示点x到原点0的距离.而| a-b |表示点a与点b的距离.
倒数:
乘积是1的两个数互为倒数.若a与b互为倒数,则ab=1.
如果 a ≠ 0 ,那么它的倒数为 .
(1)分别写出- , 的相反数;
(3)求
(4)已知一个数的绝对值是
求这个数.
练习、填空:
(1) 的相反数是__________
(5) 绝对值是 _________
(2) 的倒数是__
(3)| | =___________
(4)绝对值等于 的数是 _________
的平方 是___
(6) 比较大小:-7
当数从有理数扩充到实数以后,实数之间不仅可以进行加 减 乘 除 乘方运算,又增加了非负数的开平方运算,任意实数可以进行开立方运算。进行实数运算时,有理数的运算法则及性质等同样适用。
【规律方法】实数运算的“三个关键”:
1. 运算法则:乘方和开方运算、幂的运算、指数(特别是负整数指数,0指数)运算、根式运算、特殊三角函数值的计算以及绝对值的化简等.
2. 运算顺序:先乘方,再乘除,后加减,有括号的先算括号里面的,在同一级运算中要从左到右依次运算,无论何种运算,都要注意先定符号后运算.
3. 运算律的使用:使用运算律可以简化运算,提高运算速度和准确度.
例2 计算下列各式的值
练习:
1.
2.
3.
4.
例3计算(结果保留小数点后两位)
巩固练习(一)
1.下列各数不是有理数的是( )
A.3.14 B.-π C.
D.
2.在
中是无理数的有( )
A. 2 个 B.3个 C.4个 D.1个
B
A
巩固练习(二)
(2)若
(3)
巩固练习(三)
再见!
【义务教育教科书人教版七年级下册】
6.3 实数
有理数
整数
分数
有理数
正有理数
零
负有理数
回顾
有理数包括哪些数?
3,
,
3
5
,
47
8
,
11
9
,
11
9
.
5
9
像
使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
3 = 3.0,
= 0.6,
3
5
47
8
= 5.875,
11
9
= 0.81,
.
.
= 0.5.
5
9
.
= 1.2,
11
9
.
★任何一个有理数都可以写成有限小数或无限循环小数的形式.
探究1
知识回顾
1、把两个边长为1小正方形沿对角线剪开,将所得的4个直角三角形如图拼在一起,就得到一个面积为2的大正方形,于是可得大正方形的边长为
你知道边长为1的小正方形,对角线长为多少吗
2、面积为3的正方形的边长为
叫做无理数.
=1.41421356237309504880168…
=1.73205080756887729352744…
… …
π=3.1415926535897932384626…
1.010010001…
(两个1之间依次多一个0)
无限不循环小数
一、无理数的概念
根据你所看到的或想到的,你觉得无理数都有哪些特征?
试一试
把下列各数分别填入相应的集合内:
0.101,
,
有理数
无理数
集合
集合
...
...
1.圆周率 及一些含有 的数
2.开不尽方的数
3.有一定的规律,但
不循环的无限小数
无理数的特征:
注意:带根号的数不一定是无理数
二、实数的概念
有理数和无理数统称实数.
三、实数的分类
实数
有理数
无理数
整数
分数
正无理数
负无理数
正整数
零
负整数
正分数
负分数
按定义分
有限小数和
无限循环小数
无限不循环小数
实数
正实数
负实数
正有理数
正无理数
负有理数
负无理数
正整数
零
负整数
正分数
负分数
按性质分
练一练
1.判断:
(1)实数不是有理数就是无理数;( )
(2)无理数都是无限不循环小数;( )
(3)无理数都是无限小数; ( )
(4)带根号的数都是无理数; ( )
(5)无理数一定都带根号. ( )
×
×
探究2
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达O’点,则点O’的坐标为多少?
-4
-2
0
1
2
3
4
-1
-3
O’
0
1
2
4
3
-1
-2
探究3:你能在数轴上表示 和 吗?
每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
四、实数与数轴上的点的对应关系
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数。
★实数和数轴上的点是一一对应的.
随堂练习(P56-1)
解:点A表示-1.5;
点B表示 ;
点C表示 ;
点D表示3;
点E表示 .
思考:
有理数关于相反数和绝对值,
对实数是否有意义?
五、在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
相反数:
实数 a 的相反数是- a.若a与b互为相反数,则a+b=0.
绝对值:
实数a的绝对值,记为|a|,它是一个非负实数.
|a| =
a( a﹥0 )
0 ( a = 0)
-a( a﹤0)
几何意义: |a|表示点x到原点0的距离.而| a-b |表示点a与点b的距离.
倒数:
乘积是1的两个数互为倒数.若a与b互为倒数,则ab=1.
如果 a ≠ 0 ,那么它的倒数为 .
(1)分别写出- , 的相反数;
(3)求
(4)已知一个数的绝对值是
求这个数.
练习、填空:
(1) 的相反数是__________
(5) 绝对值是 _________
(2) 的倒数是__
(3)| | =___________
(4)绝对值等于 的数是 _________
的平方 是___
(6) 比较大小:-7
当数从有理数扩充到实数以后,实数之间不仅可以进行加 减 乘 除 乘方运算,又增加了非负数的开平方运算,任意实数可以进行开立方运算。进行实数运算时,有理数的运算法则及性质等同样适用。
【规律方法】实数运算的“三个关键”:
1. 运算法则:乘方和开方运算、幂的运算、指数(特别是负整数指数,0指数)运算、根式运算、特殊三角函数值的计算以及绝对值的化简等.
2. 运算顺序:先乘方,再乘除,后加减,有括号的先算括号里面的,在同一级运算中要从左到右依次运算,无论何种运算,都要注意先定符号后运算.
3. 运算律的使用:使用运算律可以简化运算,提高运算速度和准确度.
例2 计算下列各式的值
练习:
1.
2.
3.
4.
例3计算(结果保留小数点后两位)
巩固练习(一)
1.下列各数不是有理数的是( )
A.3.14 B.-π C.
D.
2.在
中是无理数的有( )
A. 2 个 B.3个 C.4个 D.1个
B
A
巩固练习(二)
(2)若
(3)
巩固练习(三)
再见!
