3.1匀速圆周运动快慢的描述同步练习 (word版含答案)
文档属性
| 名称 | 3.1匀速圆周运动快慢的描述同步练习 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-06 00:05:01 | ||
图片预览




文档简介
鲁科版 (2019)必修第二册 3.1 匀速圆周运动快慢的描述 同步练习
一、单选题
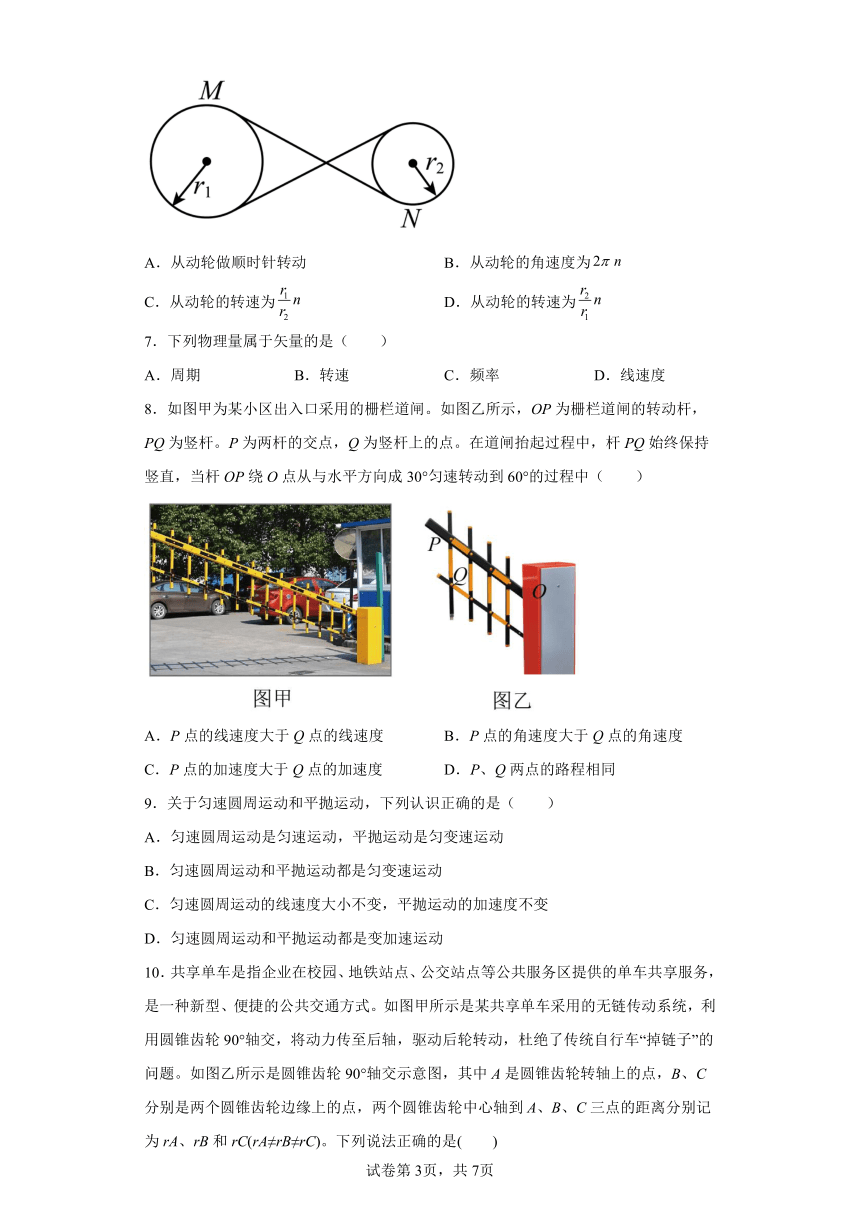
1.如图所示是建筑工地上起吊重物的吊车,某次操作过程中,液压杆收缩,吊臂绕固定转轴O顺时针转动,吊臂边缘的M、N两点做圆周运动,O、M、N三点不共线,此时M点的角速度为ω。已知MN=2OM=2L,则下列说法正确的是( )
A.M点的速度方向平行于N点的速度方向
B.N点的角速度
C.N点的向心加速度大小
D.M、N两点的线速度大小关系为
2.如图所示,如果把钟表上的时针、分针、秒针的运动看成匀速转动,那么,从它的分针与时针第一次重合至第二次重合,中间经历的时间为( )
A. B. C. D.
3.如图,A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面不打滑。下列说法正确的是( )
A.A与B线速度大小相等
B.B与C线速度大小相等
C.A与B角速度大小相等
D.B与C角速度大小相等
4.A、B两艘快艇在湖面上做匀速圆周运动,在相同时间内,它们通过的路程之比是4∶3,运动方向改变的角度之比是3∶2,则它们( )
A.线速度大小之比为2∶3
B.角速度大小之比为3∶4
C.圆周运动的半径之比为2∶1
D.转速之比为3∶2
5.如图所示,用起瓶器打开瓶盖,起瓶器上A、B两点绕O点转动的角速度分别为ωA和ωB,线速度大小分别为vA和vB,则( )
A.ωA=ωB,vA>vB B.ωA=ωB,vAC.ωA<ωB,vA=vB D.ωA>ωB,vA=vB
6.如图所示为某一皮带传动装置,主动轮的半径为,从动轮的半径为,已知主动轮做顺时针转动,转速为,转动过程中皮带不打滑,下列说法正确的是( )
A.从动轮做顺时针转动 B.从动轮的角速度为
C.从动轮的转速为 D.从动轮的转速为
7.下列物理量属于矢量的是( )
A.周期 B.转速 C.频率 D.线速度
8.如图甲为某小区出入口采用的栅栏道闸。如图乙所示,OP为栅栏道闸的转动杆,PQ为竖杆。P为两杆的交点,Q为竖杆上的点。在道闸抬起过程中,杆PQ始终保持竖直,当杆OP绕O点从与水平方向成30°匀速转动到60°的过程中( )
A.P点的线速度大于Q点的线速度 B.P点的角速度大于Q点的角速度
C.P点的加速度大于Q点的加速度 D.P、Q两点的路程相同
9.关于匀速圆周运动和平抛运动,下列认识正确的是( )
A.匀速圆周运动是匀速运动,平抛运动是匀变速运动
B.匀速圆周运动和平抛运动都是匀变速运动
C.匀速圆周运动的线速度大小不变,平抛运动的加速度不变
D.匀速圆周运动和平抛运动都是变加速运动
10.共享单车是指企业在校园、地铁站点、公交站点等公共服务区提供的单车共享服务,是一种新型、便捷的公共交通方式。如图甲所示是某共享单车采用的无链传动系统,利用圆锥齿轮90°轴交,将动力传至后轴,驱动后轮转动,杜绝了传统自行车“掉链子”的问题。如图乙所示是圆锥齿轮90°轴交示意图,其中A是圆锥齿轮转轴上的点,B、C分别是两个圆锥齿轮边缘上的点,两个圆锥齿轮中心轴到A、B、C三点的距离分别记为rA、rB和rC(rA≠rB≠rC)。下列说法正确的是( )
A.B点与C点的角速度:ωB=ωC
B.C点与A点的线速度:vC= vA
C.B点与A点的线速度:vB= vA
D.B点和C点的线速度:vB>vC
11.如图所示的皮带传动装置,皮带与圆盘O、O'之间不打滑。将三个相同的小物块分别放在圆盘O、O'边缘的A、B两点和圆盘O上的C点,三个小物块随圆盘做匀速圆周运动。A、B、C三物块做圆周运动的半径rA=2rB,rC=rB。小物块A、B运动的线速度之比和小物块B、C运动的周期之比分别为( )
A.2:1;1:1 B.2:1;1:2 C.1:1;2:1 D.1:1;1:2
12.骑自行车出行,不仅低碳环保,还能强身健体。自行车的大齿轮、小齿轮是相互关联的转动部分,其边缘有两个点A、B,如图所示。当大齿轮带动小齿轮匀速转动时,下列说法正确的是( )
A.A、B两点的线速度大小相等 B.A点的线速度比B点的线速度大
C.A点的线速度比B点的线速度小 D.A、B两点的周期相等
13.闹钟是带有闹时装置的钟。既能指示时间,又能按人们预定的时刻发出音响信号或其他信号。如图所示,机械式闹钟中的三个齿轮的半径之比为1:3:5,当齿轮转动的时候,小齿轮边缘的M点和大齿轮边缘的N点的线速度大小之比和角速度之比分别为( )
A.1:1 1:5 B.1:1 5:1 C.5:1 1:5 D.5:1 5:1
14.学校运动会增加了自创集体项目“同心追梦”。各班派出30名参赛选手,分成6组在两侧接力区进行接力比赛。比赛时5人一组共同抬着竹竿协作配合,以最快速度向标志物跑,到标志物前,以标志物为圆心,转一圈,继续向下一个标志物绕圈,分别绕完3个标志物后,进入到对面接力区域,将竹竿交给下一组参赛选手,直到全队完成比赛。假设五位质量不同的参赛选手与地面和竹竿的动摩擦因数相同,某次绕圈过程中角速度先增加后不变,竹竿长度为L,标志物和竹竿始终在一条直线上,最外围的同学做圆周运动的半径不变。下列说法正确的是( )
A.最外围同学的动能最大
B.最里面的同学最容易被甩出去
C.靠近外围的四位同学的线速度与他们到最里面同学的距离成正比
D.做匀速圆周运动过程中,最外围同学所受合外力始终水平指向圆心
15.结合生活常识可以判断钟表里时针转动的角速度和地球自转的角速度之比为( )
A.1:1 B.1:2 C.2:1 D.365:1
二、填空题
16.周期
(1)周期T:做匀速圆周运动的物体,运动一周所用的时间,单位:______;
(2)转速n:物体转动的______与所用时间之比.单位:______或______;
(3)周期和转速的关系: (n的单位为r/s时)。
17.判断题
(1)做匀速圆周运动的物体,相同时间内位移相同。( )
(2)做匀速圆周运动的物体,其线速度大小不变。( )
(3)匀速圆周运动是一种匀速运动。( )
(4)做匀速圆周运动的物体,其所受合力一定不为零。( )
(5)做匀速圆周运动的物体,其角速度不变。( )
(6)做匀速圆周运动的物体,周期越大,角速度越小。( )
18.如图所示,某种变速自行车,有六个飞轮和三个链轮,链轮和飞轮的齿数如下表所示,后轮的直径为d=666mm。当人骑该车,使脚踏板以恒定的角速度转动时,自行车行进的最大速度和最小速度之比为______;当人骑该车行进的速度为v=4m/s时,脚踩踏板作匀速圆周运动的最小角速度是______rad/s。
名 称 链 轮 飞 轮
齿数N/个 48 38 28 12 15 18 21 24 28
三、解答题
19.如图所示,一位同学玩飞镖游戏,圆盘最上端有一点P,飞镖抛出时与P在同一竖直面内等高,且距离P点为L。当飞镖以初速度v0垂直盘面瞄准P点抛出的同时,圆盘绕经过盘心O点的水平轴在竖直平面内匀速转动。忽略空气阻力,重力加速度为g,若飞镖恰好击中P点,求:
(1)圆盘的半径;
(2)圆盘转动角速度的值。
20.某同学以自行车的齿轮传动作为探究学习的课题,该同学通过观察发现,自行车的大齿轮与小齿轮通过链条相连,后轮与小齿轮绕共同的轴转动,如图所示,测得大齿轮的半径为r1、小齿轮的半径为r2、自行车后轮的半径为R,若测得在时间t内大齿轮转动的圈数为N,求:
(1)大齿轮转动角速度的大小ω;
(2)自行车后轮线速度的大小v。
21.如图所示,半径为R的水平圆盘绕垂直于盘面的中心轴匀速转动。若在圆心O正上方h处沿与半径OA平行的方向水平抛出一个小球,要使小球在圆盘上的落点为A,求:
(1)小球做平抛运动的初速度;
(2)圆盘转动的角速度。
22.皮带传动是常见的传动方式之一,可以建构如图所示的物理模型来分析其传动原理,该模型中A、B两轮同轴转动,A、B、C三轮半径大小的关系是==2若皮带不打滑,求:
(1)三个轮角速度的大小之比;
(2)三个轮边缘线速度的大小之比。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】
A.液压杆收缩,吊臂绕固定转轴O顺时针转动同时进行,M、N两点速度是收缩速度与转动速度的合速度,因为M、N两点转动线速度大小不同,则合速度的方向不同,即M点的速度方向不平行于N点的速度方向,故A错误。
B.M、N两点属于同轴转动,角速度相同,故N点的角速度也为ω,故B错误;
C.根据向心加速度的公式
及N点的角速度也ω,且
则
得
故C正确;
D.M、N两点的角速度相同,根据
得
D错误;
故选C。
2.A
【详解】
分针的角速度
时针的角速度
从它的分针与时针第一次重合至第二次重合,中间经历的时间为
故选A。
3.A
【详解】
A.据题意,这是摩擦传递装置,两轮边缘接触部分线速度大小相等,即,故选项A正确;
C.由于两轮半径不相同,据可知A、B两点角速度不相等,故选项C错误;
BD.由于A、C两点在同一轮上,角速度相等,,据可知
,
故BD错误;
故选A。
【点睛】
摩擦传递装置,接触边远部分线速度相等,可以判断A、B两点线速度相等;A、C两点在同一转动轮上,属于同轴转动体,同轴转动体除了转动轴,其他任意两点角速度相等,可以判断A、C两点角速度大小,进而比较B、C两点的线速度大小。
4.D
【详解】
A.根据线速度定义式v=,已知在相同时间内它们通过的路程之比是4∶3,则线速度大小之比为4∶3,故A错误;
B.根据角速度定义式ω=,相同时间内它们转过的角度之比为3∶2,则角速度之比为3∶2,故B错误;
C.根据公式v=rω,可得圆周运动半径r=,线速度大小之比为4∶3,角速度之比为3∶2,则圆周运动的半径之比为8∶9,故C错误;
D.根据T=得,周期之比为2∶3,再根据n=得转速之比为3∶2,故D正确。
故选D。
5.B
【详解】
同轴转动,角速度相等,故
由于,根据
故选B。
6.C
【详解】
A.主动轮做顺时针转动,由皮带缠绕的方式可知从动轮做逆时针转动,A错误;
B.两轮通过皮带传动,边缘的线速度大小相等,由
v=rω
ω=2πn
可得
则从动轮的角速度为
故B错误;
CD.同理可得
2πn·r1=2πn2·r2
解得从动轮的转速为
n2=
C正确,D错误;
故选C。
7.D
【详解】
A.周期是只有大小,没有方向的标量,A错误;
B.转速是只有大小,没有方向的标量,B错误;
C.频率是只有大小,没有方向的标量,C错误;
D.线速度是有大小,又有方向的矢量,D正确。
故选D。
8.D
【详解】
由于P、Q两点在同一杆上,而且杆运动时始终保持竖直,所以在30°匀速转动到60°的过程中,两点都做半径相同的匀速圆周运动,故两点的线速度、角速度、加速度和路程都相等。
故选D。
9.C
【详解】
ABD.做匀速圆周运动的物体速度大小是变化的,加速度大小不变,方向改变,所以是变速运动,平抛运动加速度恒定,所以是匀变速运动,故ABD错误;
C.匀速圆周运动的线速度大小不变,方向变化,平抛运动的加速度是重力加速度,不变,故C正确。
故C正确。
10.B
【详解】
AD.由图可知,B与C点属于齿轮传动,两点的速度是相等的,所以B点与C点的线速度相等,由于
rB≠rC
根据
v=rω
ωB≠ωC
故AD错误;
C.由图可知,A与B点属于同轴传动,具有相等的角速度,即
ωB=ωA
由
v=ωr
可得
即
vB=vA
故C错误;
B.B点与C点的线速度相等,所以
vC=vB=vA
故B正确。
故选B。
11.D
【详解】
AB是同缘转动,则线速度相等,即小物块A、B运动的线速度之比1:1;由于AB的线速度大小相等,由
ω═
所以ω于r成反比,又由于
则角速度与周期成反比,则周期与半径成正比。因此小物块B、A运动的周期之比为1:2,又A、C同轴,所以A、C两点的角速度之比为1:1,则它们的周期也相等。那么B、C运动的周期之比1:2;故D正确,ABC错误;
故选D。
【点睛】
两轮通过皮带传动,皮带与轮之间不打滑,说明它们边缘的线速度相等;再由角速度、向心加速度的公式逐个分析即可。
12.A
【详解】
ABC.边缘有两个点A、B是皮带传动,线速度大小相等,选项A正确,BC错误;
D.A、B两点线速度大小相等,而半径不相等,根据可知A、B两点的周期不相等,选项D错误。
故选A。
13.B
【详解】
根据题意可知,M点和N点属于同缘传动,边缘点的线速度相等,则线速度之比为,根据
可知
则
故ACD错误B正确。
故选B。
14.D
【详解】
A.五位同学都是绕障碍物做圆周运动,由v=ωr且ω相等可知最外围同学v最大,但m不相等,其动能不一定最大,故A错误;
B.最里面的同学运动半径最小,由可知,F向与m、r有关,r最小,但m未知,最里面的同学不一定最容易被甩出去,故B错误;
C.设最里面同学到转轴距离为r1,外围同学到最里面同学的间距为r2,则
则靠近外围的四位同学的线速度与他们到最里面同学的距离不成正比,故C错误;
D.做匀速圆周运动的物体由合外力提供向心力,即合外力指向圆心,故D正确。
故选D。
15.C
【详解】
时针转动的角速度
地球自转的角速度
则
故C正确。
故选C。
16. 秒 圈数 转每秒 转每分
【详解】
(1)[1]T:做匀速圆周运动的物体,运动一周所用的时间,单位:秒;
(2)[2][3][4]转速n:物体转动的圈数与所用时间之比.单位:转每秒或转每分。
17. 错误 正确 错误 正确 正确 正确
【详解】
(1)[1]做匀速圆周运动的物体,相同时间内位移大小相同,方向不同,故错误。
(2)[2]做匀速圆周运动的物体,其线速度大小不变,故正确。
(3)[3]匀速圆周运动的运动方向发生变化,不是匀速运动,故错误。
(4)[4]做匀速圆周运动的物体,其所受合力充当向心力,一定不为零。故正确。
(5)[5]做匀速圆周运动的物体,其角速度不变,故正确。
(6)[6]由角速度的定义式
可知做匀速圆周运动的物体,周期越大,角速度越小,故正确。
18. 4 3.0
【详解】
[1]链轮和飞轮的轮半径与齿数成正比,因为是依靠同一个链条传动,所以链轮与飞轮的轮缘线速度是一样的,所以
亦即
当N链=48,N飞=12时自行车速度最大,此时
ω飞=4ω链
当N链=28,N飞=28时,自行车速度最小,此时
ω飞=ω链
而自行车的速度
所以自行车的最大速度和最小速度之比为4。
[2]当自行车行驶速度一定时,即后轮的角速度一定,飞轮的角速度一定,根据
由于脚踏板和链轮有相同的角速度,使脚踩踏板作匀速圆周运动的角速度最小,则最多,最少,即N链=48,N飞=12,再由
可得
19.(1);(2)(k=0,1,2,…)
【详解】
(1)飞镖水平抛出后做平抛运动,在水平方向做匀速直线运动,因此飞行时间
飞镖击中P点时,P恰好在最下端,则
解得圆盘的半径为
(2)飞镖击中P点,则P点转过的角度θ满足θ=π+2kπ(k=0,1,2,…)
故
(k=0,1,2,…)
20.(1);(2)
【详解】
(1)大齿轮的周期
则
大齿轮转动角速度的大小
(2)大齿轮和小齿轮边缘线速度的大小相等,有
解得小齿轮角速度的大小
小齿轮角速度与后轮角速度的大小相等,则后轮线速度的大小
21.(1) ;(2)
【详解】
(1) 要使小球直接落在B点,水平位移要为R,对平抛的小球:水平方向:
,
联立得:
(2) 要使小球落到A处,则小球在下落的这段时间内,A点刚好转了n圈则:
ωt=2nπ (n=0、1、2…)
联立得:
22.(1);(2)
【详解】
(1)因为B、C两轮由不打滑的皮带相连,所以相等时间内B、C两点转过的弧长相等,即
由
知
又A、B是同轴转动,相等时间转过的角度相等,即
所以
(2)由
知
所以
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图所示是建筑工地上起吊重物的吊车,某次操作过程中,液压杆收缩,吊臂绕固定转轴O顺时针转动,吊臂边缘的M、N两点做圆周运动,O、M、N三点不共线,此时M点的角速度为ω。已知MN=2OM=2L,则下列说法正确的是( )
A.M点的速度方向平行于N点的速度方向
B.N点的角速度
C.N点的向心加速度大小
D.M、N两点的线速度大小关系为
2.如图所示,如果把钟表上的时针、分针、秒针的运动看成匀速转动,那么,从它的分针与时针第一次重合至第二次重合,中间经历的时间为( )
A. B. C. D.
3.如图,A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动,接触面不打滑。下列说法正确的是( )
A.A与B线速度大小相等
B.B与C线速度大小相等
C.A与B角速度大小相等
D.B与C角速度大小相等
4.A、B两艘快艇在湖面上做匀速圆周运动,在相同时间内,它们通过的路程之比是4∶3,运动方向改变的角度之比是3∶2,则它们( )
A.线速度大小之比为2∶3
B.角速度大小之比为3∶4
C.圆周运动的半径之比为2∶1
D.转速之比为3∶2
5.如图所示,用起瓶器打开瓶盖,起瓶器上A、B两点绕O点转动的角速度分别为ωA和ωB,线速度大小分别为vA和vB,则( )
A.ωA=ωB,vA>vB B.ωA=ωB,vA
6.如图所示为某一皮带传动装置,主动轮的半径为,从动轮的半径为,已知主动轮做顺时针转动,转速为,转动过程中皮带不打滑,下列说法正确的是( )
A.从动轮做顺时针转动 B.从动轮的角速度为
C.从动轮的转速为 D.从动轮的转速为
7.下列物理量属于矢量的是( )
A.周期 B.转速 C.频率 D.线速度
8.如图甲为某小区出入口采用的栅栏道闸。如图乙所示,OP为栅栏道闸的转动杆,PQ为竖杆。P为两杆的交点,Q为竖杆上的点。在道闸抬起过程中,杆PQ始终保持竖直,当杆OP绕O点从与水平方向成30°匀速转动到60°的过程中( )
A.P点的线速度大于Q点的线速度 B.P点的角速度大于Q点的角速度
C.P点的加速度大于Q点的加速度 D.P、Q两点的路程相同
9.关于匀速圆周运动和平抛运动,下列认识正确的是( )
A.匀速圆周运动是匀速运动,平抛运动是匀变速运动
B.匀速圆周运动和平抛运动都是匀变速运动
C.匀速圆周运动的线速度大小不变,平抛运动的加速度不变
D.匀速圆周运动和平抛运动都是变加速运动
10.共享单车是指企业在校园、地铁站点、公交站点等公共服务区提供的单车共享服务,是一种新型、便捷的公共交通方式。如图甲所示是某共享单车采用的无链传动系统,利用圆锥齿轮90°轴交,将动力传至后轴,驱动后轮转动,杜绝了传统自行车“掉链子”的问题。如图乙所示是圆锥齿轮90°轴交示意图,其中A是圆锥齿轮转轴上的点,B、C分别是两个圆锥齿轮边缘上的点,两个圆锥齿轮中心轴到A、B、C三点的距离分别记为rA、rB和rC(rA≠rB≠rC)。下列说法正确的是( )
A.B点与C点的角速度:ωB=ωC
B.C点与A点的线速度:vC= vA
C.B点与A点的线速度:vB= vA
D.B点和C点的线速度:vB>vC
11.如图所示的皮带传动装置,皮带与圆盘O、O'之间不打滑。将三个相同的小物块分别放在圆盘O、O'边缘的A、B两点和圆盘O上的C点,三个小物块随圆盘做匀速圆周运动。A、B、C三物块做圆周运动的半径rA=2rB,rC=rB。小物块A、B运动的线速度之比和小物块B、C运动的周期之比分别为( )
A.2:1;1:1 B.2:1;1:2 C.1:1;2:1 D.1:1;1:2
12.骑自行车出行,不仅低碳环保,还能强身健体。自行车的大齿轮、小齿轮是相互关联的转动部分,其边缘有两个点A、B,如图所示。当大齿轮带动小齿轮匀速转动时,下列说法正确的是( )
A.A、B两点的线速度大小相等 B.A点的线速度比B点的线速度大
C.A点的线速度比B点的线速度小 D.A、B两点的周期相等
13.闹钟是带有闹时装置的钟。既能指示时间,又能按人们预定的时刻发出音响信号或其他信号。如图所示,机械式闹钟中的三个齿轮的半径之比为1:3:5,当齿轮转动的时候,小齿轮边缘的M点和大齿轮边缘的N点的线速度大小之比和角速度之比分别为( )
A.1:1 1:5 B.1:1 5:1 C.5:1 1:5 D.5:1 5:1
14.学校运动会增加了自创集体项目“同心追梦”。各班派出30名参赛选手,分成6组在两侧接力区进行接力比赛。比赛时5人一组共同抬着竹竿协作配合,以最快速度向标志物跑,到标志物前,以标志物为圆心,转一圈,继续向下一个标志物绕圈,分别绕完3个标志物后,进入到对面接力区域,将竹竿交给下一组参赛选手,直到全队完成比赛。假设五位质量不同的参赛选手与地面和竹竿的动摩擦因数相同,某次绕圈过程中角速度先增加后不变,竹竿长度为L,标志物和竹竿始终在一条直线上,最外围的同学做圆周运动的半径不变。下列说法正确的是( )
A.最外围同学的动能最大
B.最里面的同学最容易被甩出去
C.靠近外围的四位同学的线速度与他们到最里面同学的距离成正比
D.做匀速圆周运动过程中,最外围同学所受合外力始终水平指向圆心
15.结合生活常识可以判断钟表里时针转动的角速度和地球自转的角速度之比为( )
A.1:1 B.1:2 C.2:1 D.365:1
二、填空题
16.周期
(1)周期T:做匀速圆周运动的物体,运动一周所用的时间,单位:______;
(2)转速n:物体转动的______与所用时间之比.单位:______或______;
(3)周期和转速的关系: (n的单位为r/s时)。
17.判断题
(1)做匀速圆周运动的物体,相同时间内位移相同。( )
(2)做匀速圆周运动的物体,其线速度大小不变。( )
(3)匀速圆周运动是一种匀速运动。( )
(4)做匀速圆周运动的物体,其所受合力一定不为零。( )
(5)做匀速圆周运动的物体,其角速度不变。( )
(6)做匀速圆周运动的物体,周期越大,角速度越小。( )
18.如图所示,某种变速自行车,有六个飞轮和三个链轮,链轮和飞轮的齿数如下表所示,后轮的直径为d=666mm。当人骑该车,使脚踏板以恒定的角速度转动时,自行车行进的最大速度和最小速度之比为______;当人骑该车行进的速度为v=4m/s时,脚踩踏板作匀速圆周运动的最小角速度是______rad/s。
名 称 链 轮 飞 轮
齿数N/个 48 38 28 12 15 18 21 24 28
三、解答题
19.如图所示,一位同学玩飞镖游戏,圆盘最上端有一点P,飞镖抛出时与P在同一竖直面内等高,且距离P点为L。当飞镖以初速度v0垂直盘面瞄准P点抛出的同时,圆盘绕经过盘心O点的水平轴在竖直平面内匀速转动。忽略空气阻力,重力加速度为g,若飞镖恰好击中P点,求:
(1)圆盘的半径;
(2)圆盘转动角速度的值。
20.某同学以自行车的齿轮传动作为探究学习的课题,该同学通过观察发现,自行车的大齿轮与小齿轮通过链条相连,后轮与小齿轮绕共同的轴转动,如图所示,测得大齿轮的半径为r1、小齿轮的半径为r2、自行车后轮的半径为R,若测得在时间t内大齿轮转动的圈数为N,求:
(1)大齿轮转动角速度的大小ω;
(2)自行车后轮线速度的大小v。
21.如图所示,半径为R的水平圆盘绕垂直于盘面的中心轴匀速转动。若在圆心O正上方h处沿与半径OA平行的方向水平抛出一个小球,要使小球在圆盘上的落点为A,求:
(1)小球做平抛运动的初速度;
(2)圆盘转动的角速度。
22.皮带传动是常见的传动方式之一,可以建构如图所示的物理模型来分析其传动原理,该模型中A、B两轮同轴转动,A、B、C三轮半径大小的关系是==2若皮带不打滑,求:
(1)三个轮角速度的大小之比;
(2)三个轮边缘线速度的大小之比。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】
A.液压杆收缩,吊臂绕固定转轴O顺时针转动同时进行,M、N两点速度是收缩速度与转动速度的合速度,因为M、N两点转动线速度大小不同,则合速度的方向不同,即M点的速度方向不平行于N点的速度方向,故A错误。
B.M、N两点属于同轴转动,角速度相同,故N点的角速度也为ω,故B错误;
C.根据向心加速度的公式
及N点的角速度也ω,且
则
得
故C正确;
D.M、N两点的角速度相同,根据
得
D错误;
故选C。
2.A
【详解】
分针的角速度
时针的角速度
从它的分针与时针第一次重合至第二次重合,中间经历的时间为
故选A。
3.A
【详解】
A.据题意,这是摩擦传递装置,两轮边缘接触部分线速度大小相等,即,故选项A正确;
C.由于两轮半径不相同,据可知A、B两点角速度不相等,故选项C错误;
BD.由于A、C两点在同一轮上,角速度相等,,据可知
,
故BD错误;
故选A。
【点睛】
摩擦传递装置,接触边远部分线速度相等,可以判断A、B两点线速度相等;A、C两点在同一转动轮上,属于同轴转动体,同轴转动体除了转动轴,其他任意两点角速度相等,可以判断A、C两点角速度大小,进而比较B、C两点的线速度大小。
4.D
【详解】
A.根据线速度定义式v=,已知在相同时间内它们通过的路程之比是4∶3,则线速度大小之比为4∶3,故A错误;
B.根据角速度定义式ω=,相同时间内它们转过的角度之比为3∶2,则角速度之比为3∶2,故B错误;
C.根据公式v=rω,可得圆周运动半径r=,线速度大小之比为4∶3,角速度之比为3∶2,则圆周运动的半径之比为8∶9,故C错误;
D.根据T=得,周期之比为2∶3,再根据n=得转速之比为3∶2,故D正确。
故选D。
5.B
【详解】
同轴转动,角速度相等,故
由于,根据
故选B。
6.C
【详解】
A.主动轮做顺时针转动,由皮带缠绕的方式可知从动轮做逆时针转动,A错误;
B.两轮通过皮带传动,边缘的线速度大小相等,由
v=rω
ω=2πn
可得
则从动轮的角速度为
故B错误;
CD.同理可得
2πn·r1=2πn2·r2
解得从动轮的转速为
n2=
C正确,D错误;
故选C。
7.D
【详解】
A.周期是只有大小,没有方向的标量,A错误;
B.转速是只有大小,没有方向的标量,B错误;
C.频率是只有大小,没有方向的标量,C错误;
D.线速度是有大小,又有方向的矢量,D正确。
故选D。
8.D
【详解】
由于P、Q两点在同一杆上,而且杆运动时始终保持竖直,所以在30°匀速转动到60°的过程中,两点都做半径相同的匀速圆周运动,故两点的线速度、角速度、加速度和路程都相等。
故选D。
9.C
【详解】
ABD.做匀速圆周运动的物体速度大小是变化的,加速度大小不变,方向改变,所以是变速运动,平抛运动加速度恒定,所以是匀变速运动,故ABD错误;
C.匀速圆周运动的线速度大小不变,方向变化,平抛运动的加速度是重力加速度,不变,故C正确。
故C正确。
10.B
【详解】
AD.由图可知,B与C点属于齿轮传动,两点的速度是相等的,所以B点与C点的线速度相等,由于
rB≠rC
根据
v=rω
ωB≠ωC
故AD错误;
C.由图可知,A与B点属于同轴传动,具有相等的角速度,即
ωB=ωA
由
v=ωr
可得
即
vB=vA
故C错误;
B.B点与C点的线速度相等,所以
vC=vB=vA
故B正确。
故选B。
11.D
【详解】
AB是同缘转动,则线速度相等,即小物块A、B运动的线速度之比1:1;由于AB的线速度大小相等,由
ω═
所以ω于r成反比,又由于
则角速度与周期成反比,则周期与半径成正比。因此小物块B、A运动的周期之比为1:2,又A、C同轴,所以A、C两点的角速度之比为1:1,则它们的周期也相等。那么B、C运动的周期之比1:2;故D正确,ABC错误;
故选D。
【点睛】
两轮通过皮带传动,皮带与轮之间不打滑,说明它们边缘的线速度相等;再由角速度、向心加速度的公式逐个分析即可。
12.A
【详解】
ABC.边缘有两个点A、B是皮带传动,线速度大小相等,选项A正确,BC错误;
D.A、B两点线速度大小相等,而半径不相等,根据可知A、B两点的周期不相等,选项D错误。
故选A。
13.B
【详解】
根据题意可知,M点和N点属于同缘传动,边缘点的线速度相等,则线速度之比为,根据
可知
则
故ACD错误B正确。
故选B。
14.D
【详解】
A.五位同学都是绕障碍物做圆周运动,由v=ωr且ω相等可知最外围同学v最大,但m不相等,其动能不一定最大,故A错误;
B.最里面的同学运动半径最小,由可知,F向与m、r有关,r最小,但m未知,最里面的同学不一定最容易被甩出去,故B错误;
C.设最里面同学到转轴距离为r1,外围同学到最里面同学的间距为r2,则
则靠近外围的四位同学的线速度与他们到最里面同学的距离不成正比,故C错误;
D.做匀速圆周运动的物体由合外力提供向心力,即合外力指向圆心,故D正确。
故选D。
15.C
【详解】
时针转动的角速度
地球自转的角速度
则
故C正确。
故选C。
16. 秒 圈数 转每秒 转每分
【详解】
(1)[1]T:做匀速圆周运动的物体,运动一周所用的时间,单位:秒;
(2)[2][3][4]转速n:物体转动的圈数与所用时间之比.单位:转每秒或转每分。
17. 错误 正确 错误 正确 正确 正确
【详解】
(1)[1]做匀速圆周运动的物体,相同时间内位移大小相同,方向不同,故错误。
(2)[2]做匀速圆周运动的物体,其线速度大小不变,故正确。
(3)[3]匀速圆周运动的运动方向发生变化,不是匀速运动,故错误。
(4)[4]做匀速圆周运动的物体,其所受合力充当向心力,一定不为零。故正确。
(5)[5]做匀速圆周运动的物体,其角速度不变,故正确。
(6)[6]由角速度的定义式
可知做匀速圆周运动的物体,周期越大,角速度越小,故正确。
18. 4 3.0
【详解】
[1]链轮和飞轮的轮半径与齿数成正比,因为是依靠同一个链条传动,所以链轮与飞轮的轮缘线速度是一样的,所以
亦即
当N链=48,N飞=12时自行车速度最大,此时
ω飞=4ω链
当N链=28,N飞=28时,自行车速度最小,此时
ω飞=ω链
而自行车的速度
所以自行车的最大速度和最小速度之比为4。
[2]当自行车行驶速度一定时,即后轮的角速度一定,飞轮的角速度一定,根据
由于脚踏板和链轮有相同的角速度,使脚踩踏板作匀速圆周运动的角速度最小,则最多,最少,即N链=48,N飞=12,再由
可得
19.(1);(2)(k=0,1,2,…)
【详解】
(1)飞镖水平抛出后做平抛运动,在水平方向做匀速直线运动,因此飞行时间
飞镖击中P点时,P恰好在最下端,则
解得圆盘的半径为
(2)飞镖击中P点,则P点转过的角度θ满足θ=π+2kπ(k=0,1,2,…)
故
(k=0,1,2,…)
20.(1);(2)
【详解】
(1)大齿轮的周期
则
大齿轮转动角速度的大小
(2)大齿轮和小齿轮边缘线速度的大小相等,有
解得小齿轮角速度的大小
小齿轮角速度与后轮角速度的大小相等,则后轮线速度的大小
21.(1) ;(2)
【详解】
(1) 要使小球直接落在B点,水平位移要为R,对平抛的小球:水平方向:
,
联立得:
(2) 要使小球落到A处,则小球在下落的这段时间内,A点刚好转了n圈则:
ωt=2nπ (n=0、1、2…)
联立得:
22.(1);(2)
【详解】
(1)因为B、C两轮由不打滑的皮带相连,所以相等时间内B、C两点转过的弧长相等,即
由
知
又A、B是同轴转动,相等时间转过的角度相等,即
所以
(2)由
知
所以
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
