九年级下册数学第三章圆单元测试四(附答案)
文档属性
| 名称 | 九年级下册数学第三章圆单元测试四(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 343.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-28 15:04:41 | ||
图片预览


文档简介
九年级下册数学第三章圆单元测试四(附答案)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,点A、B、C在⊙O上,∠ABC=30°,则∠OAC等于 ( )
A.60° B.45° C.35° D.30°
2.已知扇形的半径为2,圆心角为60°,则扇形的弧长为 ( )
A. B. C. D.
3.如图,⊙、⊙相内切于点A,其半径分别是2和1,将⊙沿直线平移至两圆再次相切时,则点移动的长度是( )
A.4 B.8 C.2 D.2 或4
4.已知两圆外切,圆心距为5cm,若其中一个圆的半径是3cm,则另一个圆的半径是( )
A. 8cm B.5cm C.3cm D.2cm
5.如图,⊙O是⊿ABC的外接圆,已知AD平分∠BAC交⊙O于点D,AD=5,BD=2,则DE的长为( )
A. B. C. D.
6.如图所示,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2.则BD的长为( )
A. B. C. D.
7.如图,⊙O的直径AB的长为10,弦AC长为6,∠ACB的平分线交⊙O于D,则AD长为( )
A. 8 B. 5 C. D.
8.如图,如果从半径为9cm的圆形纸片剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( )
A、6cm B、cm C、8cm D、cm
9.在半径为1的⊙O中,120°的圆心角所对的弧长是( )
A. B. C. D.
10.两圆的半径分别为3和7,圆心距为7,则两圆的位置关系是 ( )
A.内切 B.相交 C.外切 D.外离
二、填空题
11.已知一个圆的半径为5cm,则它的内接正六边形的边长为
12.如图,点P在双曲线y=上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是 ___________.
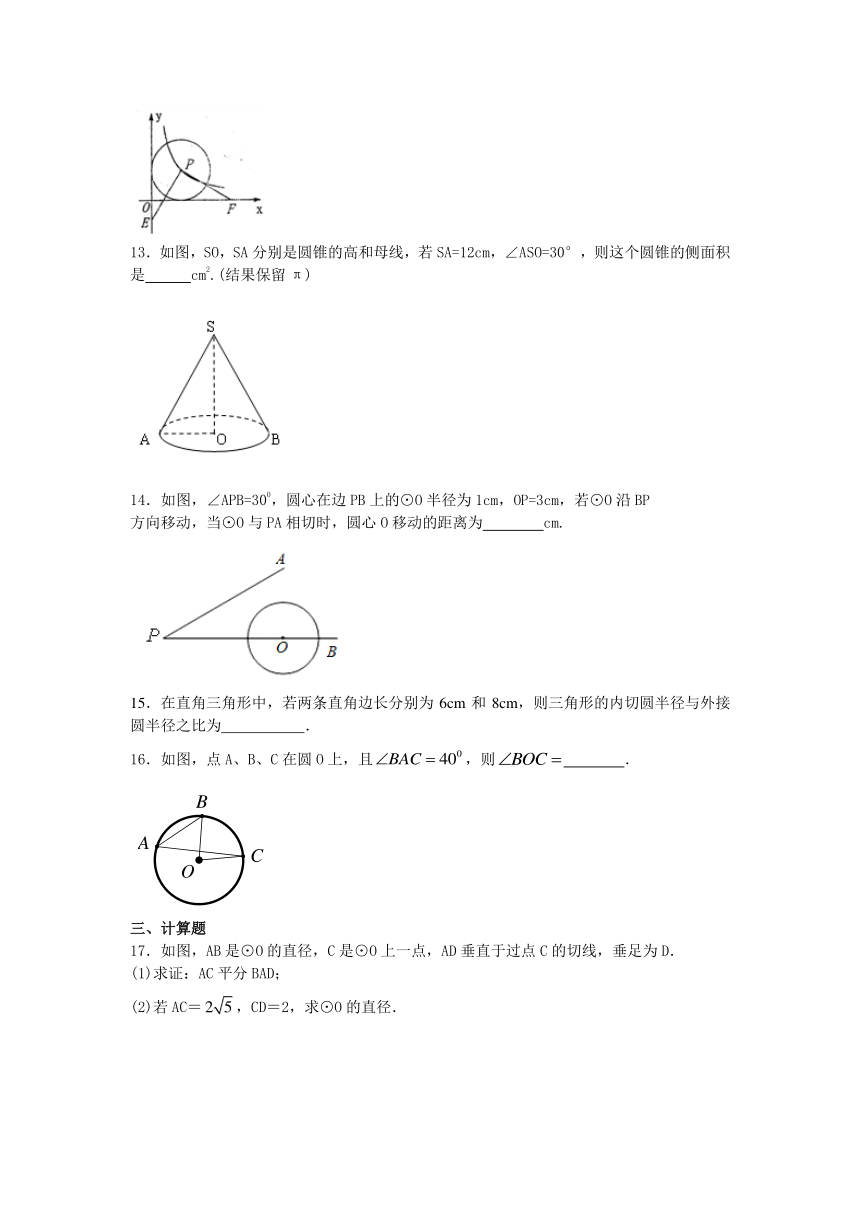
13.如图,SO,SA分别是圆锥的高和母线,若SA=12cm,∠ASO=30°,则这个圆锥的侧面积是 cm2.(结果保留π)
14.如图,∠APB=300,圆心在边PB上的⊙O半径为1cm,OP=3cm,若⊙O沿BP
方向移动,当⊙O与PA相切时,圆心O移动的距离为 cm.
15.在直角三角形中,若两条直角边长分别为6cm和8cm,则三角形的内切圆半径与外接圆半径之比为 .
16.如图,点A、B、C在圆O上,且,则 .
三、计算题
17.如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的切线,垂足为D.
(1)求证:AC平分BAD;
(2)若AC=,CD=2,求⊙O的直径.
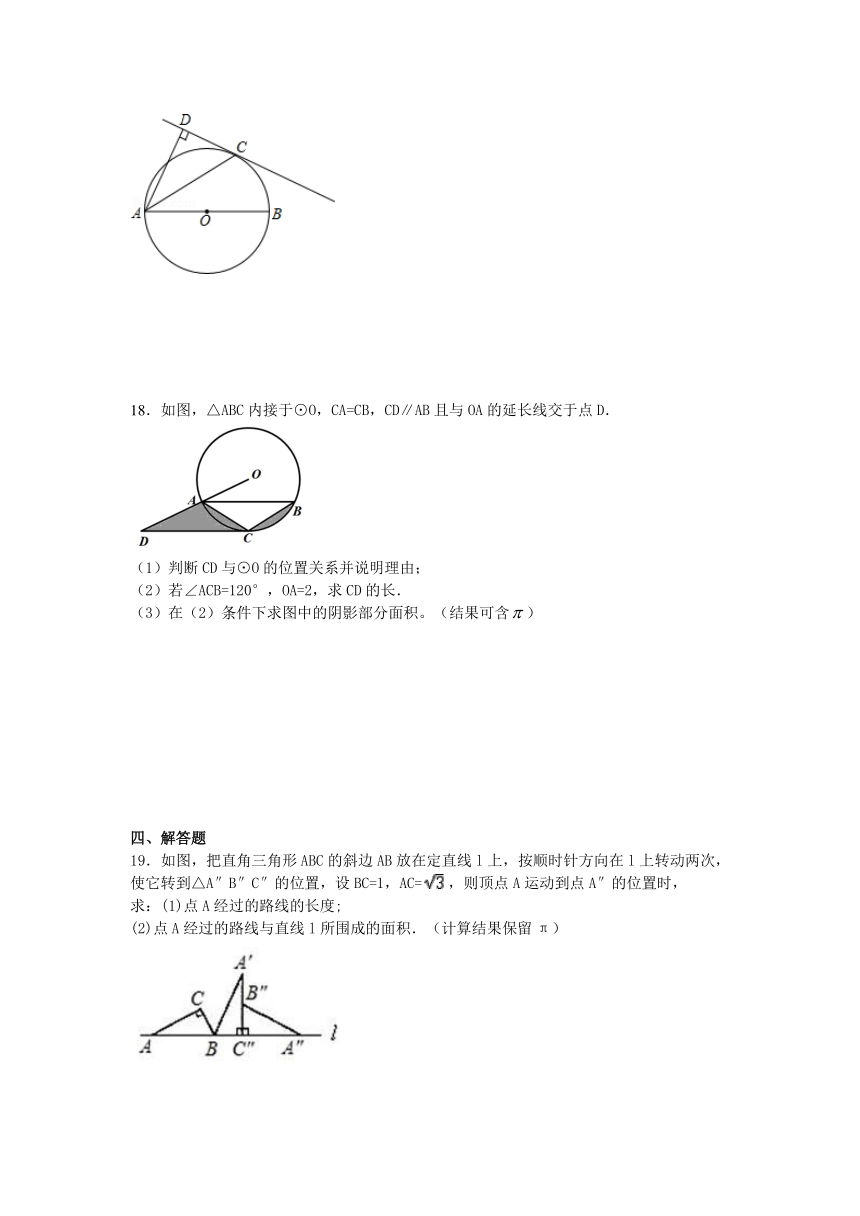
18.如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点D.
(1)判断CD与⊙O的位置关系并说明理由;
(2)若∠ACB=120°,OA=2,求CD的长.
(3)在(2)条件下求图中的阴影部分面积。(结果可含)
四、解答题
19.如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置,设BC=1,AC=,则顶点A运动到点A″的位置时,
求:(1)点A经过的路线的长度;
(2)点A经过的路线与直线l所围成的面积.(计算结果保留π)
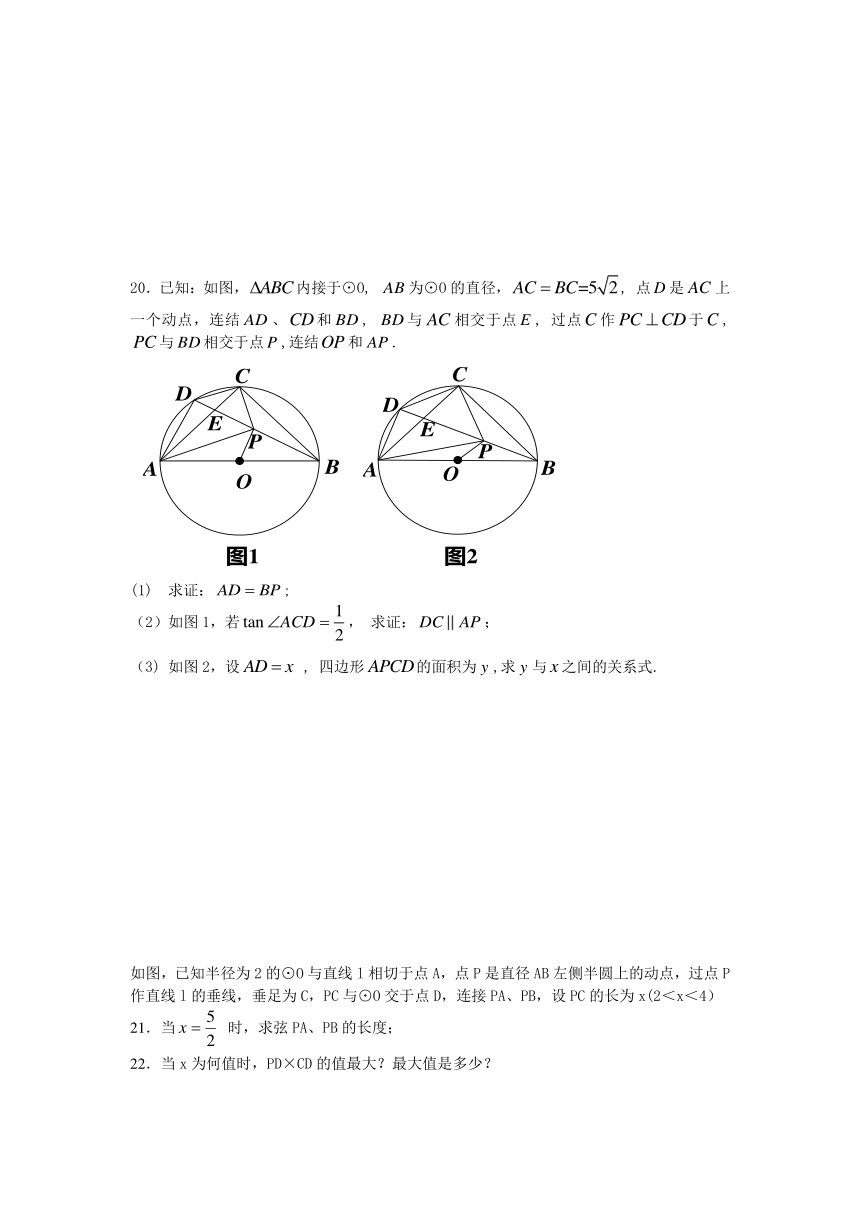
20.已知:如图,内接于⊙O, 为⊙O的直径,, 点是上一个动点,连结、和, 与相交于点, 过点作于, 与相交于点,连结和.
(1) 求证:;
(2)如图1,若, 求证:;
(3) 如图2,设 , 四边形的面积为,求与之间的关系式.
如图,已知半径为2的⊙O与直线l相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线l的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x<4)
21.当 时,求弦PA、PB的长度;
22.当x为何值时,PD×CD的值最大?最大值是多少?
23.如图,在中,,以AC为直径作,交AB于D,过O作OE//AB,交BC于E,求证:ED为的切线.
如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D.
24.若∠AOC=48°,求∠ACD的度数;
25.若AB=8,AD=2,求AC的长
26.写出阴影部分的面积
27.如图,圆O的直径为5,在圆O上位于直径AB的异侧有定点C和动点P,已知BC:CA=4: 3,点P在半圆弧AB上运动(不与A、B两点重合),过点C作CP的垂线CD交PB的延长线于D点.
(1)求证:AC·CD=PC·BC;
(2)当点P运动到AB弧中点时,求CD的长;
(3)当点P运动到什么位置时,△PCD的面积最大?并求出这个最大面积S。
参考答案
1.A
2.C
3.D
4.D
5.D
6.C
7.D
8.B
9.B
10.B
11.5cm。
12.4
13.。
14.1或5
15.2:5
16.
17.解:(1)如图:连接OC。
∵DC切⊙O于C,∴AD⊥CD。
∴∠ADC=∠OCF=90°。∴AD∥OC。
∴∠DAC=∠OCA。
∵OA=OC,∴∠OAC=∠OCA。
∴∠DAC=∠OAC,即AC平分∠BAD。
(2)连接BC。
在Rt△ADC中,AC=,CD=2,∴AD=4。
∵AB是直径,∴∠ACB=90°=∠ADC。
∵∠OAC=∠OCA,∴△ADC∽△ACB。
∴,即。
∴AB=5。
18.1)CD与⊙O相切,证明略; 3分
(2) ;2分
(3)。3分
19.(1)Rt△ABC中,BC=1,AC=,
则可得AB=2,∠CAB=30°,
则点A到A″所经过的路线为:
l弧AA′+l弧A′A″==.
(2)点A经过的路线与直线l围成的面积为:
+×1×+=.
20.(1) 证明: ∵, 为的直径
∴
∵,
∴
∵
∴是等腰直角三角形
∴
∴
∴是等腰直角三角形
∴
∴≌
∴
(2)证明:∵
∴
∴
∴
∴是的中点
∴
∴是等腰直角三角形
∴
∴
∴∥
(3)解:
= ()
21.PA=,PB=
22.当时, PD×CD 有最大值,最大值是2.
23.连OD,
∵OE//AB
∴∠EOC=∠A,∠EOD=∠ODA
又∵OA=OD
∴∠A=∠ODA
∴∠EOC=∠EOD
又OE=OE OC=OD
∴△EOC≌△EOD
∴∠EDO=∠ECO 又∠C=90°
∴∠EDO=90°
即ED⊥DO 而点D在上 ∴ED为的切线
24.∵OA=OC,∠AOC=48° ∴∠OAC=∠OCA=66°……1分
∵CD是⊙O的切线, ∴OC⊥CD……1分 ∴∠ACD=90°-∠OCA=24°……2分
25.连结BC ∵AB是⊙O的直径,∴∠BCA=90°……1分
又∵OC⊥CD ∴∠ADC=∠BCA=90°……1分
∴∠B+∠BAC=90°,∠ACD+∠OCA=90° ∴∠B=∠ACD……1分
∴△ABC∽△ACD……1分 ∴ ……1分
∴=16 ∴AC=4……1分
26.阴影部分面积==.
27.(1)略(2)(3)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,点A、B、C在⊙O上,∠ABC=30°,则∠OAC等于 ( )
A.60° B.45° C.35° D.30°
2.已知扇形的半径为2,圆心角为60°,则扇形的弧长为 ( )
A. B. C. D.
3.如图,⊙、⊙相内切于点A,其半径分别是2和1,将⊙沿直线平移至两圆再次相切时,则点移动的长度是( )
A.4 B.8 C.2 D.2 或4
4.已知两圆外切,圆心距为5cm,若其中一个圆的半径是3cm,则另一个圆的半径是( )
A. 8cm B.5cm C.3cm D.2cm
5.如图,⊙O是⊿ABC的外接圆,已知AD平分∠BAC交⊙O于点D,AD=5,BD=2,则DE的长为( )
A. B. C. D.
6.如图所示,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2.则BD的长为( )
A. B. C. D.
7.如图,⊙O的直径AB的长为10,弦AC长为6,∠ACB的平分线交⊙O于D,则AD长为( )
A. 8 B. 5 C. D.
8.如图,如果从半径为9cm的圆形纸片剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( )
A、6cm B、cm C、8cm D、cm
9.在半径为1的⊙O中,120°的圆心角所对的弧长是( )
A. B. C. D.
10.两圆的半径分别为3和7,圆心距为7,则两圆的位置关系是 ( )
A.内切 B.相交 C.外切 D.外离
二、填空题
11.已知一个圆的半径为5cm,则它的内接正六边形的边长为
12.如图,点P在双曲线y=上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF-OE的值是 ___________.
13.如图,SO,SA分别是圆锥的高和母线,若SA=12cm,∠ASO=30°,则这个圆锥的侧面积是 cm2.(结果保留π)
14.如图,∠APB=300,圆心在边PB上的⊙O半径为1cm,OP=3cm,若⊙O沿BP
方向移动,当⊙O与PA相切时,圆心O移动的距离为 cm.
15.在直角三角形中,若两条直角边长分别为6cm和8cm,则三角形的内切圆半径与外接圆半径之比为 .
16.如图,点A、B、C在圆O上,且,则 .
三、计算题
17.如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的切线,垂足为D.
(1)求证:AC平分BAD;
(2)若AC=,CD=2,求⊙O的直径.
18.如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点D.
(1)判断CD与⊙O的位置关系并说明理由;
(2)若∠ACB=120°,OA=2,求CD的长.
(3)在(2)条件下求图中的阴影部分面积。(结果可含)
四、解答题
19.如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置,设BC=1,AC=,则顶点A运动到点A″的位置时,
求:(1)点A经过的路线的长度;
(2)点A经过的路线与直线l所围成的面积.(计算结果保留π)
20.已知:如图,内接于⊙O, 为⊙O的直径,, 点是上一个动点,连结、和, 与相交于点, 过点作于, 与相交于点,连结和.
(1) 求证:;
(2)如图1,若, 求证:;
(3) 如图2,设 , 四边形的面积为,求与之间的关系式.
如图,已知半径为2的⊙O与直线l相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线l的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x<4)
21.当 时,求弦PA、PB的长度;
22.当x为何值时,PD×CD的值最大?最大值是多少?
23.如图,在中,,以AC为直径作,交AB于D,过O作OE//AB,交BC于E,求证:ED为的切线.
如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D.
24.若∠AOC=48°,求∠ACD的度数;
25.若AB=8,AD=2,求AC的长
26.写出阴影部分的面积
27.如图,圆O的直径为5,在圆O上位于直径AB的异侧有定点C和动点P,已知BC:CA=4: 3,点P在半圆弧AB上运动(不与A、B两点重合),过点C作CP的垂线CD交PB的延长线于D点.
(1)求证:AC·CD=PC·BC;
(2)当点P运动到AB弧中点时,求CD的长;
(3)当点P运动到什么位置时,△PCD的面积最大?并求出这个最大面积S。
参考答案
1.A
2.C
3.D
4.D
5.D
6.C
7.D
8.B
9.B
10.B
11.5cm。
12.4
13.。
14.1或5
15.2:5
16.
17.解:(1)如图:连接OC。
∵DC切⊙O于C,∴AD⊥CD。
∴∠ADC=∠OCF=90°。∴AD∥OC。
∴∠DAC=∠OCA。
∵OA=OC,∴∠OAC=∠OCA。
∴∠DAC=∠OAC,即AC平分∠BAD。
(2)连接BC。
在Rt△ADC中,AC=,CD=2,∴AD=4。
∵AB是直径,∴∠ACB=90°=∠ADC。
∵∠OAC=∠OCA,∴△ADC∽△ACB。
∴,即。
∴AB=5。
18.1)CD与⊙O相切,证明略; 3分
(2) ;2分
(3)。3分
19.(1)Rt△ABC中,BC=1,AC=,
则可得AB=2,∠CAB=30°,
则点A到A″所经过的路线为:
l弧AA′+l弧A′A″==.
(2)点A经过的路线与直线l围成的面积为:
+×1×+=.
20.(1) 证明: ∵, 为的直径
∴
∵,
∴
∵
∴是等腰直角三角形
∴
∴
∴是等腰直角三角形
∴
∴≌
∴
(2)证明:∵
∴
∴
∴
∴是的中点
∴
∴是等腰直角三角形
∴
∴
∴∥
(3)解:
= ()
21.PA=,PB=
22.当时, PD×CD 有最大值,最大值是2.
23.连OD,
∵OE//AB
∴∠EOC=∠A,∠EOD=∠ODA
又∵OA=OD
∴∠A=∠ODA
∴∠EOC=∠EOD
又OE=OE OC=OD
∴△EOC≌△EOD
∴∠EDO=∠ECO 又∠C=90°
∴∠EDO=90°
即ED⊥DO 而点D在上 ∴ED为的切线
24.∵OA=OC,∠AOC=48° ∴∠OAC=∠OCA=66°……1分
∵CD是⊙O的切线, ∴OC⊥CD……1分 ∴∠ACD=90°-∠OCA=24°……2分
25.连结BC ∵AB是⊙O的直径,∴∠BCA=90°……1分
又∵OC⊥CD ∴∠ADC=∠BCA=90°……1分
∴∠B+∠BAC=90°,∠ACD+∠OCA=90° ∴∠B=∠ACD……1分
∴△ABC∽△ACD……1分 ∴ ……1分
∴=16 ∴AC=4……1分
26.阴影部分面积==.
27.(1)略(2)(3)
