九年级下册数学第三章圆单元测试十三(附答案)
文档属性
| 名称 | 九年级下册数学第三章圆单元测试十三(附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 134.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-28 00:00:00 | ||
图片预览




文档简介
九年级下册数学第三章圆单元测试十三(附答案)
学校:___________姓名:___________班级:___________考号:___________
题号
一
二
三
四
总分
得分
第I卷(选择题)
评卷人
得分
一、选择题
1.如图,已知为的直径,切于点A, 则下列结论不一定正确的是( )
A. B. C. D.
2.在Rt△ABC中,∠ C=90°,BC=1,AC=2,则tanA的值为( )
A.2 B. C. D.
3.如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为( )
A、1 B、 C、2 D、2
4.如图,已知BD是⊙O直径,点A、C在⊙O上, =,∠AOB=60°,则∠BDC的度数是( )
A.20° B.25° C.30° D. 40°
5.已知两圆的半径分别是2 cm和4 cm,圆心距是2cm,那么这两个圆的位置关系是( )
A.外离 B.外切 C.相交 D.内切
6.已知⊙O1、⊙O2的半径分别是,若两圆相交,则圆心距O1O2可能取的值是( )
A.2 B.4 C.6 D.8
7.在半径为R的圆内有长为R的弦,则此弦所对的圆周角是 ( )
A.30° B.60° C.30°或150° D.60°或120°
8.如图,小正方形的边长均为1,扇形OAB是某圆锥的侧面展开图,则这个圆锥的底面周长为( )
A. B. C.2 D.3
9.已知⊙O1和⊙O2相切,两圆的圆心距为10cm,⊙O1的半径为4cm,则⊙O2的半径为( ).
(A)3cm (B)6或14cm (C)2cm (D)4cm
10.已知半径分别为3 cm和1cm的两圆相交,则它们的圆心距可能是( )
A.1 cm B.3 cm C.5cm D.7cm
第II卷(非选择题)
评卷人
得分
二、填空题
11.在⊙O中,弦AB= 16cm,弦心距OC= 6cm,那么该圆的半径为 cm.
12.已知两圆的半径分别为2和3,两圆的圆心距为4,那么这两圆的位置关系是 .
13.直角三角形的两边长分别为16和12,则此三角形的外接圆半径是 .
14. 在直角坐标系中,以P(3,1)为圆心,r为半径的圆与坐标轴恰好有三个公共点,则r的值为 。
15.若扇形的圆心角为60°,弧长为2,则扇形的半径为 .
16.若等边三角形ABC的边长为cm,以点A为圆心,以3cm为半径作⊙A,则BC所在直线与⊙A的位置关系是_________.
评卷人
得分
三、计算题
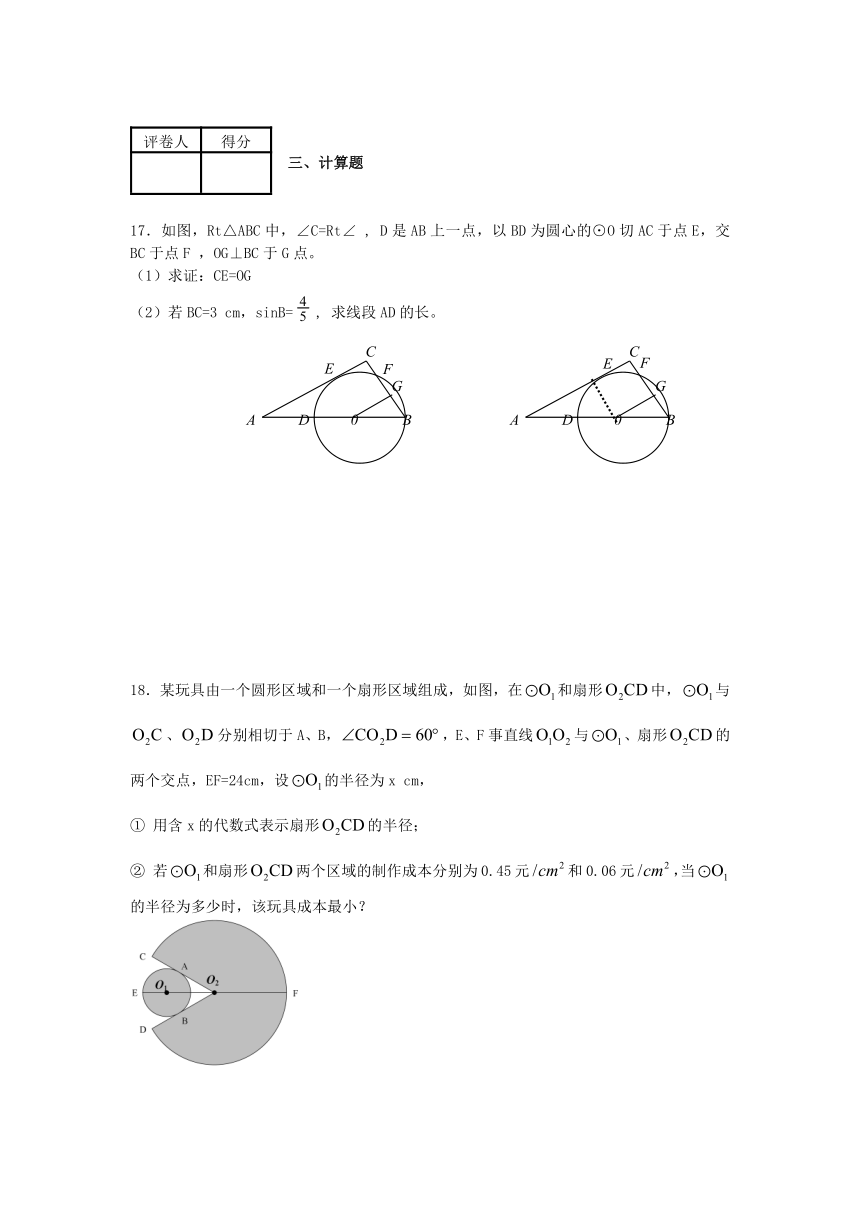
17.如图,Rt△ABC中,∠C=Rt∠ , D是AB上一点,以BD为圆心的⊙O切AC于点E,交BC于点F ,OG⊥BC于G点。
(1)求证:CE=OG
(2)若BC=3 cm,sinB=, 求线段AD的长。
18.某玩具由一个圆形区域和一个扇形区域组成,如图,在和扇形中,与、分别相切于A、B,,E、F事直线与、扇形的两个交点,EF=24cm,设的半径为x cm,
① 用含x的代数式表示扇形的半径;
② 若和扇形两个区域的制作成本分别为0.45元和0.06元,当的半径为多少时,该玩具成本最小?
评卷人
得分
四、解答题
19.如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60o.
(1)求⊙O的直径;
(2)若D是AB延长线上一点,连结CD,当BD长为多少时,CD与⊙O相切;
(3)若动点E以2cm/s的速度从A点出发沿着AB方向运动,同时动点F以1cm/s的速度从B点出发沿BC方向运动,设运动时间为,连结EF,当为何值时,△BEF为直角三角形.
如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D作DF⊥AB于点E,交O于点F,已知OE=1cm,DF=4cm.
20.求⊙O的半径
21.求切线CD的长
22.如图,已知⊙O的直径AB垂直于弦CD,垂足为E,F为CD延长线上一点,AF交⊙O于点G. 求证:AC2=AG·AF
已知:正方形ABCD的边长为2,⊙O交正方形ABCD的对角线AC所在直线于点T,连结TO交⊙O于点S,连结AS.
23.如图1,当⊙O经过A、D两点且圆心O在正方形ABCD内部时,连结DT、DS.
①试判断线段DT、DS的数量关系和位置关系; ②求AS+AT的值;
24.如图2,当⊙O经过A、D两点且圆心O在正方形ABCD外部时,连结DT、DS.求AS-AT的值;
25.如图3,延长DA到点E,使AE=AD,当⊙O经过A、E两点时,连结ET、ES.
根据(1)、(2)计算,通过观察、分析,对线段AS、AT的数量关系提出问题并解答.
26.推理证明:如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D过D作DE⊥BC,垂足为E,连结OE,CD=,∠ACB=30°.
(1)求证:DE是⊙O的切线;
(2)分别求AB,OE的长;
(3)填空:如果以点E为圆心,r为半径的圆上总存在不同的两点到点O的距离为1,则r的取值范围为 .
27.如图,PA 为⊙O的切线,B、D为⊙O上的两点,如果∠APB=,∠ADB=.(1)试判断直线PB与⊙O的位置关系,并说明理由;(2)如果D点是优弧AB上的一个动点,当且四边形ADBP是菱形时,求扇形OAMD的面积.
如图,矩形ABCD中,AB=6,BC=3.点E在线段BA上从B点以每秒1个单位的速度出发向A点运动,F是射线CD上一动点,在点E、F运动的过程中始终保持EF=5,且CF>BE,点P是EF的中点,连接AP.设点E运动时间为ts.
28.在点E运动过程中,AP的长度是如何变化的?( )
A.一直变短 B.一直变长 C.先变长后变短 D.先变短后变长
29.在点E、F运动的过程中,AP的长度存在一个最小值,当AP的长度取得最小值时,点P的位置应该在 .
30.以P为圆心作⊙P,当⊙P与矩形ABCD三边所在直线都相切时,求出此时t的值,并指出此时⊙P的半径长.
参考答案
1.D
2.B
3.D
4.C
5.D
6.B
7.C
8.B
9.B
10.B
11.10
12.相交。
13.8或10。
14.3或
15.6
16.相切
17.(1)证明:连接OE,
∵⊙O切AC于点E ∴∠OEC=900
∵∠ACB=∠CGO=Rt∠
∴四边形OGCE是矩形 ∴CE=OG
(2)解:在Rt△ABC中,sinB=
∴cosB=BC/AB=3/5
∵BC=3 ∴AB=BC÷cosB=3×5/3=5 cm
∵∠A=∠A , ∠AEO=∠ACB=Rt∠
∴△AEO∽△ACB
∴ 即
∴OB=
∴DO=2OB=
∴AD=AB-DB=5-=
18.解:(1)连接O1A。
∵⊙O1与O2C、O2D分别切一点A、B,
∴O1A⊥O2C,O2E平分∠CO2D。
∵,∴∠AO2O1=∠CO2D=30°。
在Rt△O1AO2中,,∴O1O2=A O1 sin∠AO2O1 =x sin30° =2x。
∵EF=24cm,∴FO2=EF-EO1-O1O2=24-3x,即扇形O2CD的半径为(24-3x)cm。
(2)设该玩具的制作成本为y元,则
。
∴当x=4时,y的值最小。
答:当⊙O1的半径为4cm时,该玩具的制作成本最小。
19.(1)4(2)
20.连接.
在中,直径弦于点,
cm.………………………………2分
在中,cm,cm,
(cm). ……………………………………4分
21.切于点,于点.
在与中,,,
. ……………………………………………………6分
,即.
(cm).
22.略
23.①线段DT、DS的数量和位置关系分别是DT=DS和DT⊥DS…2分
………3分
②证△DAS≌△DCT ……4分
∴AS+AT= …………5分
24.证△DAS≌△DCT …………6分
∴AS-AT= …………8分
25.提出的问题是:求 AT-AS 的值. …………10分
在TA上取TF=AS,连结EF,证△EAS≌△EFT …………11分
∴ AT-AS = …………12分
26.(1)见解析(2)2,(3)
27.⑴相切,理由:略⑵24π;
28.D
29.AD的中点
30.如图3,当⊙P在矩形ABCD内分别与AB、AD、CD相切于点Q、R、N时.
连接PQ、PR、PN,则PQ⊥AB、PR⊥AD、PN⊥CD
则四边形AQPR与四边形RPND为两个全等的正方形
∴PQ=AQ =AR=DR =AD=
在Rt△PQE中,EP=,由勾股定理可得:EQ=2
∴BE=BA-EQ-AQ=6-2-=
∴ t=,此时⊙P的半径为…
如图4,当⊙P在矩形ABCD外分别与射线BA、AD、射线CD相切于点Q、R、N时.
类比图3可得,EQ=2,AQ=
∴BE= BA+ AQ-EQ =6+-2=
∴ t=,此时⊙P的半径为
学校:___________姓名:___________班级:___________考号:___________
题号
一
二
三
四
总分
得分
第I卷(选择题)
评卷人
得分
一、选择题
1.如图,已知为的直径,切于点A, 则下列结论不一定正确的是( )
A. B. C. D.
2.在Rt△ABC中,∠ C=90°,BC=1,AC=2,则tanA的值为( )
A.2 B. C. D.
3.如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为( )
A、1 B、 C、2 D、2
4.如图,已知BD是⊙O直径,点A、C在⊙O上, =,∠AOB=60°,则∠BDC的度数是( )
A.20° B.25° C.30° D. 40°
5.已知两圆的半径分别是2 cm和4 cm,圆心距是2cm,那么这两个圆的位置关系是( )
A.外离 B.外切 C.相交 D.内切
6.已知⊙O1、⊙O2的半径分别是,若两圆相交,则圆心距O1O2可能取的值是( )
A.2 B.4 C.6 D.8
7.在半径为R的圆内有长为R的弦,则此弦所对的圆周角是 ( )
A.30° B.60° C.30°或150° D.60°或120°
8.如图,小正方形的边长均为1,扇形OAB是某圆锥的侧面展开图,则这个圆锥的底面周长为( )
A. B. C.2 D.3
9.已知⊙O1和⊙O2相切,两圆的圆心距为10cm,⊙O1的半径为4cm,则⊙O2的半径为( ).
(A)3cm (B)6或14cm (C)2cm (D)4cm
10.已知半径分别为3 cm和1cm的两圆相交,则它们的圆心距可能是( )
A.1 cm B.3 cm C.5cm D.7cm
第II卷(非选择题)
评卷人
得分
二、填空题
11.在⊙O中,弦AB= 16cm,弦心距OC= 6cm,那么该圆的半径为 cm.
12.已知两圆的半径分别为2和3,两圆的圆心距为4,那么这两圆的位置关系是 .
13.直角三角形的两边长分别为16和12,则此三角形的外接圆半径是 .
14. 在直角坐标系中,以P(3,1)为圆心,r为半径的圆与坐标轴恰好有三个公共点,则r的值为 。
15.若扇形的圆心角为60°,弧长为2,则扇形的半径为 .
16.若等边三角形ABC的边长为cm,以点A为圆心,以3cm为半径作⊙A,则BC所在直线与⊙A的位置关系是_________.
评卷人
得分
三、计算题
17.如图,Rt△ABC中,∠C=Rt∠ , D是AB上一点,以BD为圆心的⊙O切AC于点E,交BC于点F ,OG⊥BC于G点。
(1)求证:CE=OG
(2)若BC=3 cm,sinB=, 求线段AD的长。
18.某玩具由一个圆形区域和一个扇形区域组成,如图,在和扇形中,与、分别相切于A、B,,E、F事直线与、扇形的两个交点,EF=24cm,设的半径为x cm,
① 用含x的代数式表示扇形的半径;
② 若和扇形两个区域的制作成本分别为0.45元和0.06元,当的半径为多少时,该玩具成本最小?
评卷人
得分
四、解答题
19.如图,AB是⊙O的直径,弦BC=2cm,∠ABC=60o.
(1)求⊙O的直径;
(2)若D是AB延长线上一点,连结CD,当BD长为多少时,CD与⊙O相切;
(3)若动点E以2cm/s的速度从A点出发沿着AB方向运动,同时动点F以1cm/s的速度从B点出发沿BC方向运动,设运动时间为,连结EF,当为何值时,△BEF为直角三角形.
如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D作DF⊥AB于点E,交O于点F,已知OE=1cm,DF=4cm.
20.求⊙O的半径
21.求切线CD的长
22.如图,已知⊙O的直径AB垂直于弦CD,垂足为E,F为CD延长线上一点,AF交⊙O于点G. 求证:AC2=AG·AF
已知:正方形ABCD的边长为2,⊙O交正方形ABCD的对角线AC所在直线于点T,连结TO交⊙O于点S,连结AS.
23.如图1,当⊙O经过A、D两点且圆心O在正方形ABCD内部时,连结DT、DS.
①试判断线段DT、DS的数量关系和位置关系; ②求AS+AT的值;
24.如图2,当⊙O经过A、D两点且圆心O在正方形ABCD外部时,连结DT、DS.求AS-AT的值;
25.如图3,延长DA到点E,使AE=AD,当⊙O经过A、E两点时,连结ET、ES.
根据(1)、(2)计算,通过观察、分析,对线段AS、AT的数量关系提出问题并解答.
26.推理证明:如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D过D作DE⊥BC,垂足为E,连结OE,CD=,∠ACB=30°.
(1)求证:DE是⊙O的切线;
(2)分别求AB,OE的长;
(3)填空:如果以点E为圆心,r为半径的圆上总存在不同的两点到点O的距离为1,则r的取值范围为 .
27.如图,PA 为⊙O的切线,B、D为⊙O上的两点,如果∠APB=,∠ADB=.(1)试判断直线PB与⊙O的位置关系,并说明理由;(2)如果D点是优弧AB上的一个动点,当且四边形ADBP是菱形时,求扇形OAMD的面积.
如图,矩形ABCD中,AB=6,BC=3.点E在线段BA上从B点以每秒1个单位的速度出发向A点运动,F是射线CD上一动点,在点E、F运动的过程中始终保持EF=5,且CF>BE,点P是EF的中点,连接AP.设点E运动时间为ts.
28.在点E运动过程中,AP的长度是如何变化的?( )
A.一直变短 B.一直变长 C.先变长后变短 D.先变短后变长
29.在点E、F运动的过程中,AP的长度存在一个最小值,当AP的长度取得最小值时,点P的位置应该在 .
30.以P为圆心作⊙P,当⊙P与矩形ABCD三边所在直线都相切时,求出此时t的值,并指出此时⊙P的半径长.
参考答案
1.D
2.B
3.D
4.C
5.D
6.B
7.C
8.B
9.B
10.B
11.10
12.相交。
13.8或10。
14.3或
15.6
16.相切
17.(1)证明:连接OE,
∵⊙O切AC于点E ∴∠OEC=900
∵∠ACB=∠CGO=Rt∠
∴四边形OGCE是矩形 ∴CE=OG
(2)解:在Rt△ABC中,sinB=
∴cosB=BC/AB=3/5
∵BC=3 ∴AB=BC÷cosB=3×5/3=5 cm
∵∠A=∠A , ∠AEO=∠ACB=Rt∠
∴△AEO∽△ACB
∴ 即
∴OB=
∴DO=2OB=
∴AD=AB-DB=5-=
18.解:(1)连接O1A。
∵⊙O1与O2C、O2D分别切一点A、B,
∴O1A⊥O2C,O2E平分∠CO2D。
∵,∴∠AO2O1=∠CO2D=30°。
在Rt△O1AO2中,,∴O1O2=A O1 sin∠AO2O1 =x sin30° =2x。
∵EF=24cm,∴FO2=EF-EO1-O1O2=24-3x,即扇形O2CD的半径为(24-3x)cm。
(2)设该玩具的制作成本为y元,则
。
∴当x=4时,y的值最小。
答:当⊙O1的半径为4cm时,该玩具的制作成本最小。
19.(1)4(2)
20.连接.
在中,直径弦于点,
cm.………………………………2分
在中,cm,cm,
(cm). ……………………………………4分
21.切于点,于点.
在与中,,,
. ……………………………………………………6分
,即.
(cm).
22.略
23.①线段DT、DS的数量和位置关系分别是DT=DS和DT⊥DS…2分
………3分
②证△DAS≌△DCT ……4分
∴AS+AT= …………5分
24.证△DAS≌△DCT …………6分
∴AS-AT= …………8分
25.提出的问题是:求 AT-AS 的值. …………10分
在TA上取TF=AS,连结EF,证△EAS≌△EFT …………11分
∴ AT-AS = …………12分
26.(1)见解析(2)2,(3)
27.⑴相切,理由:略⑵24π;
28.D
29.AD的中点
30.如图3,当⊙P在矩形ABCD内分别与AB、AD、CD相切于点Q、R、N时.
连接PQ、PR、PN,则PQ⊥AB、PR⊥AD、PN⊥CD
则四边形AQPR与四边形RPND为两个全等的正方形
∴PQ=AQ =AR=DR =AD=
在Rt△PQE中,EP=,由勾股定理可得:EQ=2
∴BE=BA-EQ-AQ=6-2-=
∴ t=,此时⊙P的半径为…
如图4,当⊙P在矩形ABCD外分别与射线BA、AD、射线CD相切于点Q、R、N时.
类比图3可得,EQ=2,AQ=
∴BE= BA+ AQ-EQ =6+-2=
∴ t=,此时⊙P的半径为
