2021--2022学年人教版七年级数学下册第八章二元一次方程组 复习课件 (共33张PPT)
文档属性
| 名称 | 2021--2022学年人教版七年级数学下册第八章二元一次方程组 复习课件 (共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 323.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-06 21:59:30 | ||
图片预览








文档简介
(共33张PPT)
二元一次方程组复习
二元
(三)元
一次
方程组
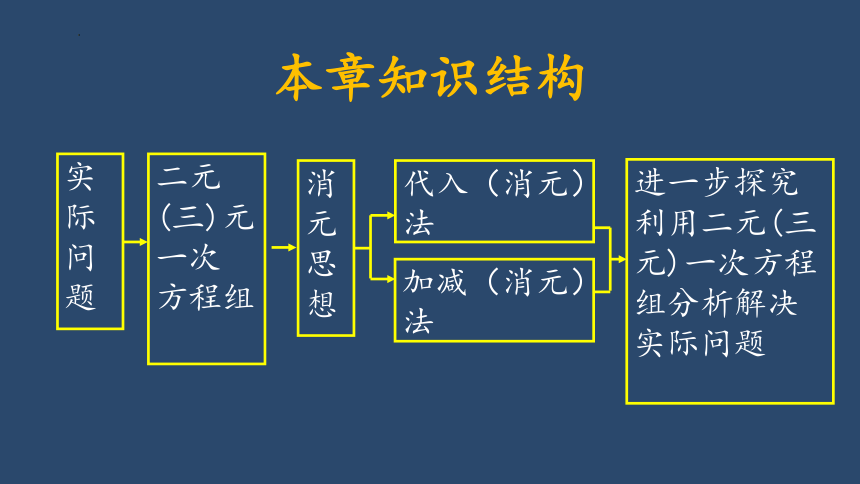
进一步探究利用二元(三元)一次方程组分析解决实际问题
实际问题
消元思想
代入(消元)法
加减(消元)法
本章知识结构
二元
(三)元
一次
方程组
进一步探究利用二元(三元)一次方程组分析解决实际问题
实际问题
消元思想
代入(消元)法
加减(消元)法
建立方程(组)解决问题的模型思想
解法以及问题转化中消元、化归的思想方法
知识回顾
有两个未知数且含未知数项的次数是一次的方程叫做二元一次方程.
知识点1、什么是二元一次方程?
适合一个二元一次方程的一对未知数的值,叫做这个二元一次方程的一个解.
一般地,在二元一次方程组中,使每个方程都适合的(公共解),叫做这个二元一次方程组的解.
知识点2、什么是二元一次方程组?
有两个一次方程组成,并且含有 两个未知数的方程组 叫做二元一次方程组.
什么是三元一次方程组?
知识回顾
3、用代入法解二元一次方程组时,关键要确定先消哪一个未知数.
当方程组的两个方程中某一方程的未知数系数是1的绝对值时,则优先选择此方程,用含另一个未知数的代数式来表示它,再代入另一个方程求解.
知识回顾
知识回顾
4、当方程组中两个方程的某个未知数的系数相等或互为相反数时,把方程的两边分别相减或相加来消去这个未知数,得到一个一元一次方程.
当方程组中两个未知数系数的绝对值均不相等,可以把两个方程的两边各自乘以一个适当的数,使某一个未知数的绝对值相等.
例 解下列方程组.
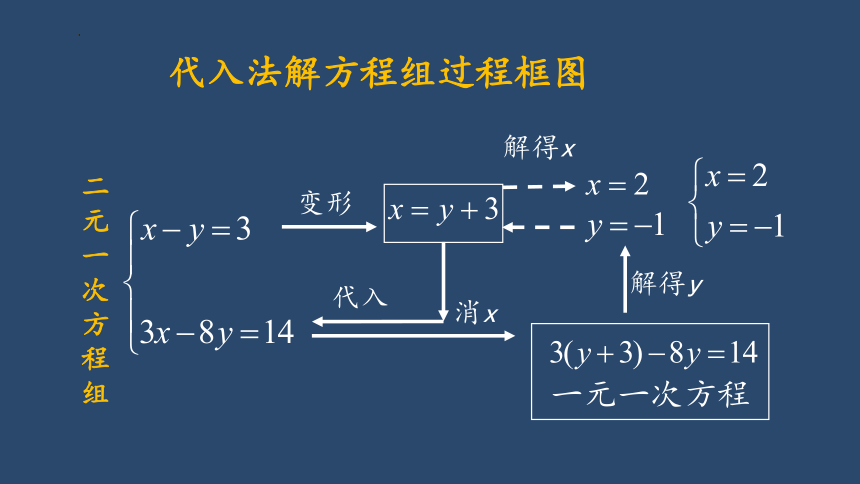
代入法解方程组过程框图
二元一次方程组
变形
代入
消x
一元一次方程
解得x
解得y
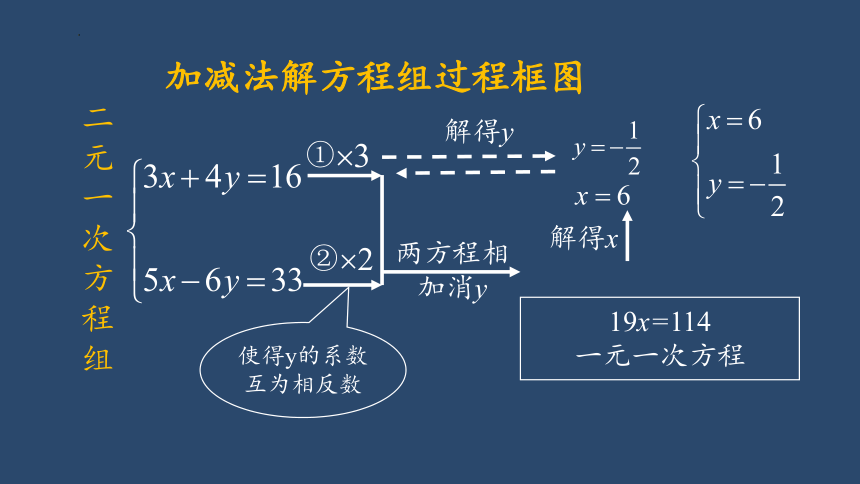
加减法解方程组过程框图
两方程相加消y
19x=114
一元一次方程
解得y
解得x
二元一次方程组
使得y的系数互为相反数
①
②
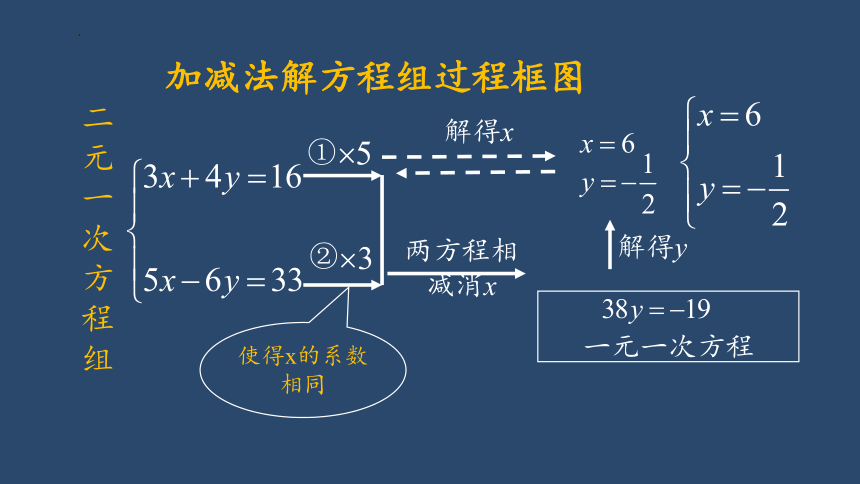
加减法解方程组过程框图
两方程相减消x
一元一次方程
解得x
解得y
使得x的系数相同
①
②
二元一次方程组
基本策略:化多为少,由繁至简,各个击破.
具体措施:代入法和加减法消元.
方法总结
1、方程x+2y=7在正整数范围内的解有( )
A 1个 B 2个 C 3个 D 无数个
C
解后语:二元一次方程一般有无数个解,但它的解若受到限制往往是有限个解.
学以致用
2、若x2m-1+5y3n-2m=7是二元一次方程,则m= ,n= ,
1
1
解后语:二元一次方程要求含有未知数项的次数都是1,同时未知数项的系数不能为零.
学以致用
解:
①
②
所以
把③代入① ,得
把 代入③ ,得
所以这个方程组的解是
③
① ② ,得
学以致用
既要有按照解法步骤进行求解的好习惯, 又应有多观察、勤思考,灵活运用多种方式去消元的意识.
方法总结
应用二元一次方程解实际问题的步骤:
审清题意
(找出等量关系)
设未知数
列方程
解方程
检验解的合理性
作答
知识回顾
《九章算术》是中国传统数学最重要的著作,其中“方程术”是《九章算术》最高的数学成就. 其中记载:
“今有牛五、羊二,直金十两;牛二、羊五,直金
八两. 问牛、羊各直金几何?”
典例分析
译文:“有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两. 问每头牛、每只羊各值金多少两?”
典例分析
等量关系:
5头牛、2只羊, 值金10两;
2头牛、5只羊, 值金8两.
解:设每头牛值金 x 两, 每只羊值金 y 两.
可列方程组
典例分析
建立方程的关键是把已知量和未知量联系起来,找出题目中的等量关系,分析等量关系.
方法总结
从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.甲地到乙地全程是多少?
学以致用
平路
上坡
甲地
乙地
上坡每小时走3km
平路每小时走4km
平路
平路每小时走4km
下坡
下坡每小时走5km
画出图形辅助理解题意
从甲地到乙地 需54min 上坡时间= 平路时间=
从乙地到甲地 需42min 下坡时间= 平路时间=
画出表格梳理关系
坡路路程
平路路程
坡路路程
上坡速度
坡路路程
下坡速度
平路路程
平路速度
平路路程
平路速度
+
=
从甲地到乙地时间
+
=
从乙地到甲地时间
等量关系:
注意方程两边单位统一
解:设坡路长 km 平路长 km 则列方程组为
解得
答:从甲地到乙地全程3.1km.
∴
当具体问题中除了要求的未知量还存在隐含的未知量,寻找等量关系,找到隐含未知量也是关键.
方法总结
1、-1=3y 是不是二元一次方程?答: (“是”或者“不是”)
不是
无数
-1
提高训练
3、方程3x + 2y =1中,当x =1时,y = .
2、方程3x – y =1有 个解.
4、若 是方程3x + y – k =1的一个解,则k=
5、已知方程①2x + y =0,②x + 2y =3,那么能满足的方程是 (用数字①、②填空)
①、②
2
提高训练
6、已知y=kx+b,如果x=4时,y=15;x=7时,y=24,则k= ;b= .
当X=4,y=15 15=4k+b
当X=7,y=24 24=7x+b
解得:
提高训练
3
3
分析:
7、在y=ax +bx=c中,当x=0时y的值是-7,x=1时y的值是-9, x=-1时y的值是-3,求a、b、c的值.
当x=0 y=7 -7=c
当x=1 y=-9 -9=a+b+c
当x=-1 y=-3 -3=a-b+c
解得:
提高训练
小结:
1.列方程组解决问题的意识.
2.发现隐含的未知数,恰当设未知数.
3.分析数量关系、找到等量关系列出方程组.
方法总结
谢谢
二元一次方程组复习
二元
(三)元
一次
方程组
进一步探究利用二元(三元)一次方程组分析解决实际问题
实际问题
消元思想
代入(消元)法
加减(消元)法
本章知识结构
二元
(三)元
一次
方程组
进一步探究利用二元(三元)一次方程组分析解决实际问题
实际问题
消元思想
代入(消元)法
加减(消元)法
建立方程(组)解决问题的模型思想
解法以及问题转化中消元、化归的思想方法
知识回顾
有两个未知数且含未知数项的次数是一次的方程叫做二元一次方程.
知识点1、什么是二元一次方程?
适合一个二元一次方程的一对未知数的值,叫做这个二元一次方程的一个解.
一般地,在二元一次方程组中,使每个方程都适合的(公共解),叫做这个二元一次方程组的解.
知识点2、什么是二元一次方程组?
有两个一次方程组成,并且含有 两个未知数的方程组 叫做二元一次方程组.
什么是三元一次方程组?
知识回顾
3、用代入法解二元一次方程组时,关键要确定先消哪一个未知数.
当方程组的两个方程中某一方程的未知数系数是1的绝对值时,则优先选择此方程,用含另一个未知数的代数式来表示它,再代入另一个方程求解.
知识回顾
知识回顾
4、当方程组中两个方程的某个未知数的系数相等或互为相反数时,把方程的两边分别相减或相加来消去这个未知数,得到一个一元一次方程.
当方程组中两个未知数系数的绝对值均不相等,可以把两个方程的两边各自乘以一个适当的数,使某一个未知数的绝对值相等.
例 解下列方程组.
代入法解方程组过程框图
二元一次方程组
变形
代入
消x
一元一次方程
解得x
解得y
加减法解方程组过程框图
两方程相加消y
19x=114
一元一次方程
解得y
解得x
二元一次方程组
使得y的系数互为相反数
①
②
加减法解方程组过程框图
两方程相减消x
一元一次方程
解得x
解得y
使得x的系数相同
①
②
二元一次方程组
基本策略:化多为少,由繁至简,各个击破.
具体措施:代入法和加减法消元.
方法总结
1、方程x+2y=7在正整数范围内的解有( )
A 1个 B 2个 C 3个 D 无数个
C
解后语:二元一次方程一般有无数个解,但它的解若受到限制往往是有限个解.
学以致用
2、若x2m-1+5y3n-2m=7是二元一次方程,则m= ,n= ,
1
1
解后语:二元一次方程要求含有未知数项的次数都是1,同时未知数项的系数不能为零.
学以致用
解:
①
②
所以
把③代入① ,得
把 代入③ ,得
所以这个方程组的解是
③
① ② ,得
学以致用
既要有按照解法步骤进行求解的好习惯, 又应有多观察、勤思考,灵活运用多种方式去消元的意识.
方法总结
应用二元一次方程解实际问题的步骤:
审清题意
(找出等量关系)
设未知数
列方程
解方程
检验解的合理性
作答
知识回顾
《九章算术》是中国传统数学最重要的著作,其中“方程术”是《九章算术》最高的数学成就. 其中记载:
“今有牛五、羊二,直金十两;牛二、羊五,直金
八两. 问牛、羊各直金几何?”
典例分析
译文:“有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两. 问每头牛、每只羊各值金多少两?”
典例分析
等量关系:
5头牛、2只羊, 值金10两;
2头牛、5只羊, 值金8两.
解:设每头牛值金 x 两, 每只羊值金 y 两.
可列方程组
典例分析
建立方程的关键是把已知量和未知量联系起来,找出题目中的等量关系,分析等量关系.
方法总结
从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.甲地到乙地全程是多少?
学以致用
平路
上坡
甲地
乙地
上坡每小时走3km
平路每小时走4km
平路
平路每小时走4km
下坡
下坡每小时走5km
画出图形辅助理解题意
从甲地到乙地 需54min 上坡时间= 平路时间=
从乙地到甲地 需42min 下坡时间= 平路时间=
画出表格梳理关系
坡路路程
平路路程
坡路路程
上坡速度
坡路路程
下坡速度
平路路程
平路速度
平路路程
平路速度
+
=
从甲地到乙地时间
+
=
从乙地到甲地时间
等量关系:
注意方程两边单位统一
解:设坡路长 km 平路长 km 则列方程组为
解得
答:从甲地到乙地全程3.1km.
∴
当具体问题中除了要求的未知量还存在隐含的未知量,寻找等量关系,找到隐含未知量也是关键.
方法总结
1、-1=3y 是不是二元一次方程?答: (“是”或者“不是”)
不是
无数
-1
提高训练
3、方程3x + 2y =1中,当x =1时,y = .
2、方程3x – y =1有 个解.
4、若 是方程3x + y – k =1的一个解,则k=
5、已知方程①2x + y =0,②x + 2y =3,那么能满足的方程是 (用数字①、②填空)
①、②
2
提高训练
6、已知y=kx+b,如果x=4时,y=15;x=7时,y=24,则k= ;b= .
当X=4,y=15 15=4k+b
当X=7,y=24 24=7x+b
解得:
提高训练
3
3
分析:
7、在y=ax +bx=c中,当x=0时y的值是-7,x=1时y的值是-9, x=-1时y的值是-3,求a、b、c的值.
当x=0 y=7 -7=c
当x=1 y=-9 -9=a+b+c
当x=-1 y=-3 -3=a-b+c
解得:
提高训练
小结:
1.列方程组解决问题的意识.
2.发现隐含的未知数,恰当设未知数.
3.分析数量关系、找到等量关系列出方程组.
方法总结
谢谢
