2022年春人教版七年级数学下册 第九章 不等式与不等式组 测试卷(word版含解析 )
文档属性
| 名称 | 2022年春人教版七年级数学下册 第九章 不等式与不等式组 测试卷(word版含解析 ) |

|
|
| 格式 | zip | ||
| 文件大小 | 263.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 00:00:00 | ||
图片预览




文档简介
人教版七年级数学下册第九章测试卷
一、选择题:(每小题3分,共36分)
1. 以下所给数值中,为不等式﹣2x+3<0的解的是( )
A. ﹣2 B. ﹣1 C. D. 2
2. 下列式子中,是不等式有( ).
①2x=7;②3x+4y;③-3<2;④2a-3≥0;⑤x>1;⑥a-b>1.
A. 5个 B. 4个
C. 3个 D. 1个
3. 若a<b,则下列各式正确的是( )
A. 3a>3b B. ﹣3a>﹣3b C. a﹣3>b﹣3 D.
4. 不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
5. 把不等式组 的解集在数轴上表示,正确的结果是( )
A. B.
C. D.
6. “x与y的和的不大于7”用不等式表示为( ).
A. (x+y)<7 B. (x+y)>7
C. x+y≤7 D. (x+y)≤7
7. 不等式组最小整数解是( )
A. -1 B. 0 C. 2 D. 3
8. 下列说法错误的是( ).
A. 不等式x-3>2的解集是x>5 B. 不等式x<3的整数解有无数个
C. x=0是不等式2x<3的一个解 D. 不等式x+3<3的整数解是0
9. 在平面直角坐标系中,若点P在第四象限,则的取值范围是( )
A >1 B. <2 C. 1<<2 D. 无解
10. 不等式-5<2x≤4的所有整数解的代数和是( ).
A 2 B. 0 C. -2 D. -5
11. 已知关于的不等式组的整数解共有5个,则的取值范围是( ).
A. -3<<-2 B. -3<≤-2 C. -3≤≤-2 D. -3≤<-2
12. 若不等式组有解,则的取值范围是( )
A. B. C. D.
二、填空题(每小题3分,共18分)
13. 不等式的正整数解是____________.
14. 的最小值是a,的最大值是b,则 ______
15. 把关于的不等式组的解集表示在数轴上,如图所示,那么这个不等式组的解集是___________.
16. 若不等式组无解,则ab的大小关系是__________.
17. 若代数式的值不小于代数式的值,则x的取值范围是_______.
18. 如果不等式组的解集是,那么的值为__________.
三、解答题(本大题共6个小题,共46分)
19. 解不等式,并把解集在数轴上表示出来:
20. 解不等式组,并把解集在数轴上表示出来.
21. 如果关于x的方程-2x=4-a的解大于关于x的方程a(x-1)=x(a-2)的解,求a的取值范围.
22. 已知方程组的解x,y的和是负数,求满足条件的最小整数a.
23. 已知一件文化衫价格为18元,一个书包的价格比一件文化衫价格的2倍还少6元.
(1)求一个书包的价格是多少元?
(2)某公司出资1 800元,拿出不少于350元但不超过400元的经费奖励山区小学的优秀学生,剩余经费还能为多少名山区小学的学生每人购买一个书包和一件文化衫?
24. 某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.
(1)该校初三年级共有多少人参加春游?
(2)请你帮该校设计一种最省钱的租车方案.
人教版七年级数学下册第九章测试卷(解析版)
一、选择题:(每小题3分,共36分)
1. 以下所给的数值中,为不等式﹣2x+3<0的解的是( )
A. ﹣2 B. ﹣1 C. D. 2
【1题答案】
【答案】D
【解析】
【详解】解:-2x<-3,x>,∴不等式的解集是:x>.故选D.
2. 下列式子中,是不等式的有( ).
①2x=7;②3x+4y;③-3<2;④2a-3≥0;⑤x>1;⑥a-b>1.
A. 5个 B. 4个
C 3个 D. 1个
【2题答案】
【答案】B
【解析】
【详解】解:不等式有:③-3<2;④2a-3≥0;⑤x>1;⑥a-b>1,共4个.故选B.
3. 若a<b,则下列各式正确的是( )
A. 3a>3b B. ﹣3a>﹣3b C. a﹣3>b﹣3 D.
【3题答案】
【答案】B
【解析】
【详解】解:A.∵a<b,∴3a<3b,故本选项错误;
B.∵a<b,∴﹣a>﹣b,∴﹣3a>﹣3b,故本选项正确;
C.∵a<b,∴a﹣3<b﹣3,故本选项错误;
D.∵a<b,∴,故本选项错误.
故选B.
点睛:本题考查的是不等式的性质,熟知不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变是解答此题的关键.
4. 不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
【4题答案】
【答案】B
【解析】
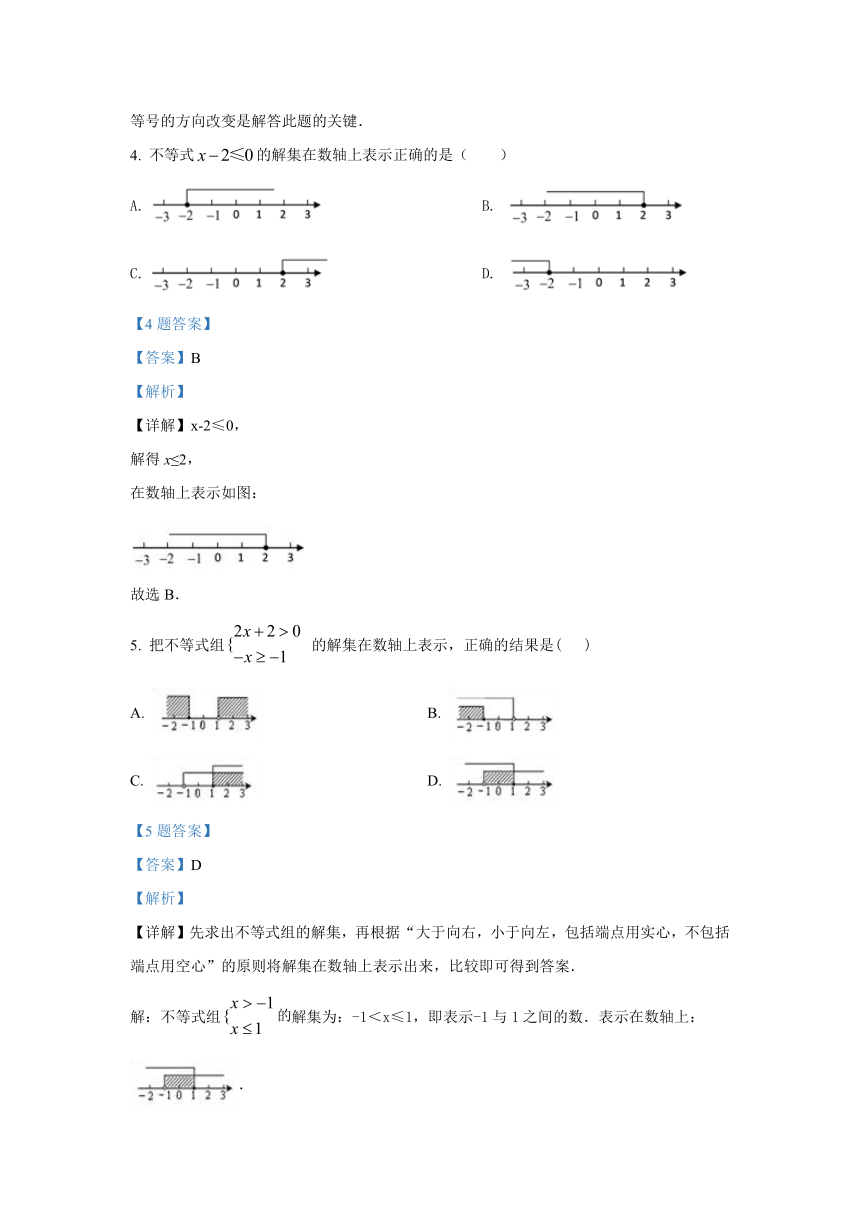
【详解】x-2≤0,
解得x≤2,
在数轴上表示如图:
故选B.
5. 把不等式组 的解集在数轴上表示,正确的结果是( )
A. B.
C. D.
【5题答案】
【答案】D
【解析】
【详解】先求出不等式组的解集,再根据“大于向右,小于向左,包括端点用实心,不包括端点用空心”的原则将解集在数轴上表示出来,比较即可得到答案.
解:不等式组解集为:-1<x≤1,即表示-1与1之间的数.表示在数轴上:
.
故选D.
“点睛”不等式组解集在数轴上的表示方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
6. “x与y的和的不大于7”用不等式表示为( ).
A. (x+y)<7 B. (x+y)>7
C. x+y≤7 D. (x+y)≤7
【6题答案】
【答案】D
【解析】
【详解】解:“x与y的和的不大于7”用不等式表示为.故选D.
7. 不等式组的最小整数解是( )
A. -1 B. 0 C. 2 D. 3
【7题答案】
【答案】A
【解析】
【详解】解:解不等式2x>-3可得x>-,
解不等式x-1≤8-2x可得x≤3,
根据不等式的解集的确定:都大取大,都小取小,大小小大取中间,大大小小无解,可得不等式组的解集为-<x≤3,
所以整数解:-1,0,1,2,3,最小整数解为-1.
故选A.
8. 下列说法错误的是( ).
A. 不等式x-3>2的解集是x>5 B. 不等式x<3的整数解有无数个
C. x=0是不等式2x<3的一个解 D. 不等式x+3<3的整数解是0
【8题答案】
【答案】D
【解析】
【详解】解:A. 不等式x-3>2的解集是x>5,正确;
B. 不等式x<3的整数解有无数个,正确;
C. x=0是不等式2x<3的一个解,正确;
D. 不等式x+3<3的解集是x<0,故D选项错误.
故选D.
9. 在平面直角坐标系中,若点P在第四象限,则的取值范围是( )
A. >1 B. <2 C. 1<<2 D. 无解
【9题答案】
【答案】C
【解析】
【详解】解:由点P(x﹣1,2x﹣4)在第四象限,得:,解得:1<x<2,故选C.
点睛:本题考查了各象限内点坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解题的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
10. 不等式-5<2x≤4的所有整数解的代数和是( ).
A. 2 B. 0 C. -2 D. -5
【10题答案】
【答案】B
【解析】
【详解】解:-5<2x≤4,∴-2.5<x≤2,整数解为:-2,-1,0,1,2.故整数解的和为0.故选B.
11. 已知关于的不等式组的整数解共有5个,则的取值范围是( ).
A. -3<<-2 B. -3<≤-2 C. -3≤≤-2 D. -3≤<-2
【11题答案】
【答案】B
【解析】
【详解】解: ,∵解不等式①得:x≥a,解不等式②得:x<3,
∴不等式组的解集为a≤x<3.
∵关于x的不等式组 的整数解共有5个,它们是2,1,0,-1,-2,∴-3<a≤-2,故选B.
点睛:本题考查了解一元一次不等式组,不等式组的整数解的应用,解答此题的关键是能根据不等式组的解集和已知得出关于a的不等式组.
12. 若不等式组有解,则的取值范围是( )
A. B. C. D.
【12题答案】
【答案】A
【解析】
【分析】先求出两个不等式的解集,再根据已知得出关于a的不等式,求出不等式的解集即可.
【详解】解:
由①得:
由②得:
不等式组有解,
故选
【点睛】本题考查了解一元一次不等式,解一元一次不等式组的应用,解此题的关键是得出关于a的不等式.
二、填空题(每小题3分,共18分)
13. 不等式的正整数解是____________.
【13题答案】
【答案】1、2、3
【解析】
【详解】解:3x≤10,x≤,∴正整数解为:1,2,3.故答案为1,2,3.
14. 的最小值是a,的最大值是b,则 ______
【14题答案】
【答案】-4
【解析】
【详解】分析:解答此题要理解“≥”“≤”的意义,判断出a和b的最值即可解答.
详解:因为x≥2的最小值是a,∴a=2;
x≤﹣6的最大值是b,∴b=﹣6;
则a+b=2﹣6=﹣4,所以a+b=﹣4.
故答案为﹣4.
点睛:解答此题要明确,x≥2时,x可以等于2;x≤﹣6时,x可以等于﹣6.
15. 把关于的不等式组的解集表示在数轴上,如图所示,那么这个不等式组的解集是___________.
【15题答案】
【答案】
【解析】
【详解】解:由图可知:x>1.故答案为x>1.
16. 若不等式组无解,则ab的大小关系是__________.
【16题答案】
【答案】b≥a
【解析】
【分析】根据求不等式组解集的方法:“大大小小找不到(无解)”求解可得.
【详解】解:∵不等式组无解,
∴b≥a,
故答案为:b≥a.
【点睛】本题主要考查了不等式组的解集,解题时注意:不等式组中两个不等式的解集无公共部分,则不等式组无解.
17. 若代数式的值不小于代数式的值,则x的取值范围是_______.
【17题答案】
【答案】
【解析】
【详解】解:由题意得:,解得:x≥3.故答案为x≥3.
18. 如果不等式组的解集是,那么的值为__________.
【18题答案】
【答案】1
【解析】
【详解】解:不等式组的解集为4﹣2a≤x<,∵它的解集是0≤x<1,∴4﹣2a=0,=1,解得:a=2,b=﹣1,∴=1.故答案为1.
点睛:本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).
三、解答题(本大题共6个小题,共46分)
19. 解不等式,并把解集在数轴上表示出来:
【19题答案】
【答案】,数轴表示见解析.
【解析】
【详解】试题分析:不等式去括号、移项、合并同类项,化系数为1即可.
试题解析:解: 去括号得:2+6x<3
移项,合并得:6x<1
解得:.
数轴表示为:
20. 解不等式组,并把解集在数轴上表示出来.
【20题答案】
【答案】
【解析】
【分析】解一元一次不等式组,先求出不等式组中每一个不等式的解集,再利用口诀求出这些解集的公共部分:同大取大,同小取小,大小小大中间找,大大小小解不了(无解).
【详解】解:由,得; 由,得.
∴原不等式组的解为.
在数轴上表示这个解集如图所示:
【点睛】
不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
21. 如果关于x的方程-2x=4-a的解大于关于x的方程a(x-1)=x(a-2)的解,求a的取值范围.
【21题答案】
【答案】a>12
【解析】
【详解】试题分析:先求出两个方程的解,然后列出不等式,求解不等式即可.
试题解析:解:解方程,得:x=.
解方程a(x-1)=x(a-2),得:x=.
由题意得:>
解得:a>12.
点睛:本题考查了解一元一次不等式和一元一次方程的解,解答本题的关键是掌握不等式的性质.
22. 已知方程组的解x,y的和是负数,求满足条件的最小整数a.
【22题答案】
【答案】1
【解析】
【详解】试题分析:把a当作已知数,解方程组求出方程组的解(x y的值),根据已知得出不等式,求出a的取值范围即可.
试题解析:解:解方程组,得:.
依题意,得:,解得:a>,所以满足条件的最小整数a为1.
点睛:本题综合考查了解方程组和解不等式的应用,关键是根据题意求出关于a的不等式.
23. 已知一件文化衫价格为18元,一个书包的价格比一件文化衫价格的2倍还少6元.
(1)求一个书包的价格是多少元?
(2)某公司出资1 800元,拿出不少于350元但不超过400元的经费奖励山区小学的优秀学生,剩余经费还能为多少名山区小学的学生每人购买一个书包和一件文化衫?
【23题答案】
【答案】(1)30元;(2)30名
【解析】
【详解】试题分析:(1)书包的价格=文化衫×2﹣6,据此列式即可求解.
(2)不等关系为:
350≤1800元﹣每人购买一个书包和一件文化衫的价钱≤400,列不等式组,求解取正整数值即可.
试题解析:解:(1)18×2﹣6=30(元),所以一个书包的价格是30元.
(2)设还能为x名学生每人购买一个书包和一件文化衫,根据题意得:
350≤1 800-(18+30)x≤400.
解得:.
∵x为正整数,∴x=30.
答:剩余经费还能为30名学生每人购买一个书包和一件文化衫.
点睛:解决本题关键是读懂题意,找到所求量的等量关系及符合题意的不等关系式组.
24.
某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.
(1)该校初三年级共有多少人参加春游?
(2)请你帮该校设计一种最省钱的租车方案.
【24题答案】
【答案】(1)288
(2)租42座车6辆和36座车1辆最省钱
【解析】
【分析】(1)设租36座的车辆,则租42座的客车辆.
不等关系:租42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人.
(2)根据(1)中求得的人数,进一步计算三种方案的费用:①只租36座客车;②只租42座客车;③合租两种车.再进一步比较得到结论即可.
【详解】解:(1)设租36座的车辆.
据题意得:,
解得:.
.
是整数,
.
则春游人数为:(人.
(2)方案①:租36座车8辆的费用:元;
方案②:租42座车7辆的费用:元;
方案③:,
座车越多越省钱,
又,余下人数正好36座,可以得出:租42座车6辆和36座车1辆的总费用:元.
,
方案③:租42座车6辆和36座车1辆最省钱.
【点睛】本题考查了不等关系,解题的关键是特别注意要能够分别求得每一种方案的价钱,再作比较。
一、选择题:(每小题3分,共36分)
1. 以下所给数值中,为不等式﹣2x+3<0的解的是( )
A. ﹣2 B. ﹣1 C. D. 2
2. 下列式子中,是不等式有( ).
①2x=7;②3x+4y;③-3<2;④2a-3≥0;⑤x>1;⑥a-b>1.
A. 5个 B. 4个
C. 3个 D. 1个
3. 若a<b,则下列各式正确的是( )
A. 3a>3b B. ﹣3a>﹣3b C. a﹣3>b﹣3 D.
4. 不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
5. 把不等式组 的解集在数轴上表示,正确的结果是( )
A. B.
C. D.
6. “x与y的和的不大于7”用不等式表示为( ).
A. (x+y)<7 B. (x+y)>7
C. x+y≤7 D. (x+y)≤7
7. 不等式组最小整数解是( )
A. -1 B. 0 C. 2 D. 3
8. 下列说法错误的是( ).
A. 不等式x-3>2的解集是x>5 B. 不等式x<3的整数解有无数个
C. x=0是不等式2x<3的一个解 D. 不等式x+3<3的整数解是0
9. 在平面直角坐标系中,若点P在第四象限,则的取值范围是( )
A >1 B. <2 C. 1<<2 D. 无解
10. 不等式-5<2x≤4的所有整数解的代数和是( ).
A 2 B. 0 C. -2 D. -5
11. 已知关于的不等式组的整数解共有5个,则的取值范围是( ).
A. -3<<-2 B. -3<≤-2 C. -3≤≤-2 D. -3≤<-2
12. 若不等式组有解,则的取值范围是( )
A. B. C. D.
二、填空题(每小题3分,共18分)
13. 不等式的正整数解是____________.
14. 的最小值是a,的最大值是b,则 ______
15. 把关于的不等式组的解集表示在数轴上,如图所示,那么这个不等式组的解集是___________.
16. 若不等式组无解,则ab的大小关系是__________.
17. 若代数式的值不小于代数式的值,则x的取值范围是_______.
18. 如果不等式组的解集是,那么的值为__________.
三、解答题(本大题共6个小题,共46分)
19. 解不等式,并把解集在数轴上表示出来:
20. 解不等式组,并把解集在数轴上表示出来.
21. 如果关于x的方程-2x=4-a的解大于关于x的方程a(x-1)=x(a-2)的解,求a的取值范围.
22. 已知方程组的解x,y的和是负数,求满足条件的最小整数a.
23. 已知一件文化衫价格为18元,一个书包的价格比一件文化衫价格的2倍还少6元.
(1)求一个书包的价格是多少元?
(2)某公司出资1 800元,拿出不少于350元但不超过400元的经费奖励山区小学的优秀学生,剩余经费还能为多少名山区小学的学生每人购买一个书包和一件文化衫?
24. 某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.
(1)该校初三年级共有多少人参加春游?
(2)请你帮该校设计一种最省钱的租车方案.
人教版七年级数学下册第九章测试卷(解析版)
一、选择题:(每小题3分,共36分)
1. 以下所给的数值中,为不等式﹣2x+3<0的解的是( )
A. ﹣2 B. ﹣1 C. D. 2
【1题答案】
【答案】D
【解析】
【详解】解:-2x<-3,x>,∴不等式的解集是:x>.故选D.
2. 下列式子中,是不等式的有( ).
①2x=7;②3x+4y;③-3<2;④2a-3≥0;⑤x>1;⑥a-b>1.
A. 5个 B. 4个
C 3个 D. 1个
【2题答案】
【答案】B
【解析】
【详解】解:不等式有:③-3<2;④2a-3≥0;⑤x>1;⑥a-b>1,共4个.故选B.
3. 若a<b,则下列各式正确的是( )
A. 3a>3b B. ﹣3a>﹣3b C. a﹣3>b﹣3 D.
【3题答案】
【答案】B
【解析】
【详解】解:A.∵a<b,∴3a<3b,故本选项错误;
B.∵a<b,∴﹣a>﹣b,∴﹣3a>﹣3b,故本选项正确;
C.∵a<b,∴a﹣3<b﹣3,故本选项错误;
D.∵a<b,∴,故本选项错误.
故选B.
点睛:本题考查的是不等式的性质,熟知不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变是解答此题的关键.
4. 不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
【4题答案】
【答案】B
【解析】
【详解】x-2≤0,
解得x≤2,
在数轴上表示如图:
故选B.
5. 把不等式组 的解集在数轴上表示,正确的结果是( )
A. B.
C. D.
【5题答案】
【答案】D
【解析】
【详解】先求出不等式组的解集,再根据“大于向右,小于向左,包括端点用实心,不包括端点用空心”的原则将解集在数轴上表示出来,比较即可得到答案.
解:不等式组解集为:-1<x≤1,即表示-1与1之间的数.表示在数轴上:
.
故选D.
“点睛”不等式组解集在数轴上的表示方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
6. “x与y的和的不大于7”用不等式表示为( ).
A. (x+y)<7 B. (x+y)>7
C. x+y≤7 D. (x+y)≤7
【6题答案】
【答案】D
【解析】
【详解】解:“x与y的和的不大于7”用不等式表示为.故选D.
7. 不等式组的最小整数解是( )
A. -1 B. 0 C. 2 D. 3
【7题答案】
【答案】A
【解析】
【详解】解:解不等式2x>-3可得x>-,
解不等式x-1≤8-2x可得x≤3,
根据不等式的解集的确定:都大取大,都小取小,大小小大取中间,大大小小无解,可得不等式组的解集为-<x≤3,
所以整数解:-1,0,1,2,3,最小整数解为-1.
故选A.
8. 下列说法错误的是( ).
A. 不等式x-3>2的解集是x>5 B. 不等式x<3的整数解有无数个
C. x=0是不等式2x<3的一个解 D. 不等式x+3<3的整数解是0
【8题答案】
【答案】D
【解析】
【详解】解:A. 不等式x-3>2的解集是x>5,正确;
B. 不等式x<3的整数解有无数个,正确;
C. x=0是不等式2x<3的一个解,正确;
D. 不等式x+3<3的解集是x<0,故D选项错误.
故选D.
9. 在平面直角坐标系中,若点P在第四象限,则的取值范围是( )
A. >1 B. <2 C. 1<<2 D. 无解
【9题答案】
【答案】C
【解析】
【详解】解:由点P(x﹣1,2x﹣4)在第四象限,得:,解得:1<x<2,故选C.
点睛:本题考查了各象限内点坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解题的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
10. 不等式-5<2x≤4的所有整数解的代数和是( ).
A. 2 B. 0 C. -2 D. -5
【10题答案】
【答案】B
【解析】
【详解】解:-5<2x≤4,∴-2.5<x≤2,整数解为:-2,-1,0,1,2.故整数解的和为0.故选B.
11. 已知关于的不等式组的整数解共有5个,则的取值范围是( ).
A. -3<<-2 B. -3<≤-2 C. -3≤≤-2 D. -3≤<-2
【11题答案】
【答案】B
【解析】
【详解】解: ,∵解不等式①得:x≥a,解不等式②得:x<3,
∴不等式组的解集为a≤x<3.
∵关于x的不等式组 的整数解共有5个,它们是2,1,0,-1,-2,∴-3<a≤-2,故选B.
点睛:本题考查了解一元一次不等式组,不等式组的整数解的应用,解答此题的关键是能根据不等式组的解集和已知得出关于a的不等式组.
12. 若不等式组有解,则的取值范围是( )
A. B. C. D.
【12题答案】
【答案】A
【解析】
【分析】先求出两个不等式的解集,再根据已知得出关于a的不等式,求出不等式的解集即可.
【详解】解:
由①得:
由②得:
不等式组有解,
故选
【点睛】本题考查了解一元一次不等式,解一元一次不等式组的应用,解此题的关键是得出关于a的不等式.
二、填空题(每小题3分,共18分)
13. 不等式的正整数解是____________.
【13题答案】
【答案】1、2、3
【解析】
【详解】解:3x≤10,x≤,∴正整数解为:1,2,3.故答案为1,2,3.
14. 的最小值是a,的最大值是b,则 ______
【14题答案】
【答案】-4
【解析】
【详解】分析:解答此题要理解“≥”“≤”的意义,判断出a和b的最值即可解答.
详解:因为x≥2的最小值是a,∴a=2;
x≤﹣6的最大值是b,∴b=﹣6;
则a+b=2﹣6=﹣4,所以a+b=﹣4.
故答案为﹣4.
点睛:解答此题要明确,x≥2时,x可以等于2;x≤﹣6时,x可以等于﹣6.
15. 把关于的不等式组的解集表示在数轴上,如图所示,那么这个不等式组的解集是___________.
【15题答案】
【答案】
【解析】
【详解】解:由图可知:x>1.故答案为x>1.
16. 若不等式组无解,则ab的大小关系是__________.
【16题答案】
【答案】b≥a
【解析】
【分析】根据求不等式组解集的方法:“大大小小找不到(无解)”求解可得.
【详解】解:∵不等式组无解,
∴b≥a,
故答案为:b≥a.
【点睛】本题主要考查了不等式组的解集,解题时注意:不等式组中两个不等式的解集无公共部分,则不等式组无解.
17. 若代数式的值不小于代数式的值,则x的取值范围是_______.
【17题答案】
【答案】
【解析】
【详解】解:由题意得:,解得:x≥3.故答案为x≥3.
18. 如果不等式组的解集是,那么的值为__________.
【18题答案】
【答案】1
【解析】
【详解】解:不等式组的解集为4﹣2a≤x<,∵它的解集是0≤x<1,∴4﹣2a=0,=1,解得:a=2,b=﹣1,∴=1.故答案为1.
点睛:本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).
三、解答题(本大题共6个小题,共46分)
19. 解不等式,并把解集在数轴上表示出来:
【19题答案】
【答案】,数轴表示见解析.
【解析】
【详解】试题分析:不等式去括号、移项、合并同类项,化系数为1即可.
试题解析:解: 去括号得:2+6x<3
移项,合并得:6x<1
解得:.
数轴表示为:
20. 解不等式组,并把解集在数轴上表示出来.
【20题答案】
【答案】
【解析】
【分析】解一元一次不等式组,先求出不等式组中每一个不等式的解集,再利用口诀求出这些解集的公共部分:同大取大,同小取小,大小小大中间找,大大小小解不了(无解).
【详解】解:由,得; 由,得.
∴原不等式组的解为.
在数轴上表示这个解集如图所示:
【点睛】
不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
21. 如果关于x的方程-2x=4-a的解大于关于x的方程a(x-1)=x(a-2)的解,求a的取值范围.
【21题答案】
【答案】a>12
【解析】
【详解】试题分析:先求出两个方程的解,然后列出不等式,求解不等式即可.
试题解析:解:解方程,得:x=.
解方程a(x-1)=x(a-2),得:x=.
由题意得:>
解得:a>12.
点睛:本题考查了解一元一次不等式和一元一次方程的解,解答本题的关键是掌握不等式的性质.
22. 已知方程组的解x,y的和是负数,求满足条件的最小整数a.
【22题答案】
【答案】1
【解析】
【详解】试题分析:把a当作已知数,解方程组求出方程组的解(x y的值),根据已知得出不等式,求出a的取值范围即可.
试题解析:解:解方程组,得:.
依题意,得:,解得:a>,所以满足条件的最小整数a为1.
点睛:本题综合考查了解方程组和解不等式的应用,关键是根据题意求出关于a的不等式.
23. 已知一件文化衫价格为18元,一个书包的价格比一件文化衫价格的2倍还少6元.
(1)求一个书包的价格是多少元?
(2)某公司出资1 800元,拿出不少于350元但不超过400元的经费奖励山区小学的优秀学生,剩余经费还能为多少名山区小学的学生每人购买一个书包和一件文化衫?
【23题答案】
【答案】(1)30元;(2)30名
【解析】
【详解】试题分析:(1)书包的价格=文化衫×2﹣6,据此列式即可求解.
(2)不等关系为:
350≤1800元﹣每人购买一个书包和一件文化衫的价钱≤400,列不等式组,求解取正整数值即可.
试题解析:解:(1)18×2﹣6=30(元),所以一个书包的价格是30元.
(2)设还能为x名学生每人购买一个书包和一件文化衫,根据题意得:
350≤1 800-(18+30)x≤400.
解得:.
∵x为正整数,∴x=30.
答:剩余经费还能为30名学生每人购买一个书包和一件文化衫.
点睛:解决本题关键是读懂题意,找到所求量的等量关系及符合题意的不等关系式组.
24.
某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.
(1)该校初三年级共有多少人参加春游?
(2)请你帮该校设计一种最省钱的租车方案.
【24题答案】
【答案】(1)288
(2)租42座车6辆和36座车1辆最省钱
【解析】
【分析】(1)设租36座的车辆,则租42座的客车辆.
不等关系:租42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人.
(2)根据(1)中求得的人数,进一步计算三种方案的费用:①只租36座客车;②只租42座客车;③合租两种车.再进一步比较得到结论即可.
【详解】解:(1)设租36座的车辆.
据题意得:,
解得:.
.
是整数,
.
则春游人数为:(人.
(2)方案①:租36座车8辆的费用:元;
方案②:租42座车7辆的费用:元;
方案③:,
座车越多越省钱,
又,余下人数正好36座,可以得出:租42座车6辆和36座车1辆的总费用:元.
,
方案③:租42座车6辆和36座车1辆最省钱.
【点睛】本题考查了不等关系,解题的关键是特别注意要能够分别求得每一种方案的价钱,再作比较。
