北师大版数学九年级下册 3.5确定圆的条件 课件 (共17张PPT)
文档属性
| 名称 | 北师大版数学九年级下册 3.5确定圆的条件 课件 (共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 284.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 07:21:19 | ||
图片预览





文档简介
(共18张PPT)
第三章 圆
3.5 确定圆的条件
知识点1:不在同一直线上的三个点确定一个圆
1.下列命题中不正确的是( )
A.过一点有无数个圆
B.过两点有无数个圆
C.过三个点可以作一个圆
D.直径是圆中最长的弦
C
2.(泸州测试)小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃片应该是( )
A.第①块
B.第②块
C.第③块
D.第④块
B
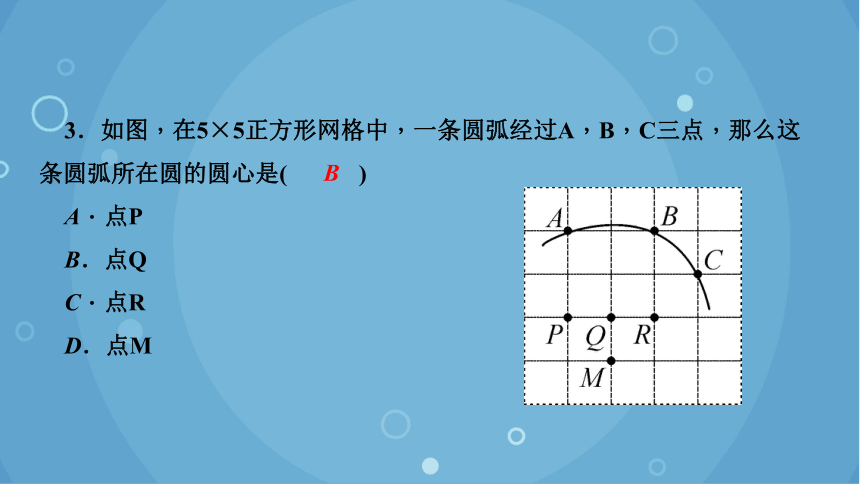
3.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P
B.点Q
C.点R
D.点M
B
4.如图所示,点A,B,C在直线l上,点D在l外,过这四点中的任意3个点,则能画圆的个数是______个.
3
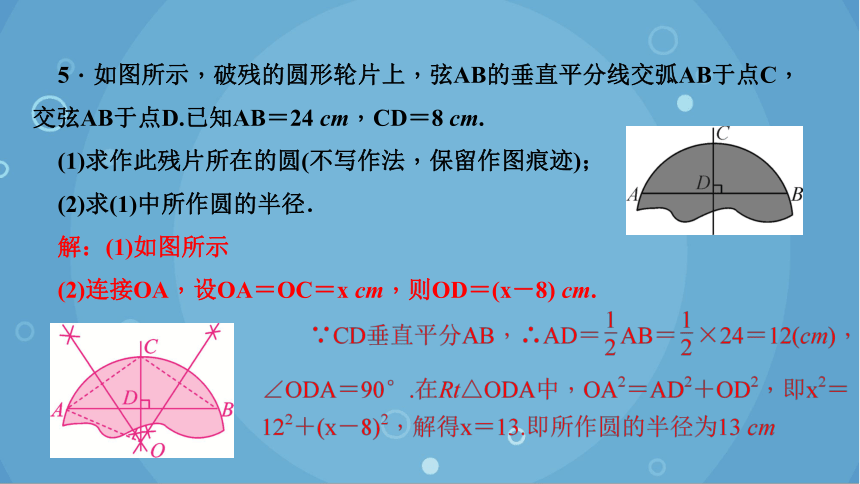
5.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知AB=24 cm,CD=8 cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
解:(1)如图所示
(2)连接OA,设OA=OC=x cm,则OD=(x-8) cm.
知识点2:三角形的外接圆
6.一个三角形的外心在其内部,则这个三角形是( )
A.任意三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
C
D
8.(扬州中考)如图,已知⊙O的半径为2,△ABC内接于⊙O,∠ACB=135°,则AB=_______________.
9.如图,网格的小正方形的边长均为1,小正方形的顶点叫做格点.△ABC的三个顶点都在格点上.
(1)在图上标出△ABC的外接圆的圆心O;
(2)△ABC的外接圆的面积是________.
解:(1)如图
(2)10π
A
11.(黄冈中考)如图,△ABC内接于⊙O,AB为⊙O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=6,则AC=_____________.
12.直角三角形的两边长分别为16和12,则此三角形外接圆的半径是______________.
10或8
14.在△ABC中,AB=AC=10,BC=12,求△ABC的外接圆半径.
16.(永州中考)如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.
1.判断平面内三点是否共圆的方法.
(1)确定三点是否共线,不共线则共圆;
(2)确定三条线段能否构成三角形,能够成三角形则共圆.
2.两种三角形的外接圆半径的求法.
(1)直角三角形的外心为斜边的中点,它的外接圆半径长为斜边的一半;
(2)等腰三角形的外接圆的半径,因其底边上的中线垂直于底边,故可借助于由半径、弦的一半,圆心到弦的垂线段所组成的直角三角形求解.
第三章 圆
3.5 确定圆的条件
知识点1:不在同一直线上的三个点确定一个圆
1.下列命题中不正确的是( )
A.过一点有无数个圆
B.过两点有无数个圆
C.过三个点可以作一个圆
D.直径是圆中最长的弦
C
2.(泸州测试)小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃片应该是( )
A.第①块
B.第②块
C.第③块
D.第④块
B
3.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P
B.点Q
C.点R
D.点M
B
4.如图所示,点A,B,C在直线l上,点D在l外,过这四点中的任意3个点,则能画圆的个数是______个.
3
5.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知AB=24 cm,CD=8 cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
解:(1)如图所示
(2)连接OA,设OA=OC=x cm,则OD=(x-8) cm.
知识点2:三角形的外接圆
6.一个三角形的外心在其内部,则这个三角形是( )
A.任意三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
C
D
8.(扬州中考)如图,已知⊙O的半径为2,△ABC内接于⊙O,∠ACB=135°,则AB=_______________.
9.如图,网格的小正方形的边长均为1,小正方形的顶点叫做格点.△ABC的三个顶点都在格点上.
(1)在图上标出△ABC的外接圆的圆心O;
(2)△ABC的外接圆的面积是________.
解:(1)如图
(2)10π
A
11.(黄冈中考)如图,△ABC内接于⊙O,AB为⊙O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=6,则AC=_____________.
12.直角三角形的两边长分别为16和12,则此三角形外接圆的半径是______________.
10或8
14.在△ABC中,AB=AC=10,BC=12,求△ABC的外接圆半径.
16.(永州中考)如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.
1.判断平面内三点是否共圆的方法.
(1)确定三点是否共线,不共线则共圆;
(2)确定三条线段能否构成三角形,能够成三角形则共圆.
2.两种三角形的外接圆半径的求法.
(1)直角三角形的外心为斜边的中点,它的外接圆半径长为斜边的一半;
(2)等腰三角形的外接圆的半径,因其底边上的中线垂直于底边,故可借助于由半径、弦的一半,圆心到弦的垂线段所组成的直角三角形求解.
