8.4 平行线的判定定理 课件(共28张PPT)
文档属性
| 名称 | 8.4 平行线的判定定理 课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-06 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
2022年春鲁教版数学
七年级下册数学精品课件
请找出图中的平行线!
它们为什么平行
情境引入
1.能根据“同位角相等,两直线平行”证明“内错角相等,两直线平行”,“同旁内角互补,两直线平行” 并能简单地应用这些结论.
2.初步了解证明的基本步骤和书写格式.
3.体会几何中推理的严谨性、书写的规范性,发展初步的演绎推理能力.
公理 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行
利用“同位角相等,两直线平行”这个基本事实,可以证明哪些判别两直线平行的真命题呢?
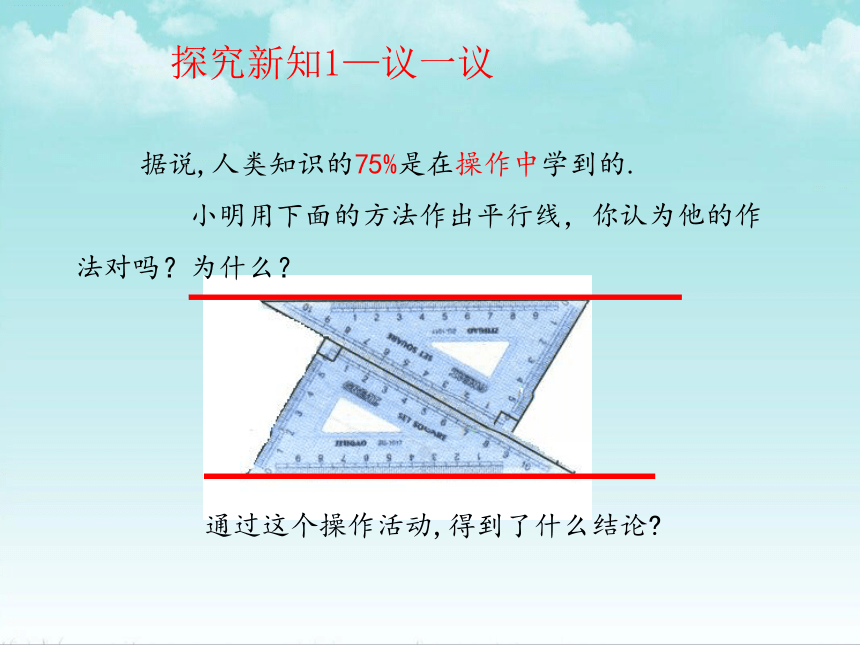
据说,人类知识的75%是在操作中学到的.
小明用下面的方法作出平行线,你认为他的作法对吗?为什么?
通过这个操作活动,得到了什么结论
探究新知1—议一议
定理 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
这个定理可以简单说成:内错角相等,两直线平行.
你能运用所学知识来证实它是一个真命题吗
探究新知1
已知:如图,∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2.求证:a∥b.
证明:∵∠1=∠2 (已知),
∠1=∠3(对顶角相等).
∴ ∠2=∠3(等量代换).
∴ a∥b(同位角相等,两直线平行).
你还有其他的方法解决本题吗?
a
b
c
1
3
2
你认为“两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行”这个命题正确吗?说明理由.
探究新知2
证明:∵ ∠1与∠2互补 (已知),
∴∠1+∠2=180°(互补的定义).
∴∠1= 180°-∠2(等式的性质).
又∵∠3+∠2=180° (平角的定义),
∴∠3= 180°-∠2(等式的性质).
∴∠1=∠3(等量代换).
∴ a∥b(同位角相等,两直线平行).
已知:如图,∠1和∠2是直线a、b被直线c截出的同旁内角,且∠1与∠2互补.求证:a∥b.
a
b
c
1
3
2
把你所悟到的证明一个真命题的方法,步骤,书写格式以及注意事项内化为一种方法.
证明一个命题的一般步骤:
(1)弄清条件和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
已给的公理,定义和定理以后都可以作为依据,用来证明新的命题.
证明的步骤
a
b
c
1
2
公理:
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理:
同旁内角互补,两直线平行.
∵∠1+∠2=180°, ∴ a∥b.
平行线的判定方法
a
b
c
2
1
a
b
c
1
2
例 已知:如图直线a, b被直线c所截,且∠1+∠2=180 °
求证: a∥b.
你有几种证明方法?
3
4
方法1:
∵ ∠ 1 + ∠ 2 = 180 °
∴ ∠ 2 = ∠ 4
∠ 1 + ∠ 4 = 180°
∴ a ∥b
5
证明:
新知应用
方法3:
∵ ∠ 1 + ∠ 2 = 180 °
∴ ∠ 2 = ∠ 5
∠ 1 + ∠ 5= 180 °
∴ a ∥b
方法2:
∵ ∠ 1 + ∠ 2 = 180°
∴ ∠ 2 + ∠ 3= 180 °
∠ 1 = ∠ 3
∴ a∥b
1.蜂房的底部由三个全等的四边形围成的,每个四边形的形状如图所示,其中∠α=109°28′, ∠β=70°32′.试确定这个四边形对边的位置关系,并证明你的结论.
A
B
C
D
目标检测1
解:AB∥CD,AD∥BC.
∵∠A+∠D=180°
∴ AB∥CD
∵∠A+∠B=180°
∴ AD∥BC
理由:
EF
内错角相等,两直线平行
BC
同旁内角互补,两直线平行
AD
BC
平行于同一条直线的两条直线互相平行
2.完成下列推理,并在括号中写出相应的根据.
∴ ∥ .
(1)如图甲所示
∵ ∠ADE= ∠DEF(已知)
∴ AD ∥ ( )
又∵ ∠EFC+ ∠C= 180 °
∴ EF ∥ ( )
( )
目标检测2
3.如果两条直线都和第三条直线垂直,那么这两条直线平行
已知,如图,直线a⊥c,b⊥c.
求证:a∥b.
证明:∵a⊥c,b⊥c(已知)
∴∠1=90°∠2=90°(垂直的定义)
∴∠1=∠2(等量代换)
∴b∥a(同位角相等,两直线平行)
目标检测3
4.已知:如图,CE平分∠ACD,∠1=∠B,
求证:AB∥CE
5.如图:∠1=53 ,∠2= 127 ,∠3= 53 ,
试说明直线AB与CD,BC与DE的位置关系.
证明: ∵ CE平分∠ACD,
∴∠1=∠2,
∵∠1=∠B, ∴∠ B =∠2,
∴AB∥CE
证明: ∵ ∠2= 127 ,
∴ ∠4=180 -127 =53 ,
∵ ∠3= 53
∴∠3=∠4,
∴AB∥CD.
∵∠1=∠3,
∴BC∥DE
目标检测4
( )
(2)如图乙所示
∵ AC ⊥ AB,BF ⊥ AB ( )
∴ ∠ CAB = ∠ ABF=90 ( )
∵ ∠ CAD= ∠ EBF=30 °( )
∴ = ( ) )
∴ ∥ .
等式的性质
垂直的性质
BE
∠EBA
内错角相等,两直线平行
∠BAD
AD
已知
已知
目标检测5
6.如图:直线AB,CD都和AE相交,∠1+∠A=180°
求证:AB//CD
C
B
A
D
2
1
E
∴∠1=∠2(等量代换)
∵∠1+∠A=180° ( )
∴∠2+∠A=180° (等量代换)
//
∴
( )
已知
AB CD
同旁内角互补,两直线平行
证明:∵∠1+∠3=180 (平角=180 )
∠2+∠3=180 (
平角=180 )
3
目标检测6
如图BE平分∠ABC,EC平分∠ BCD, ∠ E=90°
那么AB∥CD吗?为什么?
解:∵BE 平分∠ABC(已知)
∴∠___ =2∠1
∵EC平分∠BCD(已知)
∴∠____ =2∠2
∵∠E+∠1+∠2=180°
∴∠1+∠2=___°-∠E
∵∠E =90°(已知)
∴∠1+∠2=_ °
∴∠ABC +∠BCD =2∠_+2∠_=___°
∴_____ ( )
ABC
BCD
180
90
1 2 90
AB∥CD 同旁内角互补,两直线平行
拔尖自助餐
1.如图, ∠ D=∠EFC,那么( )
A.AD∥BC B.AB∥CD
C.EF∥BC D.AD∥EF
2.如图,判定AB∥CE的理由是( )
A.∠B=∠ACE B.∠A=∠ECD
C.∠B=∠ACB D.∠A=∠ACE
3.如图,下列推理正确的是( )
A.∵∠1=∠3,∴ a∥ b
B.∵∠1=∠2,∴a ∥b
C.∵∠1=∠2,∴c ∥ d
D.∵∠1=∠3,∴ c∥ d
当堂检测
D
D
B
同位角相等
两直线平行
同旁内角互补
两直线平行
内错角相等
两直线平行
∠1
∠2
∠1
∠2
∠1
∠2
小 结
1.平行线的判定方法:
(1)弄清条件和结论;
(2)根据题意画出相应的图形;
(3)根据条件和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
2.证明一个命题的一般步骤:
知识的升华
独立
作业
https://www.21cnjy.com/help/help_extract.php
2022年春鲁教版数学
七年级下册数学精品课件
请找出图中的平行线!
它们为什么平行
情境引入
1.能根据“同位角相等,两直线平行”证明“内错角相等,两直线平行”,“同旁内角互补,两直线平行” 并能简单地应用这些结论.
2.初步了解证明的基本步骤和书写格式.
3.体会几何中推理的严谨性、书写的规范性,发展初步的演绎推理能力.
公理 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行
利用“同位角相等,两直线平行”这个基本事实,可以证明哪些判别两直线平行的真命题呢?
据说,人类知识的75%是在操作中学到的.
小明用下面的方法作出平行线,你认为他的作法对吗?为什么?
通过这个操作活动,得到了什么结论
探究新知1—议一议
定理 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
这个定理可以简单说成:内错角相等,两直线平行.
你能运用所学知识来证实它是一个真命题吗
探究新知1
已知:如图,∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2.求证:a∥b.
证明:∵∠1=∠2 (已知),
∠1=∠3(对顶角相等).
∴ ∠2=∠3(等量代换).
∴ a∥b(同位角相等,两直线平行).
你还有其他的方法解决本题吗?
a
b
c
1
3
2
你认为“两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行”这个命题正确吗?说明理由.
探究新知2
证明:∵ ∠1与∠2互补 (已知),
∴∠1+∠2=180°(互补的定义).
∴∠1= 180°-∠2(等式的性质).
又∵∠3+∠2=180° (平角的定义),
∴∠3= 180°-∠2(等式的性质).
∴∠1=∠3(等量代换).
∴ a∥b(同位角相等,两直线平行).
已知:如图,∠1和∠2是直线a、b被直线c截出的同旁内角,且∠1与∠2互补.求证:a∥b.
a
b
c
1
3
2
把你所悟到的证明一个真命题的方法,步骤,书写格式以及注意事项内化为一种方法.
证明一个命题的一般步骤:
(1)弄清条件和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
已给的公理,定义和定理以后都可以作为依据,用来证明新的命题.
证明的步骤
a
b
c
1
2
公理:
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.
判定定理:
同旁内角互补,两直线平行.
∵∠1+∠2=180°, ∴ a∥b.
平行线的判定方法
a
b
c
2
1
a
b
c
1
2
例 已知:如图直线a, b被直线c所截,且∠1+∠2=180 °
求证: a∥b.
你有几种证明方法?
3
4
方法1:
∵ ∠ 1 + ∠ 2 = 180 °
∴ ∠ 2 = ∠ 4
∠ 1 + ∠ 4 = 180°
∴ a ∥b
5
证明:
新知应用
方法3:
∵ ∠ 1 + ∠ 2 = 180 °
∴ ∠ 2 = ∠ 5
∠ 1 + ∠ 5= 180 °
∴ a ∥b
方法2:
∵ ∠ 1 + ∠ 2 = 180°
∴ ∠ 2 + ∠ 3= 180 °
∠ 1 = ∠ 3
∴ a∥b
1.蜂房的底部由三个全等的四边形围成的,每个四边形的形状如图所示,其中∠α=109°28′, ∠β=70°32′.试确定这个四边形对边的位置关系,并证明你的结论.
A
B
C
D
目标检测1
解:AB∥CD,AD∥BC.
∵∠A+∠D=180°
∴ AB∥CD
∵∠A+∠B=180°
∴ AD∥BC
理由:
EF
内错角相等,两直线平行
BC
同旁内角互补,两直线平行
AD
BC
平行于同一条直线的两条直线互相平行
2.完成下列推理,并在括号中写出相应的根据.
∴ ∥ .
(1)如图甲所示
∵ ∠ADE= ∠DEF(已知)
∴ AD ∥ ( )
又∵ ∠EFC+ ∠C= 180 °
∴ EF ∥ ( )
( )
目标检测2
3.如果两条直线都和第三条直线垂直,那么这两条直线平行
已知,如图,直线a⊥c,b⊥c.
求证:a∥b.
证明:∵a⊥c,b⊥c(已知)
∴∠1=90°∠2=90°(垂直的定义)
∴∠1=∠2(等量代换)
∴b∥a(同位角相等,两直线平行)
目标检测3
4.已知:如图,CE平分∠ACD,∠1=∠B,
求证:AB∥CE
5.如图:∠1=53 ,∠2= 127 ,∠3= 53 ,
试说明直线AB与CD,BC与DE的位置关系.
证明: ∵ CE平分∠ACD,
∴∠1=∠2,
∵∠1=∠B, ∴∠ B =∠2,
∴AB∥CE
证明: ∵ ∠2= 127 ,
∴ ∠4=180 -127 =53 ,
∵ ∠3= 53
∴∠3=∠4,
∴AB∥CD.
∵∠1=∠3,
∴BC∥DE
目标检测4
( )
(2)如图乙所示
∵ AC ⊥ AB,BF ⊥ AB ( )
∴ ∠ CAB = ∠ ABF=90 ( )
∵ ∠ CAD= ∠ EBF=30 °( )
∴ = ( ) )
∴ ∥ .
等式的性质
垂直的性质
BE
∠EBA
内错角相等,两直线平行
∠BAD
AD
已知
已知
目标检测5
6.如图:直线AB,CD都和AE相交,∠1+∠A=180°
求证:AB//CD
C
B
A
D
2
1
E
∴∠1=∠2(等量代换)
∵∠1+∠A=180° ( )
∴∠2+∠A=180° (等量代换)
//
∴
( )
已知
AB CD
同旁内角互补,两直线平行
证明:∵∠1+∠3=180 (平角=180 )
∠2+∠3=180 (
平角=180 )
3
目标检测6
如图BE平分∠ABC,EC平分∠ BCD, ∠ E=90°
那么AB∥CD吗?为什么?
解:∵BE 平分∠ABC(已知)
∴∠___ =2∠1
∵EC平分∠BCD(已知)
∴∠____ =2∠2
∵∠E+∠1+∠2=180°
∴∠1+∠2=___°-∠E
∵∠E =90°(已知)
∴∠1+∠2=_ °
∴∠ABC +∠BCD =2∠_+2∠_=___°
∴_____ ( )
ABC
BCD
180
90
1 2 90
AB∥CD 同旁内角互补,两直线平行
拔尖自助餐
1.如图, ∠ D=∠EFC,那么( )
A.AD∥BC B.AB∥CD
C.EF∥BC D.AD∥EF
2.如图,判定AB∥CE的理由是( )
A.∠B=∠ACE B.∠A=∠ECD
C.∠B=∠ACB D.∠A=∠ACE
3.如图,下列推理正确的是( )
A.∵∠1=∠3,∴ a∥ b
B.∵∠1=∠2,∴a ∥b
C.∵∠1=∠2,∴c ∥ d
D.∵∠1=∠3,∴ c∥ d
当堂检测
D
D
B
同位角相等
两直线平行
同旁内角互补
两直线平行
内错角相等
两直线平行
∠1
∠2
∠1
∠2
∠1
∠2
小 结
1.平行线的判定方法:
(1)弄清条件和结论;
(2)根据题意画出相应的图形;
(3)根据条件和结论写出已知,求证;
(4)分析证明思路,写出证明过程.
2.证明一个命题的一般步骤:
知识的升华
独立
作业
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
