8.5 平行线的性质定理 课件(共23张PPT)
文档属性
| 名称 | 8.5 平行线的性质定理 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-06 21:17:02 | ||
图片预览






文档简介
(共23张PPT)
2022年春鲁教版数学
七年级下册数学精品课件
8.5 平行线的性质定理
判定方法1 同位角相等,两直线平行.
判定方法2 内错角相等,两直线平行.
判定方法3 同旁内角互补,两直线平行.
1.梳理旧知,引出新课
结论
平行线的判定
条件
两条平行线
被第三条直
线所截
1.梳理旧知,引出新课
条件
结论
同位角相等
内错角相等
同旁内角互补
证明:两条平行直线被第三条直线所截,同位角相等.
(1)你能作出相关的图形吗?
(2)你能根据所作的图形写出已知、求证吗?
(3)你能说说证明的思路吗?
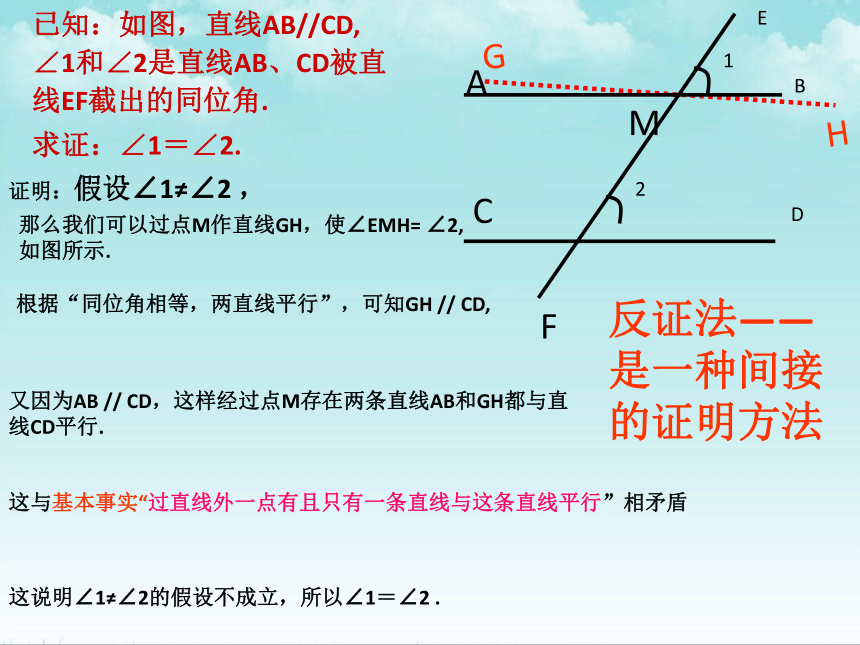
已知:如图,直线AB//CD, ∠1和∠2是直线AB,CD被直线EF截出的同位角.
求证:∠1=∠2.
B
D
E
2
1
A
C
F
M
G
H
反证法——是一种间接的证明方法
又因为AB // CD,这样经过点M存在两条直线AB和GH都与直线CD平行.
证明:假设∠1≠∠2 ,
这说明∠1≠∠2的假设不成立,所以∠1=∠2 .
这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾
根据“同位角相等,两直线平行”,可知GH // CD,
已知:如图,直线AB//CD, ∠1和∠2是直线AB、CD被直线EF截出的同位角.
求证:∠1=∠2.
B
D
E
2
1
A
C
F
M
那么我们可以过点M作直线GH,使∠EMH= ∠2,如图所示.
定理1:两条平行直线被第三条直线 所截,同位角相等.
(简述为:两直线平行,同位角相等.)
证明:两条平行直线被第三条直线所截,内错角相等.
1
a
b
c
2
3
已知:如图, 直线a//b, ∠1和∠2是直线a、b被直线c截出的内错角.
求证:∠1=∠2.
(1)你能作出相关的图形吗?
(2)你能根据所作的图形写出已知、求证吗?
(3)你能说说证明的思路吗?
已知:如图,直线a∥b, ∠1和∠2
是直线a、b被直线 c截出的内错角 .
求证:∠1=∠2.
1
2
3
a
b
c
证明:∵a∥b ( )
∴∠3=∠2
( )
又∵ ∠3=∠1 ( )
∴∠1=∠2 ( )
已知
两直线平行,同位角相等
对顶角相等
等量代换
定理2:两条平行直线被第三条直线 所截,内错角相等.
(简述为:两直线平行,内错角相等.)
已知:如图,直线a//b,∠1和∠2是直线a,b被直线c截出的同旁内角.
求证:∠1+∠2=180°.
证明:两条平行直线被第三条直线所截, 同旁内角互补.
a
b
c
1
2
3
3
已知:如图,直线a//b,∠1和∠2是直线a,b被直线c截出的同旁内角.
求证:∠1+∠2=180°
a
b
c
1
2
3
证法1: a//b(已知)
∠3=∠2(两直线平行,同位角相等)
又 ∠1+∠3=180°(平角定义)
∠1+∠2=180°(等量代换)
已知:如图,直线a//b,∠1和∠2是直线a,b被直线c截出的同旁内角.
求证:∠1+∠2=180°.
a
b
c
1
2
3
证法2: a//b (已知)
∠3=∠2 (两直线平行,内错角相等)
又 ∠1+∠3=180°(补角定义)
∠1+∠2=180°(等量代换)
定理3:两条平行直线被第三条直线 所截,同旁内角互补.
(简述为:两直线平行,同旁内角互补.)
定理:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
(简述为:平行于同一条直线的两条直线平行)
例1 已知:如图, ∠1,∠2, ∠3是直线 a, b, c被直线d截出的同位角,且b∥ a, c∥a.
求证:b∥c.
a
b
c
d
2
1
3
练一练
1.已知平行线AB,CD被直线AE所截
A
E
D
C
B
1
2
3
4
(1)若从∠1=110°,可以知道
∠2是多少度,为什么?
(2)若∠1=110°,可以知道
∠3是多少度,为什么?
(3)若∠1=110°,可以知道
∠4是多少度,为什么?
2.一自行车运动员在一条公路上骑车,两次拐弯后,和原来的方向相同(即拐弯前后的两条路互相平行),若测得第一次拐弯的∠B是142°,则第二次拐弯的∠C应是多少度才合理?为什么?
B
C
A
D
答:∠C=142°.
因为两直线平行,内错角相等
3.如图,由AB//CD,可以得到( )
A.∠1=∠2
B.∠2=∠3
C.∠1=∠4
D.∠3=∠4
B
D
A
C
1
2
3
4
C
练 一 练
4.如图,AB ∥ CD, ∠ 1=145°, ∠2= 130°,求∠ HEC的度数.
E
A
B
C
D
1
2
F
H
3
4
证明:过点E作直线EF ∥ AB ∵ AB ∥ CD( )
∴ EF ∥ CD( )
两直线平行
判定
性质
已知
得到
得到
已知
(1)平行线的性质是什么?
小结与回顾:
(2)说说平行线的“判定”与“性质”有什么不同
同位角相等
内错角相等
同旁内角互补
今天的收获
1.平行的的判定与性质:
2.证明的一般步骤
两直线平行 →
←
性质
判定
同位角相等
内错角相等
同旁内角互补
https://www.21cnjy.com/help/help_extract.php
2022年春鲁教版数学
七年级下册数学精品课件
8.5 平行线的性质定理
判定方法1 同位角相等,两直线平行.
判定方法2 内错角相等,两直线平行.
判定方法3 同旁内角互补,两直线平行.
1.梳理旧知,引出新课
结论
平行线的判定
条件
两条平行线
被第三条直
线所截
1.梳理旧知,引出新课
条件
结论
同位角相等
内错角相等
同旁内角互补
证明:两条平行直线被第三条直线所截,同位角相等.
(1)你能作出相关的图形吗?
(2)你能根据所作的图形写出已知、求证吗?
(3)你能说说证明的思路吗?
已知:如图,直线AB//CD, ∠1和∠2是直线AB,CD被直线EF截出的同位角.
求证:∠1=∠2.
B
D
E
2
1
A
C
F
M
G
H
反证法——是一种间接的证明方法
又因为AB // CD,这样经过点M存在两条直线AB和GH都与直线CD平行.
证明:假设∠1≠∠2 ,
这说明∠1≠∠2的假设不成立,所以∠1=∠2 .
这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾
根据“同位角相等,两直线平行”,可知GH // CD,
已知:如图,直线AB//CD, ∠1和∠2是直线AB、CD被直线EF截出的同位角.
求证:∠1=∠2.
B
D
E
2
1
A
C
F
M
那么我们可以过点M作直线GH,使∠EMH= ∠2,如图所示.
定理1:两条平行直线被第三条直线 所截,同位角相等.
(简述为:两直线平行,同位角相等.)
证明:两条平行直线被第三条直线所截,内错角相等.
1
a
b
c
2
3
已知:如图, 直线a//b, ∠1和∠2是直线a、b被直线c截出的内错角.
求证:∠1=∠2.
(1)你能作出相关的图形吗?
(2)你能根据所作的图形写出已知、求证吗?
(3)你能说说证明的思路吗?
已知:如图,直线a∥b, ∠1和∠2
是直线a、b被直线 c截出的内错角 .
求证:∠1=∠2.
1
2
3
a
b
c
证明:∵a∥b ( )
∴∠3=∠2
( )
又∵ ∠3=∠1 ( )
∴∠1=∠2 ( )
已知
两直线平行,同位角相等
对顶角相等
等量代换
定理2:两条平行直线被第三条直线 所截,内错角相等.
(简述为:两直线平行,内错角相等.)
已知:如图,直线a//b,∠1和∠2是直线a,b被直线c截出的同旁内角.
求证:∠1+∠2=180°.
证明:两条平行直线被第三条直线所截, 同旁内角互补.
a
b
c
1
2
3
3
已知:如图,直线a//b,∠1和∠2是直线a,b被直线c截出的同旁内角.
求证:∠1+∠2=180°
a
b
c
1
2
3
证法1: a//b(已知)
∠3=∠2(两直线平行,同位角相等)
又 ∠1+∠3=180°(平角定义)
∠1+∠2=180°(等量代换)
已知:如图,直线a//b,∠1和∠2是直线a,b被直线c截出的同旁内角.
求证:∠1+∠2=180°.
a
b
c
1
2
3
证法2: a//b (已知)
∠3=∠2 (两直线平行,内错角相等)
又 ∠1+∠3=180°(补角定义)
∠1+∠2=180°(等量代换)
定理3:两条平行直线被第三条直线 所截,同旁内角互补.
(简述为:两直线平行,同旁内角互补.)
定理:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
(简述为:平行于同一条直线的两条直线平行)
例1 已知:如图, ∠1,∠2, ∠3是直线 a, b, c被直线d截出的同位角,且b∥ a, c∥a.
求证:b∥c.
a
b
c
d
2
1
3
练一练
1.已知平行线AB,CD被直线AE所截
A
E
D
C
B
1
2
3
4
(1)若从∠1=110°,可以知道
∠2是多少度,为什么?
(2)若∠1=110°,可以知道
∠3是多少度,为什么?
(3)若∠1=110°,可以知道
∠4是多少度,为什么?
2.一自行车运动员在一条公路上骑车,两次拐弯后,和原来的方向相同(即拐弯前后的两条路互相平行),若测得第一次拐弯的∠B是142°,则第二次拐弯的∠C应是多少度才合理?为什么?
B
C
A
D
答:∠C=142°.
因为两直线平行,内错角相等
3.如图,由AB//CD,可以得到( )
A.∠1=∠2
B.∠2=∠3
C.∠1=∠4
D.∠3=∠4
B
D
A
C
1
2
3
4
C
练 一 练
4.如图,AB ∥ CD, ∠ 1=145°, ∠2= 130°,求∠ HEC的度数.
E
A
B
C
D
1
2
F
H
3
4
证明:过点E作直线EF ∥ AB ∵ AB ∥ CD( )
∴ EF ∥ CD( )
两直线平行
判定
性质
已知
得到
得到
已知
(1)平行线的性质是什么?
小结与回顾:
(2)说说平行线的“判定”与“性质”有什么不同
同位角相等
内错角相等
同旁内角互补
今天的收获
1.平行的的判定与性质:
2.证明的一般步骤
两直线平行 →
←
性质
判定
同位角相等
内错角相等
同旁内角互补
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
