人教版数学七年级下册 5.3.1 平行线的性质 课件(共33张PPT)
文档属性
| 名称 | 人教版数学七年级下册 5.3.1 平行线的性质 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 485.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 08:19:22 | ||
图片预览







文档简介
(共33张PPT)
5.3.1 平行线的性质
第五章 相交线与平行线
1.掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.
2.能够根据平行线的性质进行简单的推理.
3.区分平行线的性质和判定的关系,培养学生逆向思维的能力.
重点难点:
1.分清平行线的性质和判定;已知平行用性质,要证平行用判定.
2.能够综合运用平行线性质和判定进行推理证明.
学习目标:
情景导入
利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行.反过来,如果两条直线平行,同位角、内错角、同旁内角又各有什么关系呢?这就是我们下面要学行线的性质.
类似于研究平行线的判定,我们先来研究两条直线平行时,它们被第三条直线截得的同位角的关系.
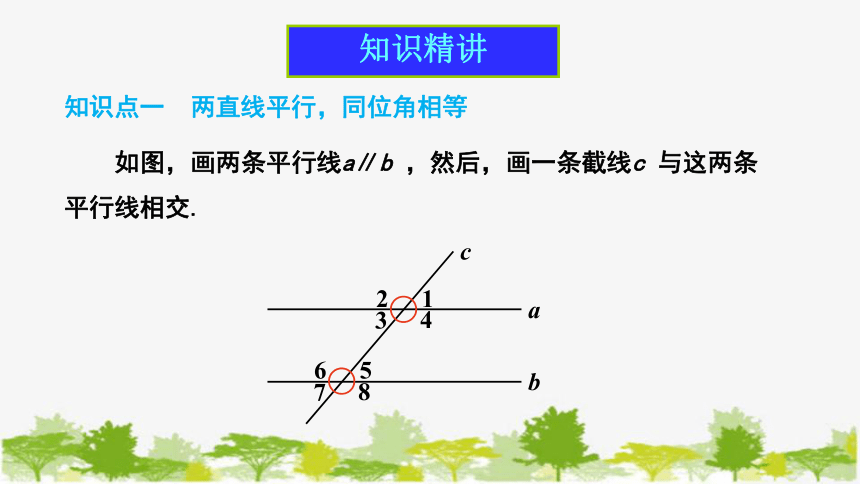
如图,画两条平行线a∥b ,然后,画一条截线c 与这两条平行线相交.
a
b
c
1
3
2
4
5
7
6
8
知识点一 两直线平行,同位角相等
知识精讲
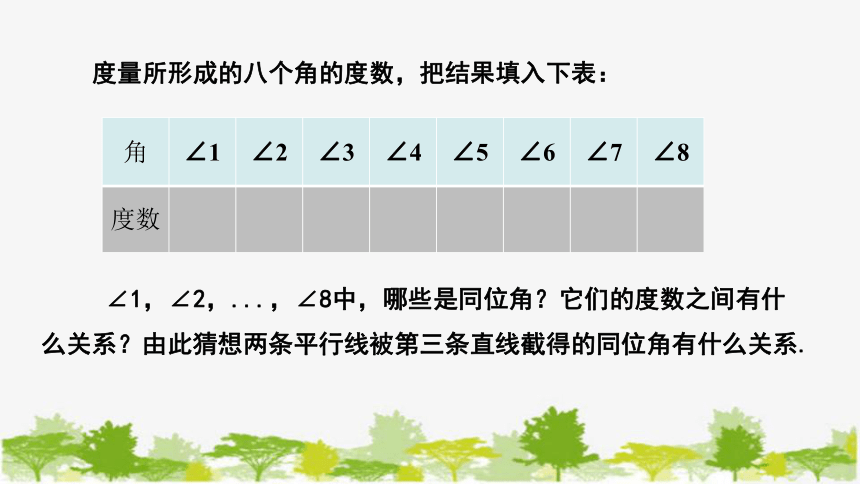
度量所形成的八个角的度数,把结果填入下表:
∠1,∠2,...,∠8中,哪些是同位角?它们的度数之间有什么关系?由此猜想两条平行线被第三条直线截得的同位角有什么关系.
角 ∠1 ∠2 ∠3 ∠4 ∠5 ∠6 ∠7 ∠8
度数
一般地,平行线具有性质:
性质1 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
几何语言:
∵a∥b(已知)
∴∠1=∠2
(两直线平行,同位角相等)
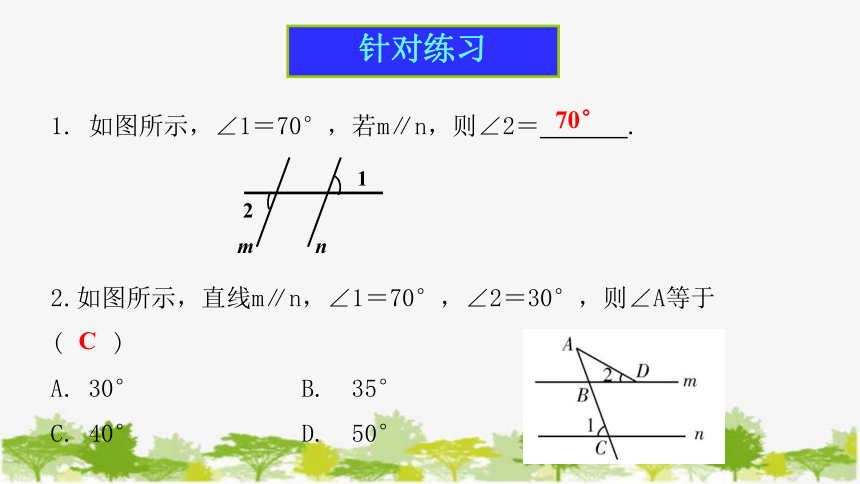
针对练习
1. 如图所示,∠1=70°,若m∥n,则∠2= .
2.如图所示,直线m∥n,∠1=70°,∠2=30°,则∠A等于 ( )
A. 30° B. 35°
C. 40° D. 50°
70°
C
n
m
2
1
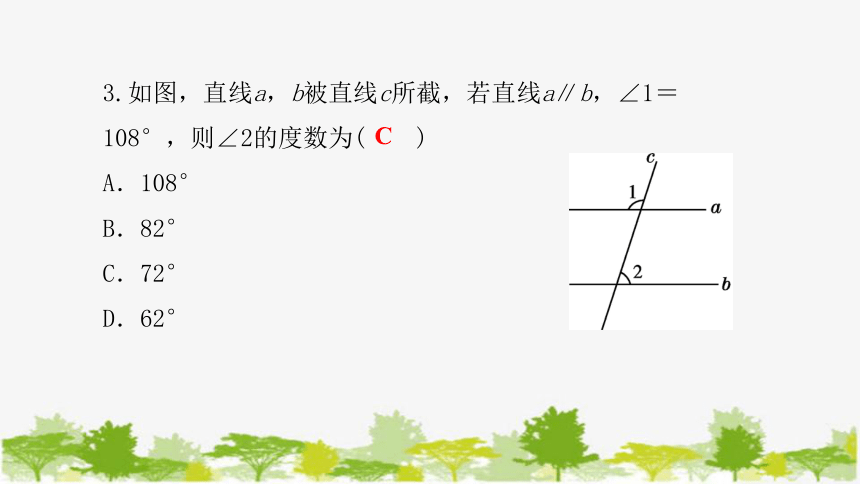
3.如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( )
A.108°
B.82°
C.72°
D.62°
C
在上一节中,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行线”,类似地,已知两直线平行,同位角相等,能否得到内错角之间的数量关系?
知识点二 两直线平行,内错角相等
如图,已知a∥b,那么 2与 3相等吗?为什么
b
1
2
a
c
3
解:∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
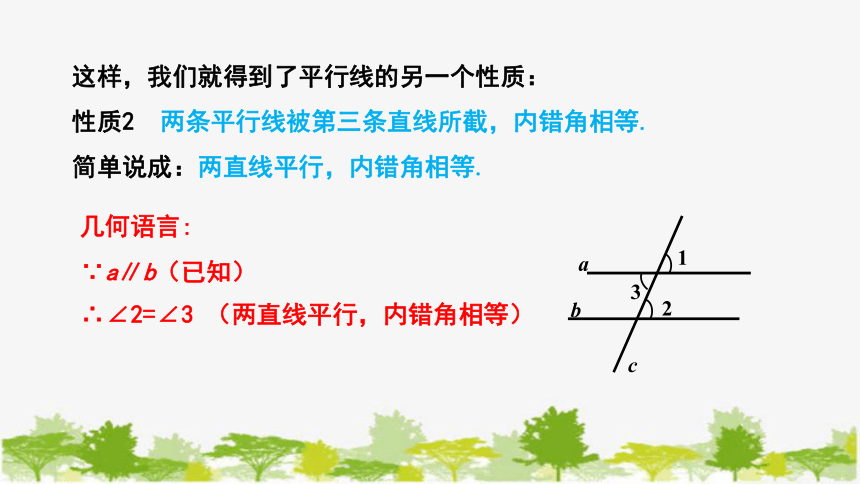
这样,我们就得到了平行线的另一个性质:
性质2 两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
b
1
2
a
c
3
几何语言:
∵a∥b(已知)
∴∠2=∠3 (两直线平行,内错角相等)
知识点三 两直线平行,同旁内角相等
如图,已知a∥b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
解: ∵a∥b (已知),
∴ 1= 2(两直线平行,同位角相等).
∵ 1+ 4=180°(邻补角的性质),
∴ 2+ 4=180°(等量代换).
类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
这样,我们就得到了平行线的另一个性质:
性质3 两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
几何语言:
∵a∥b(已知)
∴∠2+∠4=180°
(两直线平行,同旁内角互补)
b
1
2
a
c
4
1.如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )
A.120°
B.100°
C.80°
D.60°
D
针对练习
知识点四 平行线性质和判定的综合应用
证明:∵ AD ∥BC(已知)
∴ ∠A+∠B=180°
( )
∵ ∠AEF=∠B(已知)
∴ ∠A+∠AEF=180°(等量代换)
∴ AD∥EF( )
两直线平行,同旁内角互补
同旁内角互补,两直线平行
如图,已知:AD ∥ BC, ∠AEF = ∠B,求证:AD ∥EF.
复习回顾
两直线平行
1、同位角相等
2、内错角相等
3、同旁内角互补
平行线的判定方法:
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
根据右图,填空:
①如果∠1=∠C,
那么__∥_( )
② 如果∠1=∠B
那么__∥_( )
③ 如果∠2+∠B=180°,
那么__∥__( )
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
角的关系
线的关系
思考:
条件和结论反过来,成立吗?
条件是____、 结论是____?(角/线的关系)
判定
由“角”定“线”
条件: a∥b,探索同位角的关系
1.画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 任选一组同位角、内错角或同旁内角,度量这些角,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
a
b
c
1
3
2
4
8
5
7
6
发现: ________________________
同位角相等
探究一
1. 任意一条直线去截平行线a、b所得的同位角都相等( )
2. 任意一条直线去截两条不平行的直线a、b所得的同位角都相等( )
发现性质:
两条_____线被第三条直线所截,同位角_______.
平行
相等
思考判断
平行线的性质1:
结论
两条_____线被第三条直线所截,同位角_______.
∴∠1=∠2.
∵a∥b,
简写为:_______________________
符号语言:
b
1
2
a
平行
相等
两直线平行,同位角相等.
判定:任意两条线被第三条直线所截,同位角都相等吗?( )
猜想:两直线平行,内错角_____,同旁内角_____
相等
互补
性质发现
如图:已知a//b,那么 2与 3相等吗?
利用平行线的性质1,说明理由
解∵a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
探究二
b
1
2
a
c
3
平行线的性质2:
结论
两条_____线被第三条直线所截,内错角_______.
∴∠2=∠3.
∵a∥b,
简写为:_______________________
符号语言:
平行
相等
两直线平行,内错角相等.
判定:任意两条线被第三条直线所截,内错角都相等吗?( )
b
1
2
a
c
3
性质发现
解: ∵a//b (已知),
如图,已知a//b,那么 2与 4有什么关系呢?利用平行线的性质1 ,说明理由
b
1
2
a
c
4
∴ 1= 2(两直线平行,
同位角相等).
∵ 1+ 4=180°
(邻补角定义),
∴ 2+ 4=180°
(等量代换).
探究三
平行线的性质3:
结论
两条_____线被第三条直线所截,同旁内角_______.
∴ 2+ 4=180°
∵a∥b,
简写为:_______________________
符号语言:
平行
互补
两直线平行,同旁内角互补.
b
1
2
a
c
4
性质发现
快速口答:当a∥b时 ,∠1 与∠2有什么关系 依据?
a
b
1
2
a
b
1
2
b
a
1
2
(1) (2) (3)
(1) 1+ 2=180°
两直线平行,同旁内角互补.
(2) 1= 2
两直线平行,内错角相等.
(3) 1= 2
两直线平行,同位角相等.
平行线的性质:
由______,定_____
线
角
a
b
c
1
2
3
4
50°
两直线平行,同位角相等.
50°
两直线平行,内错角相等.
130°
两直线平行,同旁内角互补.
变式1:已知∠3 =∠4,∠1=47°,求∠2的度数?
∴∠ 2= 47( )
解:∵ ∠3 =∠4( )
∴a∥b( )
又∵∠ 1 = 470 ( )
c
1
2
3
4
a
b
d
两直线平行,同位角相等
同位角相等,两直线平行
已知
已知
A
B
C
D
115°
100°
变式2:如图,是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=100°。已知梯形的两底AD//BC,请你求出另外两个角的度数。
解:∵AD∥BC
∴∠A和∠B互补(两直线平行,同旁内角互补)
∠D和∠C互补(两直线平行,同旁内角互补)又∵∠A=115°,∠D=100°
∴∠B=180°-∠A=180°-115°=65°
∠C=180°-∠D=180°-100°=80°
即梯形另外两个角的度数是:65°,80°。
5.如图在四边形ABCD中,已知AB∥CD,
∠B = 600.
①求∠C的度数;
②由已知条件能否求得∠A的度数
A
B
C
D
解: ① ∵ AB∥CD(已知),
∴ ∠B + ∠C= 1800(两直线平行,同旁内角互补).
∴∠C = 1800 -∠B =1200
②根据题目的已知条件,
无法求出∠A的度数.
施展你的才能
B
变式
两直线平行
同位角相等
内错角相等
同旁内角互补
2.线的关系
角的关系
判定
性质
平行线的性质和平行线的判定方法的 区 别 与 联 系
小结
1.平行线的性质
平行线的性质:
由“____”定“____”
由“____”定“____”
3.平行线的判定:
线
角
角
线
( )
( )
5.3.1 平行线的性质
第五章 相交线与平行线
1.掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.
2.能够根据平行线的性质进行简单的推理.
3.区分平行线的性质和判定的关系,培养学生逆向思维的能力.
重点难点:
1.分清平行线的性质和判定;已知平行用性质,要证平行用判定.
2.能够综合运用平行线性质和判定进行推理证明.
学习目标:
情景导入
利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行.反过来,如果两条直线平行,同位角、内错角、同旁内角又各有什么关系呢?这就是我们下面要学行线的性质.
类似于研究平行线的判定,我们先来研究两条直线平行时,它们被第三条直线截得的同位角的关系.
如图,画两条平行线a∥b ,然后,画一条截线c 与这两条平行线相交.
a
b
c
1
3
2
4
5
7
6
8
知识点一 两直线平行,同位角相等
知识精讲
度量所形成的八个角的度数,把结果填入下表:
∠1,∠2,...,∠8中,哪些是同位角?它们的度数之间有什么关系?由此猜想两条平行线被第三条直线截得的同位角有什么关系.
角 ∠1 ∠2 ∠3 ∠4 ∠5 ∠6 ∠7 ∠8
度数
一般地,平行线具有性质:
性质1 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
几何语言:
∵a∥b(已知)
∴∠1=∠2
(两直线平行,同位角相等)
针对练习
1. 如图所示,∠1=70°,若m∥n,则∠2= .
2.如图所示,直线m∥n,∠1=70°,∠2=30°,则∠A等于 ( )
A. 30° B. 35°
C. 40° D. 50°
70°
C
n
m
2
1
3.如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( )
A.108°
B.82°
C.72°
D.62°
C
在上一节中,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行线”,类似地,已知两直线平行,同位角相等,能否得到内错角之间的数量关系?
知识点二 两直线平行,内错角相等
如图,已知a∥b,那么 2与 3相等吗?为什么
b
1
2
a
c
3
解:∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
这样,我们就得到了平行线的另一个性质:
性质2 两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
b
1
2
a
c
3
几何语言:
∵a∥b(已知)
∴∠2=∠3 (两直线平行,内错角相等)
知识点三 两直线平行,同旁内角相等
如图,已知a∥b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
解: ∵a∥b (已知),
∴ 1= 2(两直线平行,同位角相等).
∵ 1+ 4=180°(邻补角的性质),
∴ 2+ 4=180°(等量代换).
类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
这样,我们就得到了平行线的另一个性质:
性质3 两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
几何语言:
∵a∥b(已知)
∴∠2+∠4=180°
(两直线平行,同旁内角互补)
b
1
2
a
c
4
1.如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )
A.120°
B.100°
C.80°
D.60°
D
针对练习
知识点四 平行线性质和判定的综合应用
证明:∵ AD ∥BC(已知)
∴ ∠A+∠B=180°
( )
∵ ∠AEF=∠B(已知)
∴ ∠A+∠AEF=180°(等量代换)
∴ AD∥EF( )
两直线平行,同旁内角互补
同旁内角互补,两直线平行
如图,已知:AD ∥ BC, ∠AEF = ∠B,求证:AD ∥EF.
复习回顾
两直线平行
1、同位角相等
2、内错角相等
3、同旁内角互补
平行线的判定方法:
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
根据右图,填空:
①如果∠1=∠C,
那么__∥_( )
② 如果∠1=∠B
那么__∥_( )
③ 如果∠2+∠B=180°,
那么__∥__( )
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
角的关系
线的关系
思考:
条件和结论反过来,成立吗?
条件是____、 结论是____?(角/线的关系)
判定
由“角”定“线”
条件: a∥b,探索同位角的关系
1.画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 任选一组同位角、内错角或同旁内角,度量这些角,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
a
b
c
1
3
2
4
8
5
7
6
发现: ________________________
同位角相等
探究一
1. 任意一条直线去截平行线a、b所得的同位角都相等( )
2. 任意一条直线去截两条不平行的直线a、b所得的同位角都相等( )
发现性质:
两条_____线被第三条直线所截,同位角_______.
平行
相等
思考判断
平行线的性质1:
结论
两条_____线被第三条直线所截,同位角_______.
∴∠1=∠2.
∵a∥b,
简写为:_______________________
符号语言:
b
1
2
a
平行
相等
两直线平行,同位角相等.
判定:任意两条线被第三条直线所截,同位角都相等吗?( )
猜想:两直线平行,内错角_____,同旁内角_____
相等
互补
性质发现
如图:已知a//b,那么 2与 3相等吗?
利用平行线的性质1,说明理由
解∵a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
探究二
b
1
2
a
c
3
平行线的性质2:
结论
两条_____线被第三条直线所截,内错角_______.
∴∠2=∠3.
∵a∥b,
简写为:_______________________
符号语言:
平行
相等
两直线平行,内错角相等.
判定:任意两条线被第三条直线所截,内错角都相等吗?( )
b
1
2
a
c
3
性质发现
解: ∵a//b (已知),
如图,已知a//b,那么 2与 4有什么关系呢?利用平行线的性质1 ,说明理由
b
1
2
a
c
4
∴ 1= 2(两直线平行,
同位角相等).
∵ 1+ 4=180°
(邻补角定义),
∴ 2+ 4=180°
(等量代换).
探究三
平行线的性质3:
结论
两条_____线被第三条直线所截,同旁内角_______.
∴ 2+ 4=180°
∵a∥b,
简写为:_______________________
符号语言:
平行
互补
两直线平行,同旁内角互补.
b
1
2
a
c
4
性质发现
快速口答:当a∥b时 ,∠1 与∠2有什么关系 依据?
a
b
1
2
a
b
1
2
b
a
1
2
(1) (2) (3)
(1) 1+ 2=180°
两直线平行,同旁内角互补.
(2) 1= 2
两直线平行,内错角相等.
(3) 1= 2
两直线平行,同位角相等.
平行线的性质:
由______,定_____
线
角
a
b
c
1
2
3
4
50°
两直线平行,同位角相等.
50°
两直线平行,内错角相等.
130°
两直线平行,同旁内角互补.
变式1:已知∠3 =∠4,∠1=47°,求∠2的度数?
∴∠ 2= 47( )
解:∵ ∠3 =∠4( )
∴a∥b( )
又∵∠ 1 = 470 ( )
c
1
2
3
4
a
b
d
两直线平行,同位角相等
同位角相等,两直线平行
已知
已知
A
B
C
D
115°
100°
变式2:如图,是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=100°。已知梯形的两底AD//BC,请你求出另外两个角的度数。
解:∵AD∥BC
∴∠A和∠B互补(两直线平行,同旁内角互补)
∠D和∠C互补(两直线平行,同旁内角互补)又∵∠A=115°,∠D=100°
∴∠B=180°-∠A=180°-115°=65°
∠C=180°-∠D=180°-100°=80°
即梯形另外两个角的度数是:65°,80°。
5.如图在四边形ABCD中,已知AB∥CD,
∠B = 600.
①求∠C的度数;
②由已知条件能否求得∠A的度数
A
B
C
D
解: ① ∵ AB∥CD(已知),
∴ ∠B + ∠C= 1800(两直线平行,同旁内角互补).
∴∠C = 1800 -∠B =1200
②根据题目的已知条件,
无法求出∠A的度数.
施展你的才能
B
变式
两直线平行
同位角相等
内错角相等
同旁内角互补
2.线的关系
角的关系
判定
性质
平行线的性质和平行线的判定方法的 区 别 与 联 系
小结
1.平行线的性质
平行线的性质:
由“____”定“____”
由“____”定“____”
3.平行线的判定:
线
角
角
线
( )
( )
