沪科版物理八年级同步提优训练:9.2 阿基米德原理 (共2课时 有解析)
文档属性
| 名称 | 沪科版物理八年级同步提优训练:9.2 阿基米德原理 (共2课时 有解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 335.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-06 17:25:07 | ||
图片预览




文档简介
第二节 阿基米德原理
第1课时 阿基米德原理的简单应用
1 影响浮力大小的因素
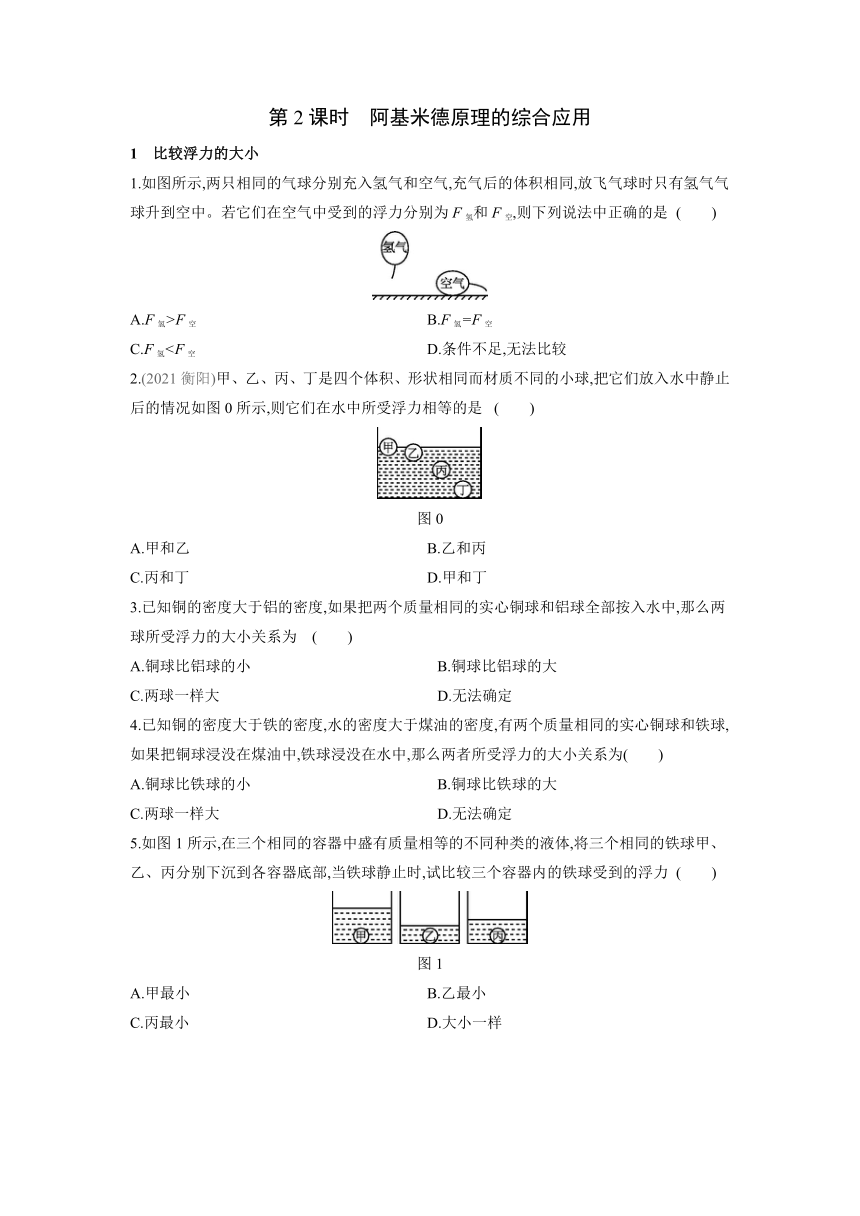
1.如图所示,把挂在弹簧测力计下的金属圆柱体缓慢浸入水中(水足够深),在圆柱体接触容器底之前,图中能正确反映弹簧测力计示数F和圆柱体下降高度h关系的图像是
( )
2.在“探究浮力的大小跟哪些因素有关”的实验中,小明提出如下猜想:
猜想1:浮力的大小可能与液体密度有关;
猜想2:浮力的大小可能与物体重力有关;
猜想3:浮力的大小可能与物体形状有关;
猜想4:浮力的大小可能与排开液体的体积有关。
(1)如图所示,用手把饮料罐按入水中,饮料罐浸入水中越深,手会感到越吃力。这个事实可以支持以上猜想 (填数字)。
(2)为了研究猜想1和猜想2,小明使用体积相同的A、B、C三个圆柱体,测得重力分别为4 N、4.5 N和5 N,然后进行如图所示的实验。
①在序号a的实验中,物体所受的浮力为 N。
②比较 、 、e三次实验,可得出初步结论:浮力大小与液体密度有关。
③进一步分析可知,在其他条件相同时,液体的密度越大,物体所受的浮力越 (选填“大”或“小”)。
④比较a、b、c三次实验,可得出结论:浮力的大小与物体的重力 (选填“有”或“无”)关。
(3)为了研究猜想3,小明用两块相同的橡皮泥分别捏成圆锥体和圆柱体进行如图所示的实验,由此小明得出结论:浮力的大小与物体的形状有关。小珍认为该结论不可靠,主要原因是
。
2 阿基米德原理
3.将一个重为10 N的物体放入一装满水的溢水杯中,从杯中溢出3 N的水,则物体在水中受到的浮力大小为 ( )
A.10 N B.3 N
C.13 N D.7 N
4.将一个重为1 N的物体放入一盛有水但不满的烧杯中,从杯中溢出了0.6 N的水,则物体受到的浮力 ( )
A.等于1 N B.等于0.6 N
C.一定大于0.6 N D.无法确定
5.(2020黔南州)如图所示,重为5 N、体积为0.2×10-3 m3的物体用细线系在弹簧测力计的挂钩上,将它浸没在水中,物体受到的浮力是 N, 静止时弹簧测力计的示数是 N。(g取10 N/kg)
6.(2021益阳)在弹簧测力计下端悬挂一个金属零件,测力计的示数是5 N。当把零件浸没在密度为0.9×103 kg/m3的液体中时,测力计的示数变为3.2 N。金属零件在液体中受到的浮力是
N,其体积为 m3。(g取10 N/kg)
7.某热气球充气后体积为3000 m3,则该热气球所受的浮力为 N。(g取10 N/kg,空气的密度取1.29 kg/m3)
8.(2021云南)某小组探究“浮力的大小与排开液体所受重力的关系”。
(1)实验步骤如图①所示,图甲、乙、丁、戊中弹簧测力计的示数分别为F1、F2、F3、F4。由图甲和图丁可知物体受到的浮力F浮= 。
(2)下列选项中若 (填字母)成立,则可以得出浮力的大小与排开液体所受重力的关系。
A.F1-F2=F3-F4
B.F1-F3=F4-F2
C.F3-F2=F1-F4
(3)另一小组利用两个相同的弹簧测力计A和B、饮料瓶和吸管组成的溢水杯、薄塑料袋(质量忽略不计)对实验进行改进,装置如图②所示。向下移动水平横杆,使物体缓慢浸入盛满水的溢水杯中,观察到A的示数逐渐 ,B的示数逐渐 ,且A、B示数的变化量 (选填“相等”或“不相等”)。
(4)(多选)比较两种实验方案,改进后的实验方案的优点是 。
A.测力计A的示数就是物体所受浮力的大小
B.实验器材生活化,测力计固定、示数更稳定
C.能同步观察测力计A、B示数的变化
9.如图所示,两个完全相同的盛水容器放在盘秤上,用细线悬挂质量相同的实心铅球和铝球(ρ铅>ρ铝),当它们全部浸入水中时,容器内的水面高度相同,设绳子的拉力分别为F1和F2,盘秤的示数分别为F1'和F2',则 ( )
A.F1=F2 F1'=F2' B.F1F2'
C.F1>F2 F1'=F2' D.F1>F2 F1'
第2课时 阿基米德原理的综合应用
1 比较浮力的大小
1.如图所示,两只相同的气球分别充入氢气和空气,充气后的体积相同,放飞气球时只有氢气气球升到空中。若它们在空气中受到的浮力分别为F氢和F空,则下列说法中正确的是 ( )
A.F氢>F空 B.F氢=F空
C.F氢2.(2021衡阳)甲、乙、丙、丁是四个体积、形状相同而材质不同的小球,把它们放入水中静止后的情况如图0所示,则它们在水中所受浮力相等的是 ( )
图0
A.甲和乙 B.乙和丙
C.丙和丁 D.甲和丁
3.已知铜的密度大于铝的密度,如果把两个质量相同的实心铜球和铝球全部按入水中,那么两球所受浮力的大小关系为 ( )
A.铜球比铝球的小 B.铜球比铝球的大
C.两球一样大 D.无法确定
4.已知铜的密度大于铁的密度,水的密度大于煤油的密度,有两个质量相同的实心铜球和铁球,如果把铜球浸没在煤油中,铁球浸没在水中,那么两者所受浮力的大小关系为( )
A.铜球比铁球的小 B.铜球比铁球的大
C.两球一样大 D.无法确定
5.如图1所示,在三个相同的容器中盛有质量相等的不同种类的液体,将三个相同的铁球甲、乙、丙分别下沉到各容器底部,当铁球静止时,试比较三个容器内的铁球受到的浮力 ( )
图1
A.甲最小 B.乙最小
C.丙最小 D.大小一样
6.如图2所示,有铜、铁、铝三个实心球(ρ铜>ρ铁>ρ铝),用细线拴住,当它们浸没在水中时,三根细线上的拉力大小相等,则关于这三个金属球的体积、质量之间的关系,下列判断正确的是 ( )
图2
A.V铜>V铁>V铝,m铜>m铁>m铝 B.V铜>V铁>V铝,m铜C.V铜m铁>m铝 D.V铜2 阿基米德原理的综合应用
7.铁块的体积是50 cm3,浸没于水中时排开水的体积是 m3,排开的水重为 N,受到的浮力是 N。若铁块的一半体积浸在煤油中,则它受到的浮力是 N。(ρ水=1.0×
103 kg/m3,ρ煤油=0.8×103 kg/m3,g取10 N/kg)
8.如图3所示,已知木块的重力为3 N,体积为500 cm3,当木块静止时,细线的拉力为2.5 N,
g取10 N/kg,则木块受到的浮力为 N,液体的密度是 kg/m3。
图3
9.一个质量为80 g的金属块,浸没在盛满酒精的烧杯中时,从杯中溢出了10 g酒精。求:(ρ酒精=
0.8×103 kg/m3,g取10 N/kg)
(1)该金属块所受的浮力。
(2)该金属块的体积。
(3)如果把该金属块浸没在盛满水的烧杯中,那么此时该金属块受到的浮力大小是多少。
10.在弹簧测力计下悬挂一个金属零件,示数是2.7 N。当把零件浸没在水中时,弹簧测力计的示数是1.7 N。现把该零件浸没在另一种液体中时,弹簧测力计的示数是1.9 N。求:(g取
10 N/kg)
(1)该零件浸没在水中时受到的浮力。
(2)该金属零件的密度。
(3)另一种液体的密度。
11.(2020百色)如图4所示,将悬挂在弹簧测力计上的实心铝球浸没在装满水的溢水杯中,铝球静止时,弹簧测力计的示数为3.4 N,已知水的密度ρ水=1.0×103 kg/m3,铝的密度ρ铝=2.7×
103 kg/m3,则铝球的体积为 m3,铝球浸没在水中时所受的浮力为 N。(g取10 N/kg)
图4
12.(2020柳州)如图5所示是某商场前竖立的大型充气金箍棒。为估算它受到空气浮力的大小,将其视为底面半径r=1 m、高h=10 m的圆柱体。两名同学提出两种不同的方法,甲方法:根据它上、下表面受到大气的压力差计算浮力。乙方法:根据阿基米德原理计算浮力。已知海拔2000 m以内,每升高10 m大气压降低110 Pa,地面附近的空气密度约为ρ=1.3 kg/m3,π取3.14,g取10 N/kg。
(1)请你用以上两种方法,分别计算该充气金箍棒受到浮力的大小。
(2)不考虑上述两种方法计算结果的差异,对于估算空气中物体受到浮力的大小,你认为哪种方法适用范围更广 请简述理由。
第1课时
1.A [解析] 圆柱体未接触水面时,拉力等于其重力,则弹簧测力计的示数不变;当圆柱体下表面逐渐浸入水中时,圆柱体排开水的体积增大,所受的浮力增大,弹簧测力计的示数减小;圆柱体浸没后,所受的浮力不变,则弹簧测力计的示数不变。
2.(1)4 (2)①1 ②a d ③大 ④无
(3)没有控制排开液体的体积相同
[解析] (1)由题意可知,用手把饮料罐按入水中,手会感受到竖直向上的浮力,饮料罐浸入水中越深,饮料罐排开水的体积就越大,手会感到越吃力,说明浮力越大,故可以支持猜想4。
(2)①在序号a的实验中物体所受的浮力:F浮水=G-F=4 N-3 N=1 N。
②为了得出初步结论“浮力大小与液体密度有关”,则要控制物体相同、排开液体的体积相同,仅改变液体的密度,故序号a、d、e三次实验符合要求。
③在序号a的实验中物体所受的浮力:F浮水=G-F=4 N-3 N=1 N;在序号d的实验中物体所受的浮力:F浮酒=G-F'=4 N-3.2 N=0.8 N;在序号e的实验中物体所受的浮力:F浮盐=G-F″=4 N-2.8 N=
1.2 N。由此可知,同一物体浸没在浓盐水中时受到的浮力较大,浸没在酒精中时受到的浮力较小。又因为盐水的密度较大,酒精的密度较小,所以可以得出结论:在其他条件相同时,液体的密度越大,物体所受的浮力越大。
④在a、b、c三次实验中,控制了物体的形状、排开液体的体积和液体的密度相同,仅改变了物体的重力,根据称重法F浮=G-F,可以计算出物体所受的浮力都为1 N,故可以得出结论:浮力的大小与物体的重力无关。
(3)要研究浮力大小与物体形状的关系,根据控制变量法可知,要控制物体排开液体的体积和液体的密度不变,仅改变物体的形状。小明的实验中虽然改变了物体的形状,但没有控制排开液体的体积相同,故小明的结论不可靠。
3.B
4.C [解析] 由题意可知,烧杯中盛有水但不满,从杯中溢出了0.6 N的水,说明物体排开的水的重力应大于0.6 N,根据阿基米德原理可知,物体受到的浮力大于0.6 N。
5.2 3
[解析] 根据阿基米德原理可得,F浮=ρ水gV排=1.0×103 kg/m3×10 N/kg×0.2×10-3 m3=2 N;物体静止时,处于平衡状态,对物体受力分析,物体受重力、浮力和拉力的作用,即G=F浮+F拉,则F拉=
G-F浮=5 N-2 N=3 N。
6.1.8 2×10-4 [解析] 零件的重力:G=F示1=5 N,零件所受的浮力:F浮=G-F示2=5 N-3.2 N=
1.8 N;零件的体积:V零=V排===2×10-4 m3。
7.3.87×104
[解析] 热气球所受的浮力为F浮=ρ空气gV排=1.29 kg/m3×10 N/kg×3000 m3=3.87×104 N。
8.(1)F1-F3 (2)B
(3)变小 变大 相等
(4)BC
[解析] (1)由图知物体的重力为F1,物体浸没时弹簧测力计的示数为F3,则物体受到的浮力
F浮=F1-F3。
(2)由图乙可知空烧杯的重力为F2,由图戊可知物体浸没时排开的液体与烧杯的总重力为F4,则物体浸没时排开液体的重力G排=F4-F2,F浮=F1-F3,若F1-F3=F4-F2成立,说明物体受到浮力的大小与物体排开液体所受的重力相等。
(3)由图可知,向下移动水平横杆,使物体缓慢浸入盛满水的溢水杯中,物体排开水的体积变大,受到的浮力变大,由称重法F浮=G-F可知,弹簧测力计A的示数变小,物体排开水的体积越大,薄塑料袋内水的重力越大,即弹簧测力计B的示数越大,薄塑料袋的质量忽略不计,由阿基米德原理可知,弹簧测力计A、B示数的变化量相等。
(4)比较两种实验方案可知,改进后:由称重法F浮=G-F可知,弹簧测力计A的示数等于物体的重力减去物体所受的浮力,故A错误;由图②的实验装置和器材(两个相同的弹簧测力计A和B、饮料瓶和吸管组成的溢水杯、薄塑料袋)可知,实验器材生活化,测力计固定、示数更稳定,故B正确;薄塑料袋质量不计,能同步观察测力计A、B示数的变化,从而得出物体受到浮力的大小与物体排开液体所受重力的关系,故C正确。
9.C [解析] 把容器、水和小球当作一个整体,整体受到向上的支持力、向上的拉力和向下的总重力,根据力的平衡条件可得F支+F拉=G容器+G水+G球,
压力和支持力是一对相互作用力,则盘秤受到的压力:F压=F支=G容器+G水+G球-F拉①,
以小球为研究对象,则受到向上的拉力:F拉=G球-F浮②,
由①②结合阿基米德原理可得,
F压=G容器+G水+F浮=G容器+G水+G排水=G容器+ρ水gV水+ρ水gV排水=G容器+ρ水g(V水+V排水)③,
因为液面高度相同、容器完全相同,则容器中的水和排开水的总体积相等,根据③式可知,盘秤受到的压力(即盘秤的示数)相同,即F1'=F2'。
对于悬吊在水中的小球来说,它受到自身的重力G球、水对它的浮力F浮和细线对它的拉力
F拉三个力的作用而处于平衡状态,则三个力之间的关系为F拉=G球-F浮,由题知两球是质量相等的实心球,故G1=G2,由于铅的密度大于铝的密度,根据密度的变形式V=可知,铅球的体积小于铝球的体积;两球均浸没于水中,则铅球排开水的体积较小,由F浮=ρ水gV排可知,铅球所受水的浮力F浮1小于铝球所受水的浮力F浮2,由F拉=G球-F浮可知,F1>F2。
第2课时
1.B [解析] 由于两气球是“浸没”在空气中的,且它们的体积相同,即它们排开空气的体积相同,根据F浮=ρ空气gV排可知,两球所受浮力相同。
2.C [解析] 由图可知,四个小球排开水的体积关系为V甲3.A [解析] 已知m铜=m铝,ρ铜>ρ铝,由ρ=可知,V铜V物,即V铜排4.A [解析] 已知m铜=m铁,ρ铜>ρ铁,由ρ=可知,V铜5.A [解析] 由图可知V甲液>V丙液>V乙液,又因为m甲液=m丙液=m乙液,所以由ρ=可得,三容器中液体的密度:ρ甲液<ρ丙液<ρ乙液;三个铁球的体积相同,所以浸没时排开液体的体积相同,又因为
ρ甲液<ρ丙液<ρ乙液,根据F浮=ρ液gV排可知,三个铁球受到的浮力:F甲浮6.D [解析] 实心球浸没在水中有F拉+F浮=G,所以F拉=G-F浮=ρ球V球g-ρ水V球g=
(ρ球-ρ水)V球g,因为ρ铜>ρ铁>ρ铝,拉力F拉相同,所以V铜F铜7.5×10-5 0.5 0.5 0.2
[解析] 浸没时,V排=V铁=50 cm3=5×10-5 m3,所以G排=ρ水gV排=1.0×103 kg/m3×10 N/kg×5×
10-5m3=0.5 N,F浮=G排=0.5 N。若铁块的一半体积浸在煤油中,则其受到的浮力:F浮'=ρ煤油g=
0.8×103 kg/m3×10 N/kg×=0.2 N。
8.5.5 1.1×103
[解析] 木块受到的浮力为F浮=G+F拉=3 N+2.5 N=5.5 N;又因为F浮=ρ液gV排,所以液体的密度为ρ液===1.1×103 kg/m3。
9.(1)由阿基米德原理可得,
该金属块所受的浮力:
F浮=G排=m排g=0.01 kg×10 N/kg=0.1 N。
(2)溢出酒精的体积:
V溢酒精===12.5 cm3,
因为金属块浸没在酒精中,所以金属块的体积:
V=V溢酒精=12.5 cm3。
(3)该金属块浸没在盛满水的烧杯中时,排开水的体积:
V排=V=12.5 cm3=1.25×10-5 m3,
此时金属块受到的浮力:F浮'=ρ水 gV排=1.0×103 kg/m3×10 N/kg×1.25×10-5 m3=0.125 N。
10.(1)该零件浸没在水中时受到的浮力:
F浮=G-F示1=2.7 N-1.7 N=1 N。
(2)金属零件的体积:
V=V排===1×10-4 m3,
金属零件的质量:m===0.27 kg,
金属零件的密度:
ρ金属===2.7×103 kg/m3。
(3)金属零件浸没在另一种液体中时受到的浮力:
F浮'=G-F示2=2.7 N-1.9 N=0.8 N,
另一种液体的密度:
ρ液===0.8×103 kg/m3。
11.2×10-4 2 [解析] 实心铝球浸没在水中静止时,排开水的体积V排=V球,则铝球受到的浮力F浮=ρ水gV排=ρ水gV球,实心铝球的重力G=mg=ρ铝gV球;由于铝球受力平衡,则有G=F浮+F拉,即ρ铝gV球=ρ水gV球+F拉,代入数据,2.7×103 kg/m3×10 N/kg×V球=1.0×103 kg/m3×10 N/kg×
V球+3.4 N,解得铝球的体积:V球=2×10-4 m3;铝球浸没时受到的浮力:F浮=ρ水gV排=1.0×
103 kg/m3×10 N/kg×2×10-4 m3=2 N。
12.(1)甲方法,大型充气金箍棒受到的浮力:
F浮=F向上-F向下=(p向上-p向下)S=Δpπr2=110 Pa×3.14×(1 m)2=345.4 N。
乙方法,大型充气金箍棒受到的浮力:
F浮=ρgV排=ρgSh=ρgπr2h=1.3 kg/m3×10 N/kg×3.14×(1 m)2×10 m=408.2 N。
(2)根据阿基米德原理计算浮力的乙方法适用范围更广。
理由:如果物体的上、下表面不是水平的,不便于测量上、下表面的面积,不便于计算上、下表面的压力差和浮力。
第1课时 阿基米德原理的简单应用
1 影响浮力大小的因素
1.如图所示,把挂在弹簧测力计下的金属圆柱体缓慢浸入水中(水足够深),在圆柱体接触容器底之前,图中能正确反映弹簧测力计示数F和圆柱体下降高度h关系的图像是
( )
2.在“探究浮力的大小跟哪些因素有关”的实验中,小明提出如下猜想:
猜想1:浮力的大小可能与液体密度有关;
猜想2:浮力的大小可能与物体重力有关;
猜想3:浮力的大小可能与物体形状有关;
猜想4:浮力的大小可能与排开液体的体积有关。
(1)如图所示,用手把饮料罐按入水中,饮料罐浸入水中越深,手会感到越吃力。这个事实可以支持以上猜想 (填数字)。
(2)为了研究猜想1和猜想2,小明使用体积相同的A、B、C三个圆柱体,测得重力分别为4 N、4.5 N和5 N,然后进行如图所示的实验。
①在序号a的实验中,物体所受的浮力为 N。
②比较 、 、e三次实验,可得出初步结论:浮力大小与液体密度有关。
③进一步分析可知,在其他条件相同时,液体的密度越大,物体所受的浮力越 (选填“大”或“小”)。
④比较a、b、c三次实验,可得出结论:浮力的大小与物体的重力 (选填“有”或“无”)关。
(3)为了研究猜想3,小明用两块相同的橡皮泥分别捏成圆锥体和圆柱体进行如图所示的实验,由此小明得出结论:浮力的大小与物体的形状有关。小珍认为该结论不可靠,主要原因是
。
2 阿基米德原理
3.将一个重为10 N的物体放入一装满水的溢水杯中,从杯中溢出3 N的水,则物体在水中受到的浮力大小为 ( )
A.10 N B.3 N
C.13 N D.7 N
4.将一个重为1 N的物体放入一盛有水但不满的烧杯中,从杯中溢出了0.6 N的水,则物体受到的浮力 ( )
A.等于1 N B.等于0.6 N
C.一定大于0.6 N D.无法确定
5.(2020黔南州)如图所示,重为5 N、体积为0.2×10-3 m3的物体用细线系在弹簧测力计的挂钩上,将它浸没在水中,物体受到的浮力是 N, 静止时弹簧测力计的示数是 N。(g取10 N/kg)
6.(2021益阳)在弹簧测力计下端悬挂一个金属零件,测力计的示数是5 N。当把零件浸没在密度为0.9×103 kg/m3的液体中时,测力计的示数变为3.2 N。金属零件在液体中受到的浮力是
N,其体积为 m3。(g取10 N/kg)
7.某热气球充气后体积为3000 m3,则该热气球所受的浮力为 N。(g取10 N/kg,空气的密度取1.29 kg/m3)
8.(2021云南)某小组探究“浮力的大小与排开液体所受重力的关系”。
(1)实验步骤如图①所示,图甲、乙、丁、戊中弹簧测力计的示数分别为F1、F2、F3、F4。由图甲和图丁可知物体受到的浮力F浮= 。
(2)下列选项中若 (填字母)成立,则可以得出浮力的大小与排开液体所受重力的关系。
A.F1-F2=F3-F4
B.F1-F3=F4-F2
C.F3-F2=F1-F4
(3)另一小组利用两个相同的弹簧测力计A和B、饮料瓶和吸管组成的溢水杯、薄塑料袋(质量忽略不计)对实验进行改进,装置如图②所示。向下移动水平横杆,使物体缓慢浸入盛满水的溢水杯中,观察到A的示数逐渐 ,B的示数逐渐 ,且A、B示数的变化量 (选填“相等”或“不相等”)。
(4)(多选)比较两种实验方案,改进后的实验方案的优点是 。
A.测力计A的示数就是物体所受浮力的大小
B.实验器材生活化,测力计固定、示数更稳定
C.能同步观察测力计A、B示数的变化
9.如图所示,两个完全相同的盛水容器放在盘秤上,用细线悬挂质量相同的实心铅球和铝球(ρ铅>ρ铝),当它们全部浸入水中时,容器内的水面高度相同,设绳子的拉力分别为F1和F2,盘秤的示数分别为F1'和F2',则 ( )
A.F1=F2 F1'=F2' B.F1
C.F1>F2 F1'=F2' D.F1>F2 F1'
第2课时 阿基米德原理的综合应用
1 比较浮力的大小
1.如图所示,两只相同的气球分别充入氢气和空气,充气后的体积相同,放飞气球时只有氢气气球升到空中。若它们在空气中受到的浮力分别为F氢和F空,则下列说法中正确的是 ( )
A.F氢>F空 B.F氢=F空
C.F氢
图0
A.甲和乙 B.乙和丙
C.丙和丁 D.甲和丁
3.已知铜的密度大于铝的密度,如果把两个质量相同的实心铜球和铝球全部按入水中,那么两球所受浮力的大小关系为 ( )
A.铜球比铝球的小 B.铜球比铝球的大
C.两球一样大 D.无法确定
4.已知铜的密度大于铁的密度,水的密度大于煤油的密度,有两个质量相同的实心铜球和铁球,如果把铜球浸没在煤油中,铁球浸没在水中,那么两者所受浮力的大小关系为( )
A.铜球比铁球的小 B.铜球比铁球的大
C.两球一样大 D.无法确定
5.如图1所示,在三个相同的容器中盛有质量相等的不同种类的液体,将三个相同的铁球甲、乙、丙分别下沉到各容器底部,当铁球静止时,试比较三个容器内的铁球受到的浮力 ( )
图1
A.甲最小 B.乙最小
C.丙最小 D.大小一样
6.如图2所示,有铜、铁、铝三个实心球(ρ铜>ρ铁>ρ铝),用细线拴住,当它们浸没在水中时,三根细线上的拉力大小相等,则关于这三个金属球的体积、质量之间的关系,下列判断正确的是 ( )
图2
A.V铜>V铁>V铝,m铜>m铁>m铝 B.V铜>V铁>V铝,m铜
7.铁块的体积是50 cm3,浸没于水中时排开水的体积是 m3,排开的水重为 N,受到的浮力是 N。若铁块的一半体积浸在煤油中,则它受到的浮力是 N。(ρ水=1.0×
103 kg/m3,ρ煤油=0.8×103 kg/m3,g取10 N/kg)
8.如图3所示,已知木块的重力为3 N,体积为500 cm3,当木块静止时,细线的拉力为2.5 N,
g取10 N/kg,则木块受到的浮力为 N,液体的密度是 kg/m3。
图3
9.一个质量为80 g的金属块,浸没在盛满酒精的烧杯中时,从杯中溢出了10 g酒精。求:(ρ酒精=
0.8×103 kg/m3,g取10 N/kg)
(1)该金属块所受的浮力。
(2)该金属块的体积。
(3)如果把该金属块浸没在盛满水的烧杯中,那么此时该金属块受到的浮力大小是多少。
10.在弹簧测力计下悬挂一个金属零件,示数是2.7 N。当把零件浸没在水中时,弹簧测力计的示数是1.7 N。现把该零件浸没在另一种液体中时,弹簧测力计的示数是1.9 N。求:(g取
10 N/kg)
(1)该零件浸没在水中时受到的浮力。
(2)该金属零件的密度。
(3)另一种液体的密度。
11.(2020百色)如图4所示,将悬挂在弹簧测力计上的实心铝球浸没在装满水的溢水杯中,铝球静止时,弹簧测力计的示数为3.4 N,已知水的密度ρ水=1.0×103 kg/m3,铝的密度ρ铝=2.7×
103 kg/m3,则铝球的体积为 m3,铝球浸没在水中时所受的浮力为 N。(g取10 N/kg)
图4
12.(2020柳州)如图5所示是某商场前竖立的大型充气金箍棒。为估算它受到空气浮力的大小,将其视为底面半径r=1 m、高h=10 m的圆柱体。两名同学提出两种不同的方法,甲方法:根据它上、下表面受到大气的压力差计算浮力。乙方法:根据阿基米德原理计算浮力。已知海拔2000 m以内,每升高10 m大气压降低110 Pa,地面附近的空气密度约为ρ=1.3 kg/m3,π取3.14,g取10 N/kg。
(1)请你用以上两种方法,分别计算该充气金箍棒受到浮力的大小。
(2)不考虑上述两种方法计算结果的差异,对于估算空气中物体受到浮力的大小,你认为哪种方法适用范围更广 请简述理由。
第1课时
1.A [解析] 圆柱体未接触水面时,拉力等于其重力,则弹簧测力计的示数不变;当圆柱体下表面逐渐浸入水中时,圆柱体排开水的体积增大,所受的浮力增大,弹簧测力计的示数减小;圆柱体浸没后,所受的浮力不变,则弹簧测力计的示数不变。
2.(1)4 (2)①1 ②a d ③大 ④无
(3)没有控制排开液体的体积相同
[解析] (1)由题意可知,用手把饮料罐按入水中,手会感受到竖直向上的浮力,饮料罐浸入水中越深,饮料罐排开水的体积就越大,手会感到越吃力,说明浮力越大,故可以支持猜想4。
(2)①在序号a的实验中物体所受的浮力:F浮水=G-F=4 N-3 N=1 N。
②为了得出初步结论“浮力大小与液体密度有关”,则要控制物体相同、排开液体的体积相同,仅改变液体的密度,故序号a、d、e三次实验符合要求。
③在序号a的实验中物体所受的浮力:F浮水=G-F=4 N-3 N=1 N;在序号d的实验中物体所受的浮力:F浮酒=G-F'=4 N-3.2 N=0.8 N;在序号e的实验中物体所受的浮力:F浮盐=G-F″=4 N-2.8 N=
1.2 N。由此可知,同一物体浸没在浓盐水中时受到的浮力较大,浸没在酒精中时受到的浮力较小。又因为盐水的密度较大,酒精的密度较小,所以可以得出结论:在其他条件相同时,液体的密度越大,物体所受的浮力越大。
④在a、b、c三次实验中,控制了物体的形状、排开液体的体积和液体的密度相同,仅改变了物体的重力,根据称重法F浮=G-F,可以计算出物体所受的浮力都为1 N,故可以得出结论:浮力的大小与物体的重力无关。
(3)要研究浮力大小与物体形状的关系,根据控制变量法可知,要控制物体排开液体的体积和液体的密度不变,仅改变物体的形状。小明的实验中虽然改变了物体的形状,但没有控制排开液体的体积相同,故小明的结论不可靠。
3.B
4.C [解析] 由题意可知,烧杯中盛有水但不满,从杯中溢出了0.6 N的水,说明物体排开的水的重力应大于0.6 N,根据阿基米德原理可知,物体受到的浮力大于0.6 N。
5.2 3
[解析] 根据阿基米德原理可得,F浮=ρ水gV排=1.0×103 kg/m3×10 N/kg×0.2×10-3 m3=2 N;物体静止时,处于平衡状态,对物体受力分析,物体受重力、浮力和拉力的作用,即G=F浮+F拉,则F拉=
G-F浮=5 N-2 N=3 N。
6.1.8 2×10-4 [解析] 零件的重力:G=F示1=5 N,零件所受的浮力:F浮=G-F示2=5 N-3.2 N=
1.8 N;零件的体积:V零=V排===2×10-4 m3。
7.3.87×104
[解析] 热气球所受的浮力为F浮=ρ空气gV排=1.29 kg/m3×10 N/kg×3000 m3=3.87×104 N。
8.(1)F1-F3 (2)B
(3)变小 变大 相等
(4)BC
[解析] (1)由图知物体的重力为F1,物体浸没时弹簧测力计的示数为F3,则物体受到的浮力
F浮=F1-F3。
(2)由图乙可知空烧杯的重力为F2,由图戊可知物体浸没时排开的液体与烧杯的总重力为F4,则物体浸没时排开液体的重力G排=F4-F2,F浮=F1-F3,若F1-F3=F4-F2成立,说明物体受到浮力的大小与物体排开液体所受的重力相等。
(3)由图可知,向下移动水平横杆,使物体缓慢浸入盛满水的溢水杯中,物体排开水的体积变大,受到的浮力变大,由称重法F浮=G-F可知,弹簧测力计A的示数变小,物体排开水的体积越大,薄塑料袋内水的重力越大,即弹簧测力计B的示数越大,薄塑料袋的质量忽略不计,由阿基米德原理可知,弹簧测力计A、B示数的变化量相等。
(4)比较两种实验方案可知,改进后:由称重法F浮=G-F可知,弹簧测力计A的示数等于物体的重力减去物体所受的浮力,故A错误;由图②的实验装置和器材(两个相同的弹簧测力计A和B、饮料瓶和吸管组成的溢水杯、薄塑料袋)可知,实验器材生活化,测力计固定、示数更稳定,故B正确;薄塑料袋质量不计,能同步观察测力计A、B示数的变化,从而得出物体受到浮力的大小与物体排开液体所受重力的关系,故C正确。
9.C [解析] 把容器、水和小球当作一个整体,整体受到向上的支持力、向上的拉力和向下的总重力,根据力的平衡条件可得F支+F拉=G容器+G水+G球,
压力和支持力是一对相互作用力,则盘秤受到的压力:F压=F支=G容器+G水+G球-F拉①,
以小球为研究对象,则受到向上的拉力:F拉=G球-F浮②,
由①②结合阿基米德原理可得,
F压=G容器+G水+F浮=G容器+G水+G排水=G容器+ρ水gV水+ρ水gV排水=G容器+ρ水g(V水+V排水)③,
因为液面高度相同、容器完全相同,则容器中的水和排开水的总体积相等,根据③式可知,盘秤受到的压力(即盘秤的示数)相同,即F1'=F2'。
对于悬吊在水中的小球来说,它受到自身的重力G球、水对它的浮力F浮和细线对它的拉力
F拉三个力的作用而处于平衡状态,则三个力之间的关系为F拉=G球-F浮,由题知两球是质量相等的实心球,故G1=G2,由于铅的密度大于铝的密度,根据密度的变形式V=可知,铅球的体积小于铝球的体积;两球均浸没于水中,则铅球排开水的体积较小,由F浮=ρ水gV排可知,铅球所受水的浮力F浮1小于铝球所受水的浮力F浮2,由F拉=G球-F浮可知,F1>F2。
第2课时
1.B [解析] 由于两气球是“浸没”在空气中的,且它们的体积相同,即它们排开空气的体积相同,根据F浮=ρ空气gV排可知,两球所受浮力相同。
2.C [解析] 由图可知,四个小球排开水的体积关系为V甲
ρ甲液<ρ丙液<ρ乙液,根据F浮=ρ液gV排可知,三个铁球受到的浮力:F甲浮
(ρ球-ρ水)V球g,因为ρ铜>ρ铁>ρ铝,拉力F拉相同,所以V铜
[解析] 浸没时,V排=V铁=50 cm3=5×10-5 m3,所以G排=ρ水gV排=1.0×103 kg/m3×10 N/kg×5×
10-5m3=0.5 N,F浮=G排=0.5 N。若铁块的一半体积浸在煤油中,则其受到的浮力:F浮'=ρ煤油g=
0.8×103 kg/m3×10 N/kg×=0.2 N。
8.5.5 1.1×103
[解析] 木块受到的浮力为F浮=G+F拉=3 N+2.5 N=5.5 N;又因为F浮=ρ液gV排,所以液体的密度为ρ液===1.1×103 kg/m3。
9.(1)由阿基米德原理可得,
该金属块所受的浮力:
F浮=G排=m排g=0.01 kg×10 N/kg=0.1 N。
(2)溢出酒精的体积:
V溢酒精===12.5 cm3,
因为金属块浸没在酒精中,所以金属块的体积:
V=V溢酒精=12.5 cm3。
(3)该金属块浸没在盛满水的烧杯中时,排开水的体积:
V排=V=12.5 cm3=1.25×10-5 m3,
此时金属块受到的浮力:F浮'=ρ水 gV排=1.0×103 kg/m3×10 N/kg×1.25×10-5 m3=0.125 N。
10.(1)该零件浸没在水中时受到的浮力:
F浮=G-F示1=2.7 N-1.7 N=1 N。
(2)金属零件的体积:
V=V排===1×10-4 m3,
金属零件的质量:m===0.27 kg,
金属零件的密度:
ρ金属===2.7×103 kg/m3。
(3)金属零件浸没在另一种液体中时受到的浮力:
F浮'=G-F示2=2.7 N-1.9 N=0.8 N,
另一种液体的密度:
ρ液===0.8×103 kg/m3。
11.2×10-4 2 [解析] 实心铝球浸没在水中静止时,排开水的体积V排=V球,则铝球受到的浮力F浮=ρ水gV排=ρ水gV球,实心铝球的重力G=mg=ρ铝gV球;由于铝球受力平衡,则有G=F浮+F拉,即ρ铝gV球=ρ水gV球+F拉,代入数据,2.7×103 kg/m3×10 N/kg×V球=1.0×103 kg/m3×10 N/kg×
V球+3.4 N,解得铝球的体积:V球=2×10-4 m3;铝球浸没时受到的浮力:F浮=ρ水gV排=1.0×
103 kg/m3×10 N/kg×2×10-4 m3=2 N。
12.(1)甲方法,大型充气金箍棒受到的浮力:
F浮=F向上-F向下=(p向上-p向下)S=Δpπr2=110 Pa×3.14×(1 m)2=345.4 N。
乙方法,大型充气金箍棒受到的浮力:
F浮=ρgV排=ρgSh=ρgπr2h=1.3 kg/m3×10 N/kg×3.14×(1 m)2×10 m=408.2 N。
(2)根据阿基米德原理计算浮力的乙方法适用范围更广。
理由:如果物体的上、下表面不是水平的,不便于测量上、下表面的面积,不便于计算上、下表面的压力差和浮力。
同课章节目录
- 第一章 打开物理世界的大门
- 第一节 走进神奇
- 第二节 探索之路
- 第三节 站在巨人的肩膀上
- 第二章 运动的世界
- 第一节 动与静
- 第二节 长度与时间的测量
- 第三节 快与慢
- 第四节 科学探究:速度的变化
- 第三章 声的世界
- 第一节 科学探究:声音的产生与传播
- 第二节 声音的特性
- 第三节 超声与次声
- 第四章 多彩的光
- 第一节 光的反射
- 第二节 平面镜成像
- 第三节 光的折射
- 第四节 光的色散
- 第五节 科学探究:凸透镜成像
- 第六节 神奇的眼睛
- 第五章 质量与密度
- 第一节 质量
- 第二节 学习使用天平和量筒
- 第三节 科学探究:物质的密度
- 第四节 密度知识的应用
- 第六章 熟悉而陌生的力
- 第一节 力
- 第二节 怎样描述力
- 第三节 弹力与弹簧测力计
- 第四节 来自地球的力
- 第五节 科学探究:摩擦力
- 第七章 力与运动
- 第一节 科学探究:牛顿第一定律
- 第二节 力的合成
- 第三节 力的平衡
- 第八章 压强
- 第一节 压力的作用效果
- 第二节 科学探究:液体的压强
- 第三节 空气的“力量”
- 第四节 流体压强与流速的关系
- 第九章 浮力
- 第一节 认识浮力
- 第二节 阿基米德原理
- 第三节 物体的浮与沉
- 第十章 机械与人
- 第一节 科学探究:杠杆的平衡条件
- 第二节 滑轮及其应用
- 第三节 做功了吗
- 第四节 做功的快慢
- 第五节 机械效率
- 第六节 合理利用机械能
- 第十一章 小粒子与大宇宙
- 第一节 走进微观
- 第二节 看不见的运动
- 第三节 探索宇宙
