20.1.2 加权平均数 课件(共21张PPT)
文档属性
| 名称 | 20.1.2 加权平均数 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 07:13:41 | ||
图片预览








文档简介
(共21张PPT)
2022年春华师大版数学
八年级下册数学精品课件
20.1.2 加权平均数
学习目标
理解数据的加权平均数的概念及求法.
会用加权平均数分析一组数据的集中趋势.
1. 算术平均数:
一组数据的总和与这组数据的个数之比叫做这组数据的算术平均数.
2. 计算公式:
x =
x1+x2+ x3+ ··· + xn
n
3. 算术平均数:
是反映一组数据中数据总体的平均大小情况的量.
4. 计算器操作:
开机、
清除、
输数据、
读信息.
选择功能、
复习回顾
老师对同学们每学期总评成绩是这样做的: 平时成绩占40%,考试成绩占60%. 某同学平时成绩70 分,考试成绩90分, 那么如何来评定该同学的学期总评成绩呢
解:
该同学的学期总评成绩是:
70×40%
=82(分)
+
90×60%
加权平均数
权 重
权重的意义:
各个数据在该组数据中所占有的不同重要性的反映.
加权平均数的意义:
按各个数据的权重来反映该组数据的总体平均大小情况.
问题引入
加权平均数
在实际问题中,一组数据里的各个数据的“重要程度”未必相同。因而,在计算这组数据时往往给每个数据一个“权 ”.
x1
f1
f1
f2
fk
加权平均数:一般说来,如果在n个数中, 出现 次,
出现 次,… 出现 次 ( ),
其中
叫做权.
x2 f2 xk fk f1+f2+…+fk=n
x = (x1 f1+x2 f2+…+xk fk)
n
1
“权”越大,对平均数的影响就越大.
知识精讲
例1 一家公司打算招聘一名英文翻译.对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
典例解析
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
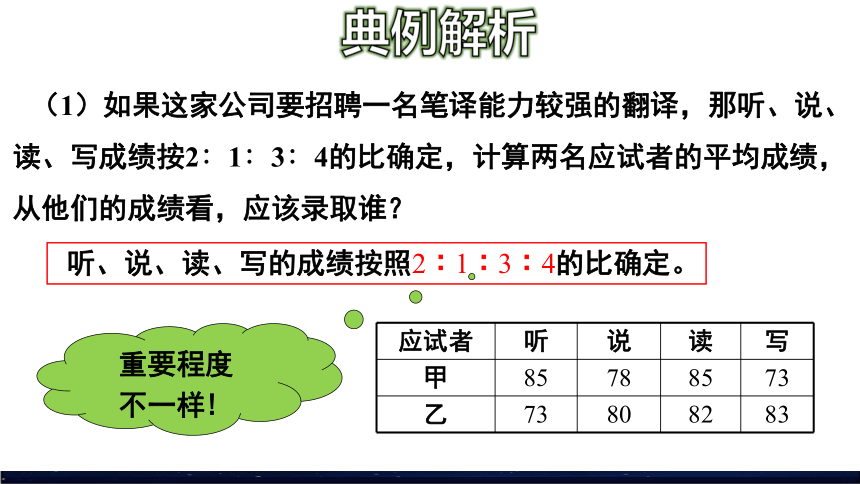
听、说、读、写的成绩按照2︰1︰3︰4的比确定。
重要程度
不一样!
(1)如果这家公司要招聘一名笔译能力较强的翻译,那听、说、读、写成绩按2∶1∶3∶4的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
典例解析
典例解析
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
2︰1︰3︰4
因为乙的成绩比甲高,所以应该录取乙。
解:
4
3
1
2
权
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
听、说、读、写的成绩按照3︰3︰2︰2的比确定。
重要程度
也不一样!
(2)如果这家公司要招聘一名口语能力比较强的翻译,听、说、读、写成绩按3∶3∶2∶2的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
典例解析
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
3︰3︰2︰2
因为甲的成绩比乙高,所以应该录取甲。
解: ,
2
2
3
3
权
典例解析
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
例2 一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示,请确定两人的名次。
典例解析
分析:这个问题可以看成是求两名选手三项成绩的加权平均数,50%、40%、10%说明演讲内容、演讲能力、演讲效果三项成绩在总成绩中的重要程度,是三项成绩的权。
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
典例解析
典例解析
解:选手A的最后得分是
选手B的最后得分是
由上可知选手B获得第一名,选手A获得第二名。
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
1.某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是
(A)84 (B) 86 (C) 88 (D) 90
( D )
2.若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是
A:(x+y)/2 B:(x+y)/(m+n)
C:(mx+ny)/(x+y) D:(mx+ny)/(m+n)
( D )
达标检测
3.已知数据a1,a2,a3的平均数是a,那么数据2a1+1,2a2+1,2a3+1 的平均数是
(A) a (B)2a (C) 2a+1 (D) 2a/3+1
4.一组6个数1,2,3,x, y, z 的平均数是 4
(1)求x, y, z 三数的平均数;
解:由题意可得(1+2+3+x+y+z)/6=4
即 1+2+3+x+y+z=24 ,所以 x+y+z=18
所以 (x+y+z)/3=18/3=6
( C )
(2)求 4x+5, 4y+6, 4z+7 的平均数.
达标检测
D
5.已知:x1,x2,x3… x10的平均数是a, x11,x12,x13… x30的平均数是b,则x1,x2,x3… x30的平均数是( )
(A) (a+b) (B) (a+b)
(C) (10a+30b)
(D) (10a+20b)
(1)则数据x1+3,x2 +3 … xn +3的平均数________.
(2)则数据10x1,10x2 … 10xn 的平均数________.
a+3
10a
6.若x1,x2.......xn的平均数是a
达标检测
考试 平时1 平时2 平时3 期中 期末
成绩 89 78 85 90 87
7.小明同学在初二年级第一学期的数学成绩如下表格, 请按图示的平时、期中、期末的权重, 计算小明同学的学期总评成绩.
期中
30%
期末
60%
平时
10%
解:
先计算小明的平时成绩:
(89+78+85)÷3
= 84
再计算小明的总评成绩:
84×10%+ 90×30%+ 87×60%
= 87.6 (分)
达标检测
8.某公司对应聘者A、B、C、D进行面试时, 按三个方面给予打分如右表.你就公司主事身份探索下列问题:
⑴总分计算发现D最高, 故录用D.
这样的录用中,三个方面的权重各是多少
合理吗
项 目 占分 A B C D
专业知识 20 14 18 17 16
工作经验 20 18 16 14 16
仪表形象 20 12 11 14 14
⑵若设置上述三个方面的重要性之比为6:3:1, 那么这三个方面的权重分别是_________________, 该录用谁
60%
, 30%
, 10%
⑶若设置上述三个方面的重要性之比为10:7:3, 那么这三个方面的权重分别是_________________, 又该录用谁
50%
, 35%
, 15%
达标检测
33.33%
, 33.33%
, 33.33%
不合理,仪表形象没有专业知识和工作经验重要
B
B
1. 你能说说算术平均数与加权平均数的区别 和联系吗?
(2) 在实际问题中,各项权不相等时,计算平均数时就要采用加权平均数,当各项权相等时,计算平均数就要采用算术平均数.
(1) 算术平均数是加权平均数的一种特殊情况(它特殊在各项的权相等)
2. 加权平均数中“权”有几种表现形式?
(1) 整数的形式;
(2) 比的形式;
(3) 百分比的形式;
小结梳理
2022年春华师大版数学
八年级下册数学精品课件
20.1.2 加权平均数
学习目标
理解数据的加权平均数的概念及求法.
会用加权平均数分析一组数据的集中趋势.
1. 算术平均数:
一组数据的总和与这组数据的个数之比叫做这组数据的算术平均数.
2. 计算公式:
x =
x1+x2+ x3+ ··· + xn
n
3. 算术平均数:
是反映一组数据中数据总体的平均大小情况的量.
4. 计算器操作:
开机、
清除、
输数据、
读信息.
选择功能、
复习回顾
老师对同学们每学期总评成绩是这样做的: 平时成绩占40%,考试成绩占60%. 某同学平时成绩70 分,考试成绩90分, 那么如何来评定该同学的学期总评成绩呢
解:
该同学的学期总评成绩是:
70×40%
=82(分)
+
90×60%
加权平均数
权 重
权重的意义:
各个数据在该组数据中所占有的不同重要性的反映.
加权平均数的意义:
按各个数据的权重来反映该组数据的总体平均大小情况.
问题引入
加权平均数
在实际问题中,一组数据里的各个数据的“重要程度”未必相同。因而,在计算这组数据时往往给每个数据一个“权 ”.
x1
f1
f1
f2
fk
加权平均数:一般说来,如果在n个数中, 出现 次,
出现 次,… 出现 次 ( ),
其中
叫做权.
x2 f2 xk fk f1+f2+…+fk=n
x = (x1 f1+x2 f2+…+xk fk)
n
1
“权”越大,对平均数的影响就越大.
知识精讲
例1 一家公司打算招聘一名英文翻译.对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
典例解析
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
听、说、读、写的成绩按照2︰1︰3︰4的比确定。
重要程度
不一样!
(1)如果这家公司要招聘一名笔译能力较强的翻译,那听、说、读、写成绩按2∶1∶3∶4的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
典例解析
典例解析
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
2︰1︰3︰4
因为乙的成绩比甲高,所以应该录取乙。
解:
4
3
1
2
权
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
听、说、读、写的成绩按照3︰3︰2︰2的比确定。
重要程度
也不一样!
(2)如果这家公司要招聘一名口语能力比较强的翻译,听、说、读、写成绩按3∶3∶2∶2的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
典例解析
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
3︰3︰2︰2
因为甲的成绩比乙高,所以应该录取甲。
解: ,
2
2
3
3
权
典例解析
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
例2 一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示,请确定两人的名次。
典例解析
分析:这个问题可以看成是求两名选手三项成绩的加权平均数,50%、40%、10%说明演讲内容、演讲能力、演讲效果三项成绩在总成绩中的重要程度,是三项成绩的权。
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
典例解析
典例解析
解:选手A的最后得分是
选手B的最后得分是
由上可知选手B获得第一名,选手A获得第二名。
选手 演讲内容 演讲能力 演讲效果
A 85 95 95
B 95 85 95
1.某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是
(A)84 (B) 86 (C) 88 (D) 90
( D )
2.若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是
A:(x+y)/2 B:(x+y)/(m+n)
C:(mx+ny)/(x+y) D:(mx+ny)/(m+n)
( D )
达标检测
3.已知数据a1,a2,a3的平均数是a,那么数据2a1+1,2a2+1,2a3+1 的平均数是
(A) a (B)2a (C) 2a+1 (D) 2a/3+1
4.一组6个数1,2,3,x, y, z 的平均数是 4
(1)求x, y, z 三数的平均数;
解:由题意可得(1+2+3+x+y+z)/6=4
即 1+2+3+x+y+z=24 ,所以 x+y+z=18
所以 (x+y+z)/3=18/3=6
( C )
(2)求 4x+5, 4y+6, 4z+7 的平均数.
达标检测
D
5.已知:x1,x2,x3… x10的平均数是a, x11,x12,x13… x30的平均数是b,则x1,x2,x3… x30的平均数是( )
(A) (a+b) (B) (a+b)
(C) (10a+30b)
(D) (10a+20b)
(1)则数据x1+3,x2 +3 … xn +3的平均数________.
(2)则数据10x1,10x2 … 10xn 的平均数________.
a+3
10a
6.若x1,x2.......xn的平均数是a
达标检测
考试 平时1 平时2 平时3 期中 期末
成绩 89 78 85 90 87
7.小明同学在初二年级第一学期的数学成绩如下表格, 请按图示的平时、期中、期末的权重, 计算小明同学的学期总评成绩.
期中
30%
期末
60%
平时
10%
解:
先计算小明的平时成绩:
(89+78+85)÷3
= 84
再计算小明的总评成绩:
84×10%+ 90×30%+ 87×60%
= 87.6 (分)
达标检测
8.某公司对应聘者A、B、C、D进行面试时, 按三个方面给予打分如右表.你就公司主事身份探索下列问题:
⑴总分计算发现D最高, 故录用D.
这样的录用中,三个方面的权重各是多少
合理吗
项 目 占分 A B C D
专业知识 20 14 18 17 16
工作经验 20 18 16 14 16
仪表形象 20 12 11 14 14
⑵若设置上述三个方面的重要性之比为6:3:1, 那么这三个方面的权重分别是_________________, 该录用谁
60%
, 30%
, 10%
⑶若设置上述三个方面的重要性之比为10:7:3, 那么这三个方面的权重分别是_________________, 又该录用谁
50%
, 35%
, 15%
达标检测
33.33%
, 33.33%
, 33.33%
不合理,仪表形象没有专业知识和工作经验重要
B
B
1. 你能说说算术平均数与加权平均数的区别 和联系吗?
(2) 在实际问题中,各项权不相等时,计算平均数时就要采用加权平均数,当各项权相等时,计算平均数就要采用算术平均数.
(1) 算术平均数是加权平均数的一种特殊情况(它特殊在各项的权相等)
2. 加权平均数中“权”有几种表现形式?
(1) 整数的形式;
(2) 比的形式;
(3) 百分比的形式;
小结梳理
