四川省绵阳市2013届高三第二次诊断性考试数学(文)试题
文档属性
| 名称 | 四川省绵阳市2013届高三第二次诊断性考试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 166.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-29 10:17:11 | ||
图片预览



文档简介
四川省绵阳市2013届高三二诊模拟试题
文科数学(第一卷)
一、选择题:只有唯一正确答案,每小题5分,共50分
1、集合,,则集合为 ( )
(A) (B) (C) (D)
2、复数的虚部是( )
(A) (B) (C) (D)
3、已知,则的值为( )
(A) (B) (C) (D)
4、阅读右边的程序框图,运行相应的程序,则输出S的值为( )
(A)8 (B)18 (C)26 (D)80
5、设、b是两条不同的直线,、是两个不同的平面,则下列四个命题中正确的是( )
(A)若⊥b,⊥,则b∥ (B)若∥,⊥,则⊥
(C)若⊥,⊥,则 ∥ (D)若⊥b,⊥,b⊥,则⊥
6、函数的部分图象如图所示,则此函数的解析式为( )
(A) (B)
(C) (D)
7、对一切实数x,不等式恒成立,则实数a的取值范围是( )
(A) (B) (C) (D)
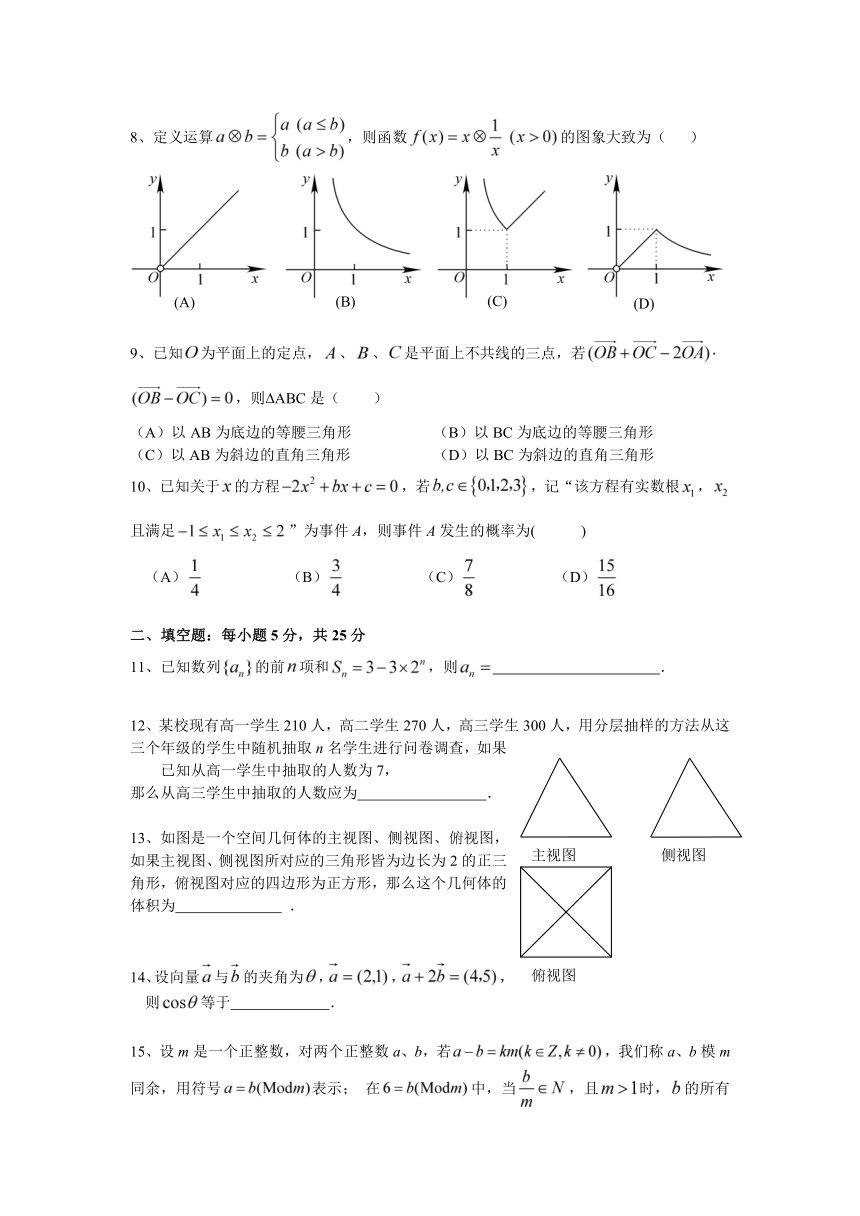
8、定义运算,则函数的图象大致为( )
9、已知为平面上的定点,、、是平面上不共线的三点,若
,则(ABC是( )
(A)以AB为底边的等腰三角形 (B)以BC为底边的等腰三角形
(C)以AB为斜边的直角三角形 (D)以BC为斜边的直角三角形
10、已知关于的方程,若,记“该方程有实数根,且满足”为事件A,则事件A发生的概率为( )
(A) (B) (C) (D)
二、填空题:每小题5分,共25分
11、已知数列的前项和,则 .
12、某校现有高一学生210人,高二学生270人,高三学生300人,用分层抽样的方法从这
三个年级的学生中随机抽取n名学生进行问卷调查,如果已知从高一学生中抽取的人数为7,
那么从高三学生中抽取的人数应为 .
13、如图是一个空间几何体的主视图、侧视图、俯视图,如果主视图、侧视图所对应的三角形皆为边长为2的正三角形,俯视图对应的四边形为正方形,那么这个几何体的体积为 .
14、设向量与的夹角为,,,则等于 .
15、设m是一个正整数,对两个正整数a、b,若,我们称a、b模m同余,用符号表示; 在中,当,且时,的所有可取值为 .
文科数学(第二卷)
三、解答题:总分75分
16、(本题满分12分)已知的面积满足,的
夹角为.
(Ⅰ)求的取值范围;
(Ⅱ)求函数的最大值.
17、(本题满分12分)三棱锥中,,,.
(Ⅰ)求证:平面平面;
(Ⅱ)当时,求三棱锥的体积.
18、(本题满分12分)
设函数满足:对任意的实数有
(Ⅰ)求的解析式;
(Ⅱ)若方程有解,求实数的取值范围.
19、(本题满分12分)已知某公司生产某品牌服装的年固定成本为10万元,每生产一千件,需要另投入2.7万元.设该公司年内共生产该品牌服装千件并全部销售完,每千件的销售收入为万元,且.
(I)写出年利润(万元)关于年产量(千件)的函数关系式;
(Ⅱ)年生产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
20、(本题满分13分)
设数列为单调递增的等差数列,,且依次成等比数列.
(Ⅰ)求数列的通项公式;
(Ⅱ)若,求数列的前项和;
(Ⅲ)若,求数列的前项和.
21.(本小题满分14分)已知函数()的图象为曲线.
(Ⅰ)求曲线上任意一点处的切线的斜率的取值范围;
(Ⅱ)若曲线上存在两点处的切线互相垂直,求其中一条切线与曲线的切点的横坐标的取值范围;
(Ⅲ)试问:是否存在一条直线与曲线C同时切于两个不同点?如果存在,求出符合条件的所有直线方程;若不存在,说明理由.
四川省绵阳市2013届高三二诊模拟试题
文科数学参考答案
一、选择题:1、B 2、C 3、A 4、C 5、D 6、A 7、B 8、D 9、B 10、C
二、填空题:11、() 12、10 13、 14、 15、2,3,4
三、解答题:
16、解:(I)由题意知 …………1分
(II)
…………9分
17、证明:(Ⅰ)作平面于点,∵,
∴,即为的外心
又∵中,
故为边的中点
所以平面
即证:平面平面. .......6分
(Ⅱ)∵,,∴为正三角形
∵ , ∴
∴
∴三棱锥的体积
.………….12分
18、解:⑴
所以 …………………5分
⑵①当时,不成立.
②当时,令则
因为函数在上单增,所以
③当时,令则
因为函数在上单增,所以
综上,实数的取值范围是 ……………………12分
19、解:(I)当时,;
当时,.
∴ 年利润(万元)关于年产量(千件)的函数关系式为
…………………6分
(Ⅱ)当时,由,
即年利润在上单增,在上单减
∴ 当时,取得最大值,且(万元).
当时,,仅当时取“=”
综上可知,当年产量为千件时,该公司在这一品牌服装的生产中所获年利润最大,最大值为万元. …………………12分
20、解:(Ⅰ)…….4分
(Ⅱ)∵
∴
相减,得
∴. …………………….13分
(Ⅲ)则………13分
21、解:(Ⅰ),则,
即曲线上任意一点处的切线的斜率的取值范围是;------------3分
(Ⅱ)由(1)可知,---------------------------------------------------------5分
解得或,由或
得:;-------------------------------7分
(Ⅲ)设存在过点A的切线曲线C同时切于两点,另一切点为B,
,
则切线方程是:,
化简得:,
而过B的切线方程是,
由于两切线是同一直线,
则有:,得,----------------------11分
又由,
即
,即
即,
得,但当时,由得,这与矛盾。
所以不存在一条直线与曲线C同时切于两点. --------------------------------14分
文科数学(第一卷)
一、选择题:只有唯一正确答案,每小题5分,共50分
1、集合,,则集合为 ( )
(A) (B) (C) (D)
2、复数的虚部是( )
(A) (B) (C) (D)
3、已知,则的值为( )
(A) (B) (C) (D)
4、阅读右边的程序框图,运行相应的程序,则输出S的值为( )
(A)8 (B)18 (C)26 (D)80
5、设、b是两条不同的直线,、是两个不同的平面,则下列四个命题中正确的是( )
(A)若⊥b,⊥,则b∥ (B)若∥,⊥,则⊥
(C)若⊥,⊥,则 ∥ (D)若⊥b,⊥,b⊥,则⊥
6、函数的部分图象如图所示,则此函数的解析式为( )
(A) (B)
(C) (D)
7、对一切实数x,不等式恒成立,则实数a的取值范围是( )
(A) (B) (C) (D)
8、定义运算,则函数的图象大致为( )
9、已知为平面上的定点,、、是平面上不共线的三点,若
,则(ABC是( )
(A)以AB为底边的等腰三角形 (B)以BC为底边的等腰三角形
(C)以AB为斜边的直角三角形 (D)以BC为斜边的直角三角形
10、已知关于的方程,若,记“该方程有实数根,且满足”为事件A,则事件A发生的概率为( )
(A) (B) (C) (D)
二、填空题:每小题5分,共25分
11、已知数列的前项和,则 .
12、某校现有高一学生210人,高二学生270人,高三学生300人,用分层抽样的方法从这
三个年级的学生中随机抽取n名学生进行问卷调查,如果已知从高一学生中抽取的人数为7,
那么从高三学生中抽取的人数应为 .
13、如图是一个空间几何体的主视图、侧视图、俯视图,如果主视图、侧视图所对应的三角形皆为边长为2的正三角形,俯视图对应的四边形为正方形,那么这个几何体的体积为 .
14、设向量与的夹角为,,,则等于 .
15、设m是一个正整数,对两个正整数a、b,若,我们称a、b模m同余,用符号表示; 在中,当,且时,的所有可取值为 .
文科数学(第二卷)
三、解答题:总分75分
16、(本题满分12分)已知的面积满足,的
夹角为.
(Ⅰ)求的取值范围;
(Ⅱ)求函数的最大值.
17、(本题满分12分)三棱锥中,,,.
(Ⅰ)求证:平面平面;
(Ⅱ)当时,求三棱锥的体积.
18、(本题满分12分)
设函数满足:对任意的实数有
(Ⅰ)求的解析式;
(Ⅱ)若方程有解,求实数的取值范围.
19、(本题满分12分)已知某公司生产某品牌服装的年固定成本为10万元,每生产一千件,需要另投入2.7万元.设该公司年内共生产该品牌服装千件并全部销售完,每千件的销售收入为万元,且.
(I)写出年利润(万元)关于年产量(千件)的函数关系式;
(Ⅱ)年生产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
20、(本题满分13分)
设数列为单调递增的等差数列,,且依次成等比数列.
(Ⅰ)求数列的通项公式;
(Ⅱ)若,求数列的前项和;
(Ⅲ)若,求数列的前项和.
21.(本小题满分14分)已知函数()的图象为曲线.
(Ⅰ)求曲线上任意一点处的切线的斜率的取值范围;
(Ⅱ)若曲线上存在两点处的切线互相垂直,求其中一条切线与曲线的切点的横坐标的取值范围;
(Ⅲ)试问:是否存在一条直线与曲线C同时切于两个不同点?如果存在,求出符合条件的所有直线方程;若不存在,说明理由.
四川省绵阳市2013届高三二诊模拟试题
文科数学参考答案
一、选择题:1、B 2、C 3、A 4、C 5、D 6、A 7、B 8、D 9、B 10、C
二、填空题:11、() 12、10 13、 14、 15、2,3,4
三、解答题:
16、解:(I)由题意知 …………1分
(II)
…………9分
17、证明:(Ⅰ)作平面于点,∵,
∴,即为的外心
又∵中,
故为边的中点
所以平面
即证:平面平面. .......6分
(Ⅱ)∵,,∴为正三角形
∵ , ∴
∴
∴三棱锥的体积
.………….12分
18、解:⑴
所以 …………………5分
⑵①当时,不成立.
②当时,令则
因为函数在上单增,所以
③当时,令则
因为函数在上单增,所以
综上,实数的取值范围是 ……………………12分
19、解:(I)当时,;
当时,.
∴ 年利润(万元)关于年产量(千件)的函数关系式为
…………………6分
(Ⅱ)当时,由,
即年利润在上单增,在上单减
∴ 当时,取得最大值,且(万元).
当时,,仅当时取“=”
综上可知,当年产量为千件时,该公司在这一品牌服装的生产中所获年利润最大,最大值为万元. …………………12分
20、解:(Ⅰ)…….4分
(Ⅱ)∵
∴
相减,得
∴. …………………….13分
(Ⅲ)则………13分
21、解:(Ⅰ),则,
即曲线上任意一点处的切线的斜率的取值范围是;------------3分
(Ⅱ)由(1)可知,---------------------------------------------------------5分
解得或,由或
得:;-------------------------------7分
(Ⅲ)设存在过点A的切线曲线C同时切于两点,另一切点为B,
,
则切线方程是:,
化简得:,
而过B的切线方程是,
由于两切线是同一直线,
则有:,得,----------------------11分
又由,
即
,即
即,
得,但当时,由得,这与矛盾。
所以不存在一条直线与曲线C同时切于两点. --------------------------------14分
同课章节目录
