河南省郑州市盛同学校2013届高三上学期期末考试数学(文)试题
文档属性
| 名称 | 河南省郑州市盛同学校2013届高三上学期期末考试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 389.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-29 11:38:48 | ||
图片预览




文档简介
盛同学校2013届高三上学期期末考试数学(文)试题
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.考试时间120分钟,满分150分.考生应首先阅读答题卡上的文宇信息,然后在答题卡上作答,在试题卷上作答无效.
第I卷
—、选择题 (毎小题5分,共60分)
1、已知集合,,,则集合P为
A. B.
C. D.
2、已知复数,则的虚部为
A、 B、 C、1 D、
3、“”是“”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4、已知直线,平面,且,,下列四个命题中是:
A、若∥,则; B、若,则∥;
C、若,则∥; D、若,则.
5、已知向量=(2,1),=(-1,),(2-)=0,则=
A. -12 B. -6 C. 6 D. 12
6、设是周期为2的奇函数,当时,,则
A. B. C. D.
7. 设a、b是两条不同的直线,是两个不同的平面,则下列四个命题: ①若,则 ②若,则I ③若,则或< ④若,,则.
其中正确命题的个数为
A. 1 B. 2 C. 3 D.4
8. 要得到函数的图象,只需将函数的图象沿x轴
A.向右平移个单位 B.向左平移个单位
C.向右平移个单位 D.向左平移个单位
9. 设函数则的值为
A. 15 B. 16
C. -5 D. -15
10. 右面的程序框图给出了计算数列的前8项和S的箅法,算法执行完毕后,输出的S为.
A. 8
B. 63
C. 92
D. 129
11.把一段长16米的铁丝截成两段,分别围成正方形,则两个正方形面积之和的最小值为 A.4 B.8
C.16 D. 32
12.设双曲线的两条渐近线与直线围成的三角形区域(包含边界)为P(x,y)为D内的一个动点,则目标函数的最小值为
A. —2 B. C.O D.
第Ⅱ卷 (非选择题 ,共 90 分)
二、填空题(本大题共4个小题,每小题5分,共20分,把答案填在答题卡的横线上)
13.若f(x)是幂函数,且满足=3,则f=______.
14.设等比数列{an}的公比q=(,前n项和为Sn,则=________.
15.设0A.(a-b)2 B.(a+b)2 C.a2b2 D.a2
16.设m为实数,若?{(x,y)|x2+y2≤25},则m的取值范围是________.
三、解答翅(共70分)
17.(本题满分12分)已知函数在区间 上的
最大值为2.
(1)求常数的值;
(2)在中,角,,所对的边是,,,若,,
面积为. 求边长.
18. (本题满分12分)汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆);
轿车A
轿车B
轿车C
舒适型
100
150
z
标准型
300
450
600
按类型用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆. (Ⅰ)求z的值; (Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率; (Ⅲ)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
19.(本小题满分12分)
某大学高等数学老师这学期分别用两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
(1)依茎叶图判断哪个班的平均分高?
(2)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率;
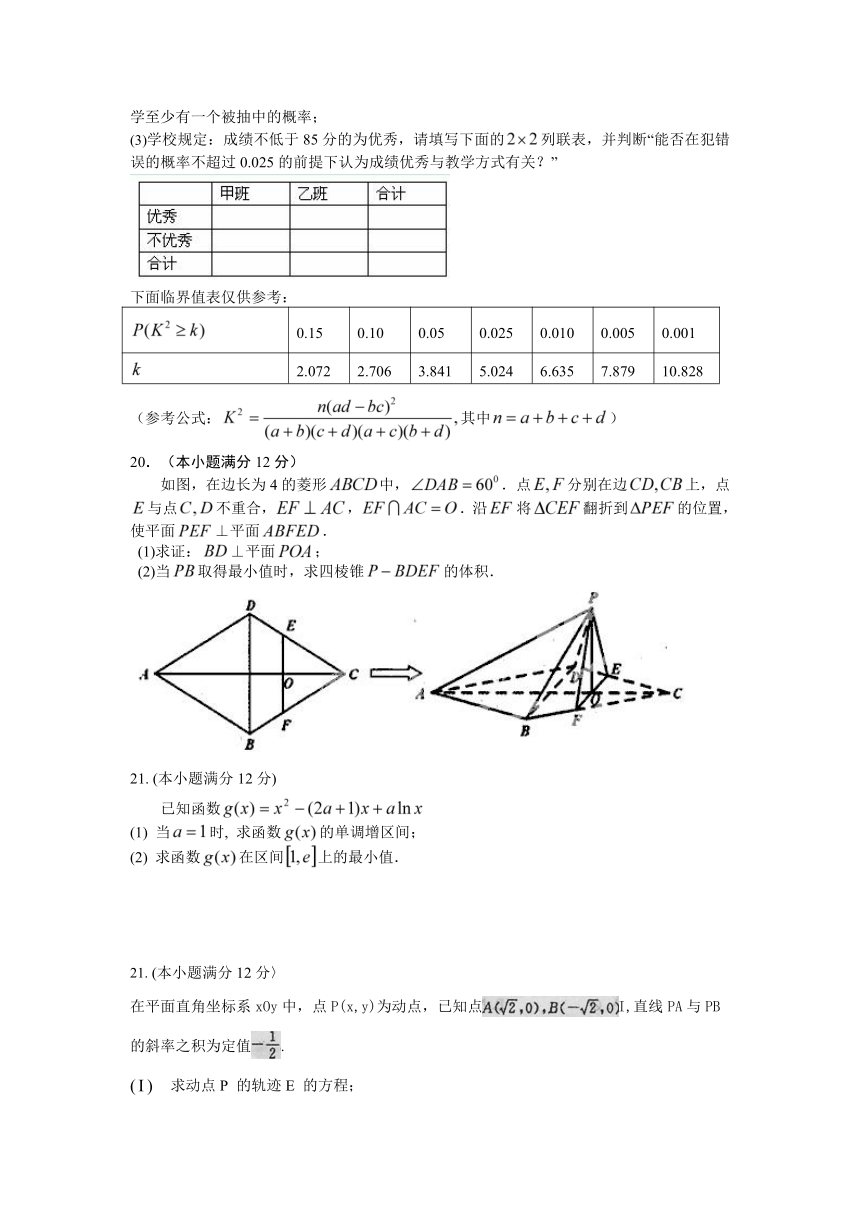
(3)学校规定:成绩不低于85分的为优秀,请填写下面的列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
下面临界值表仅供参考:
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:其中)
20.(本小题满分12分)
如图,在边长为4的菱形中,.点分别在边上,点与点不重合,,.沿将翻折到的位置,使平面⊥平面.
(1)求证:⊥平面;
(2)当取得最小值时,求四棱锥的体积.
21. (本小题满分12分)
已知函数
(1) 当时, 求函数的单调增区间;
(2) 求函数在区间上的最小值.
21. (本小题满分12分〉
在平面直角坐标系xOy中,点P(x,y)为动点,已知点I,直线PA与PB的斜率之积为定值.
(I) 求动点P的轨迹E的方程;
(II)若F(1,0),过点F的直线l交轨迹E于M、N两点,以MN为对角线的正方形的第三个顶点恰在y轴上,求直线l的方程.
22(10分明选讲
如图, 是△的外接圆,D是的中点,BD交AC于E.(1)求证:;
(2)若,O到AC的距离为1,求⊙O的半径.
文科数学 参考答案
选择题
1-12 BCAA DA DBACBB
二、填空题
13._1/3_____. 14.__63______. 15.__a+b)2____. 16.____0≤m≤____.
三、解答题
17. 解:(1)
∵ ∴
∵ 函数在区间 上是增函数,在区间 上是减函数
∴当即时,函数在区间上取到最大值.
此时,得
18. (1)设该厂本月生产轿车为n辆,由题意得, n/50=10/(100+300),所以n=2000. z=2000-100-300-150-450-600=400 (3)样本的平均数为9 , 那么与样本平均数之差的绝对值不超过0.5的数为9.4, 8.6, 9.2, 8.7, 9.3, 9.0这6个数,总的个数为8,所以该数与样本平均数之差的绝对值不超过0.5的概率为0.75
19、
“从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学”的一切可能结果组成的基本事件有:
一共15个,
“抽到至少有一个86分的同学”所组成的基本事件有:共9个,---------5分
故------------------------------------------------------7分
(Ⅲ)
--------------------------9分
,因此在犯错误的概率不超过0.025的前提下可以认为成绩优秀与教学方式有关.-----------------------12分
20、(Ⅰ)证明:
∵ 菱形的对角线互相垂直,
∴,∴, 1分
∵ ,∴.
∵ 平面⊥平面,平面平面,
且平面,
∴ 平面, ∵ 平面,∴ . 3分
∵ ,∴ 平面. 4分
(Ⅱ)如图,以为原点,建立空间直角坐标系. 5分
(ⅰ)设 因为,所以为等边三角形,
故,.又设,则,.
所以,,,
故 , 6分
所以,
当时,. 此时, 7分
由(Ⅰ)知,平面
所以. 8分
(ⅱ)设点的坐标为,
由(i)知,,则,,,.
所以,, 9分
∵,
∴.
∴,
∴. 10分
取,解得:, 所以. 11分
设直线与平面所成的角,
∴
. 12分
又∵∴. 13分
∵,∴.
因此直线与平面所成的角大于,即结论成立. 14分
21、(Ⅰ)当时,,
或。函数的单调增区间为……………… 3分
(Ⅱ) ,
当,单调增。
当,单调减. 单调增。
当,单调减, ………………………………………… 8分
(Ⅲ)令,
, 即
, ……………………………………… 12分
22题满分10分)选修4—1:几何证明选讲
解:(I)证明:∵,
∴,又,
∴△~△,∴,
∴CD=DE·DB; ………………(5分)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.考试时间120分钟,满分150分.考生应首先阅读答题卡上的文宇信息,然后在答题卡上作答,在试题卷上作答无效.
第I卷
—、选择题 (毎小题5分,共60分)
1、已知集合,,,则集合P为
A. B.
C. D.
2、已知复数,则的虚部为
A、 B、 C、1 D、
3、“”是“”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4、已知直线,平面,且,,下列四个命题中是:
A、若∥,则; B、若,则∥;
C、若,则∥; D、若,则.
5、已知向量=(2,1),=(-1,),(2-)=0,则=
A. -12 B. -6 C. 6 D. 12
6、设是周期为2的奇函数,当时,,则
A. B. C. D.
7. 设a、b是两条不同的直线,是两个不同的平面,则下列四个命题: ①若,则 ②若,则I ③若,则或< ④若,,则.
其中正确命题的个数为
A. 1 B. 2 C. 3 D.4
8. 要得到函数的图象,只需将函数的图象沿x轴
A.向右平移个单位 B.向左平移个单位
C.向右平移个单位 D.向左平移个单位
9. 设函数则的值为
A. 15 B. 16
C. -5 D. -15
10. 右面的程序框图给出了计算数列的前8项和S的箅法,算法执行完毕后,输出的S为.
A. 8
B. 63
C. 92
D. 129
11.把一段长16米的铁丝截成两段,分别围成正方形,则两个正方形面积之和的最小值为 A.4 B.8
C.16 D. 32
12.设双曲线的两条渐近线与直线围成的三角形区域(包含边界)为P(x,y)为D内的一个动点,则目标函数的最小值为
A. —2 B. C.O D.
第Ⅱ卷 (非选择题 ,共 90 分)
二、填空题(本大题共4个小题,每小题5分,共20分,把答案填在答题卡的横线上)
13.若f(x)是幂函数,且满足=3,则f=______.
14.设等比数列{an}的公比q=(,前n项和为Sn,则=________.
15.设0
16.设m为实数,若?{(x,y)|x2+y2≤25},则m的取值范围是________.
三、解答翅(共70分)
17.(本题满分12分)已知函数在区间 上的
最大值为2.
(1)求常数的值;
(2)在中,角,,所对的边是,,,若,,
面积为. 求边长.
18. (本题满分12分)汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆);
轿车A
轿车B
轿车C
舒适型
100
150
z
标准型
300
450
600
按类型用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆. (Ⅰ)求z的值; (Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率; (Ⅲ)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
19.(本小题满分12分)
某大学高等数学老师这学期分别用两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
(1)依茎叶图判断哪个班的平均分高?
(2)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率;
(3)学校规定:成绩不低于85分的为优秀,请填写下面的列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
下面临界值表仅供参考:
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:其中)
20.(本小题满分12分)
如图,在边长为4的菱形中,.点分别在边上,点与点不重合,,.沿将翻折到的位置,使平面⊥平面.
(1)求证:⊥平面;
(2)当取得最小值时,求四棱锥的体积.
21. (本小题满分12分)
已知函数
(1) 当时, 求函数的单调增区间;
(2) 求函数在区间上的最小值.
21. (本小题满分12分〉
在平面直角坐标系xOy中,点P(x,y)为动点,已知点I,直线PA与PB的斜率之积为定值.
(I) 求动点P的轨迹E的方程;
(II)若F(1,0),过点F的直线l交轨迹E于M、N两点,以MN为对角线的正方形的第三个顶点恰在y轴上,求直线l的方程.
22(10分明选讲
如图, 是△的外接圆,D是的中点,BD交AC于E.(1)求证:;
(2)若,O到AC的距离为1,求⊙O的半径.
文科数学 参考答案
选择题
1-12 BCAA DA DBACBB
二、填空题
13._1/3_____. 14.__63______. 15.__a+b)2____. 16.____0≤m≤____.
三、解答题
17. 解:(1)
∵ ∴
∵ 函数在区间 上是增函数,在区间 上是减函数
∴当即时,函数在区间上取到最大值.
此时,得
18. (1)设该厂本月生产轿车为n辆,由题意得, n/50=10/(100+300),所以n=2000. z=2000-100-300-150-450-600=400 (3)样本的平均数为9 , 那么与样本平均数之差的绝对值不超过0.5的数为9.4, 8.6, 9.2, 8.7, 9.3, 9.0这6个数,总的个数为8,所以该数与样本平均数之差的绝对值不超过0.5的概率为0.75
19、
“从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学”的一切可能结果组成的基本事件有:
一共15个,
“抽到至少有一个86分的同学”所组成的基本事件有:共9个,---------5分
故------------------------------------------------------7分
(Ⅲ)
--------------------------9分
,因此在犯错误的概率不超过0.025的前提下可以认为成绩优秀与教学方式有关.-----------------------12分
20、(Ⅰ)证明:
∵ 菱形的对角线互相垂直,
∴,∴, 1分
∵ ,∴.
∵ 平面⊥平面,平面平面,
且平面,
∴ 平面, ∵ 平面,∴ . 3分
∵ ,∴ 平面. 4分
(Ⅱ)如图,以为原点,建立空间直角坐标系. 5分
(ⅰ)设 因为,所以为等边三角形,
故,.又设,则,.
所以,,,
故 , 6分
所以,
当时,. 此时, 7分
由(Ⅰ)知,平面
所以. 8分
(ⅱ)设点的坐标为,
由(i)知,,则,,,.
所以,, 9分
∵,
∴.
∴,
∴. 10分
取,解得:, 所以. 11分
设直线与平面所成的角,
∴
. 12分
又∵∴. 13分
∵,∴.
因此直线与平面所成的角大于,即结论成立. 14分
21、(Ⅰ)当时,,
或。函数的单调增区间为……………… 3分
(Ⅱ) ,
当,单调增。
当,单调减. 单调增。
当,单调减, ………………………………………… 8分
(Ⅲ)令,
, 即
, ……………………………………… 12分
22题满分10分)选修4—1:几何证明选讲
解:(I)证明:∵,
∴,又,
∴△~△,∴,
∴CD=DE·DB; ………………(5分)
同课章节目录
