第三章 图形的平移与旋转 单元检测卷02(含解析)
文档属性
| 名称 | 第三章 图形的平移与旋转 单元检测卷02(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 07:59:31 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第三章《图形的平移与旋转》检测卷02
第I卷(选择题)
选择题(本大题共10小题,每小题3分,共30分)
1.在平面直角坐标系中,点关于原点对称点在()
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.下列各徽标中,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
3.已知点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,则( )
A.x=﹣1,y=2 B.x=﹣1,y=8 C.x=﹣1,y=﹣2 D.x=1,y=8
4.如图,沿射线方向平移到(点E在线段上),如果,,那么平移距离为(???????)
A.3cm B.5cm C.8cm D.13cm
5.如图,在中,,将绕点逆时针旋转到的位置,使得,则的度数是(???????)
A. B. C. D.
6.下列四个图形中,中心对称图形是(???????)
A. B. C. D.
7.如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一直线上,则三角板ABC旋转的度数是(??????? ).
A.60° B.90° C.120° D.150°
8.京剧脸谱、剪纸等图案一般蕴含着对称美,下列选取的图片中既是轴对称图形,又是中心对称图形的是(???????)
A. B. C. D.
9.下列图形中既是轴对称图形,也是中心对称图形的是(?????)
A. B. C. D.
10.如图,在平面直角坐标系中,线段的两个端点是,.将线段沿某一方向平移后,若点的对应点的坐标为,则点的对应点的坐标为(???????)
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共7小题,每小题4分,共28分)
11.如图,将正方形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点A,B,C的坐标分别为,,.是关于轴的对称图形,将绕点逆时针旋转180°,点的对应点为M,则点M的坐标为________.
12.如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE=_______.
13.如图,三角形中,,D是BC上一点,三角形逆时针旋转后到达三角形的位置.
(1)旋转中心是_________;
(2)旋转了_________度.
14.如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为_____.
15.如图,已知∠1=75°,将直线m平行移动到直线n的位置,则∠2﹣∠3=_____°.
16.如图,某住宅小区内有一长方形地,若在长方形地内修筑同样宽的小路(图中阴影都分),余下部分绿化,小路的宽均为2m,则绿化的面积为____.
17.若点和关于原点对称,则的值是___________.
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.画图并填空:
如图,在128 的方格纸中,每个小正方形的边长都为1 ,△ABC 的顶点都在方格纸的格点上,将△ABC 按照某方向经过一次平移后得到△A' B'C ' ,图中标出了点C 的对应点C ' .
(1)请画出△A' B'C ' ;
(2)利用方格纸,在△ABC 中画出AC 边上的中线BD 和BC 边上的高AE ;
(3)点F 为方格纸上的格点(异于点B ),若S ACB S ACF ,则图中格点F 共有 个.(请在方格纸中标出点F )
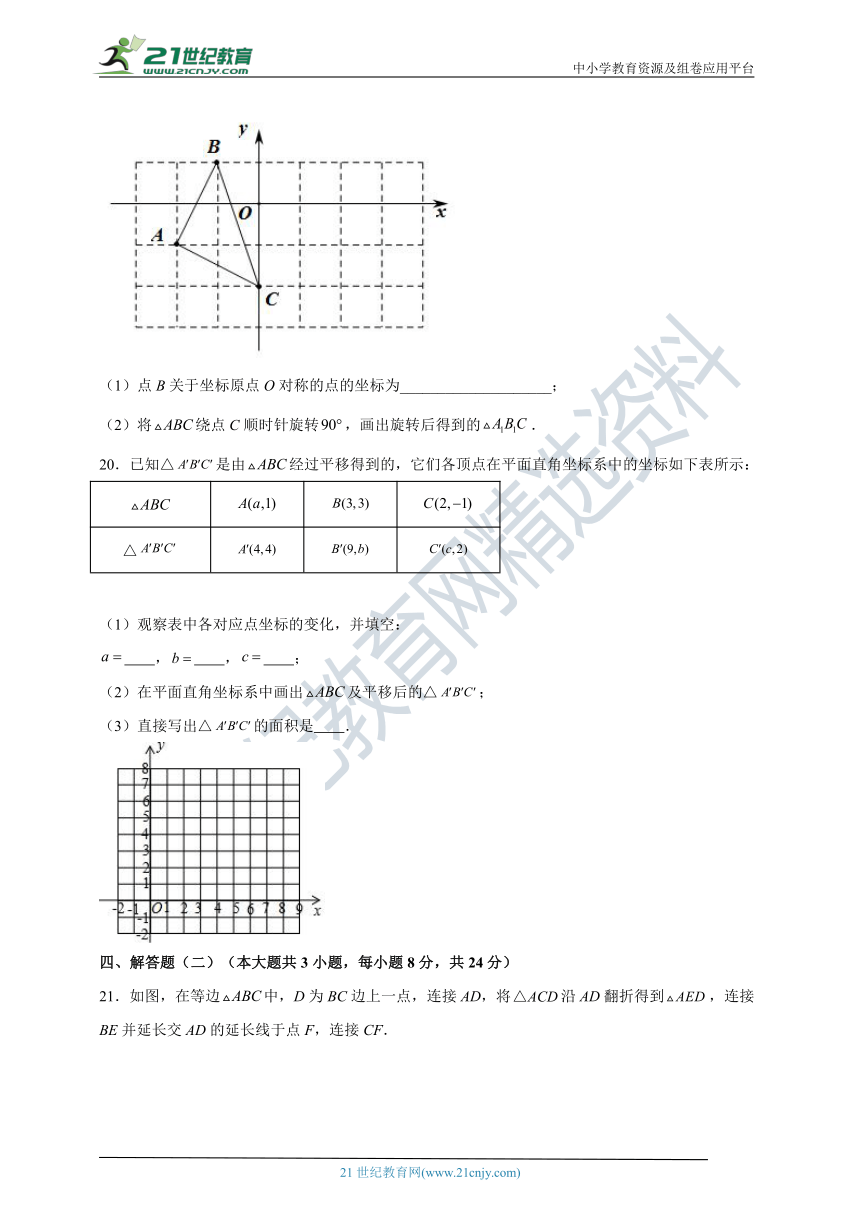
19.如图,在平面直角坐标系中,的三个顶点坐标分别为、、.
(1)点B关于坐标原点O对称的点的坐标为____________________;
(2)将绕点C顺时针旋转,画出旋转后得到的.
20.已知△是由经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△
(1)观察表中各对应点坐标的变化,并填空:
, , ;
(2)在平面直角坐标系中画出及平移后的△;
(3)直接写出△的面积是 .
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.如图,在等边中,D为BC边上一点,连接AD,将沿AD翻折得到,连接BE并延长交AD的延长线于点F,连接CF.
(1)若,求的度数;
(2)若,求的大小;
(3)猜想CF,BF,AF之间的数量关系,并证明.
22.如图网格中,的顶点均在格点上,点、的坐标分别是、.
(1)点A关于点中心对称点的坐标为(_______,_______);
(2)绕点顺时针旋转后得到,在方格纸中画出,并写出点的坐标(______,_______);
(3)在轴上找一点,使得最小,请在图中标出点的位置,并求出这个最小值.
23.如图所示,、点在轴上,将三角形沿轴负方向平移,平移后的图形为三角形,且点的坐标为,且.
(1)直接写出点的坐标 ;
(2)直接写出点的坐标 ;
五、解答题(三)(本大题共2小题,每小题10分,共20分)
24.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;并写出点A2、B2、C2坐标;
(3)请画出△ABC绕O逆时针旋转90°后的△A3B3C3;并写出点A3、B3、C3坐标.
25.如图所示,每个小正方形的边长为1个单位长度,的顶点均在格点上,点、的坐标分别是、.
(1)点关于点中心对称的点的坐标为 ;
(2)绕点顺时针旋转后得到△,在图中画出△,并写出点的坐标: .
第三章《图形的平移与旋转》检测卷02
第I卷(选择题)
选择题(本大题共10小题,每小题3分,共30分)
1.在平面直角坐标系中,点关于原点对称点在()
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D
【解析】
【分析】
先依据,即可得出点P所在的象限,再根据两个点关于原点对称时,它们的坐标符号相反,即可得出结论.
【详解】
解:∵,∴点在第二象限,
∴点关于原点对称点在第四象限.
故选D.
【点睛】
本题主要考查了关于原点对称的两个点的坐标特征,明确关于原点对称的两个点的横、纵坐标均互为相反数是解答的关键.
2.下列各徽标中,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
【答案】C
【解析】
【分析】
根据轴对称图形的定义和中心对称图形的定义,分别进行判断,即可得到答案.
【详解】
解:A、不是轴对称图形,也不是中心对称图形,故A错误;
B、是轴对称图形,也是中心对称图形,故B错误;
C、是轴对称图形,但不是中心对称图形,故C正确;
D、不是轴对称图形,也不是中心对称图形,故D错误;
故选:C.
【点睛】
本题考查了轴对称图形和中心对称图形的识别,解题的关键是熟记定义.
3.已知点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,则( )
A.x=﹣1,y=2 B.x=﹣1,y=8 C.x=﹣1,y=﹣2 D.x=1,y=8
【答案】A
【解析】
【分析】
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点是P′(﹣x,﹣y).直接利用关于原点对称点的性质得出x,y的值进而得出答案.
【详解】
解:∵点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,
∴x﹣2+x+4=0,y﹣5=﹣3,
解得:x=﹣1,y=2,
故选:A.
【点睛】
此题主要考查了关于原点对称点的性质,正确把握横纵坐标的关系是解题关键.
4.如图,沿射线方向平移到(点E在线段上),如果,,那么平移距离为(???????)
A.3cm B.5cm C.8cm D.13cm
【答案】A
【解析】
【分析】
观察图象,发现平移前后,B、E对应,C、F对应,根据平移的性质,易得平移的距离=BE,进而可得答案.
【详解】
解:根据平移的性质,
易得平移的距离=BE=8-5=3cm,
故选:A.
【点睛】
本题考查平移的性质,经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等,本题关键要找到平移的对应点.
5.如图,在中,,将绕点逆时针旋转到的位置,使得,则的度数是(???????)
A. B. C. D.
【答案】C
【解析】
【分析】
根据旋转的性质得AC′=AC,∠B′AB=∠C′AC,再根据等腰三角形的性质得∠AC′C=∠ACC′,然后根据平行线的性质由CC′∥AB得∠ACC′=∠CAB=70°,则∠AC′C=∠ACC′=70°,再根据三角形内角和计算出∠CAC′=40°,所以∠B′AB=40°.
【详解】
∵绕点逆时针旋转到的位置,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,
故选C.
【点睛】
本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了平行线的性质.
6.下列四个图形中,中心对称图形是(???????)
A. B. C. D.
【答案】D
【解析】
【分析】
根据中心对称图形的概念结合各图形的特点求解.
【详解】
解:A、不是中心对称图形,不符合题意;
B、不是中心对称图形,不符合题意;
C、不是中心对称图形,不符合题意;
D、是中心对称图形,符合题意.
故选:D.
【点睛】
本题考查了中心对称图形与轴对称图形的概念.判断中心对称图形是要寻找对称中心,图形旋转180度后与原图形重合.
7.如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一直线上,则三角板ABC旋转的度数是(??????? ).
A.60° B.90° C.120° D.150°
【答案】D
【解析】
【分析】
根据旋转角的定义,两对应边的夹角就是旋转角,即可求解.
【详解】
解: 旋转角是∠CAC′=180°﹣30°=150°.
故选D.
【点睛】
考点:旋转的性质.
8.京剧脸谱、剪纸等图案一般蕴含着对称美,下列选取的图片中既是轴对称图形,又是中心对称图形的是(???????)
A. B. C. D.
【答案】D
【解析】
【分析】
根据轴对称图形与中心对称图形的概念进行判断.
【详解】
解:A、是轴对称图形,不是中心对称图形,故本选项不合题意;
B、不是轴对称图形,也不是中心对称图形,故本选项不合题意;
C、不是轴对称图形,是中心对称图形,故本选项不合题意;
D、既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
【点睛】
本题考查了中心对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
9.下列图形中既是轴对称图形,也是中心对称图形的是(?????)
A. B. C. D.
【答案】B
【解析】
【分析】
根据轴对称图形与中心对称图形的概念求解.
【详解】
解:A、既不是轴对称图形,也不是中心对称图形,故此选项不符合题意;
B、既是轴对称图形,也是中心对称图形,故此选项符合题意;
C、是轴对称图形,不是中心对称图形,故此选项不符合题意;
D、不是轴对称图形,是中心对称图形,故此选项不符合题意.
故选:B.
【点睛】
此题主要考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
10.如图,在平面直角坐标系中,线段的两个端点是,.将线段沿某一方向平移后,若点的对应点的坐标为,则点的对应点的坐标为(???????)
A. B. C. D.
【答案】C
【解析】
【分析】
观察点到的变化特征:横坐标减小3,纵坐标减小3,根据图形平移的性质解题即可.
【详解】
平移后得到
横坐标减小3,纵坐标减小3,
即
故选:C.
【点睛】
本题考查坐标与图形、平移等知识,是重要考点,难度较易,掌握相关知识是解题关键.
第II卷(非选择题)
二、填空题(本大题共7小题,每小题4分,共28分)
11.如图,将正方形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点A,B,C的坐标分别为,,.是关于轴的对称图形,将绕点逆时针旋转180°,点的对应点为M,则点M的坐标为________.
【答案】
【解析】
【分析】
根据题意,画出旋转后图形,即可求解
【详解】
解:如图,将绕点逆时针旋转180°,所以点的对应点为M的坐标为.
故答案为:
【点睛】
本题考查平面直角坐标系内图形的对称,旋转,解题关键是理解对称旋转的含义,并结合网格解题.
12.如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE=_______.
【答案】3.
【解析】
【详解】
试题分析:∵将△ABC绕点A顺时针旋转60°得到△AED,∴∠BAE=60°,AB=AE,∴△BAE是等边三角形,∴BE=3.故答案为3.
考点:旋转的性质.
13.如图,三角形中,,D是BC上一点,三角形逆时针旋转后到达三角形的位置.
(1)旋转中心是_________;
(2)旋转了_________度.
【答案】???? 点A???? 60
【解析】
【分析】
根据等边三角形的性质得AB=AC,∠BAC=60°,然后根据旋转的求解.
【详解】
解:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵点△ABD经过旋转后到达△ACE的位置,
∴旋转中心是点A,∠BAC等于旋转角,即逆时针旋转了60度.
故答案为:点A、60.
【点睛】
本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
14.如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为_____.
【答案】
【解析】
【详解】
试题分析:∵在等边△ABC中,∠B=60°,AB=6,D是BC的中点,∴AD⊥BD,∠BAD=∠CAD=30°.
∴AD=ABcos30°=6×.
根据旋转的性质知,∠EAC=∠DAB=30°,AD=AE,
∴∠DAE=∠EAC+∠BAD=60°.∴△ADE的等边三角形.
∴DE=AD=,即线段DE的长度为.
15.如图,已知∠1=75°,将直线m平行移动到直线n的位置,则∠2﹣∠3=_____°.
【答案】105
【解析】
【分析】
直接利用平移的性质结合三角形外角的性质得出答案.
【详解】
解:如图,由题意可得:mn,
∴∠CAD+∠1=180°.
∵∠3=∠4,
∴∠4+∠CAD=∠2,
∴∠2﹣∠3=∠CAD+∠3﹣∠3=∠CAD=180°﹣∠1=180°﹣75°=105°.
故答案为:105.
【点睛】
本题考查了平移的性质、三角形外角的性质以及平行线的性质,正确转化角的关系是解题的关键.
16.如图,某住宅小区内有一长方形地,若在长方形地内修筑同样宽的小路(图中阴影都分),余下部分绿化,小路的宽均为2m,则绿化的面积为____.
【答案】540
【解析】
【分析】
利用平移把不规则的图形变为规则图形,如此一来,所有绿化面积之和就变为了(32-2)(20-2)m2,进而即可求出答案.
【详解】
利用平移可得,两条小路的总面积是:(32-2)(20-2)=540(m2).
故答案为540.
【点睛】
此题主要考查了生活中的平移现象,这类题目体现了数形结合的思想,需利用平移把不规则的图形变为规则图形,进而即可列出方程,求出答案.
17.若点和关于原点对称,则的值是___________.
【答案】-3.
【解析】
【分析】
先求出的值,然后相加即可.
【详解】
解:点和关于原点对称,
则a=-1,b=-2,
,
故答案为:-3.
【点睛】
本题考查了关于原点对称点的坐标变化规律,解题关键是熟知变化规律,准确进行计算.
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.画图并填空:
如图,在128 的方格纸中,每个小正方形的边长都为1 ,△ABC 的顶点都在方格纸的格点上,将△ABC 按照某方向经过一次平移后得到△A' B'C ' ,图中标出了点C 的对应点C ' .
(1)请画出△A' B'C ' ;
(2)利用方格纸,在△ABC 中画出AC 边上的中线BD 和BC 边上的高AE ;
(3)点F 为方格纸上的格点(异于点B ),若S ACB S ACF ,则图中格点F 共有 个.(请在方格纸中标出点F )
【答案】(1)见解析;(2)见解析;(3)5
【解析】
【分析】
(1)利用点C和C′的位置确定平移的方向与距离,然后利用此平移规律画出A、B的对应点即可;
(2)利用网格特点确定AC的中点D,从而得到中线BD;再利用网格特点过A点作BC的垂线,确定垂足E点;
(3)过B点作AC的平行线可确定2个格点F,把直线AC向右平移个单位,再向上平移1个单位得到3个格点F.
【详解】
解:(1)如图,△A'B'C'为所作;
(2)如图,BD、AE为所作;
(3)若S△ACB=S△ACF,则图中格点F共有5个,如图.
故答案为5.
【点睛】
本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
19.如图,在平面直角坐标系中,的三个顶点坐标分别为、、.
(1)点B关于坐标原点O对称的点的坐标为____________________;
(2)将绕点C顺时针旋转,画出旋转后得到的.
【答案】(1);(2)见解析
【解析】
【分析】
(1)根据关于原点对称的点的坐标特征写出B关于原点的对称点的坐标即可;
(2)利用网格特点和旋转的性质画出点A、B的对应点A1、B1,从而得到△A1B1C.
【详解】
解:(1)∵B(?1,1),
∴点B关于原点的对称点的坐标为(1,-1),
故答案为:(1,-1);
(2)如图,△A1B1C为所作;
【点睛】
本题考查了作图-旋转变换,关于原点对称的两个点的坐标特点,解决本题的关键是掌握旋转的性质.
20.已知△是由经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△
(1)观察表中各对应点坐标的变化,并填空:
, , ;
(2)在平面直角坐标系中画出及平移后的△;
(3)直接写出△的面积是 .
【答案】(1)-2,6,8;(2)见解析;(3)9
【解析】
【分析】
(1)观察表中各对应点坐标的变化,△是由△ABC经过向上平移3个单位,向右平移6个单位得到的,进而可填空;
(2)根据(1)即可在平面直角坐标系中画出△ABC及平移后的△;
(3)根据割补法即可求出△的面积.
【详解】
(1)观察表中点和点坐标的变化,点和点坐标的变化可知:
△是由经过向上平移3个单位,向右平移6个单位得到的,
,,;
故答案为:,6,8;
(2)如图,及△即为所求;
(3)△的面积为:.
故答案为:9.
【点睛】
本题考查了作图-平移变换,解决本题的关键是掌握平移的性质.
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.如图,在等边中,D为BC边上一点,连接AD,将沿AD翻折得到,连接BE并延长交AD的延长线于点F,连接CF.
(1)若,求的度数;
(2)若,求的大小;
(3)猜想CF,BF,AF之间的数量关系,并证明.
【答案】(1)20°;(2);(3)AF= CF+BF,理由见解析
【解析】
【分析】
(1)由△ABC是等边三角形,得到AB=AC,∠BAC=∠ABC=60°,由折叠的性质可知,∠EAD=∠CAD=20°,AC=AE,则∠BAE=∠BAC-∠EAD-∠CAD=20°,AB=AE,,∠CBF=∠ABE-∠ABC=20°;
(2)同(1)求解即可;
(3)如图所示,将△ABF绕点A逆时针旋转60°得到△ACG,先证明△AEF≌△ACF得到∠AFE=∠AFC,然后证明∠AFE=∠AFC=60°,得到∠BFC=120°,即可证明F、C、G三点共线,得到△AFG是等边三角形,则AF=GF=CF+CG=CF+BF.
【详解】
解:(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ABC=60°,
由折叠的性质可知,∠EAD=∠CAD=20°,AC=AE,
∴∠BAE=∠BAC-∠EAD-∠CAD=20°,AB=AE,
∴,
∴∠CBF=∠ABE-∠ABC=20°;
(2)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ABC=60°,
由折叠的性质可知,,AC=AE,
∴ ,AB=AE,
∴,
∴;
(3)AF= CF+BF,理由如下:
如图所示,将△ABF绕点A逆时针旋转60°得到△ACG,
∴AF=AG,∠FAG=60°,∠ACG=∠ABF,BF=CG
在△AEF和△ACF中,
,
∴△AEF≌△ACF(SAS),
∴∠AFE=∠AFC,
∵∠CBF+∠BCF+∠BFD+∠CFD=180°,∠CAF+∠CFA+∠ACD+∠CFD=180°,
∴∠BFD=∠ACD=60°,
∴∠AFE=∠AFC=60°,
∴∠BFC=120°,
∴∠BAC+∠BFC=180°,
∴∠ABF+∠ACF=180°,
∴∠ACG+∠ACF=180°,
∴F、C、G三点共线,
∴△AFG是等边三角形,
∴AF=GF=CF+CG=CF+BF.
【点睛】
本题主要考查了等边三角形的性质与判定,旋转的性质,折叠的性质,全等三角形的性质与判定,三角形内角和定理,熟知相关知识是解题的关键.
22.如图网格中,的顶点均在格点上,点、的坐标分别是、.
(1)点A关于点中心对称点的坐标为(_______,_______);
(2)绕点顺时针旋转后得到,在方格纸中画出,并写出点的坐标(______,_______);
(3)在轴上找一点,使得最小,请在图中标出点的位置,并求出这个最小值.
【答案】(1)-3,-2;(2)作图见解析;3,-1;(3)点P的位置见解析;.
【解析】
【分析】
(1)关于点中心对称点的特征是横纵坐标符号相反,可得点A关于点中心对称点的坐标;
(2)把点A、B顺时针旋转90°对应点分别为A1、B1,连结OA1、OB1、A1B1,可得,进而可得各点坐标;
(3)作点关于轴的对称点,连接交轴于点,由勾股定理可得.
【详解】
解:(1)∵与点A关于点中心对称点的特征是横纵坐标符号改变,
∵点,
∴点A关于点中心对称点的坐标为(-3,-2),
故答案为∶-3,-2;
(2)把点A、B顺时针旋转90°对应点分别为A1、B1,连结OA1、OB1、A1B1,则为所求如图,
点B1到y轴距离=点B到x轴的距离,点B1到x轴距离=点B到y轴的距离,
∵,点B1在第四象限,
∴点B1坐标为(3,-1);
(3)作点关于轴的对称点,连接交轴于点,
∵的坐标是.则,
PB=PB′,=PA+PB′≤AB′,
此时最短,
∵,,
∴.
【点睛】
本题考查中心对称,三角形旋转,轴对称以及两点之间线段最短,关键是利用轴对称作点B关于y轴对称点B′,点P、A、B′三点共线时距离最短.
23.如图所示,、点在轴上,将三角形沿轴负方向平移,平移后的图形为三角形,且点的坐标为,且.
(1)直接写出点的坐标 ;
(2)直接写出点的坐标 ;
【答案】(1);(2)
【解析】
【分析】
(1)根据二次根式的被开方数是非负数求出a、b值,即可得出答案;
(2)根据平移的性质即可得出点E坐标;
【详解】
解:(1),
,,
点的坐标为,
点的坐标为:;
故答案为:;
(2)点在轴上,点的坐标为:,
点向左平移了3个单位长度,
向左平移3个单位得到:
点的坐标为:,
故答案为:.
【点睛】
本题考查坐标与图形变换-平移、二次根式的性质,熟练掌握图形变换过程中点的坐标特征是解答的关键.
五、解答题(三)(本大题共2小题,每小题10分,共20分)
24.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;并写出点A2、B2、C2坐标;
(3)请画出△ABC绕O逆时针旋转90°后的△A3B3C3;并写出点A3、B3、C3坐标.
【答案】(1)见解析;(2)见解析,A2(﹣1,﹣1)、B2(﹣4,﹣2)、C2(﹣3,﹣4);(3)见解析,A3(﹣1,1)、B3(﹣2,4)、C3(﹣4,3).
【解析】
【分析】
(1)利用平移的性质得出对应点的位置进而得出答案
(2)利用关于原点对称点的性质得出对应点的位置进而得出答案
(3)利用旋转的性质得出旋转后的点的坐标进而得出答案
【详解】
解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求,A2(﹣1,﹣1)、B2(﹣4,﹣2)、C2(﹣3,﹣4);
(3)如图,△A3B3C3即为所求,A3(﹣1,1)、B3(﹣2,4)、C3(﹣4,3).
【点睛】
本题主要考查了二次函数平移旋转等图形变换的基本性质,掌握前后变换规律是解题关键
25.如图所示,每个小正方形的边长为1个单位长度,的顶点均在格点上,点、的坐标分别是、.
(1)点关于点中心对称的点的坐标为 ;
(2)绕点顺时针旋转后得到△,在图中画出△,并写出点的坐标: .
【答案】(1)
(2)图见解析,
【解析】
(1)
解:(1)如图,点即为所求作..
故答案为:.
(2)
(2)如图,△即为所求作,点的坐标.
故答案为:.
【点睛】
本题考查作图旋转变换,中心对称等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
_21?????????è?????(www.21cnjy.com)_
第三章《图形的平移与旋转》检测卷02
第I卷(选择题)
选择题(本大题共10小题,每小题3分,共30分)
1.在平面直角坐标系中,点关于原点对称点在()
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.下列各徽标中,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
3.已知点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,则( )
A.x=﹣1,y=2 B.x=﹣1,y=8 C.x=﹣1,y=﹣2 D.x=1,y=8
4.如图,沿射线方向平移到(点E在线段上),如果,,那么平移距离为(???????)
A.3cm B.5cm C.8cm D.13cm
5.如图,在中,,将绕点逆时针旋转到的位置,使得,则的度数是(???????)
A. B. C. D.
6.下列四个图形中,中心对称图形是(???????)
A. B. C. D.
7.如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一直线上,则三角板ABC旋转的度数是(??????? ).
A.60° B.90° C.120° D.150°
8.京剧脸谱、剪纸等图案一般蕴含着对称美,下列选取的图片中既是轴对称图形,又是中心对称图形的是(???????)
A. B. C. D.
9.下列图形中既是轴对称图形,也是中心对称图形的是(?????)
A. B. C. D.
10.如图,在平面直角坐标系中,线段的两个端点是,.将线段沿某一方向平移后,若点的对应点的坐标为,则点的对应点的坐标为(???????)
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共7小题,每小题4分,共28分)
11.如图,将正方形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点A,B,C的坐标分别为,,.是关于轴的对称图形,将绕点逆时针旋转180°,点的对应点为M,则点M的坐标为________.
12.如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE=_______.
13.如图,三角形中,,D是BC上一点,三角形逆时针旋转后到达三角形的位置.
(1)旋转中心是_________;
(2)旋转了_________度.
14.如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为_____.
15.如图,已知∠1=75°,将直线m平行移动到直线n的位置,则∠2﹣∠3=_____°.
16.如图,某住宅小区内有一长方形地,若在长方形地内修筑同样宽的小路(图中阴影都分),余下部分绿化,小路的宽均为2m,则绿化的面积为____.
17.若点和关于原点对称,则的值是___________.
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.画图并填空:
如图,在128 的方格纸中,每个小正方形的边长都为1 ,△ABC 的顶点都在方格纸的格点上,将△ABC 按照某方向经过一次平移后得到△A' B'C ' ,图中标出了点C 的对应点C ' .
(1)请画出△A' B'C ' ;
(2)利用方格纸,在△ABC 中画出AC 边上的中线BD 和BC 边上的高AE ;
(3)点F 为方格纸上的格点(异于点B ),若S ACB S ACF ,则图中格点F 共有 个.(请在方格纸中标出点F )
19.如图,在平面直角坐标系中,的三个顶点坐标分别为、、.
(1)点B关于坐标原点O对称的点的坐标为____________________;
(2)将绕点C顺时针旋转,画出旋转后得到的.
20.已知△是由经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△
(1)观察表中各对应点坐标的变化,并填空:
, , ;
(2)在平面直角坐标系中画出及平移后的△;
(3)直接写出△的面积是 .
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.如图,在等边中,D为BC边上一点,连接AD,将沿AD翻折得到,连接BE并延长交AD的延长线于点F,连接CF.
(1)若,求的度数;
(2)若,求的大小;
(3)猜想CF,BF,AF之间的数量关系,并证明.
22.如图网格中,的顶点均在格点上,点、的坐标分别是、.
(1)点A关于点中心对称点的坐标为(_______,_______);
(2)绕点顺时针旋转后得到,在方格纸中画出,并写出点的坐标(______,_______);
(3)在轴上找一点,使得最小,请在图中标出点的位置,并求出这个最小值.
23.如图所示,、点在轴上,将三角形沿轴负方向平移,平移后的图形为三角形,且点的坐标为,且.
(1)直接写出点的坐标 ;
(2)直接写出点的坐标 ;
五、解答题(三)(本大题共2小题,每小题10分,共20分)
24.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;并写出点A2、B2、C2坐标;
(3)请画出△ABC绕O逆时针旋转90°后的△A3B3C3;并写出点A3、B3、C3坐标.
25.如图所示,每个小正方形的边长为1个单位长度,的顶点均在格点上,点、的坐标分别是、.
(1)点关于点中心对称的点的坐标为 ;
(2)绕点顺时针旋转后得到△,在图中画出△,并写出点的坐标: .
第三章《图形的平移与旋转》检测卷02
第I卷(选择题)
选择题(本大题共10小题,每小题3分,共30分)
1.在平面直角坐标系中,点关于原点对称点在()
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D
【解析】
【分析】
先依据,即可得出点P所在的象限,再根据两个点关于原点对称时,它们的坐标符号相反,即可得出结论.
【详解】
解:∵,∴点在第二象限,
∴点关于原点对称点在第四象限.
故选D.
【点睛】
本题主要考查了关于原点对称的两个点的坐标特征,明确关于原点对称的两个点的横、纵坐标均互为相反数是解答的关键.
2.下列各徽标中,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
【答案】C
【解析】
【分析】
根据轴对称图形的定义和中心对称图形的定义,分别进行判断,即可得到答案.
【详解】
解:A、不是轴对称图形,也不是中心对称图形,故A错误;
B、是轴对称图形,也是中心对称图形,故B错误;
C、是轴对称图形,但不是中心对称图形,故C正确;
D、不是轴对称图形,也不是中心对称图形,故D错误;
故选:C.
【点睛】
本题考查了轴对称图形和中心对称图形的识别,解题的关键是熟记定义.
3.已知点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,则( )
A.x=﹣1,y=2 B.x=﹣1,y=8 C.x=﹣1,y=﹣2 D.x=1,y=8
【答案】A
【解析】
【分析】
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点是P′(﹣x,﹣y).直接利用关于原点对称点的性质得出x,y的值进而得出答案.
【详解】
解:∵点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,
∴x﹣2+x+4=0,y﹣5=﹣3,
解得:x=﹣1,y=2,
故选:A.
【点睛】
此题主要考查了关于原点对称点的性质,正确把握横纵坐标的关系是解题关键.
4.如图,沿射线方向平移到(点E在线段上),如果,,那么平移距离为(???????)
A.3cm B.5cm C.8cm D.13cm
【答案】A
【解析】
【分析】
观察图象,发现平移前后,B、E对应,C、F对应,根据平移的性质,易得平移的距离=BE,进而可得答案.
【详解】
解:根据平移的性质,
易得平移的距离=BE=8-5=3cm,
故选:A.
【点睛】
本题考查平移的性质,经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等,本题关键要找到平移的对应点.
5.如图,在中,,将绕点逆时针旋转到的位置,使得,则的度数是(???????)
A. B. C. D.
【答案】C
【解析】
【分析】
根据旋转的性质得AC′=AC,∠B′AB=∠C′AC,再根据等腰三角形的性质得∠AC′C=∠ACC′,然后根据平行线的性质由CC′∥AB得∠ACC′=∠CAB=70°,则∠AC′C=∠ACC′=70°,再根据三角形内角和计算出∠CAC′=40°,所以∠B′AB=40°.
【详解】
∵绕点逆时针旋转到的位置,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,
故选C.
【点睛】
本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了平行线的性质.
6.下列四个图形中,中心对称图形是(???????)
A. B. C. D.
【答案】D
【解析】
【分析】
根据中心对称图形的概念结合各图形的特点求解.
【详解】
解:A、不是中心对称图形,不符合题意;
B、不是中心对称图形,不符合题意;
C、不是中心对称图形,不符合题意;
D、是中心对称图形,符合题意.
故选:D.
【点睛】
本题考查了中心对称图形与轴对称图形的概念.判断中心对称图形是要寻找对称中心,图形旋转180度后与原图形重合.
7.如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一直线上,则三角板ABC旋转的度数是(??????? ).
A.60° B.90° C.120° D.150°
【答案】D
【解析】
【分析】
根据旋转角的定义,两对应边的夹角就是旋转角,即可求解.
【详解】
解: 旋转角是∠CAC′=180°﹣30°=150°.
故选D.
【点睛】
考点:旋转的性质.
8.京剧脸谱、剪纸等图案一般蕴含着对称美,下列选取的图片中既是轴对称图形,又是中心对称图形的是(???????)
A. B. C. D.
【答案】D
【解析】
【分析】
根据轴对称图形与中心对称图形的概念进行判断.
【详解】
解:A、是轴对称图形,不是中心对称图形,故本选项不合题意;
B、不是轴对称图形,也不是中心对称图形,故本选项不合题意;
C、不是轴对称图形,是中心对称图形,故本选项不合题意;
D、既是轴对称图形,又是中心对称图形,故本选项符合题意.
故选:D.
【点睛】
本题考查了中心对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
9.下列图形中既是轴对称图形,也是中心对称图形的是(?????)
A. B. C. D.
【答案】B
【解析】
【分析】
根据轴对称图形与中心对称图形的概念求解.
【详解】
解:A、既不是轴对称图形,也不是中心对称图形,故此选项不符合题意;
B、既是轴对称图形,也是中心对称图形,故此选项符合题意;
C、是轴对称图形,不是中心对称图形,故此选项不符合题意;
D、不是轴对称图形,是中心对称图形,故此选项不符合题意.
故选:B.
【点睛】
此题主要考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
10.如图,在平面直角坐标系中,线段的两个端点是,.将线段沿某一方向平移后,若点的对应点的坐标为,则点的对应点的坐标为(???????)
A. B. C. D.
【答案】C
【解析】
【分析】
观察点到的变化特征:横坐标减小3,纵坐标减小3,根据图形平移的性质解题即可.
【详解】
平移后得到
横坐标减小3,纵坐标减小3,
即
故选:C.
【点睛】
本题考查坐标与图形、平移等知识,是重要考点,难度较易,掌握相关知识是解题关键.
第II卷(非选择题)
二、填空题(本大题共7小题,每小题4分,共28分)
11.如图,将正方形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点A,B,C的坐标分别为,,.是关于轴的对称图形,将绕点逆时针旋转180°,点的对应点为M,则点M的坐标为________.
【答案】
【解析】
【分析】
根据题意,画出旋转后图形,即可求解
【详解】
解:如图,将绕点逆时针旋转180°,所以点的对应点为M的坐标为.
故答案为:
【点睛】
本题考查平面直角坐标系内图形的对称,旋转,解题关键是理解对称旋转的含义,并结合网格解题.
12.如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE=_______.
【答案】3.
【解析】
【详解】
试题分析:∵将△ABC绕点A顺时针旋转60°得到△AED,∴∠BAE=60°,AB=AE,∴△BAE是等边三角形,∴BE=3.故答案为3.
考点:旋转的性质.
13.如图,三角形中,,D是BC上一点,三角形逆时针旋转后到达三角形的位置.
(1)旋转中心是_________;
(2)旋转了_________度.
【答案】???? 点A???? 60
【解析】
【分析】
根据等边三角形的性质得AB=AC,∠BAC=60°,然后根据旋转的求解.
【详解】
解:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵点△ABD经过旋转后到达△ACE的位置,
∴旋转中心是点A,∠BAC等于旋转角,即逆时针旋转了60度.
故答案为:点A、60.
【点睛】
本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
14.如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为_____.
【答案】
【解析】
【详解】
试题分析:∵在等边△ABC中,∠B=60°,AB=6,D是BC的中点,∴AD⊥BD,∠BAD=∠CAD=30°.
∴AD=ABcos30°=6×.
根据旋转的性质知,∠EAC=∠DAB=30°,AD=AE,
∴∠DAE=∠EAC+∠BAD=60°.∴△ADE的等边三角形.
∴DE=AD=,即线段DE的长度为.
15.如图,已知∠1=75°,将直线m平行移动到直线n的位置,则∠2﹣∠3=_____°.
【答案】105
【解析】
【分析】
直接利用平移的性质结合三角形外角的性质得出答案.
【详解】
解:如图,由题意可得:mn,
∴∠CAD+∠1=180°.
∵∠3=∠4,
∴∠4+∠CAD=∠2,
∴∠2﹣∠3=∠CAD+∠3﹣∠3=∠CAD=180°﹣∠1=180°﹣75°=105°.
故答案为:105.
【点睛】
本题考查了平移的性质、三角形外角的性质以及平行线的性质,正确转化角的关系是解题的关键.
16.如图,某住宅小区内有一长方形地,若在长方形地内修筑同样宽的小路(图中阴影都分),余下部分绿化,小路的宽均为2m,则绿化的面积为____.
【答案】540
【解析】
【分析】
利用平移把不规则的图形变为规则图形,如此一来,所有绿化面积之和就变为了(32-2)(20-2)m2,进而即可求出答案.
【详解】
利用平移可得,两条小路的总面积是:(32-2)(20-2)=540(m2).
故答案为540.
【点睛】
此题主要考查了生活中的平移现象,这类题目体现了数形结合的思想,需利用平移把不规则的图形变为规则图形,进而即可列出方程,求出答案.
17.若点和关于原点对称,则的值是___________.
【答案】-3.
【解析】
【分析】
先求出的值,然后相加即可.
【详解】
解:点和关于原点对称,
则a=-1,b=-2,
,
故答案为:-3.
【点睛】
本题考查了关于原点对称点的坐标变化规律,解题关键是熟知变化规律,准确进行计算.
三、解答题(一)(本大题共3小题,每小题6分,共18分)
18.画图并填空:
如图,在128 的方格纸中,每个小正方形的边长都为1 ,△ABC 的顶点都在方格纸的格点上,将△ABC 按照某方向经过一次平移后得到△A' B'C ' ,图中标出了点C 的对应点C ' .
(1)请画出△A' B'C ' ;
(2)利用方格纸,在△ABC 中画出AC 边上的中线BD 和BC 边上的高AE ;
(3)点F 为方格纸上的格点(异于点B ),若S ACB S ACF ,则图中格点F 共有 个.(请在方格纸中标出点F )
【答案】(1)见解析;(2)见解析;(3)5
【解析】
【分析】
(1)利用点C和C′的位置确定平移的方向与距离,然后利用此平移规律画出A、B的对应点即可;
(2)利用网格特点确定AC的中点D,从而得到中线BD;再利用网格特点过A点作BC的垂线,确定垂足E点;
(3)过B点作AC的平行线可确定2个格点F,把直线AC向右平移个单位,再向上平移1个单位得到3个格点F.
【详解】
解:(1)如图,△A'B'C'为所作;
(2)如图,BD、AE为所作;
(3)若S△ACB=S△ACF,则图中格点F共有5个,如图.
故答案为5.
【点睛】
本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
19.如图,在平面直角坐标系中,的三个顶点坐标分别为、、.
(1)点B关于坐标原点O对称的点的坐标为____________________;
(2)将绕点C顺时针旋转,画出旋转后得到的.
【答案】(1);(2)见解析
【解析】
【分析】
(1)根据关于原点对称的点的坐标特征写出B关于原点的对称点的坐标即可;
(2)利用网格特点和旋转的性质画出点A、B的对应点A1、B1,从而得到△A1B1C.
【详解】
解:(1)∵B(?1,1),
∴点B关于原点的对称点的坐标为(1,-1),
故答案为:(1,-1);
(2)如图,△A1B1C为所作;
【点睛】
本题考查了作图-旋转变换,关于原点对称的两个点的坐标特点,解决本题的关键是掌握旋转的性质.
20.已知△是由经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△
(1)观察表中各对应点坐标的变化,并填空:
, , ;
(2)在平面直角坐标系中画出及平移后的△;
(3)直接写出△的面积是 .
【答案】(1)-2,6,8;(2)见解析;(3)9
【解析】
【分析】
(1)观察表中各对应点坐标的变化,△是由△ABC经过向上平移3个单位,向右平移6个单位得到的,进而可填空;
(2)根据(1)即可在平面直角坐标系中画出△ABC及平移后的△;
(3)根据割补法即可求出△的面积.
【详解】
(1)观察表中点和点坐标的变化,点和点坐标的变化可知:
△是由经过向上平移3个单位,向右平移6个单位得到的,
,,;
故答案为:,6,8;
(2)如图,及△即为所求;
(3)△的面积为:.
故答案为:9.
【点睛】
本题考查了作图-平移变换,解决本题的关键是掌握平移的性质.
四、解答题(二)(本大题共3小题,每小题8分,共24分)
21.如图,在等边中,D为BC边上一点,连接AD,将沿AD翻折得到,连接BE并延长交AD的延长线于点F,连接CF.
(1)若,求的度数;
(2)若,求的大小;
(3)猜想CF,BF,AF之间的数量关系,并证明.
【答案】(1)20°;(2);(3)AF= CF+BF,理由见解析
【解析】
【分析】
(1)由△ABC是等边三角形,得到AB=AC,∠BAC=∠ABC=60°,由折叠的性质可知,∠EAD=∠CAD=20°,AC=AE,则∠BAE=∠BAC-∠EAD-∠CAD=20°,AB=AE,,∠CBF=∠ABE-∠ABC=20°;
(2)同(1)求解即可;
(3)如图所示,将△ABF绕点A逆时针旋转60°得到△ACG,先证明△AEF≌△ACF得到∠AFE=∠AFC,然后证明∠AFE=∠AFC=60°,得到∠BFC=120°,即可证明F、C、G三点共线,得到△AFG是等边三角形,则AF=GF=CF+CG=CF+BF.
【详解】
解:(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ABC=60°,
由折叠的性质可知,∠EAD=∠CAD=20°,AC=AE,
∴∠BAE=∠BAC-∠EAD-∠CAD=20°,AB=AE,
∴,
∴∠CBF=∠ABE-∠ABC=20°;
(2)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ABC=60°,
由折叠的性质可知,,AC=AE,
∴ ,AB=AE,
∴,
∴;
(3)AF= CF+BF,理由如下:
如图所示,将△ABF绕点A逆时针旋转60°得到△ACG,
∴AF=AG,∠FAG=60°,∠ACG=∠ABF,BF=CG
在△AEF和△ACF中,
,
∴△AEF≌△ACF(SAS),
∴∠AFE=∠AFC,
∵∠CBF+∠BCF+∠BFD+∠CFD=180°,∠CAF+∠CFA+∠ACD+∠CFD=180°,
∴∠BFD=∠ACD=60°,
∴∠AFE=∠AFC=60°,
∴∠BFC=120°,
∴∠BAC+∠BFC=180°,
∴∠ABF+∠ACF=180°,
∴∠ACG+∠ACF=180°,
∴F、C、G三点共线,
∴△AFG是等边三角形,
∴AF=GF=CF+CG=CF+BF.
【点睛】
本题主要考查了等边三角形的性质与判定,旋转的性质,折叠的性质,全等三角形的性质与判定,三角形内角和定理,熟知相关知识是解题的关键.
22.如图网格中,的顶点均在格点上,点、的坐标分别是、.
(1)点A关于点中心对称点的坐标为(_______,_______);
(2)绕点顺时针旋转后得到,在方格纸中画出,并写出点的坐标(______,_______);
(3)在轴上找一点,使得最小,请在图中标出点的位置,并求出这个最小值.
【答案】(1)-3,-2;(2)作图见解析;3,-1;(3)点P的位置见解析;.
【解析】
【分析】
(1)关于点中心对称点的特征是横纵坐标符号相反,可得点A关于点中心对称点的坐标;
(2)把点A、B顺时针旋转90°对应点分别为A1、B1,连结OA1、OB1、A1B1,可得,进而可得各点坐标;
(3)作点关于轴的对称点,连接交轴于点,由勾股定理可得.
【详解】
解:(1)∵与点A关于点中心对称点的特征是横纵坐标符号改变,
∵点,
∴点A关于点中心对称点的坐标为(-3,-2),
故答案为∶-3,-2;
(2)把点A、B顺时针旋转90°对应点分别为A1、B1,连结OA1、OB1、A1B1,则为所求如图,
点B1到y轴距离=点B到x轴的距离,点B1到x轴距离=点B到y轴的距离,
∵,点B1在第四象限,
∴点B1坐标为(3,-1);
(3)作点关于轴的对称点,连接交轴于点,
∵的坐标是.则,
PB=PB′,=PA+PB′≤AB′,
此时最短,
∵,,
∴.
【点睛】
本题考查中心对称,三角形旋转,轴对称以及两点之间线段最短,关键是利用轴对称作点B关于y轴对称点B′,点P、A、B′三点共线时距离最短.
23.如图所示,、点在轴上,将三角形沿轴负方向平移,平移后的图形为三角形,且点的坐标为,且.
(1)直接写出点的坐标 ;
(2)直接写出点的坐标 ;
【答案】(1);(2)
【解析】
【分析】
(1)根据二次根式的被开方数是非负数求出a、b值,即可得出答案;
(2)根据平移的性质即可得出点E坐标;
【详解】
解:(1),
,,
点的坐标为,
点的坐标为:;
故答案为:;
(2)点在轴上,点的坐标为:,
点向左平移了3个单位长度,
向左平移3个单位得到:
点的坐标为:,
故答案为:.
【点睛】
本题考查坐标与图形变换-平移、二次根式的性质,熟练掌握图形变换过程中点的坐标特征是解答的关键.
五、解答题(三)(本大题共2小题,每小题10分,共20分)
24.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;并写出点A2、B2、C2坐标;
(3)请画出△ABC绕O逆时针旋转90°后的△A3B3C3;并写出点A3、B3、C3坐标.
【答案】(1)见解析;(2)见解析,A2(﹣1,﹣1)、B2(﹣4,﹣2)、C2(﹣3,﹣4);(3)见解析,A3(﹣1,1)、B3(﹣2,4)、C3(﹣4,3).
【解析】
【分析】
(1)利用平移的性质得出对应点的位置进而得出答案
(2)利用关于原点对称点的性质得出对应点的位置进而得出答案
(3)利用旋转的性质得出旋转后的点的坐标进而得出答案
【详解】
解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求,A2(﹣1,﹣1)、B2(﹣4,﹣2)、C2(﹣3,﹣4);
(3)如图,△A3B3C3即为所求,A3(﹣1,1)、B3(﹣2,4)、C3(﹣4,3).
【点睛】
本题主要考查了二次函数平移旋转等图形变换的基本性质,掌握前后变换规律是解题关键
25.如图所示,每个小正方形的边长为1个单位长度,的顶点均在格点上,点、的坐标分别是、.
(1)点关于点中心对称的点的坐标为 ;
(2)绕点顺时针旋转后得到△,在图中画出△,并写出点的坐标: .
【答案】(1)
(2)图见解析,
【解析】
(1)
解:(1)如图,点即为所求作..
故答案为:.
(2)
(2)如图,△即为所求作,点的坐标.
故答案为:.
【点睛】
本题考查作图旋转变换,中心对称等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
