【课件】第二章-§2函数 2.2函数的表示法 高中数学-北师大版-必修第一册(共48张PPT)
文档属性
| 名称 | 【课件】第二章-§2函数 2.2函数的表示法 高中数学-北师大版-必修第一册(共48张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 07:57:42 | ||
图片预览









文档简介
(共48张PPT)
高中数学-北师大版-必修第一册
§2 函 数
2.2 函数的表示法
第二章 函 数
学习目标
1.在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列举法、解析法)表示函数.
2.理解函数图象的作用.
3.通过具体实例,了解简单的分段函数,并能简单应用.
重点:函数的表示法.
难点:分段函数的表示及图象.
知识梳理
函数的表示方法
函数的表示方法通常有解析法、列表法和图象法.
取整函数
设x为任一实数,不超过x的最大整数称为x的整数部分,记作[x],如当x=3.14时,[x]=[3.14]=3;当x=-3.14时,[x]=[-3.14]=-4.
于是,我们把y=[x]叫作取整函数.
例1
一 函数的列表法与图象法表示
常考题型
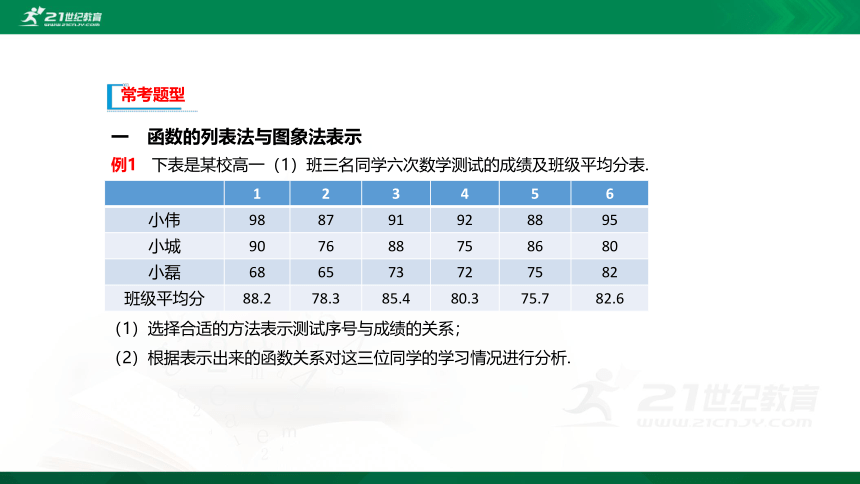
下表是某校高一(1)班三名同学六次数学测试的成绩及班级平均分表.
(1)选择合适的方法表示测试序号与成绩的关系;
(2)根据表示出来的函数关系对这三位同学的学习情况进行分析.
1 2 3 4 5 6
小伟 98 87 91 92 88 95
小城 90 76 88 75 86 80
小磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
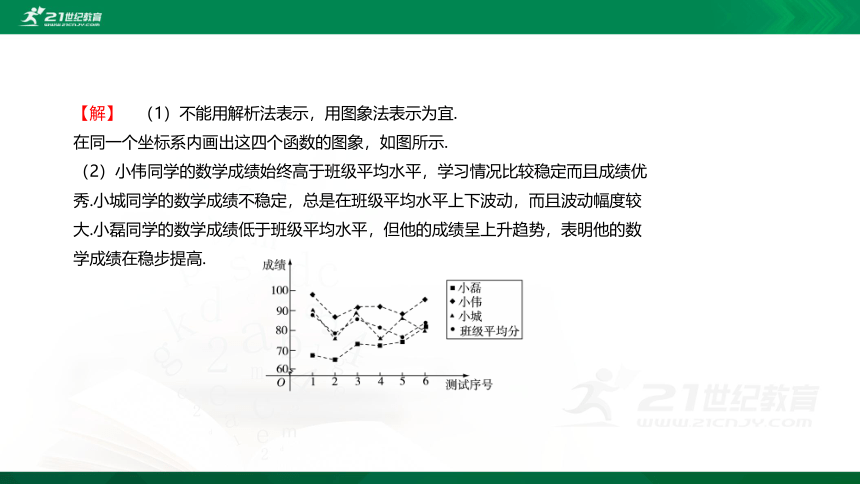
【解】 (1)不能用解析法表示,用图象法表示为宜.
在同一个坐标系内画出这四个函数的图象,如图所示.
(2)小伟同学的数学成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀.小城同学的数学成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大.小磊同学的数学成绩低于班级平均水平,但他的成绩呈上升趋势,表明他的数学成绩在稳步提高.
函数的三种表示方法及其优缺点
(1)解析法、列表法、图象法均是函数的表示方法,解析法是从“数”的方面简明、全面地概括了变量之间的数量关系;图象法从“形”的方面刻画了变量之间的数量关系;列表法可根据表格,由自变量x的取值查到和它对应的唯一的函数值y.
(2)三种表示方法各有优缺点,并不是所有的函数都能用解析法表示,解题时要根据需要选择适当的表示方法,无论用哪种方法表示函数,都必须满足函数的概念.
(3)在用三种方法表示函数时要注意:
①解析法必须注明函数的定义域;②列表法必须罗列出所有的自变量与函数值的对应关系;③图象法必须清楚函数图象是“点”还是“线”.
解题归纳
已知两个函数f(x)和g(x)的定义域和值域都是集合{1,2,3},其定义如下表.
训练题
1.
x 1 2 3
f(x) 2 3 1
x 1 2 3
g(x) 1 3 2
填写下列表格,其中三个数由左到右依次为 ( )
x 1 2 3
f(g(x))
A.2,1,3 B.1,2,3 C.3,2,1 D.1,3,2
A
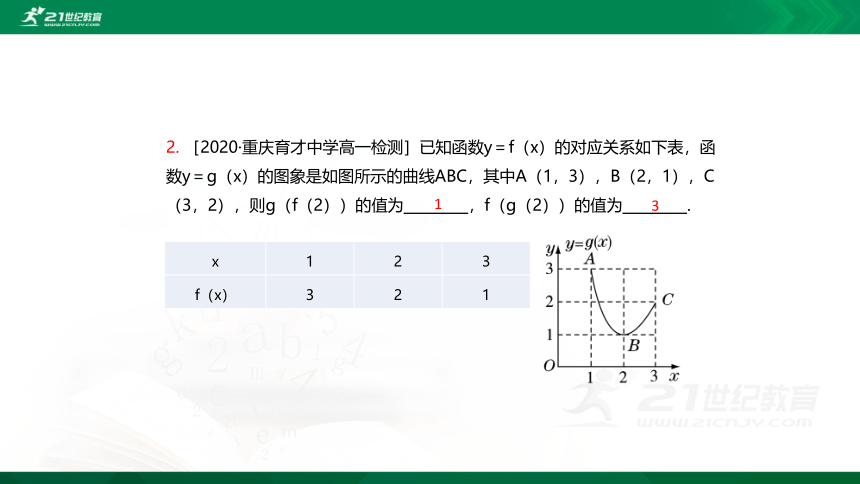
2. [2020·重庆育才中学高一检测]已知函数y=f(x)的对应关系如下表,函数y=g(x)的图象是如图所示的曲线ABC,其中A(1,3),B(2,1),C(3,2),则g(f(2))的值为 ,f(g(2))的值为 .
1
x 1 2 3
f(x) 3 2 1
3
例2
二 求函数的解析式
<1>已知函数类型求函数解析式
已知二次函数f(x)满足f(x+1)=f(x)+2x,且f(0)=1,求f(x)的解析式.
二次函数解析式的三种常见形式
(1)一般式:f(x)=ax2+bx+c(a≠0).
(2)顶点式:f(x)=a(x-m)2+n(a≠ 0,(m,n)为函数图象的顶点坐标).
(3)两根式:f(x)=a(x-x1)(x-x2)(a≠0,x1,x2为方程f(x)=0的两个实根).
解题时根据题设条件灵活选取即可.
解题归纳
训练题
训练题
例3
<2>用换元法、配凑法求函数解析式
用换元法(或配凑法)求函数解析式的思路
已知f(g(x))=h(x),求f(x),常用的两种方法:
①换元法,即令t=g(x),解出x,代入h(x),得到一个含t的解析式,然后把解析式中的t用x代替,注意换元后新元的范围.
②配凑法,即从f(g(x))的解析式中配凑出“g(x)”,用g(x)来表示h(x),然后将解析式中的g(x)用x代替即可.
解题归纳
训练题
1.
C
2.
<3>用消元法(或解方程组法)求函数解析式
例4
用消元法(或解方程组法)求函数解析式
在已知式子中,含有关于两个不同变量的函数,而这两个变量有着某种关系,这时就要根据两个变量的关系,建立一个新的关于这两个变量的式子,由这两个式子建立方程组,通过解方程组消去一个变量,得到目标变量的解析式,这种方法叫作消元法(或解方程组法),即已知f(x)与f(φ(x))满足的关系式,要求f(x)时,可用φ(x)代替两边所有的x,得到关于f(x)及f(φ(x))的方程组,解之即可求出f(x).
解题归纳
训练题
1.
2.
<4>求抽象函数的解析式
例5
若函数f(x)对一切实数x,y均有f(x+y)-f(y)=x(x+2y+1)成立,且f(1)=0,求f(x)的解析式.
【解】 ∵ f(x+y)-f(y)=x(x+2y+1)对任意实数x,y均成立,
∴ 可令x=1,y=0,得f(1)-f(0)=2.
∵ f(1)=0,∴ f(0)=-2.
令y=0得f(x)-f(0)=x(x+1),∴ f(x)+2=x2+x,
即f(x)=x2+x-2.
用赋值法求函数解析式
当所给的函数中含有两个变量时,可对这两个变量交替用特殊值代入,或使这两个变量相等代入,再根据已知条件求出函数解析式,具体取什么特殊值,要根据题目特征而定.需要说明的是,依据这样的关系式,不是都可以求出函数解析式的.
解题归纳
训练题
已知对任意实数x,y都有f(x+y)-2f(y)=x2+2xy-y2+3x-3y,求f(x).
解:(方法一)∵ f(x+y)- 2f(y)=x2+2xy-y2+3x-3y对任意实数x,y都成立,
∴ 可令x=y=0,得f(0)-2f(0)=0,即f(0)=0.
再令y=0,得f(x)-2f(0)=x2+3x,∴ f(x)=x2+3x.
(方法二)令x=0,得f(y)-2f(y)=-y2-3y,
即-f(y)=-y2-3y.因此f(y)=y2+3y.故f(x)=x2+3x.
三 函数图象问题
<1>函数图象的画法
例6
作出下列函数的图象并求出其值域.
x … 1 2 3 …
y … 4 2 1 2 3 …
(2)y=x2+2x=(x+1)2-1,x∈[-2,2].列表如下:
x -2 -1 0 1 2
y 0 -1 0 3 8
作出该函数的图象如图所示,图象是抛物线y=x2+2x在-2≤x≤2之间的部分,可得函数的值域是[-1,8].
归纳总结
(1)分段函数的图象应该分段画.
(2)在画图象的某一段时,可先画出该段解析式对应的整个图象,再在上面截取所要的图象.
(3)画出函数图象后,可直接得到函数的值域,故图象法是求函数值域的重要方法之一.
(4)一般地,函数y=|x-a|的图象关于直线x=a对称.
解题归纳
解题归纳
训练题
[2020·辽师附中高一检测]已知函数f(x)=x|x-2|.
(1)画出函数f(x)的大致图象;
(2)若方程f(x)=m有两个根,求实数m的取值集合;
(3)若方程f(x)=m有三个根,求实数m的取值集合.
(2)因为y=m与x无关,故其图象是平行于x轴的直线.f(x)=m有两个实根,
即曲线y=f(x)与直线y=m有两个交点,所以m=0或m=1,所以m∈{0,1}.
(3)观察图象,当0即f(x)=m有三个根,所以m∈(0,1).
<2>图象的识别
例8
[2020·山东师范大学附属中学高一检测]如图所示的4个图象中,与所给3件事吻合最好的顺序为( )
①小明离开学校不久,发现自己把作业本忘在教室,于是立刻返回教室取了作业本再回家;
②小明放学回家骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
③小明放学从学校出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
(1) (2) (3) (4)
A.(1)(2)(4) B.(4)(1)(2) C.(4)(1)(3) D.(4)(2)(3)
【解析】 ①根据回学校后,离开学校的距离又变为0,可判断①的图象开始后不久又回归为0,与(4)吻合;②由于途中遇到一次交通堵塞,可判断中间有一段函数值没有发生变化,与(1)吻合;③由于为了赶时间开始加速,可判断函数图象的上升速度越来越快,与(2)吻合.综上,所给4个图象中,与所给3件事吻合最好的顺序为(4)(1)(2).
【答案】 B
[2020·河南信阳高一检测]如图所示,平面图形中阴影部分的面积S是h(h∈[0,H])的函数,则该函数的图象大致是( )
训练题
D
A B C D
<3>图象的应用
例9
对于任意的实数x1,x2,min{x1,x2}表示x1,x2中较小的那个数.若f(x)=2-x2,g(x)=x,则min{f(x),g(x)}的最大值是 .
本题亦可直接在同一直角坐标系中,分别作出f(x)=2-x2,g(x)=x的图象,求出图象交点的横坐标x1,x2,则x1,x2将x轴分成三段,在每一段下方的图象便构成h(x)的图象,再从h(x)的图象上找出最高点的纵坐标,即为h(x)的最大值.
解题归纳
训练题
四 分段函数问题
<1>分段函数的求值问题
例10
解决分段函数求值问题的策略
(1)在求分段函数的值f(x0)时,首先判断x0属于定义域的哪个区间,然后把x0代入相应的关系式求解.
(2)分段函数是指自变量在不同的取值范围内,其对应法则也不同的函数,分段函数是一个函数,而不是多个函数.分段函数的定义域是各段定义域的并集,值域是各段值域的并集,故解分段函数时要分段求解.
(3)求f(f(f(a)))的值时,一般要遵循由里向外逐层计算的原则.
解题归纳
训练题
D
B
<2>不等式求参数问题
例11
【解题提示】 当a>0时,f(a)=-a2<0恒成立;
当a=0时,f(a)=-a2=0;
当a<0时,f(a)=a2+2a,此时,当a≤-2时,f(a)≥0,当-2故本题应当分四种情况讨论,分别求出f(a),从而求出f(f(a)),然后分别解不等式,综合可得结果.
解决分段函数求值问题的策略
(1)在求分段函数的值f(x0)时,首先判断x0属于定义域的哪个区间,然后把x0代入相应的关系式求解.
(2)分段函数是指自变量在不同的取值范围内,其对应法则也不同的函数,分段函数是一个函数,而不是多个函数.分段函数的定义域是各段定义域的并集,值域是各段值域的并集,故解分段函数时要分段求解.
(3)求f(f(f(a)))的值时,一般要遵循由里向外逐层计算的原则.
解题归纳
训练题
A
(-∞,-1)
小结
函数的表示方法
函数的表示方法通常有解析法、列表法和图象法.
取整函数
设x为任一实数,不超过x的最大整数称为x的整数部分,记作[x],如当x=3.14时,[x]=[3.14]=3;当x=-3.14时,[x]=[-3.14]=-4.
于是,我们把y=[x]叫作取整函数.
【戮力同心 共赴前程】
生如蝼蚁当立鸿鹄之志
命如纸薄应有不屈之心
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
高中数学-北师大版-必修第一册
§2 函 数
2.2 函数的表示法
第二章 函 数
学习目标
1.在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列举法、解析法)表示函数.
2.理解函数图象的作用.
3.通过具体实例,了解简单的分段函数,并能简单应用.
重点:函数的表示法.
难点:分段函数的表示及图象.
知识梳理
函数的表示方法
函数的表示方法通常有解析法、列表法和图象法.
取整函数
设x为任一实数,不超过x的最大整数称为x的整数部分,记作[x],如当x=3.14时,[x]=[3.14]=3;当x=-3.14时,[x]=[-3.14]=-4.
于是,我们把y=[x]叫作取整函数.
例1
一 函数的列表法与图象法表示
常考题型
下表是某校高一(1)班三名同学六次数学测试的成绩及班级平均分表.
(1)选择合适的方法表示测试序号与成绩的关系;
(2)根据表示出来的函数关系对这三位同学的学习情况进行分析.
1 2 3 4 5 6
小伟 98 87 91 92 88 95
小城 90 76 88 75 86 80
小磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
【解】 (1)不能用解析法表示,用图象法表示为宜.
在同一个坐标系内画出这四个函数的图象,如图所示.
(2)小伟同学的数学成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀.小城同学的数学成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大.小磊同学的数学成绩低于班级平均水平,但他的成绩呈上升趋势,表明他的数学成绩在稳步提高.
函数的三种表示方法及其优缺点
(1)解析法、列表法、图象法均是函数的表示方法,解析法是从“数”的方面简明、全面地概括了变量之间的数量关系;图象法从“形”的方面刻画了变量之间的数量关系;列表法可根据表格,由自变量x的取值查到和它对应的唯一的函数值y.
(2)三种表示方法各有优缺点,并不是所有的函数都能用解析法表示,解题时要根据需要选择适当的表示方法,无论用哪种方法表示函数,都必须满足函数的概念.
(3)在用三种方法表示函数时要注意:
①解析法必须注明函数的定义域;②列表法必须罗列出所有的自变量与函数值的对应关系;③图象法必须清楚函数图象是“点”还是“线”.
解题归纳
已知两个函数f(x)和g(x)的定义域和值域都是集合{1,2,3},其定义如下表.
训练题
1.
x 1 2 3
f(x) 2 3 1
x 1 2 3
g(x) 1 3 2
填写下列表格,其中三个数由左到右依次为 ( )
x 1 2 3
f(g(x))
A.2,1,3 B.1,2,3 C.3,2,1 D.1,3,2
A
2. [2020·重庆育才中学高一检测]已知函数y=f(x)的对应关系如下表,函数y=g(x)的图象是如图所示的曲线ABC,其中A(1,3),B(2,1),C(3,2),则g(f(2))的值为 ,f(g(2))的值为 .
1
x 1 2 3
f(x) 3 2 1
3
例2
二 求函数的解析式
<1>已知函数类型求函数解析式
已知二次函数f(x)满足f(x+1)=f(x)+2x,且f(0)=1,求f(x)的解析式.
二次函数解析式的三种常见形式
(1)一般式:f(x)=ax2+bx+c(a≠0).
(2)顶点式:f(x)=a(x-m)2+n(a≠ 0,(m,n)为函数图象的顶点坐标).
(3)两根式:f(x)=a(x-x1)(x-x2)(a≠0,x1,x2为方程f(x)=0的两个实根).
解题时根据题设条件灵活选取即可.
解题归纳
训练题
训练题
例3
<2>用换元法、配凑法求函数解析式
用换元法(或配凑法)求函数解析式的思路
已知f(g(x))=h(x),求f(x),常用的两种方法:
①换元法,即令t=g(x),解出x,代入h(x),得到一个含t的解析式,然后把解析式中的t用x代替,注意换元后新元的范围.
②配凑法,即从f(g(x))的解析式中配凑出“g(x)”,用g(x)来表示h(x),然后将解析式中的g(x)用x代替即可.
解题归纳
训练题
1.
C
2.
<3>用消元法(或解方程组法)求函数解析式
例4
用消元法(或解方程组法)求函数解析式
在已知式子中,含有关于两个不同变量的函数,而这两个变量有着某种关系,这时就要根据两个变量的关系,建立一个新的关于这两个变量的式子,由这两个式子建立方程组,通过解方程组消去一个变量,得到目标变量的解析式,这种方法叫作消元法(或解方程组法),即已知f(x)与f(φ(x))满足的关系式,要求f(x)时,可用φ(x)代替两边所有的x,得到关于f(x)及f(φ(x))的方程组,解之即可求出f(x).
解题归纳
训练题
1.
2.
<4>求抽象函数的解析式
例5
若函数f(x)对一切实数x,y均有f(x+y)-f(y)=x(x+2y+1)成立,且f(1)=0,求f(x)的解析式.
【解】 ∵ f(x+y)-f(y)=x(x+2y+1)对任意实数x,y均成立,
∴ 可令x=1,y=0,得f(1)-f(0)=2.
∵ f(1)=0,∴ f(0)=-2.
令y=0得f(x)-f(0)=x(x+1),∴ f(x)+2=x2+x,
即f(x)=x2+x-2.
用赋值法求函数解析式
当所给的函数中含有两个变量时,可对这两个变量交替用特殊值代入,或使这两个变量相等代入,再根据已知条件求出函数解析式,具体取什么特殊值,要根据题目特征而定.需要说明的是,依据这样的关系式,不是都可以求出函数解析式的.
解题归纳
训练题
已知对任意实数x,y都有f(x+y)-2f(y)=x2+2xy-y2+3x-3y,求f(x).
解:(方法一)∵ f(x+y)- 2f(y)=x2+2xy-y2+3x-3y对任意实数x,y都成立,
∴ 可令x=y=0,得f(0)-2f(0)=0,即f(0)=0.
再令y=0,得f(x)-2f(0)=x2+3x,∴ f(x)=x2+3x.
(方法二)令x=0,得f(y)-2f(y)=-y2-3y,
即-f(y)=-y2-3y.因此f(y)=y2+3y.故f(x)=x2+3x.
三 函数图象问题
<1>函数图象的画法
例6
作出下列函数的图象并求出其值域.
x … 1 2 3 …
y … 4 2 1 2 3 …
(2)y=x2+2x=(x+1)2-1,x∈[-2,2].列表如下:
x -2 -1 0 1 2
y 0 -1 0 3 8
作出该函数的图象如图所示,图象是抛物线y=x2+2x在-2≤x≤2之间的部分,可得函数的值域是[-1,8].
归纳总结
(1)分段函数的图象应该分段画.
(2)在画图象的某一段时,可先画出该段解析式对应的整个图象,再在上面截取所要的图象.
(3)画出函数图象后,可直接得到函数的值域,故图象法是求函数值域的重要方法之一.
(4)一般地,函数y=|x-a|的图象关于直线x=a对称.
解题归纳
解题归纳
训练题
[2020·辽师附中高一检测]已知函数f(x)=x|x-2|.
(1)画出函数f(x)的大致图象;
(2)若方程f(x)=m有两个根,求实数m的取值集合;
(3)若方程f(x)=m有三个根,求实数m的取值集合.
(2)因为y=m与x无关,故其图象是平行于x轴的直线.f(x)=m有两个实根,
即曲线y=f(x)与直线y=m有两个交点,所以m=0或m=1,所以m∈{0,1}.
(3)观察图象,当0
<2>图象的识别
例8
[2020·山东师范大学附属中学高一检测]如图所示的4个图象中,与所给3件事吻合最好的顺序为( )
①小明离开学校不久,发现自己把作业本忘在教室,于是立刻返回教室取了作业本再回家;
②小明放学回家骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
③小明放学从学校出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
(1) (2) (3) (4)
A.(1)(2)(4) B.(4)(1)(2) C.(4)(1)(3) D.(4)(2)(3)
【解析】 ①根据回学校后,离开学校的距离又变为0,可判断①的图象开始后不久又回归为0,与(4)吻合;②由于途中遇到一次交通堵塞,可判断中间有一段函数值没有发生变化,与(1)吻合;③由于为了赶时间开始加速,可判断函数图象的上升速度越来越快,与(2)吻合.综上,所给4个图象中,与所给3件事吻合最好的顺序为(4)(1)(2).
【答案】 B
[2020·河南信阳高一检测]如图所示,平面图形中阴影部分的面积S是h(h∈[0,H])的函数,则该函数的图象大致是( )
训练题
D
A B C D
<3>图象的应用
例9
对于任意的实数x1,x2,min{x1,x2}表示x1,x2中较小的那个数.若f(x)=2-x2,g(x)=x,则min{f(x),g(x)}的最大值是 .
本题亦可直接在同一直角坐标系中,分别作出f(x)=2-x2,g(x)=x的图象,求出图象交点的横坐标x1,x2,则x1,x2将x轴分成三段,在每一段下方的图象便构成h(x)的图象,再从h(x)的图象上找出最高点的纵坐标,即为h(x)的最大值.
解题归纳
训练题
四 分段函数问题
<1>分段函数的求值问题
例10
解决分段函数求值问题的策略
(1)在求分段函数的值f(x0)时,首先判断x0属于定义域的哪个区间,然后把x0代入相应的关系式求解.
(2)分段函数是指自变量在不同的取值范围内,其对应法则也不同的函数,分段函数是一个函数,而不是多个函数.分段函数的定义域是各段定义域的并集,值域是各段值域的并集,故解分段函数时要分段求解.
(3)求f(f(f(a)))的值时,一般要遵循由里向外逐层计算的原则.
解题归纳
训练题
D
B
<2>不等式求参数问题
例11
【解题提示】 当a>0时,f(a)=-a2<0恒成立;
当a=0时,f(a)=-a2=0;
当a<0时,f(a)=a2+2a,此时,当a≤-2时,f(a)≥0,当-2
解决分段函数求值问题的策略
(1)在求分段函数的值f(x0)时,首先判断x0属于定义域的哪个区间,然后把x0代入相应的关系式求解.
(2)分段函数是指自变量在不同的取值范围内,其对应法则也不同的函数,分段函数是一个函数,而不是多个函数.分段函数的定义域是各段定义域的并集,值域是各段值域的并集,故解分段函数时要分段求解.
(3)求f(f(f(a)))的值时,一般要遵循由里向外逐层计算的原则.
解题归纳
训练题
A
(-∞,-1)
小结
函数的表示方法
函数的表示方法通常有解析法、列表法和图象法.
取整函数
设x为任一实数,不超过x的最大整数称为x的整数部分,记作[x],如当x=3.14时,[x]=[3.14]=3;当x=-3.14时,[x]=[-3.14]=-4.
于是,我们把y=[x]叫作取整函数.
【戮力同心 共赴前程】
生如蝼蚁当立鸿鹄之志
命如纸薄应有不屈之心
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
