第九章 图形的相似单元测试题(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
《第九章 图形的相似》
单元测试题
(满分:100分 时间:60分钟)
一、选择题(每小题3分,共30分)
1.将两块长为a m、宽为b m的矩形红布加工成一块长为c m、宽为d m的矩形红布,有人就a,b,c,d的关系写出如下四个等式,不过他写错了一个,写错的那个是( )
2.如图,在△ABC中,点D在边BC上,连接AD,点E在边AC上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( )
第2题图 第3题图 第4题图
3.如图,△ABC经平移得到△DEF,AC,DE交于点G,则图中共有相似三角形( )
A.3对 B.4对 C.5对 D.6对
4.如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(2,4).点A在y轴的正半轴上,点C在x轴的正半轴上,P是BC的中点.以坐标原点O为位似中心,将矩形OABC放大为原图形的1.5倍,记点P的对应点为P1,则点P1的坐标为( )
A.(3,3) B.(3,2)或(-3,-2) C.(3,3)或(-3,-3) D.(2,3)或(-2,-3)
5.如果两个相似三角形的对应边上的高之比是3:5,周长之和是24,那么这两个三角形的周长分别为( )
A. 9和15 B. 10和14 C. 8和16 D. 11和13
6.如图,∠ACB=∠BDC=90°.要使△ABC∽△BCD,给出下列需要添加的条件:①AB∥CD;②BC =AC·CD;③ .其中,正确的是( )
A. ①② B. ①③ C. ②③ D. ①②③
第6题图 第7题图
7.如图,D,E分别是△ABC的边AB,BC上的点,且DE∥AC,AE,CD相交于点O,若25,则 与 的比是( )
A.1:25 B.1:5 C.1:4 D.1:3
8.如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G,若AF=2DF,则的值为( )
第8题图 第9题图 第10题图
9.如图,在矩形ABCD中,E是CD延长线上的一点,连接BE交AD于点F,连接CF,AB=1,BC=2.若△ABF与△CEF的面积相等,则DE的长为( )
A.1
10.如图,小明晚上由路灯A下的点B处走到点C处时,测得自己影子CD的长为1 m,他继续往前走3 m到达点E处(即CE=3 m),测得自己影子EF的长为2 m,若小明的身高是1.5 m,则路灯A的高度AB是( )
A.4.5 m B.6 m C.7.2 m D.8 m
二、填空题(每小题3分,共18分)
11.已知则,
12.如图,四边形ABCD与四边形A′B′C′D′位似,位似中心为点 则A′B′=_______.
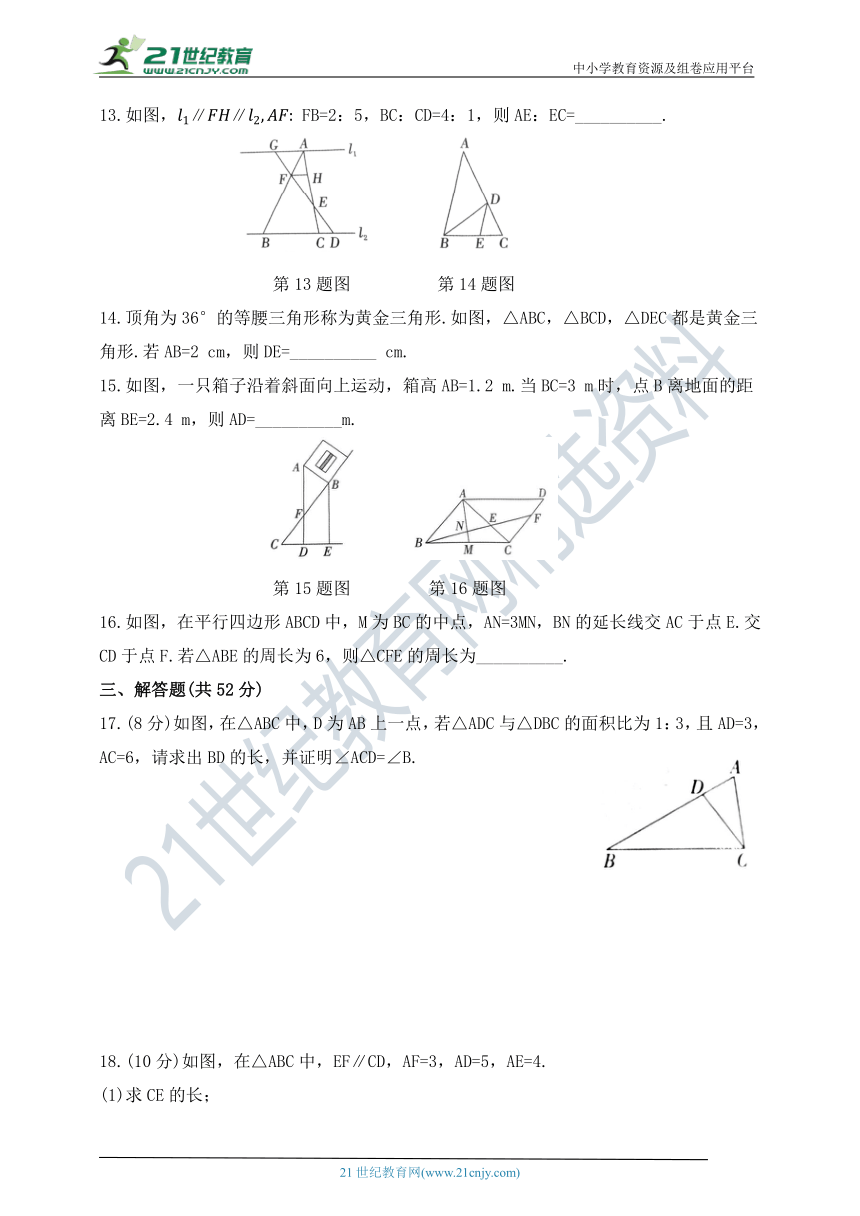
13.如图,∥∥ FB=2:5,BC:CD=4:1,则AE:EC=__________.
第13题图 第14题图
14.顶角为36°的等腰三角形称为黄金三角形.如图,△ABC,△BCD,△DEC都是黄金三角形.若AB=2 cm,则DE=__________ cm.
15.如图,一只箱子沿着斜面向上运动,箱高AB=1.2 m.当BC=3 m时,点B离地面的距离BE=2.4 m,则AD=__________m.
第15题图 第16题图
16.如图,在平行四边形ABCD中,M为BC的中点,AN=3MN,BN的延长线交AC于点E.交CD于点F.若△ABE的周长为6,则△CFE的周长为__________.
三、解答题(共52分)
17.(8分)如图,在△ABC中,D为AB上一点,若△ADC与△DBC的面积比为1:3,且AD=3,AC=6,请求出BD的长,并证明∠ACD=∠B.
18.(10分)如图,在△ABC中,EF∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)当 时,求证:DE∥BC .
19.(12分)如图①,△ABC三个顶点的坐标分别为A(2,7),B(6,8),C(8,2).
(1)以点O为位似中心,在第三象限内作出△A1B1C1,使△A1B1C1与△ABC的相似比为1:2,画出图形;
(2)分别写出点A1,B1,C1的坐标;
(3)如果△ABC内部一点M的坐标为(x,y),写出点M的对应点M1的坐标;
(4)在如图③所示的四个三角形中,与图②中的三角形相似的是__________,并说明理由.
20.(10分)大雁塔位于陕西省西安市城南大慈恩寺内,是全国著名的古代建筑,被视为古都西安的象征,小明和小华决定带着皮尺用自己学到的知识测量大雁塔的高度.恰逢雨后天晴,两人用如下方法测量:如图,小明半蹲在地上,小华站在小明和大雁塔之间,两人适当调整位置,当小明的眼睛A、小华的头顶C、塔顶E刚好在同一条直线上时,两人分别标注自己的位置B,D,用皮尺测出BD=1.2 m,且小华刚好在距离自己3.045 m的一小滩水(记为M)中看到了塔顶E(点B,D,M,F在同一条直线上).小华身高CD=1.6 m,小明蹲地观测时眼睛与地面之间的距离AB=1 m.请根据提供的相关信息,求大雁塔的高EF(结果精确到0.1 m).
21.(12分)如图,正方形PQMN在△ABC内,点P在AC上,点Q,M在AB上,点N在△ABC内,连接AN并延长交BC于点G,过点G作GD∥AB交AC于点D,过点D,G分别作DE⊥AB,GF⊥AB,垂足分别为E,F.
(1)求证:DG=GF;
(2)若AB=10,SABC=40,求四边形DEFG的面积.
参考答案
一、1.D 2.C 3.D 4.C 5.A 6.B 7.B 8.C 9.D 10.B
二、11. 12. 5 13. 2:1 14. 15. 3.12 16.4
三、17.∵△ADC的边AD上的高与△DBC的边BD上的高相同,且△ADC与△DBC的面积比为1:3,AD=3,∴BD=9. 即 又∵∠A=∠A,∴△∽△∴∠ACD=∠B .
18.(1)∵EF∥CD,△∵.解得
∽△
∴∠ADE=∠B.∴DE∥BC .
19.(1)△A1B1C1 如图所示
(2)点A1,B1,C1的坐标分别为
(3)点M 的坐标为(
(4)乙 理由:令题图②③中各小正方形的边长为1.根据勾股定理,题图②中的三角形的三边长分别为∴三边之比为 .甲中三角形三边之比为 乙中三角形三边之比为 丙中三角形三边之比为2:3:;丁中三角形三边之比为 ::4.根据三边对应成比例,两三角形相似,可得与题图②中的三角形相似的是乙.
过点A作AG⊥EF于点G,交CD于点H,则AG=BF,AH=BD=1.2 m,GF=AB=HD=1 m,CH=CD-HD=1.6-1=0.6(m).设EF=x m,则EG=(x-1) m.由题意,可得∠CMD=∠EMF,∠CDM=∠F=90°,∴△CDM∽△EFM.∴.∵CD=1.6 m,MD=3.045 m, m.由题意,得CH∥EG,∴∠ACH=∠AEG.又∵∠CAH=∠EAG,∴△∽△即解得x≈64.5.∴大雁塔的高EF约为64.5 m .
(1)∵四边形PQMN是正方形,∴MN⊥AB,MN=PN.∵GD∥AB,DE⊥AB,GF⊥AB,∴易得四边形DEFG是矩形,GF∥MN.∴∠AMN=∠AFG.又∵∠MAN=∠FAG,∴△∽△同理可得 ,∴DG=GF .
(2)如图,过点C作CH⊥AB于点H,交DG于点K.∵S△ABC=40, =8.∵GD∥AB,∴∠CDG=∠CAB.又∵∠DCG=∠ACB,∴△CDG∽△CAB.∴即 解得 四边形DEFG为正方形. ,即四边形DEFG的面积为 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
《第九章 图形的相似》
单元测试题
(满分:100分 时间:60分钟)
一、选择题(每小题3分,共30分)
1.将两块长为a m、宽为b m的矩形红布加工成一块长为c m、宽为d m的矩形红布,有人就a,b,c,d的关系写出如下四个等式,不过他写错了一个,写错的那个是( )
2.如图,在△ABC中,点D在边BC上,连接AD,点E在边AC上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( )
第2题图 第3题图 第4题图
3.如图,△ABC经平移得到△DEF,AC,DE交于点G,则图中共有相似三角形( )
A.3对 B.4对 C.5对 D.6对
4.如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(2,4).点A在y轴的正半轴上,点C在x轴的正半轴上,P是BC的中点.以坐标原点O为位似中心,将矩形OABC放大为原图形的1.5倍,记点P的对应点为P1,则点P1的坐标为( )
A.(3,3) B.(3,2)或(-3,-2) C.(3,3)或(-3,-3) D.(2,3)或(-2,-3)
5.如果两个相似三角形的对应边上的高之比是3:5,周长之和是24,那么这两个三角形的周长分别为( )
A. 9和15 B. 10和14 C. 8和16 D. 11和13
6.如图,∠ACB=∠BDC=90°.要使△ABC∽△BCD,给出下列需要添加的条件:①AB∥CD;②BC =AC·CD;③ .其中,正确的是( )
A. ①② B. ①③ C. ②③ D. ①②③
第6题图 第7题图
7.如图,D,E分别是△ABC的边AB,BC上的点,且DE∥AC,AE,CD相交于点O,若25,则 与 的比是( )
A.1:25 B.1:5 C.1:4 D.1:3
8.如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E,交AD于点F,交CD的延长线于点G,若AF=2DF,则的值为( )
第8题图 第9题图 第10题图
9.如图,在矩形ABCD中,E是CD延长线上的一点,连接BE交AD于点F,连接CF,AB=1,BC=2.若△ABF与△CEF的面积相等,则DE的长为( )
A.1
10.如图,小明晚上由路灯A下的点B处走到点C处时,测得自己影子CD的长为1 m,他继续往前走3 m到达点E处(即CE=3 m),测得自己影子EF的长为2 m,若小明的身高是1.5 m,则路灯A的高度AB是( )
A.4.5 m B.6 m C.7.2 m D.8 m
二、填空题(每小题3分,共18分)
11.已知则,
12.如图,四边形ABCD与四边形A′B′C′D′位似,位似中心为点 则A′B′=_______.
13.如图,∥∥ FB=2:5,BC:CD=4:1,则AE:EC=__________.
第13题图 第14题图
14.顶角为36°的等腰三角形称为黄金三角形.如图,△ABC,△BCD,△DEC都是黄金三角形.若AB=2 cm,则DE=__________ cm.
15.如图,一只箱子沿着斜面向上运动,箱高AB=1.2 m.当BC=3 m时,点B离地面的距离BE=2.4 m,则AD=__________m.
第15题图 第16题图
16.如图,在平行四边形ABCD中,M为BC的中点,AN=3MN,BN的延长线交AC于点E.交CD于点F.若△ABE的周长为6,则△CFE的周长为__________.
三、解答题(共52分)
17.(8分)如图,在△ABC中,D为AB上一点,若△ADC与△DBC的面积比为1:3,且AD=3,AC=6,请求出BD的长,并证明∠ACD=∠B.
18.(10分)如图,在△ABC中,EF∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)当 时,求证:DE∥BC .
19.(12分)如图①,△ABC三个顶点的坐标分别为A(2,7),B(6,8),C(8,2).
(1)以点O为位似中心,在第三象限内作出△A1B1C1,使△A1B1C1与△ABC的相似比为1:2,画出图形;
(2)分别写出点A1,B1,C1的坐标;
(3)如果△ABC内部一点M的坐标为(x,y),写出点M的对应点M1的坐标;
(4)在如图③所示的四个三角形中,与图②中的三角形相似的是__________,并说明理由.
20.(10分)大雁塔位于陕西省西安市城南大慈恩寺内,是全国著名的古代建筑,被视为古都西安的象征,小明和小华决定带着皮尺用自己学到的知识测量大雁塔的高度.恰逢雨后天晴,两人用如下方法测量:如图,小明半蹲在地上,小华站在小明和大雁塔之间,两人适当调整位置,当小明的眼睛A、小华的头顶C、塔顶E刚好在同一条直线上时,两人分别标注自己的位置B,D,用皮尺测出BD=1.2 m,且小华刚好在距离自己3.045 m的一小滩水(记为M)中看到了塔顶E(点B,D,M,F在同一条直线上).小华身高CD=1.6 m,小明蹲地观测时眼睛与地面之间的距离AB=1 m.请根据提供的相关信息,求大雁塔的高EF(结果精确到0.1 m).
21.(12分)如图,正方形PQMN在△ABC内,点P在AC上,点Q,M在AB上,点N在△ABC内,连接AN并延长交BC于点G,过点G作GD∥AB交AC于点D,过点D,G分别作DE⊥AB,GF⊥AB,垂足分别为E,F.
(1)求证:DG=GF;
(2)若AB=10,SABC=40,求四边形DEFG的面积.
参考答案
一、1.D 2.C 3.D 4.C 5.A 6.B 7.B 8.C 9.D 10.B
二、11. 12. 5 13. 2:1 14. 15. 3.12 16.4
三、17.∵△ADC的边AD上的高与△DBC的边BD上的高相同,且△ADC与△DBC的面积比为1:3,AD=3,∴BD=9. 即 又∵∠A=∠A,∴△∽△∴∠ACD=∠B .
18.(1)∵EF∥CD,△∵.解得
∽△
∴∠ADE=∠B.∴DE∥BC .
19.(1)△A1B1C1 如图所示
(2)点A1,B1,C1的坐标分别为
(3)点M 的坐标为(
(4)乙 理由:令题图②③中各小正方形的边长为1.根据勾股定理,题图②中的三角形的三边长分别为∴三边之比为 .甲中三角形三边之比为 乙中三角形三边之比为 丙中三角形三边之比为2:3:;丁中三角形三边之比为 ::4.根据三边对应成比例,两三角形相似,可得与题图②中的三角形相似的是乙.
过点A作AG⊥EF于点G,交CD于点H,则AG=BF,AH=BD=1.2 m,GF=AB=HD=1 m,CH=CD-HD=1.6-1=0.6(m).设EF=x m,则EG=(x-1) m.由题意,可得∠CMD=∠EMF,∠CDM=∠F=90°,∴△CDM∽△EFM.∴.∵CD=1.6 m,MD=3.045 m, m.由题意,得CH∥EG,∴∠ACH=∠AEG.又∵∠CAH=∠EAG,∴△∽△即解得x≈64.5.∴大雁塔的高EF约为64.5 m .
(1)∵四边形PQMN是正方形,∴MN⊥AB,MN=PN.∵GD∥AB,DE⊥AB,GF⊥AB,∴易得四边形DEFG是矩形,GF∥MN.∴∠AMN=∠AFG.又∵∠MAN=∠FAG,∴△∽△同理可得 ,∴DG=GF .
(2)如图,过点C作CH⊥AB于点H,交DG于点K.∵S△ABC=40, =8.∵GD∥AB,∴∠CDG=∠CAB.又∵∠DCG=∠ACB,∴△CDG∽△CAB.∴即 解得 四边形DEFG为正方形. ,即四边形DEFG的面积为 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
