人教版七年级数学下册5.3.1平行线的性质课件(共20张PPT)
文档属性
| 名称 | 人教版七年级数学下册5.3.1平行线的性质课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 12:54:03 | ||
图片预览





文档简介
(共20张PPT)
新人教版义务教育教科书
七年级数学
5.3.1 平行线的性质
判定方法1 同位角相等,两直线平行.
判定方法2 内错角相等,两直线平行.
判定方法3 同旁内角互补,两直线平行.
梳理旧知,引出新课
结论
平行线的判定
两
直
线
平
行
梳理旧知,引出新课
条件
结论
?
两条平行线
被第三条直
线所截
梳理旧知,引出新课
条件
结论
同位角?
内错角?
同旁内角?
a
b
c
探究:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图中的一组同位角. 它们有怎样的数量关系?你是怎样得到的?
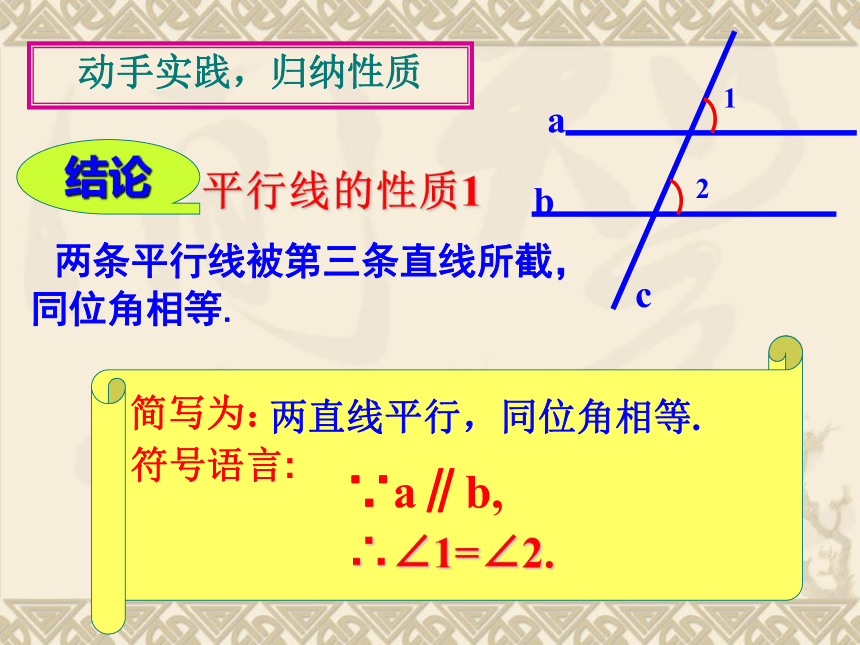
动手实践,归纳性质
两直线平行,同位角相等.
平行线的性质1
结论
两条平行线被第三条直线所截,
同位角相等.
∴∠1=∠2.
∵a∥b,
简写为:
符号语言:
b
1
2
a
c
动手实践,归纳性质
思考:
上一节,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”。类似地,你能出性质1,推出两条平行线被第三条直线截得的内错角之间的关系吗?
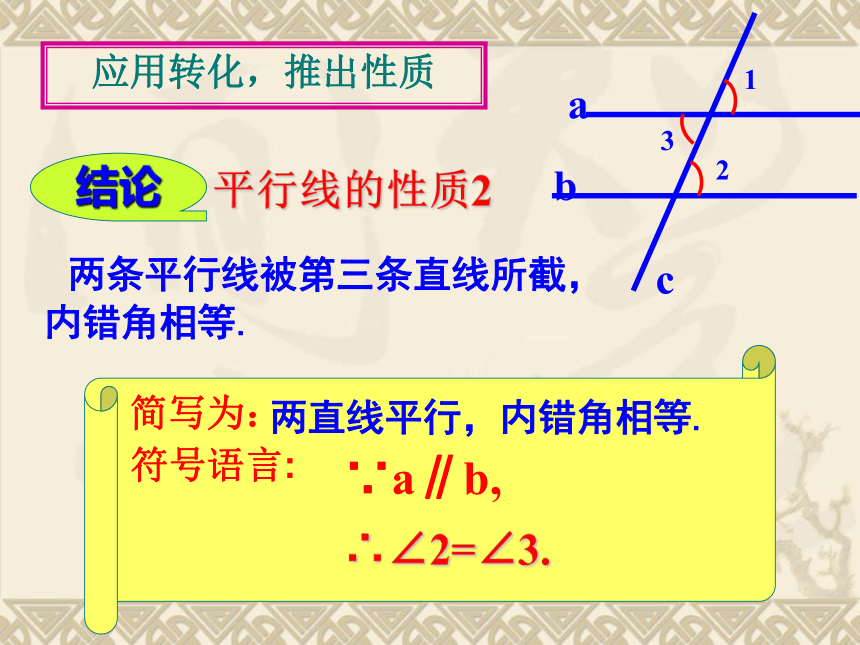
应用转化,推出性质
两直线平行,内错角相等.
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
∴∠2=∠3.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
3
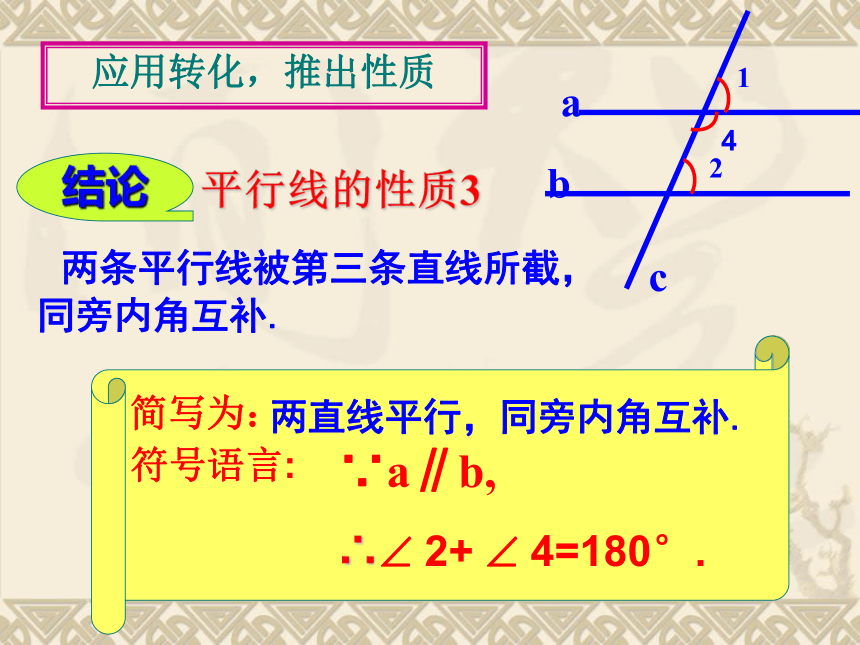
应用转化,推出性质
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
∴ 2+ 4=180°.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
4
应用转化,推出性质
两直线平行
判定
性质
已知
得到
得到
已知
说说平行线的“判定”与“性质”有什么不同
同位角相等
内错角相等
同旁内角互补
结束
类比发现,巩固性质
练一练:
如图,AB∥CD,AC∥BD,分别找出图中相等或互补的角。
C
A
B
D
1
2
3
4
学以致用,小试牛刀
如图所示,
(1)若DE∥BC,则可得到:
①∠1= ,根据 ;
②∠2= ,根据 ;
③∠4+ =1800,根据 .
(2)若EF∥AB,则可得到:
①∠1= ;
②∠B= ;
③∠2+ =1800.
∠B
两直线平行,同位角相等
∠5
两直线平行,内错角相等
∠B
两直线平行,同旁内角互补
∠2
∠5
∠4
学以致用,小试牛刀
如图,平行线AB、CD被直线AE所截.
(1)从∠1=1100,则可知道∠2= 度,
根据 ;
(2)从∠1=1100,则可知道∠3= 度,
根据 ;
(3)从∠1=1100,则可知道∠4= 度,
根据 .
110
两直线平行,内错角相等
110
两直线平行,同位角相等
70
两直线平行,同旁内角互补
学以致用,小试牛刀
1、下列说法:①两条直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行;④垂直于同一直线的两直线平行,其中是平行线的性质的是( )
A.① B.②和③ C.④ D.①和④
2、如图所示,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角(∠1除外)共有( )个
A.6个 B.5个 C.4个 D.3个
G
F
E
D
C
B
A
1
A
B
学以致用,小试牛刀
例题解析,深化理解
例1:如图,是一块梯形铁片的残余部分,量得∠A=100 ,∠B=115 ,梯形的另外两个角分别是多少度?
E
D
C
B
A
已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
求证 (1)DE和BC平行吗?为什么?
(2) ∠C是多少度?为什么?
拓展练习,综合应用
E
D
C
B
A
(已知)
(1)∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证)
∴∠AED=∠C
(两直线平行,同位角相等)
又∵∠AED=40°
(已知)
(等量代换)
∴∠C=40 °
2、已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
求证 (1)DE和BC平行吗?为什么?
(2) ∠C是多少度?为什么?
已知:如图,∠1=∠2,∠C=∠D,求证:∠A=∠F
证明:∵∠1=∠2( ),
∠2=∠3( )
∴∠1=∠__( )
∴BD∥CE( )
∴∠C=∠4( )
∵∠C=∠D( )
∴∠D=∠4( )
∴DF∥AC( )
∴∠A=∠F( )
3
2
B
A
C
D
E
F
1
4
3
同位角相等,两直线平行
两直线平行,同位角相等
已知
等量代换
内错角相等,两直线平行
两直线平行,内错角相等
已知
对顶角相等
等量代换
拓展练习,综合应用
已知:如图,∠AGD=∠ACB,∠1=∠2,CD与EF
平行吗?为什么?
拓展练习,综合应用
这节课,你最大的收获是什么?
探索的过程中你都运用了哪些方法?
你想给我们的学习伙伴哪些温馨提示呢?
知识梳理,归纳总结
新人教版义务教育教科书
七年级数学
5.3.1 平行线的性质
判定方法1 同位角相等,两直线平行.
判定方法2 内错角相等,两直线平行.
判定方法3 同旁内角互补,两直线平行.
梳理旧知,引出新课
结论
平行线的判定
两
直
线
平
行
梳理旧知,引出新课
条件
结论
?
两条平行线
被第三条直
线所截
梳理旧知,引出新课
条件
结论
同位角?
内错角?
同旁内角?
a
b
c
探究:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图中的一组同位角. 它们有怎样的数量关系?你是怎样得到的?
动手实践,归纳性质
两直线平行,同位角相等.
平行线的性质1
结论
两条平行线被第三条直线所截,
同位角相等.
∴∠1=∠2.
∵a∥b,
简写为:
符号语言:
b
1
2
a
c
动手实践,归纳性质
思考:
上一节,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”。类似地,你能出性质1,推出两条平行线被第三条直线截得的内错角之间的关系吗?
应用转化,推出性质
两直线平行,内错角相等.
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
∴∠2=∠3.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
3
应用转化,推出性质
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
∴ 2+ 4=180°.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
4
应用转化,推出性质
两直线平行
判定
性质
已知
得到
得到
已知
说说平行线的“判定”与“性质”有什么不同
同位角相等
内错角相等
同旁内角互补
结束
类比发现,巩固性质
练一练:
如图,AB∥CD,AC∥BD,分别找出图中相等或互补的角。
C
A
B
D
1
2
3
4
学以致用,小试牛刀
如图所示,
(1)若DE∥BC,则可得到:
①∠1= ,根据 ;
②∠2= ,根据 ;
③∠4+ =1800,根据 .
(2)若EF∥AB,则可得到:
①∠1= ;
②∠B= ;
③∠2+ =1800.
∠B
两直线平行,同位角相等
∠5
两直线平行,内错角相等
∠B
两直线平行,同旁内角互补
∠2
∠5
∠4
学以致用,小试牛刀
如图,平行线AB、CD被直线AE所截.
(1)从∠1=1100,则可知道∠2= 度,
根据 ;
(2)从∠1=1100,则可知道∠3= 度,
根据 ;
(3)从∠1=1100,则可知道∠4= 度,
根据 .
110
两直线平行,内错角相等
110
两直线平行,同位角相等
70
两直线平行,同旁内角互补
学以致用,小试牛刀
1、下列说法:①两条直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行;④垂直于同一直线的两直线平行,其中是平行线的性质的是( )
A.① B.②和③ C.④ D.①和④
2、如图所示,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角(∠1除外)共有( )个
A.6个 B.5个 C.4个 D.3个
G
F
E
D
C
B
A
1
A
B
学以致用,小试牛刀
例题解析,深化理解
例1:如图,是一块梯形铁片的残余部分,量得∠A=100 ,∠B=115 ,梯形的另外两个角分别是多少度?
E
D
C
B
A
已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
求证 (1)DE和BC平行吗?为什么?
(2) ∠C是多少度?为什么?
拓展练习,综合应用
E
D
C
B
A
(已知)
(1)∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证)
∴∠AED=∠C
(两直线平行,同位角相等)
又∵∠AED=40°
(已知)
(等量代换)
∴∠C=40 °
2、已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
求证 (1)DE和BC平行吗?为什么?
(2) ∠C是多少度?为什么?
已知:如图,∠1=∠2,∠C=∠D,求证:∠A=∠F
证明:∵∠1=∠2( ),
∠2=∠3( )
∴∠1=∠__( )
∴BD∥CE( )
∴∠C=∠4( )
∵∠C=∠D( )
∴∠D=∠4( )
∴DF∥AC( )
∴∠A=∠F( )
3
2
B
A
C
D
E
F
1
4
3
同位角相等,两直线平行
两直线平行,同位角相等
已知
等量代换
内错角相等,两直线平行
两直线平行,内错角相等
已知
对顶角相等
等量代换
拓展练习,综合应用
已知:如图,∠AGD=∠ACB,∠1=∠2,CD与EF
平行吗?为什么?
拓展练习,综合应用
这节课,你最大的收获是什么?
探索的过程中你都运用了哪些方法?
你想给我们的学习伙伴哪些温馨提示呢?
知识梳理,归纳总结
