人教版七年级数学下册 5.1.1相交线 课件(共18张PPT)
文档属性
| 名称 | 人教版七年级数学下册 5.1.1相交线 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 801.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
第五章 相交线与平行线
5.1 相交线
5.1.1 相交线
了解两条直线相交所构成的角,
理解并掌握对顶角、邻补角的概
念和性质。
1
2
学习目标
理解对顶角性质的推导过程,并会用这个性质进行简单的计算。
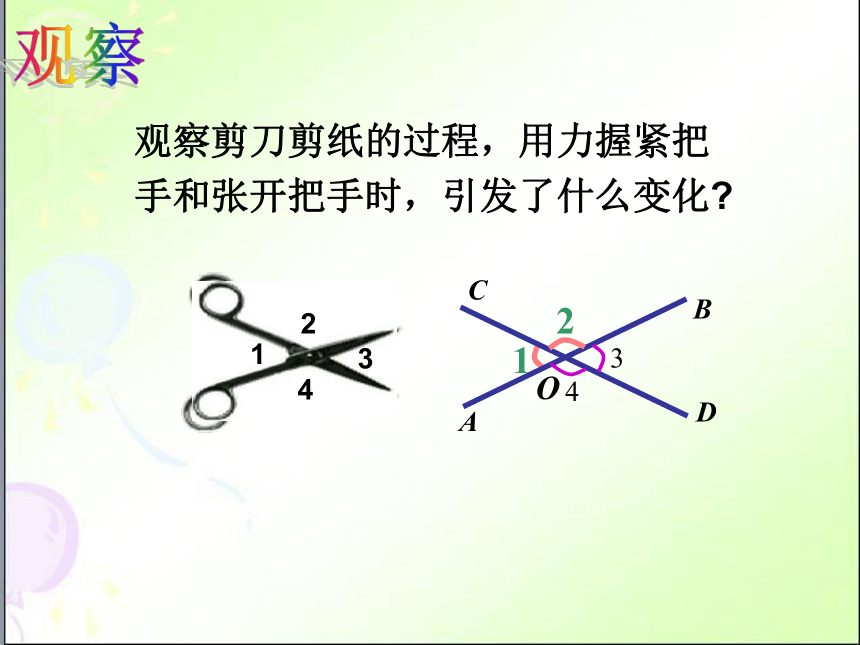
观察剪刀剪纸的过程,用力握紧把手和张开把手时,引发了什么变化
1
2
C
A
B
O
3
4
D
3
4
2
1
动手画出两条相交直线
1
2
3
4
B
A
C
D
o
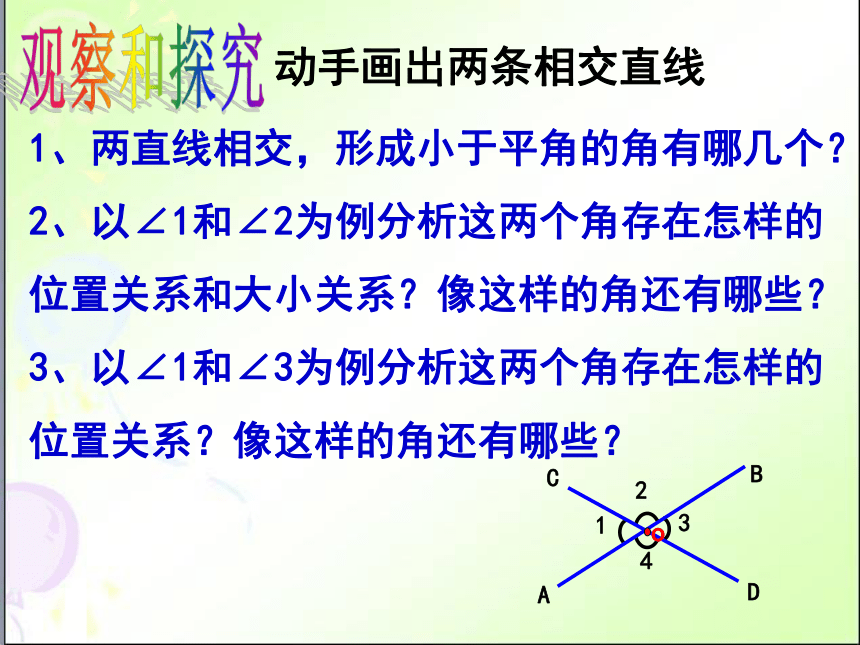
1、两直线相交,形成小于平角的角有哪几个?
2、以∠1和∠2为例分析这两个角存在怎样的位置关系和大小关系?像这样的角还有哪些?
3、以∠1和∠3为例分析这两个角存在怎样的位置关系?像这样的角还有哪些?
∠1,∠2,∠3,∠4
动手画出两条相交直线
1、两条直线相交,形成的小于平角的角
有哪几个?
1
2
3
4
B
A
C
D
o
1
2
3
4
B
C
D
o
A
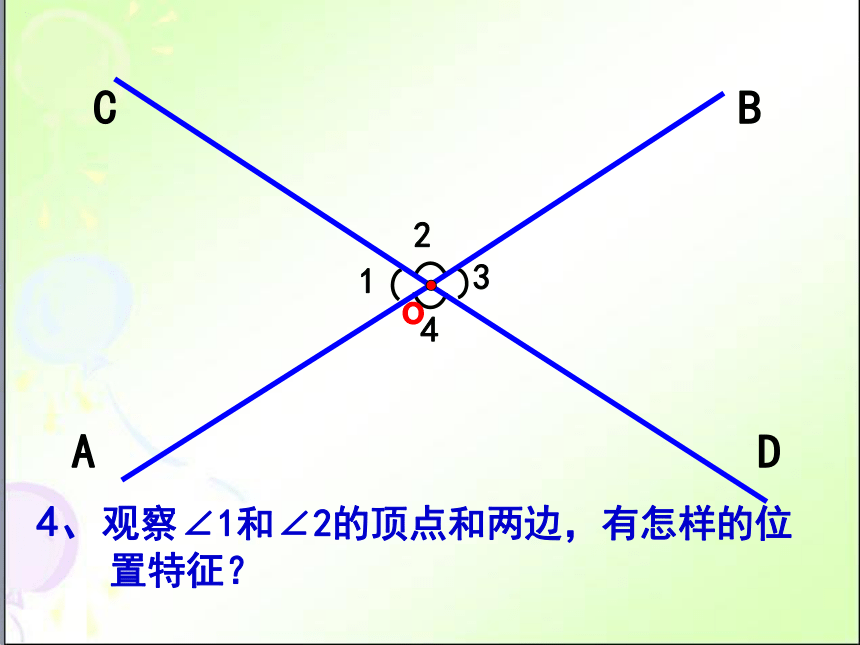
4、观察∠1和∠2的顶点和两边,有怎样的位
置特征?
1
3
B
C
D
A
2
4
o
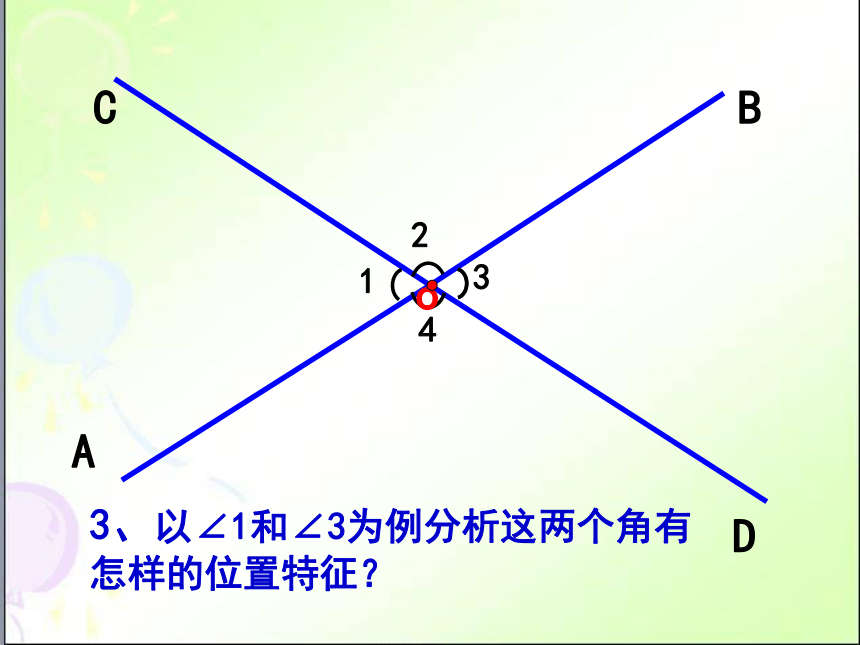
3、以∠1和∠3为例分析这两个角有
怎样的位置特征?
1.下列各图中∠1、∠2是邻补角吗?
为什么?
1
2
1
2
1
2
(1) (2) (3)
不是
不是
是
2.下列各图中∠1、∠2是对顶角吗?为什么?
1
2
1
2
2
1
(2)
(3)
(4)
(1)
不是
是
不是
不是
1
2
(5)
是
1
2
7、你能得到对顶角∠1和∠3的大小关系吗?
动动手:(1)、用量角器测量对顶角∠1和∠3,比较他们的大小 (2)将对顶角∠1和∠3进行翻折,比较它们的大小?
1
2
3
4
B
A
C
D
o
4、你能得到对顶角∠1和∠3的大小关系吗?
猜猜看:若直线CD绕点O转
动时,∠1和∠3 同
时缩小或增大,你
能猜出∠1和∠3的大小关系吗?
1
2
3
4
B
A
C
D
o
你能得到对顶角∠1和∠3的大小关系吗?
∠2与∠3互补,
∠1与∠2互补,
那么∠ 2 +∠1= ,
∠1= ∠3.
180°
180°
由同角的补角相等可知
动动脑:为什么?
∠ 2 +∠3= ,
1
2
3
4
B
A
C
D
o
对顶角的性质:
对顶角相等
例、如图,直线a、b相交,∠1=40°,求
∠2、∠3、∠4的度数。
a
b
)
(
1
3
4
2
)
(
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°
解:设∠1=x°,则∠2=3x°
变式2:若∠2是∠1的3倍,求∠3的度数?
根据邻补角的定义,得 x+3x=180
所以 x=45
根据对顶角相等,可得
∠3=∠1=45°
则∠1=45°
a
b
)
(
1
3
4
2
)
(
变式1:若∠1= 32°20′,求∠2、∠3、∠4的
度数。
今天我们学了什么?
邻补角、对顶角概念
邻补角、对顶角性质
分类
邻补角
两直线相交
对顶角
位置特征
大小特征
∠1+∠2=180°
∠2+∠3=180°
∠3+∠4=180°
∠4+∠1=180°
B
A
C
D
2
4
1
3
∠1=∠3
∠2=∠4
∠1 和∠2
∠2 和∠3
∠1 和∠3
∠3 和∠4
∠4 和∠1
∠2 和∠4
今天我们学了什么?
邻补角互补
对顶角相等
2、有一个______顶点,且其中一个角的两边分别是另一个角的两边的_________线的这样的两个角称作互为对顶角.
1、有一条______边,且它们的另一边互为_________线的这样的两个角称作互为邻补角.
公共
反向延长
反向延长
公共
课本P8第2题
课本P9第7题
第五章 相交线与平行线
5.1 相交线
5.1.1 相交线
了解两条直线相交所构成的角,
理解并掌握对顶角、邻补角的概
念和性质。
1
2
学习目标
理解对顶角性质的推导过程,并会用这个性质进行简单的计算。
观察剪刀剪纸的过程,用力握紧把手和张开把手时,引发了什么变化
1
2
C
A
B
O
3
4
D
3
4
2
1
动手画出两条相交直线
1
2
3
4
B
A
C
D
o
1、两直线相交,形成小于平角的角有哪几个?
2、以∠1和∠2为例分析这两个角存在怎样的位置关系和大小关系?像这样的角还有哪些?
3、以∠1和∠3为例分析这两个角存在怎样的位置关系?像这样的角还有哪些?
∠1,∠2,∠3,∠4
动手画出两条相交直线
1、两条直线相交,形成的小于平角的角
有哪几个?
1
2
3
4
B
A
C
D
o
1
2
3
4
B
C
D
o
A
4、观察∠1和∠2的顶点和两边,有怎样的位
置特征?
1
3
B
C
D
A
2
4
o
3、以∠1和∠3为例分析这两个角有
怎样的位置特征?
1.下列各图中∠1、∠2是邻补角吗?
为什么?
1
2
1
2
1
2
(1) (2) (3)
不是
不是
是
2.下列各图中∠1、∠2是对顶角吗?为什么?
1
2
1
2
2
1
(2)
(3)
(4)
(1)
不是
是
不是
不是
1
2
(5)
是
1
2
7、你能得到对顶角∠1和∠3的大小关系吗?
动动手:(1)、用量角器测量对顶角∠1和∠3,比较他们的大小 (2)将对顶角∠1和∠3进行翻折,比较它们的大小?
1
2
3
4
B
A
C
D
o
4、你能得到对顶角∠1和∠3的大小关系吗?
猜猜看:若直线CD绕点O转
动时,∠1和∠3 同
时缩小或增大,你
能猜出∠1和∠3的大小关系吗?
1
2
3
4
B
A
C
D
o
你能得到对顶角∠1和∠3的大小关系吗?
∠2与∠3互补,
∠1与∠2互补,
那么∠ 2 +∠1= ,
∠1= ∠3.
180°
180°
由同角的补角相等可知
动动脑:为什么?
∠ 2 +∠3= ,
1
2
3
4
B
A
C
D
o
对顶角的性质:
对顶角相等
例、如图,直线a、b相交,∠1=40°,求
∠2、∠3、∠4的度数。
a
b
)
(
1
3
4
2
)
(
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°
解:设∠1=x°,则∠2=3x°
变式2:若∠2是∠1的3倍,求∠3的度数?
根据邻补角的定义,得 x+3x=180
所以 x=45
根据对顶角相等,可得
∠3=∠1=45°
则∠1=45°
a
b
)
(
1
3
4
2
)
(
变式1:若∠1= 32°20′,求∠2、∠3、∠4的
度数。
今天我们学了什么?
邻补角、对顶角概念
邻补角、对顶角性质
分类
邻补角
两直线相交
对顶角
位置特征
大小特征
∠1+∠2=180°
∠2+∠3=180°
∠3+∠4=180°
∠4+∠1=180°
B
A
C
D
2
4
1
3
∠1=∠3
∠2=∠4
∠1 和∠2
∠2 和∠3
∠1 和∠3
∠3 和∠4
∠4 和∠1
∠2 和∠4
今天我们学了什么?
邻补角互补
对顶角相等
2、有一个______顶点,且其中一个角的两边分别是另一个角的两边的_________线的这样的两个角称作互为对顶角.
1、有一条______边,且它们的另一边互为_________线的这样的两个角称作互为邻补角.
公共
反向延长
反向延长
公共
课本P8第2题
课本P9第7题
