人教版七年级数学上册4.2.2 线段的性质 课件(共21张PPT)
文档属性
| 名称 | 人教版七年级数学上册4.2.2 线段的性质 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 934.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 13:27:48 | ||
图片预览



文档简介
(共21张PPT)
第四章 几何图形初步
4.2 直线、射线、线段
——线段的性质
人民教育出版社 数学 七年级 上册
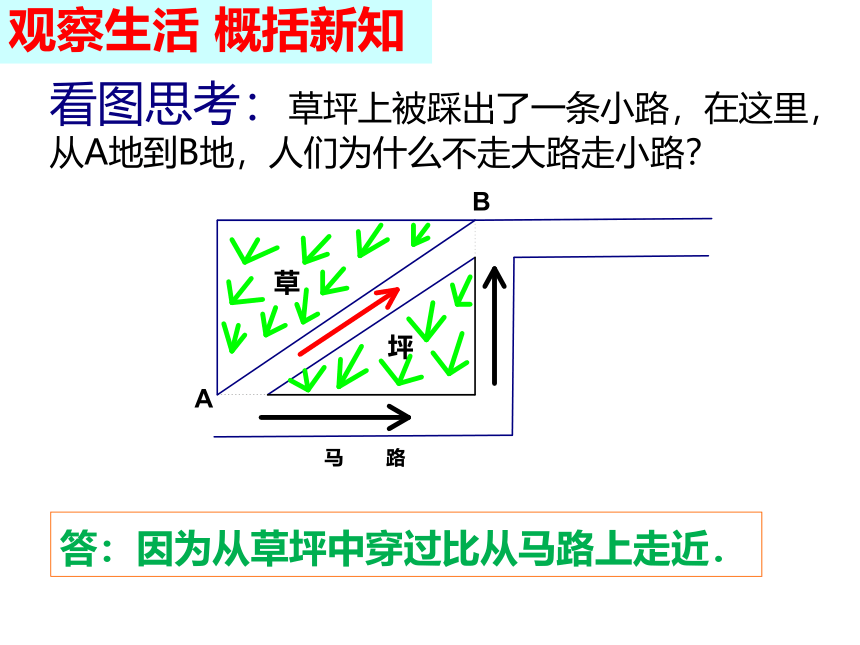
看图思考:草坪上被踩出了一条小路,在这里,从A地到B地,人们为什么不走大路走小路?
答:因为从草坪中穿过比从马路上走近.
观察生活 概括新知
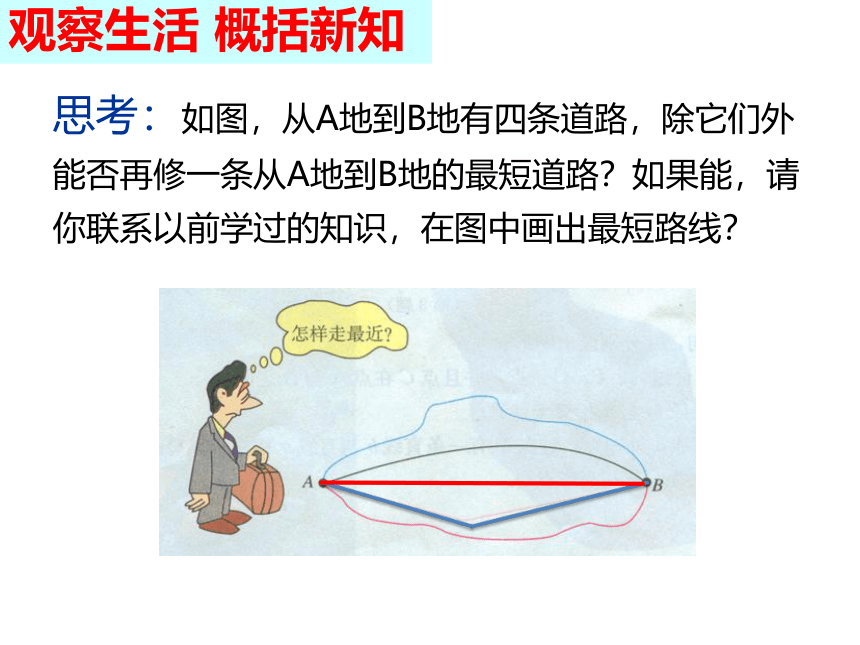
思考:如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你联系以前学过的知识,在图中画出最短路线?
观察生活 概括新知
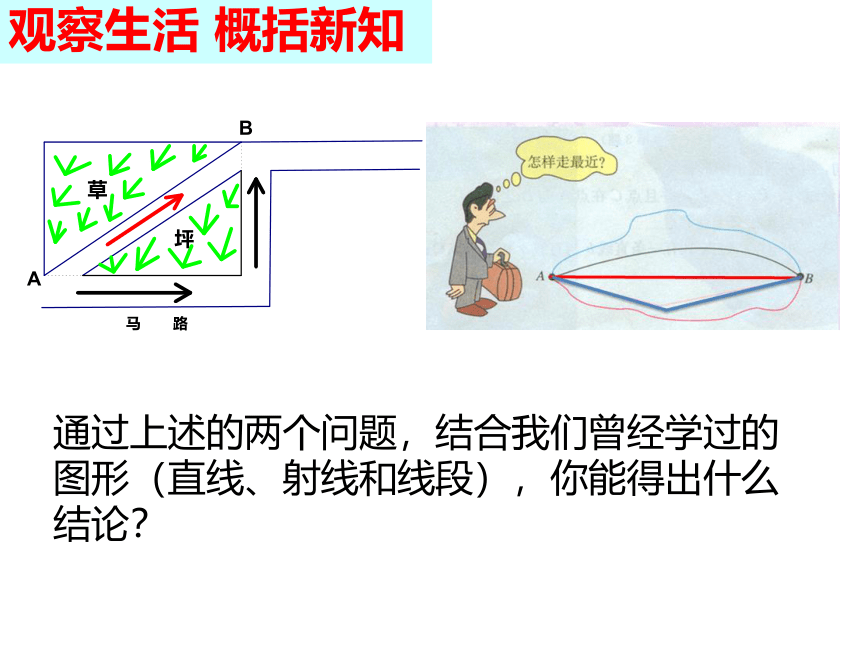
通过上述的两个问题,结合我们曾经学过的图形(直线、射线和线段),你能得出什么结论?
观察生活 概括新知
两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
连接两点间的线段的长度,叫做这两点的距离。
观察生活 概括新知
例1. 已知△ABC,AB、AC、BC分别表示三边的长.
(1)请问AB+AC与BC的大小关系如何?并说明理由.
解:(1)答:AB+AC﹥BC.
因为 两点之间线段最短,
所以 AB+AC﹥BC.
(2)仿照第(1)问,你能提出哪些问题?并解答提出的问题.
应用新知 解决问题
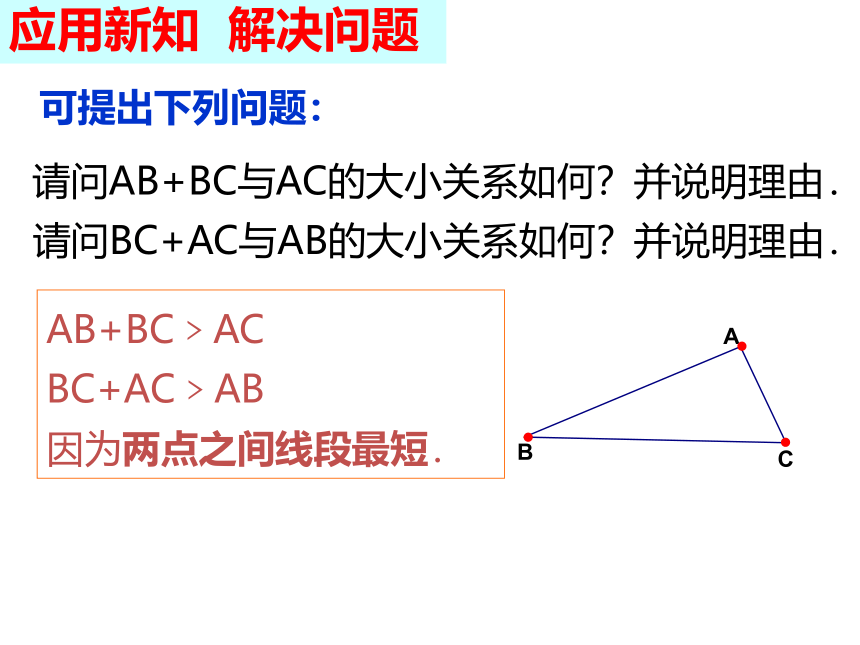
请问BC+AC与AB的大小关系如何?并说明理由.
请问AB+BC与AC的大小关系如何?并说明理由.
可提出下列问题:
AB+BC﹥AC
BC+AC﹥AB
因为两点之间线段最短.
应用新知 解决问题
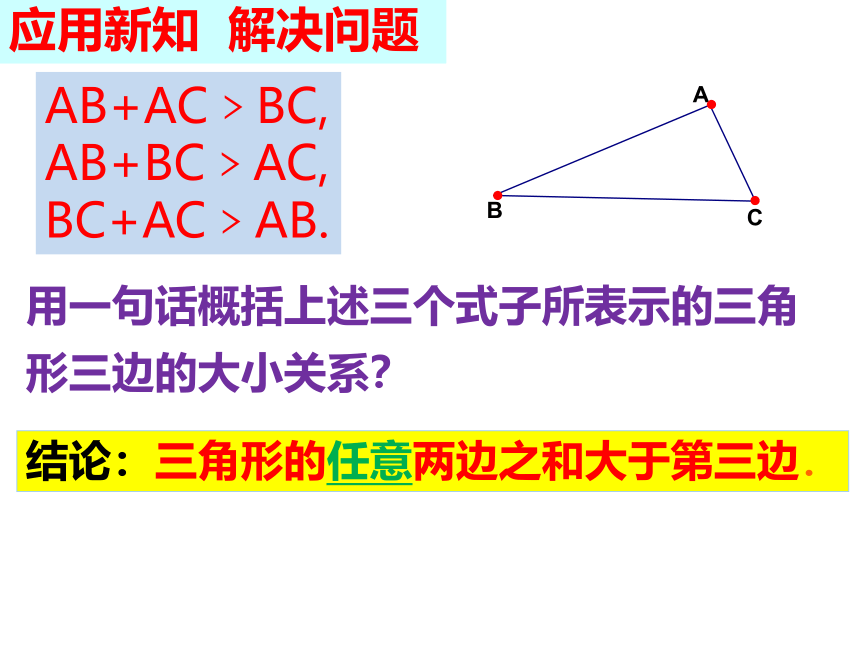
结论:三角形的任意两边之和大于第三边.
用一句话概括上述三个式子所表示的三角形三边的大小关系?
AB+AC﹥BC,
AB+BC﹥AC,
BC+AC﹥AB.
应用新知 解决问题
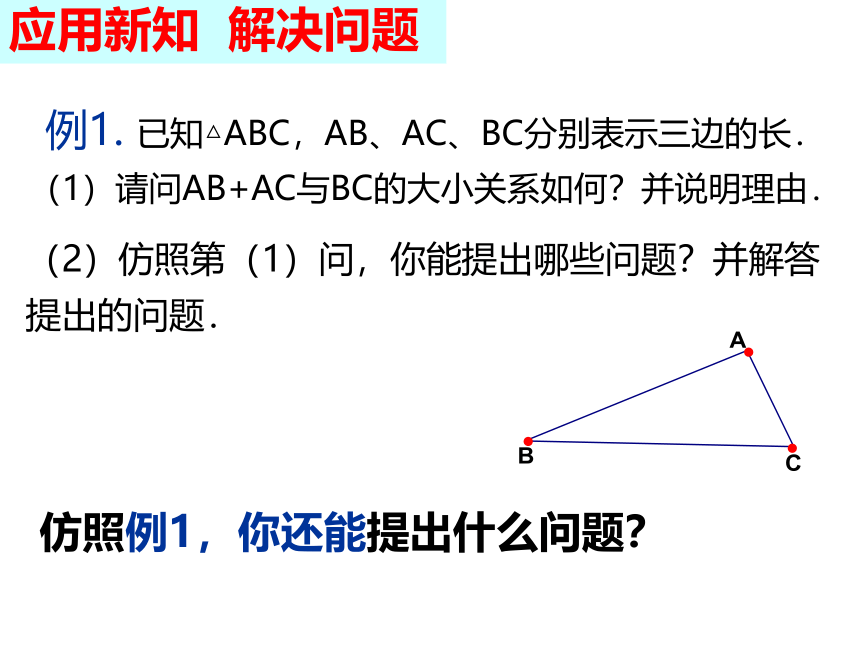
例1. 已知△ABC,AB、AC、BC分别表示三边的长.
(1)请问AB+AC与BC的大小关系如何?并说明理由.
(2)仿照第(1)问,你能提出哪些问题?并解答提出的问题.
应用新知 解决问题
仿照例1,你还能提出什么问题?
仿照例1,可提出如下问题:
1、已知四边形ABCD,AB、BC、CD、DA分别表示四边的长.
(1)请问AB+BC+CD与AD的大小关系如何?并说明理由.
解:AB+BC+CD﹥AD
(2)仿照第(1)问,你还能提出哪些问题?
结论:四边形的任意三边之和大于第四边.
用一句话概括上述关系式 中的规律?
应用新知 解决问题
2、已知五边形ABCDE……
……
三角形的任意两边之和大于第三边;
四边形的任意三边之和大于第四边;
五边形的任意四边之和大于第五边;
六边形的任意五边之和大于第六边;
……
结论:n边形任意n-1边之和大于第n边.
应用新知 解决问题
例2. 如图,马路m的北侧有个居民区A,南侧有另一个居民区B,公交车公司要在马路边修一个车站P,并且要使车站P到两个居民区A、B的距离和(PA+PB)最小.请确定车站P的位置(不考虑马路的宽度),并简述理由.
应用新知 解决问题
例3. 如图,马路m的北侧有两个居民区A、B,公交车公司要在马路边修一个车站P,并且要使车站P到两个居民区A、B的距离和(PA+PB)最小.请确定车站P的位置(不考虑马路的宽度),并简述理由.
应用新知 解决问题
学生做法一:
学生做法二:
画点关于直线的对称点,连接交直线m于点P.如图,点P即为所求的点.
正确做法:
连接线段AB并延长交直线m于点Q,连接
依据两点之间线段最短,有:;
因为点和点关于直线对称,所以
.
所以
应用新知 解决问题
方法1(点Q是线段AB延长线与直线m的交点)是错误的.
理由如下:
过点P做PQ⊥直线m,交直线m于点Q,连接QA.
依据两点之间线段最短,有:;
因为点和点关于直线对称,所以
.
所以
应用新知 解决问题
在直线m任取一点Q(P点除外),连接线段、和
依据两点之间线段最短,有:;
因为点和点关于直线对称,所以
.
所以
验证
应用新知 解决问题
1. 本节课你收获了哪些基本知识?
小结与评价
2. 通过本节课的学习,感悟到了哪些研究数学问题的方法?
3.请评价自己本节课的课堂表现;并请表扬一位同学,说说表扬他的理由;请给组内一名同学提一点建议.
课本:
130页 第8题必做;第11题选作.
三高练习册:
52页 第1~5题必做;第6~8题选作.
布置作业
第四章 几何图形初步
4.2 直线、射线、线段
——线段的性质
人民教育出版社 数学 七年级 上册
看图思考:草坪上被踩出了一条小路,在这里,从A地到B地,人们为什么不走大路走小路?
答:因为从草坪中穿过比从马路上走近.
观察生活 概括新知
思考:如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你联系以前学过的知识,在图中画出最短路线?
观察生活 概括新知
通过上述的两个问题,结合我们曾经学过的图形(直线、射线和线段),你能得出什么结论?
观察生活 概括新知
两点的所有连线中,线段最短.
简单说成:两点之间,线段最短.
连接两点间的线段的长度,叫做这两点的距离。
观察生活 概括新知
例1. 已知△ABC,AB、AC、BC分别表示三边的长.
(1)请问AB+AC与BC的大小关系如何?并说明理由.
解:(1)答:AB+AC﹥BC.
因为 两点之间线段最短,
所以 AB+AC﹥BC.
(2)仿照第(1)问,你能提出哪些问题?并解答提出的问题.
应用新知 解决问题
请问BC+AC与AB的大小关系如何?并说明理由.
请问AB+BC与AC的大小关系如何?并说明理由.
可提出下列问题:
AB+BC﹥AC
BC+AC﹥AB
因为两点之间线段最短.
应用新知 解决问题
结论:三角形的任意两边之和大于第三边.
用一句话概括上述三个式子所表示的三角形三边的大小关系?
AB+AC﹥BC,
AB+BC﹥AC,
BC+AC﹥AB.
应用新知 解决问题
例1. 已知△ABC,AB、AC、BC分别表示三边的长.
(1)请问AB+AC与BC的大小关系如何?并说明理由.
(2)仿照第(1)问,你能提出哪些问题?并解答提出的问题.
应用新知 解决问题
仿照例1,你还能提出什么问题?
仿照例1,可提出如下问题:
1、已知四边形ABCD,AB、BC、CD、DA分别表示四边的长.
(1)请问AB+BC+CD与AD的大小关系如何?并说明理由.
解:AB+BC+CD﹥AD
(2)仿照第(1)问,你还能提出哪些问题?
结论:四边形的任意三边之和大于第四边.
用一句话概括上述关系式 中的规律?
应用新知 解决问题
2、已知五边形ABCDE……
……
三角形的任意两边之和大于第三边;
四边形的任意三边之和大于第四边;
五边形的任意四边之和大于第五边;
六边形的任意五边之和大于第六边;
……
结论:n边形任意n-1边之和大于第n边.
应用新知 解决问题
例2. 如图,马路m的北侧有个居民区A,南侧有另一个居民区B,公交车公司要在马路边修一个车站P,并且要使车站P到两个居民区A、B的距离和(PA+PB)最小.请确定车站P的位置(不考虑马路的宽度),并简述理由.
应用新知 解决问题
例3. 如图,马路m的北侧有两个居民区A、B,公交车公司要在马路边修一个车站P,并且要使车站P到两个居民区A、B的距离和(PA+PB)最小.请确定车站P的位置(不考虑马路的宽度),并简述理由.
应用新知 解决问题
学生做法一:
学生做法二:
画点关于直线的对称点,连接交直线m于点P.如图,点P即为所求的点.
正确做法:
连接线段AB并延长交直线m于点Q,连接
依据两点之间线段最短,有:;
因为点和点关于直线对称,所以
.
所以
应用新知 解决问题
方法1(点Q是线段AB延长线与直线m的交点)是错误的.
理由如下:
过点P做PQ⊥直线m,交直线m于点Q,连接QA.
依据两点之间线段最短,有:;
因为点和点关于直线对称,所以
.
所以
应用新知 解决问题
在直线m任取一点Q(P点除外),连接线段、和
依据两点之间线段最短,有:;
因为点和点关于直线对称,所以
.
所以
验证
应用新知 解决问题
1. 本节课你收获了哪些基本知识?
小结与评价
2. 通过本节课的学习,感悟到了哪些研究数学问题的方法?
3.请评价自己本节课的课堂表现;并请表扬一位同学,说说表扬他的理由;请给组内一名同学提一点建议.
课本:
130页 第8题必做;第11题选作.
三高练习册:
52页 第1~5题必做;第6~8题选作.
布置作业
